数值分析答案第二章参数估计习题(精)

1．当1,1,2x =-时，()0,3,4f x =-,求()f x 的二次插值多项式。

解：0120121200102021101201220211,1,2,()0,()3,()4;()()1()(1)(2)()()2()()1()(1)(2)()()6()()1()(1)(1)()()3x x x f x f x f x x x x x l x x x x x x x x x x x l x x x x x x x x x x x l x x x x x x x ==-===-=--==-+-----==------==-+-- 则二次拉格朗日插值多项式为220()()k k k L x y l x ==∑0223()4()14(1)(2)(1)(1)23537623l x l x x x x x x x =-+=---+-+=+- 5设[]2(),f x Ca b ∈且()()0,f a f b ==求证： 21m ax ()()m ax ().8a x b a x bf x b a f x ≤≤≤≤''≤- 解：令01,x a x b ==，以此为插值节点，则线性插值多项式为10101010()()()x x x x L x f x f x x x x x --=+-- =()()x bx af a f b a b x a --=+--1()()0()0f a f b L x ==∴= 又 插值余项为1011()()()()()()2R x f x L x f x x x x x ''=-=--011()()()()2f x f x x x x x ''∴=--[]012012102()()1()()21()41()4x x x x x x x x x x b a --⎧⎫≤-+-⎨⎬⎩⎭=-=- 又 ∴21m ax ()()m ax ().8a x b a x bf x b a f x ≤≤≤≤''≤- 16．求一个次数不高于4次的多项式P （x ），使它满足(0)(0)0,(1)(1)0,(2)0P P P P P ''=====解：利用埃米尔特插值可得到次数不高于4的多项式0101010,10,10,1x x y y m m ======11300201001012()()()()(12)()(12)(1)j j j j j j H x y x m x x x x xx x x x x x x αβα===+--=---=+-∑∑210110102()(12)()(32)x x x x x x x x x x x α--=---=-2021()(1)()(1)x x x x x xββ=-=-22323()(32)(1)2H x x x x x x x ∴=-+-=-+设22301()()()()P x H x A x x x x =+--其中，A 为待定常数3222(2)1()2(1)P P x x x Ax x =∴=-++-14A ∴= 从而221()(3)4P x x x =-19．求4()f x x =在[,]a b 上分段埃尔米特插值，并估计误差。

数值分析习题（含答案）第一章绪论姓名学号班级习题主要考察点：有效数字的计算、计算方法的比较选择、误差和误差限的计算。

1 若误差限为5105.0-?,那么近似数0.003400有几位有效数字？（有效数字的计算）解：2*103400.0-?=x ，325*10211021---?=?≤-x x 故具有3位有效数字。

2 14159.3=π具有4位有效数字的近似值是多少？（有效数字的计算）解：10314159.0?= π，欲使其近似值*π具有4位有效数字，必需41*1021-?≤-ππ，3*310211021--?+≤≤?-πππ，即14209.314109.3*≤≤π即取（3.14109 , 3.14209）之间的任意数，都具有4位有效数字。

3 已知2031.1=a ，978.0=b 是经过四舍五入后得到的近似值，问b a +，b a ?有几位有效数字？（有效数字的计算）解：3*1021-?≤-aa ，2*1021-?≤-b b ，而1811.2=+b a ，1766.1=?b a 2123****102110211021)()(---?≤?+?≤-+-≤+-+b b a a b a b a故b a +至少具有2位有效数字。

2123*****10210065.01022031.1102978.0)()(---?≤=?+?≤-+-≤-b b a a a b ba ab 故b a ?至少具有2位有效数字。

4 设0>x ，x 的相对误差为δ，求x ln 的误差和相对误差？（误差的计算）解：已知δ=-**xx x ，则误差为δ=-=-***ln ln xx x x x则相对误差为******ln ln 1ln ln ln xxx x xxx x δ=-=-5测得某圆柱体高度h 的值为cm h 20*=，底面半径r 的值为cm r 5*=，已知cm h h 2.0||*≤-，cm r r 1.0||*≤-，求圆柱体体积h r v2π=的绝对误差限与相对误差限。

7、计算的近似值，取。

利用以下四种计算格式，试问哪一种算法误差最小。

〔1〕〔2〕〔3〕〔4〕解：计算各项的条件数由计算知，第一种算法误差最小。

解：在计算机上计算该级数的是一个收敛的级数。

因为随着的增大，会出现大数吃小数的现象。

9、通过分析浮点数集合F=〔10，3，-2，2〕在数轴上的分布讨论一般浮点数集的分布情况。

10、试导出计算积分的递推计算公式，用此递推公式计算积分的近似值并分析计算误差，计算取三位有效数字。

解：此算法是数值稳定的。

第二章习题解答1.〔1〕 R n×n中的子集“上三角阵〞和“正交矩阵〞对矩阵乘法是封闭的。

〔2〕R n×n中的子集“正交矩阵〞，“非奇异的对称阵〞和“单位上〔下〕三角阵〞对矩阵求逆是封闭的。

设A是ｎ×ｎ的正交矩阵。

证明A-1也是ｎ×ｎ的正交矩阵。

证明：〔2〕A是ｎ×ｎ的正交矩阵∴A A-1 =A-1A=E 故〔A-1〕-1=A∴A-1〔A-1〕-1=〔A-1〕-1A-1 =E 故A-1也是ｎ×ｎ的正交矩阵。

设A是非奇异的对称阵，证A-1也是非奇异的对称阵。

A非奇异∴A可逆且A-1非奇异又A T=A ∴〔A-1〕T=〔A T〕-1=A-1故A-1也是非奇异的对称阵设A是单位上〔下〕三角阵。

证A-1也是单位上〔下〕三角阵。

证明：A是单位上三角阵，故|A|=1，∴A可逆，即A-1存在，记为〔b ij〕n×n由A A-1 =E，那么〔其中 j＞i时，〕故b nn=1, b ni=0 (n≠j)类似可得，b ii=1 (j=1…n) b jk=0 (k＞j)即A-1是单位上三角阵综上所述可得。

R n×n中的子集“正交矩阵〞，“非奇异的对称阵〞和“单位上〔下〕三角阵〞对矩阵求逆是封闭的。

2、试求齐次线行方程组Ax=0的根底解系。

A=解：A=～～～故齐次线行方程组Ax=0的根底解系为，3.求以下矩阵的特征值和特征向量。

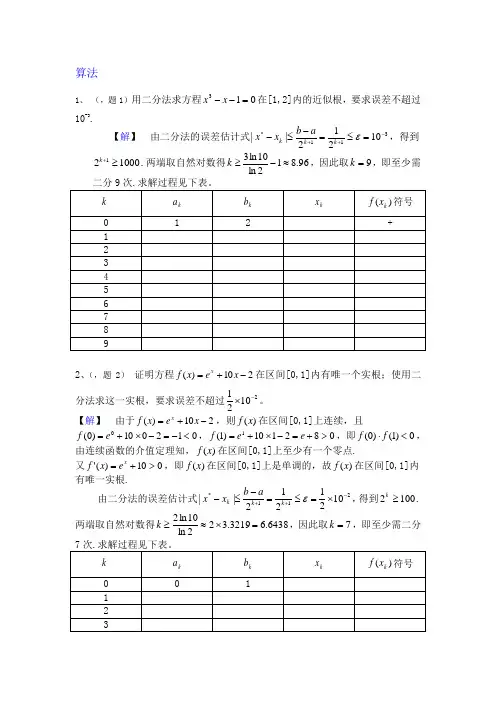
算法1、 （，题1）用二分法求方程013=--x x 在[1,2]内的近似根，要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ，得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ，因此取9=k ，即至少需2、（，题2） 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根；使用二分法求这一实根，要求误差不超过21021-⨯。

【解】 由于210)(-+=x e x f x ，则)(x f 在区间[0,1]上连续，且012010)0(0<-=-⨯+=e f ，082110)1(1>+=-⨯+=e e f ，即0)1()0(<⋅f f ，由连续函数的介值定理知，)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ，即)(x f 在区间[0,1]上是单调的，故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ，得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ，因此取7=k ，即至少需二分误差1．（，题8）已知e=…，试问其近似值7.21=x ，71.22=x ，x 2=，718.23=x 各有几位有效数字？并给出它们的相对误差限。

【解】有效数字：因为11102105.001828.0||-⨯=<=-K x e ，所以7.21=x 有两位有效数字； 因为12102105.000828.0||-⨯=<=-K x e ，所以71.22=x 亦有两位有效数字；因为3310210005.000028.0||-⨯=<=-K x e ，所以718.23=x 有四位有效数字；%85.17.205.0||111=<-=x x e r ε； %85.171.205.0||222=<-=x x e r ε； %0184.0718.20005.0||333=<-=x x e r ε。

第一章习题解答1. 在下列各对数中，X 是精确值ａ的近似值（1） ａ=π，x=3.1 （2） ａ=1/7，x=0.143 （3） ａ=π/1000，x=0.0031 （4） ａ=100/7，x=14.3 试估计x 的绝对误差和相对误差。

解：（1） e=∣3.1-π∣≈0.0416， δr = e/∣x ∣≈0.0143 （2） e=∣0.143-1/7∣≈0.0143 δr = e/∣x ∣≈0.1 （3） e=∣0.0031-π/1000∣≈0.0279 δr = e/∣x ∣≈0.9 (4) e=∣14.3-100/7∣≈0.0143 δr = e/∣x ∣≈0.0012. 已知四个数：x 1=26.3，x 2=0.0250， x 3= 134.25，x 4=0.001。

试估计各近似数的有效位数和误差限，并估计运算μ1= x 1 x 2 x 3和μ1= x 3 x 4 /x 1的相对误差限。

解：x 1=26.3 ｎ=3 δx 1=0.05 δr x 1=δx 1/∣x 1∣=0.19011×10-2x 2=0.0250 ｎ=3 δx 2=0.00005 δr x 2=δx 2/∣x 2∣=0.2×10-2x 3= 134.25 ｎ=5 δx 3=0.005 δr x 3=δx 3/∣x 3∣=0.372×10-4x 4=0.001 ｎ=1 δx 4=0.0005 δr x 4=δx 4/∣x 4∣=0.5由公式：e r （μ）= e （μ）/∣μ∣≦1/∣μ∣Σni=1∣∂f/∂x i ∣δx ie r （μ1）≦1/∣μ1∣［x 2 x 3δx 1+ x 1 x 3δx 2 +x 1x 2δx 3］ =0.34468/88.269275 =0.0039049e r （μ2）≦1/∣μ2∣［-x 3 x 4/ x 21δx 1+ x 4/ x 1δx 3 + x 3/ x 1δx 4］ =0.497073. 设精确数ａ>0，x 是ａ的近似值，x 的相对误差限是0.2，求㏑x 的相对误差限。

第一章 绪论（12） 第二章 插值法（40-42）2、当2,1,1-=x 时，4,3,0)(-=x f ，求)(x f 的二次插值多项式。

[解]372365)1(34)23(21)12)(12()1)(1(4)21)(11()2)(1()3()21)(11()2)(1(0))(())(())(())(())(())(()(2221202102210120120102102-+=-++--=+-+-⨯+------⨯-+-+-+⨯=----+----+----=x x x x x x x x x x x x x x x x x x x y x x x x x x x x y x x x x x x x x y x L 。

3、给出x x f ln )(=的数值表用线性插值及二次插值计算54.0ln 的近似值。

X 0.4 0.5 0.6 0.7 0.8 x ln -0.916291 -0.693147 -0.510826 -0.357765 -0.223144[解]若取5.00=x ，6.01=x ，则693147.0)5.0()(00-===f x f y ，510826.0)6.0()(11-===f x f y ，则604752.182321.1)5.0(10826.5)6.0(93147.65.06.05.0510826.06.05.06.0693147.0)(010110101-=---=--⨯---⨯-=--+--=x x x x x x x x x y x x x x y x L ，从而6202186.0604752.19845334.0604752.154.082321.1)54.0(1-=-=-⨯=L 。

若取4.00=x ，5.01=x ，6.02=x ，则916291.0)4.0()(00-===f x f y ，693147.0)5.0()(11-===f x f y ，510826.0)6.0()(22-===f x f y ，则 217097.2068475.404115.2)2.09.0(5413.25)24.0(3147.69)3.01.1(81455.45)5.06.0)(4.06.0()5.0)(4.0()510826.0()6.05.0)(4.05.0()6.0)(4.0()693147.0()6.04.0)(5.04.0()6.0)(5.0(916291.0))(())(())(())(())(())(()(22221202102210120120102102-+-=+--+-⨯++-⨯-=----⨯-+----⨯-+----⨯-=----+----+----=x x x x x x x x x x x x x x x x x x x x x x y x x x x x x x x y x x x x x x x x y x L ，从而61531984.0217097.21969765.259519934.0217097.254.0068475.454.004115.2)54.0(22-=-+-=-⨯+⨯-=L补充题：1、令00=x ，11=x ，写出x e x y -=)(的一次插值多项式)(1x L ，并估计插值余项。

《数值分析》练习题及答案解析第一章 绪论主要考查点：有效数字，相对误差、绝对误差定义及关系；误差分类；误差控制的基本原则；。

1. 3.142和3.141分别作为π的近似数具有（ ）和（ ）位有效数字.A ．4和3B ．3和2C ．3和4D ．4和4 答案：A2. 设 2.3149541...x *=，取5位有效数字，则所得的近似值x=___________ .答案：2.31503.若近似数2*103400.0-⨯=x 的绝对误差限为5105.0-⨯,那么近似数有几位有效数字 解：2*103400.0-⨯=x ，325*10211021---⨯=⨯≤-x x 故具有3位有效数字。

4 . 14159.3=π具有4位有效数字的近似值是多少？解：10314159.0⨯= π，欲使其近似值*π具有4位有效数字，必需！41*1021-⨯≤-ππ，3*310211021--⨯+≤≤⨯-πππ，即14209.314109.3*≤≤π即取（ , ）之间的任意数，都具有4位有效数字。

第二章 非线性方程求根 主要考查点：二分法N 步后根所在的区间，及给定精度下二分的次数计算；非线性方程一般迭代格式的构造，（局部）收敛性的判断，迭代次数计算； 牛顿迭代格式构造；求收敛阶；1.用二分法求方程012=--x x 的正根，要求误差小于0.05。

（二分法）解：1)(2--=x x x f ，01)0(<-=f ，01)2(>=f ，)(x f 在[0，2]连续，故[0，2]为函数的有根区间。

"（1）计算01)1(<-=f ，故有根区间为[1，2]。

（2）计算041123)23()23(2<-=--=f ，故有根区间为]2,23[。

（3）计算0165147)47()47(2>=--=f ，故有根区间为]47,23[。

（4）计算06411813)813()813(2>=--=f ，故有根区间为]813,23[。

第二章习题参考答案1.解： 由于20Ax b−≥，极小化2b Ax −与极小化22Ax b −是等价的。

令22()(,)(,)2(,)x Ax b Ax Ax b b Ax b ϕ=−=+−，对于任意的n R y x ∈,和实数α，)()(),()()(,*222*2****x Ay a x Ay Ay a x ay x b Ax x ϕϕϕϕ≥+=+=+=则有满足若这表示处达到极小值。

在*)(x x ϕ反之，若必有处达到极小，则对任意在nR y x ay x ∈+*)(ϕ0),(2),(2),(20)(**0*=−=+−=+=Ay b Ax Ay Ay a Ay b Ax daay x d a 即ϕ故有 b Ax =*成立。

以上证明了求解,22b Ax b Ax −=等价于极小化即。

等价于极小化2b Ax b Ax −= 推导最速下降法过程如下：),/(),(0),(),(,0),,2)(222)()(11k T k T k T k k T k T k T k k T k k k T k k kT k T k T T x x k r AA r AA r AA r a r AA r AA a r AA r r aA x da dx a r aA x x r A Ax b A Ax A b A x grad x x k==+−=++==−=−=−++=最终得到得出（由取得极小值。

使求出取的负梯度方向，且下降最快的方向是该点在ϕϕϕ给出的算法如下：1）)(000Ax b A r A R x T T n −=∈，计算给定； 2）L ,2,1,0=k 对于）转到否则数。

为一事先给定的停机常则停止；其中若2),/(),(10,11kT k k k k T k k k k k k k k k r A p Ax b r r A a x x Ap Ap p p a k k r =−=+==+=>≤−−εε2.证明 1） 正定性由对称正定矩阵的性质，(),0x Ax ≥（当且仅当x ＝0时取等号），所以 ()12,0Axx Ax =≥（当且仅当x ＝0时取等号）2） 齐次性()()()121122,(),,AA xx A x x Ax x Ax x αααααα⎡⎤====⎣⎦3）o1方法（一）A 是对称正定矩阵，得到(,())0x y A x y λλ++≥，把它展开如下2(,)(,)(,)(,)0y Ay x Ay y Ax x Ax λλλ+++≥考虑到(,)(,)(,)x Ay Ax y y Ax ==，把上式看成关于λ的一元二次方程，则式子等价于24(,)4(,)(,)0x Ay x Ax y Ay ∆=−≤因此1/21/2(,)(,)(,)x Ay x Ax y Ay ≤所以1/21/221/21/2((,)(,))(,)(,)2(,)(,)(,)(,)2(,)(,)(,)(,)(,)((),())x Ax y Ay x Ax y Ay x Ax y Ay x Ax y Ay x Ay x Ax y Ay x Ay y Ax x y A x y +=++≥++=+++=++两边开平方即可得到AA A x yx y +≤+因此，1/2(,)A x Ax x =是一种向量范数。

第二章插值法1.当兀= 1—2时,/（%） = 0-3,4^/（%）的二次插值多项式。

解：X。

= I/】=—l,x2 = 2, /Uo) =0,/(^)=-3,/(X2) = 4;一丄(兀+i)(一2)，0（人）=Oo — xJOo — xJ 2加）=（_兀）（—心=丄（一1）（一2）（兀一兀）（州一呂）6(A-.VoX.V-Vj l(Y_1)(x+1)(x2-x Q)(x2-x t) 3则二次拉格朗口插值多项式为2厶⑴=£）恥）k=0=-3/0(X)+4/2(X)1 4= --U- 1)(A—2) + -(x-l)(x + 1)5r 3 7=-X" +—x--6 2 3/（x） = liix2.用线性插值及二次插值计算1110.54的近似值。

解：由表格知，x0 = 0・4，兀=0.59X2 = 0.6, x3 = 0.7,x4 = 0.8; f(x Q) = -0.916291,/(xj = -0.693147 /(A) = —0.510826,/a)= -0.356675 /(x4) =-0.223144若采用线性插值法计算hiO.54即/(0.54),则0.5 <0.54 <0.6/1(x) = ^—^ = -10(.v-0.6) 人一无X —X /.(%) = -__ =-10(x-0.5)厶⑴=/U1XW + /(x 2)/2(x)=6.93147(x — 0.6) - 5・ 10826(.— 0.5)・・・厶(0.54) = -0.6202186 « -0.620219若采用二次插值法计算lnO.54时, (V f _亠)=50(x-0.5)(x- 0.6)(x Q -xj(x 0-x 2)(工7。

)(工_亠)=-100(x- 0.4)(x — 0.6)(兀一 Xo )(X 】一XJ厶(x) = /UoVoW+/U1XW+/(x 2)/2(x )=-50 x 0.916291(%-0.5)(A -0.6)+ 69.3147(x-0.4)(x-0.6)-0.510826 x50(x-0.4)(x-0.5).14(0.54) = -0.61531984 « -0.615320 3.给全cosx,0 <x<90°的函数表,步长/? = r = （l/60）\若函数表具有5位有效数字，研 究用线性插值求cos 兀近似值时的总误差界。

1、设函数()f x 的导数满足'0()m f x M <≤≤，且0)(=x f 的根存在，x 任意，证明：任取2(0,)Mλ∈，迭代格式 1()k k k x x f x λ+=-对任意初值0x 均收敛于0)(=x f 的根*x 。

证明：由题意可取定义域为R 。

由于0)('>x f ，0)('>x f 为单调函数，又0)(=x f 的根存在，所以方程0)(=x f 的根*x 是唯一的。

由迭代格式1()k k k x x f x λ+=-可以得到迭代函数)()(x f x x λϕ-=且|)('1||)('|x f x λϕ-=又'0()m f x M <≤≤及M20<<λ得 2)('0<≤≤<M x f m λλλ所以有 11)('111<-≤-≤-<-m x f M λλλ 故 1|}1||,1max{||)('|<--=≤M m L x λλϕ 此外，显然有()x R x R ϕ∀∈⇒∈由定理知迭代)()(111---=-=k k k k x x f x x ϕλ对任意初值0x 均收敛于0)(=x f 的根*x 。

2.提示：()22cos 2133x x ϕ'=≤<3.取迭代函数()[1,2]x x ϕ=∈讨论之。

4.由101kk L x p x x L-≤--确定k,迭代次数59.5.迭代公式及区间为()[]11,1.5,2x x ϕ=+。

7、2cos 2x x =≤，可以界定根的范围，用Newton 迭代公式及定理2-6做；8.三个根：[]()21,0,,*0.45896x x e x ϕ-=≈- ；[]()20,1,,*0.9100x x e x ϕ=≈9.取()n f x x a =-，当0a >时，取区间[0,1]a +，用定理6做，当0a <时，由()1n=-11提示：因为()()2233x x a x x aϕ+=+用定理2.4)33a a a aϕ+==+()()()()()()()()()()22222223333633361331101x x a x x a x x x a x ax x x a x x ax x x x a ϕϕϕϕϕϕϕ+=⇔+=++'++=+'⇒=-+'⇒==-=<收敛，由(3123kk kx x x a+=+可得12.()()()()()()()()()()()()()()()()()222******1*22*****1*2***2*3(),()2'()2!()'()'()2'()'()'()2()'()2k k kk k k kk k k k k k k kkk k k kkk f f y x x x f y f x f x y x y x f x f x f f y x x y x y x y x y x f x f x f x y x f f x f x y x f x y x f x x f f x ξξξξξξ+'''''-=-=+-+-'''∴-=--=------''⎛⎫'=--- ⎪⎝⎭-''''=-+ ()()()()()2*13*121*32()2'()()()()4'()2'()k k k k k k f x x f x x x f f f f x x f x f x ξξξξξ⎛⎫''⨯- ⎪⎝⎭''-''''⎛⎫''=+- ⎪⎝⎭()2**13**1()lim2'()k k kx x f x f x xx+→∞''⎛⎫-= ⎪⎝⎭- 13.提示：借助()()()()**,0mf x x xg x g x =-≠代入*1k xx +-中约化。

习题21. 分析下列方程各存在几个根，并找出每个根的含根区间：(1) 0cos =+x x ； (2) 0cos 3=-x x ； (3) 0sin =--x e x ； (4) 02=--x e x 。

解：(1) 0cos =+x x (A) x x x f cos )(+= ，0sin1)(≥-='x x f ,),(∞-∞∈x10cos 0)0(=+=f ,01cos 1)1cos(1)1(<+-=-+-=-f ∴ 方程(A) 有唯一根 ]0,1[*-∈x (2) 0cos 3=-x x (B) x x x f c o s 3)(-=,0sin 3)(>+='x x f , ),(∞-∞∈x 时010c o s03)0(<-=-⨯=f ，01cos 31cos 13)1(>-=-⨯=f ∴ 方程(B) 有唯一根 ]1,0[*∈x (3)sin =--xex (C)xex -=sinx x f sin )(1=, xex f -=)(2方程(C)有无穷个正根，无负根 在[22,2πππ+k k ] 内有一根 )(1k x ，且0]2[lim )(1=-∞→πk x k k在[ππππ++k k 2,22]内有一根)(2k x ，且0])12([lim )(2=+-∞→πk x k k (示图如下) 3,2,1,0=k)(2x f x(4)02=--xex(D) xex-=2,)(21x x f = xex f -=)(2方程(D) 有唯一根 ]1,0[*∈x 当 0<x 时 (D)与方程2x ex -=- (E) 同解 当 0<x 时 (E)无根 2. 给定方程 012=--x x ； (1)(2)若在[0 , 2]上用二分法求根，要使精确度达到6位有效数，需二分几次？ 解：012=--x x1) 01)(2=--=x x x f 1)1(-=f , 025.0)5.1(<-=f ,1)2(=f]2,5.1[*∈x, 618034.1251*=+=x)(5.1- 1.75(+) 2(+) )(5.1- 1.625(+) 1.75(+) )(5.1-1.5625(+) 1.625(+))(5625.1- )(59375.1-1.625(+)1102103125.02)5625.1625.1(-⨯<=-6.159375.1*≈≈x2位有效近似值为 1.6 2)00==a a ， 20==b b)(21k k k b a c +=kk k a b c x 2121*=-≤-+5102121-⨯≤k，51102≥-k60.162ln 10ln 51=≥-k∴ 只要2等分18次3. 为求0353=--x x 的正根，试构造3种简单迭代格式，判断它们是否收敛，且选择一种较快的迭代格式求出具有3位有效数的近似根。

第二章习 题 解 答西南交大 草上飞1下列数据作为π=*x 的近似数,试确定它们各有几位有效数字,并确定其相对误差限..722,15.3,14.3,141.34321====x x x x (i x 表示*x 的近似数,)1415926.3 =π 解：把近似数)4,3,2,1(*=i x i 规格化形式后均有1=k ，首位非零数字为3Ⅰ）31*11021005.000059.0141.3-⨯=≤=-=- πx x *1x 有3位有效数字，0017.010321)(31*1≈⨯⨯=-x r ε Ⅱ) 31*21021005.0001.014.3-⨯=≤=-=- πx x*2x 有3位有效数字，0017.010321)(31*2≈⨯⨯=-x r ε Ⅲ) 21*31021005.0008.015.3-⨯=≤=-=- πx x*3x 有2位有效数字，017.010321)(21*3≈⨯⨯=-x r ε Ⅳ)142857.3722=， 31*41021005.0001.0722-⨯=≤=-=- πx x *4x 有3位有效数字，0017.010321)(31*4≈⨯⨯=-x r ε 2 证明§2.2中的定理 2.1,定理 2.2.3 已知20的近似数x 相对误差为%5.0，试问x 至少有几位有效数字？解：因20的第一位数字为4，所以x 的第一位数字41=a ，根据定理2.1，当n r a x e -⨯+≤1015|)(|1 成立时，x 有n 位有效数字，而2=n 时,101451019510005%5.0)(22--⨯+<⨯+===x e r 所以近似数x 至少有2位有效数字.4 为尽量避免有效数字的严重损失，当1||<<x 时应如何加工下列计算公式：（1）xx x +--+11211 （2）x cos 1- （3）1-xe解：（1）)1)(21(22x x x ++；（2）2sin 22x ；（3）4322416121x x x x +++ 5 序列{}n y 满足递推关系()⎪⎩⎪⎨⎧=-==- ,2,1,110210n y y y n n若取41.120≈=y 做近似计算，问计算到10y 时误差有多大？这个计算过程稳定吗？解：,414.120 ==y ,41.1*=y δ=⨯≤--2*001021||y y 10||*11=-y y δ10||*00≤-y y10||*1010=-y y δ10*0010*9910||10||≤-==-y y y y 此递推关系每计算一次误差增长10倍，故算法不稳定. 6设,,1,0,11 ==⎰-n dx e x I x n n 验证,110--=e I .11--=n n nI I 若取,3679.01≈-e 依次计算 n I I I ,,10时(不要求具体算出),请你证明这样设计的算法其误差传播是逐步扩大的,算法是不稳定的.并要求另外设计一种数值稳定的算法.解: ,11110⎰---==e dx eI x 对n I 用分部积分法得==⎰-11dx e x I x n n ⎰-11x n de x ne x x n -=-101|⎰--111dx e x x n .11--=n nI设误差,*n n n I I e -=其中*1*1--=n n nI I .于是=--=-=--)(*11*n n n n n I I n I I e =--=)(!)1(*00I I n n 0!)1(e n n - 当n 增大时n e 是递增的, *n I 的误差达到0!)1(e n n -,是严重失真的.数值稳定的计算方法: 将递推公式11--=n n nI I 改为)1(11n n I nI -=- )1,2,1,( -=k k n 于是在从后往前计算时, 1-n I 的误差减少为原来n I 的n1,若取k n =足够大,误差逐步减少,计算结果是稳定可靠的. 7 7可由下列迭代公式计算:⎪⎩⎪⎨⎧=+==+,2,1,0),7(21210k x x x x k k k若k x 是7的具有n 位有效数字的近似值,求证1+k x 是7的具有n 2位有效数字的近似值.解 由1+k x ,1,0,)7(217)7(2172=-=-+=-k x x x x k kk k 和20=x ,得到,,2,1,7 =≥k x k 数列∞=1}{k k x 有下界.又1)11(21)71(2121=+≤+=+kk k x x x 即k k x x ≤+1,数列∞=1}{k k x 单调不增. 故k k x ∞→lim 存在.令∞→k ,对迭代公式两边取极限,可求得7lim =∞→k k x .现设k x 是7的具有n 位有效数字的近似值,即有11021|7|+-⨯≤-n k x 于是,得|7|1-+k x 2)7(721-≤k x 221041721+-⨯⨯≤n 121021+-⨯≤n可见, 1+k x 是7的具有n 2位有效数字的近似值.8用秦九韶算法计算多项式4532)(23-+-=x x x x p 在自变量3=x 时的值. 解：381432429634532-- 故 38)3(=p补充例题例题1：试问真值62.2*=x 的近似数 2.58x =是否为有效数. 解：*112110.040.05101022x x ---=<=⨯=⨯∴由有效数的定义知近似数 2.58x =具有两位有效数字，分别是2,5由于8不是有效数字，故 2.58x =不是有效数.例题2为尽量避免有效数字的严重损失，当1||>>x 时应如何加工下列计算公式xx x x 11--+解： 为尽量避免有效数字的严重损失，应作变换：xx x x x xx x x 11211-++=--+例题3 设10000,2,1,0,1==⎰n dx e x I x n n（1）证明：.10000,,3,2,1,1 =-=-n nI e I n n （2）设计一种数值稳定的算法，并证明算法的稳定性. 解: (1) 对n I 用分部积分法得 ==⎰1dx e x I x n n ⎰1x n de x n e x x n -=10|⎰-11dx e x x n.10000,,3,2,1,1101 =-=-=--⎰n nI e dx e x n e n x n(2) 由（1）得：,1n n I e nI -=-若已知N I ，设计如下递推算法： 1,2,1,),(11 --=-=-N N N n I e nI n n 注意到： )1,0(,1|110110∈+=+==+⎰ξξξξn e n x e dx x e I n nn ,于是.111+<<+n e I n n 取)1(21++=N eI N 可得如下递推算法1,2,,1,,)1(21)(11 -=⎪⎪⎩⎪⎪⎨⎧++=-=-N N n N e I I e n I N n n . 设 n n n I I e -=，则11---n n I I )(1n n I I n--=， ||11---n n I I |)(|1n n I I n -=，即n n e ne 11=-.每迭代一次误差均在减少，所以设计的递推算法是数值稳定的.例题4 已知,1410⎰+=dx x x y nn 试建立一个具有较好数值稳定性的求),2,1( =n y n 的递推公式,并证明算法的稳定性.解: 由=+-14n n y y ⎰++-101144dx x x x n n =n dx x n 1101=⎰- 得到求),2,1( =n y n 的递推公式:14141--=n n y n y , ,2,1=n (*) 而初值40235.0|)]14[ln(4114110100≈+=+=⎰x dx x y ,由此出发,根据上述递推公式可以求 ),2,1( =n y n 的近似值求*ny : *1*4141--=n n y n y , ,2,1=n . 记*n y 的绝对误差为||*n n n y y -=∆,则有:)(41*11*----=-n n n n y y y y ,即141-∆=∆n n , ,2,1=n . 由此可见,*1-n y 的误差将缩小41传播到*n y ,误差传播是逐步衰减的.因而,递推公式(*)是数值稳定的.例题5 数列{}n x 满足递推公式1101(1,2,)n n x x n -=-=.若取*001.41(3x x =≈=位有有效数字),问按此递推算法从0x 算至10x 时误差有多大?这个计算过程稳定吗? 解: *20001||||102e x x ε-=-=<⨯ *00||||10||10n nn n n n e x x x x ε=-=-=,||()n e n →∞→∞,则计算过程不稳定.计算至10x 时误差: 10281011||10101022e -=⨯⨯=⨯.。

数值分析作业第二章1、用Gauss消元法求解下列方程组：2x1-x2+3x3=1,(1) 4x1+2x2+5x3=4,x1+2x2=7;(2) 解：A=[2 -1 3 1;4 2 5 4;1 2 0 7]n=size(A,1);x=zeros(n,1);flag=1;% 消元过程for k=1:n-1for i=k+1:nif abs(A(k,k))>epsA(i,k+1:n+1)=A(i,k+1:n+1)-A(k,k+1:n+1)*A(i,k)/A(k,k); elseflag=0;returnendendend% 回代过程if abs(A(n,n))>epsx(n)=A(n,n+1)/A(n,n);elseflag=0;returnendfor i=n-1:-1:1x(i)=(A(i,n+1)-A(i,i+1:n)*x(i+1:n))/A(i,i); endreturnxA = 2 -1 3 14 25 41 2 0 7x = 9-1-611x1-3x2-2x3=3,(2)-23x1+11x2+1x3=0,x1+2x2+2x3=-1;(2) 解：A=[11 -3 -2 3;-23 11 1 0;1 2 2 -1]n=size(A,1);x=zeros(n,1);flag=1;% 消元过程for k=1:n-1for i=k+1:nif abs(A(k,k))>epsA(i,k+1:n+1)=A(i,k+1:n+1)-A(k,k+1:n+1)*A(i,k)/A(k,k);elseflag=0;returnendendend% 回代过程if abs(A(n,n))>epsx(n)=A(n,n+1)/A(n,n);elseflag=0;returnendfor i=n-1:-1:1x(i)=(A(i,n+1)-A(i,i+1:n)*x(i+1:n))/A(i,i);endreturnxA = 11 -3 -2 3-23 11 1 01 2 2 -1x = 0.21240.5492-1.15544、用Cholesky分解法解方程组3 2 3 x1 52 2 0 x2 33 0 12 x3 7解：.A=[3 2 3;2 2 0;3 0 12];b=[5 3 7];lambda=eig(A);if lambda>eps&isequal(A,A')[n,n]=size(A);R=chol(A);%解R'y=by(1)=b(1)/R(1,1);if n>1for i=2:ny(i)=(b(i)-R(1:i-1,i)'*y(1:i-1)')/R(i,i);endend%解Rx=yx(n)=y(n)/R(n,n);if n>1for i=n-1:-1:1x(i)=(y(i)-R(i,i+1:n)*x(i+1:n)')/R(i,i);endendx=x';elsex=[];disp('该方法只适用于对称正定的系数矩阵!');endR= 1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321y= 2.8868 -0.4082 0.5774x= 1.0000 0.5000 0.33335. 用列主元Doolittle分解法解方程组解：A=[3 4 5; -1 3 4; -2 3 -5;]; 3 4 5 X1 2 b=[2,-2 6]'; -1 3 4 X2 -2 [L,U,pv]=luex(A); -2 3 -5 X3 6y = L\b(pv);x = U\y结果如下：x = 11-114.已知，计算.解：A=[100 99;99 98];cond(A,inf)ans =3.9601e+04cond(A,2)ans =3.9206e+0427.编写LU分解法，改进平方根法，追赶法的Matlab程序，并进行相关数值试验。

第一章 绪论（12）1、设0>x ，x 的相对误差为δ，求x ln 的误差。

[解]设0*>x 为x 的近似值，则有相对误差为δε=)(*x r ，绝对误差为**)(x x δε=，从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x ， 相对误差为****ln ln )(ln )(ln x x x x rδεε==。

2、设x 的相对误差为2%，求n x 的相对误差。

[解]设*x 为x 的近似值，则有相对误差为%2)(*=x r ε，绝对误差为**%2)(x x =ε，从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε，相对误差为%2)()(ln )(ln ***n x x x nr==εε。

3、下列各数都是经过四舍五入得到的近似数，即误差不超过最后一位的半个单位，试指出它们是几位有效数字：1021.1*1=x ，031.0*2=x ，6.385*3=x ，430.56*4=x ，0.17*5⨯=x 。

[解]1021.1*1=x 有5位有效数字；0031.0*2=x 有2位有效数字；6.385*3=x 有4位有效数字；430.56*4=x 有5位有效数字；0.17*5⨯=x 有2位有效数字。

4、利用公式（3.3）求下列各近似值的误差限，其中*4*3*2*1,,,x x x x 均为第3题所给的数。

（1）*4*2*1x x x ++；[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε；（2）*3*2*1x x x ；[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε；（3）*4*2/x x 。

数值分析课后习题及答案第一章绪论（12）第二章插值法（40-42）2、当时，，求的二次插值多项式。

[解]。

3、给出的数值表用线性插值及二次插值计算的近似值。

X 0.4 0.5 0.6 0.7 0.8 -0.916291 -0.693147 -0.510826 -0.357765 -0.223144 [解]若取，，则，，则，从而。

若取，，，则，，，则，从而补充题：1、令，，写出的一次插值多项式，并估计插值余项。

[解]由，可知，，余项为，故。

2、设，试利用拉格朗日插值余项定理写出以为插值节点的三次插值多项式。

[解]由插值余项定理，有，从而。

5、给定数据表：，1 2 4 6 7 4 1 0 1 1 求4次牛顿插值多项式，并写出插值余项。

[解]一阶差商二阶差商三阶差商四阶差商 1 42 1 -34 0 6 17 1 0 由差商表可得4次牛顿插值多项式为：，插值余项为。

第三章函数逼近与计算（80-82）26、用最小二乘法求一个形如的经验公式，使它与下列数据相拟合，并求均方误差。

19 25 31 38 44 19.0 32.3 49.0 73.3 97.8[解]由。

又，，，故法方程为，解得。

均方误差为。

27、观测物体的直线运动，得出以下数据：时间t（秒）0 0.9 1.9 3.0 3.9 5.0 距离s（米）0 10 30 5080 110 [解]设直线运动为二次多项式，则由。

，。

又，，，故法方程为，解得。

故直线运动为。

补充题：1、现测得通过某电阻R的电流I及其两端的电压U如下表：I ……U ……试用最小二乘原理确定电阻R的大小。

[解]电流、电阻与电压之间满足如下关系：。

应用最小二乘原理，求R使得达到最小。

对求导得到：。

令，得到电阻R为。

2、对于某个长度测量了n次，得到n个近似值，通常取平均值作为所求长度，请说明理由。

[解]令，求x使得达到最小。

对求导得到：，令，得到，这说明取平均值在最小二乘意义下误差达到最小。