广东省广州市白云区汇侨中学九年级数学《弦切角定理》课件

初三数学弦切角及和圆有关的比例线段知识精讲一. 本周教学内容：弦切角及和圆有关的比例线段二. 重点、难点：1. 弦切角的概念：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

注意：弦切角必须具备三个条件：（1）顶点在圆上（切点），（2）一边和圆相切，（3）一边和圆相交（弦），三者缺一不可。

2. 弦切角定理：弦切角等于它所夹的弧对的圆周角。

3. 弦切角定理的推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等。

弦切角是和圆有关的角之一，其他几种有圆心角、圆周角、圆内接四边形的外角。

这四种角之间的关系及转换是与圆有关的论证及计算的基础。

4. 相交弦定理：圆内两条相交弦，被交点分成的两条线段长的积相等。

5. 相交弦定理的推论：如果弦与直径相交，那么弦的一半是它分直径所成的两条线段的比例中项。

6. 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

7. 切割线定理的推论（或称割线定理）：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

本节是本章中综合性最强的部分，是本章及初中平面几何中难点之一。

其中，相交弦定理、切割线定理及割线定理在证明等积式、比例式和线段长度的计算中起着极其重要的作用。

这三个定理实际是一个整体，可以看做相交弦交点从圆内移到圆外，由割线旋转到切线时的结果。

应用定理和推论解题时，要注意数形结合的思想、方程思想的运用。

由于定理和推论的结论都是两条线段乘积的形式，所以一元二次方程更显威力。

例1. 如图，经过⊙O求证：∠ATC＝∠证明一：∵TC为⊙∵∠TBC＝∠A＋∠∴∠TBC＝∠BTC即∠ATC＝∠TBC证明二：∵∠ETA又∵∠ATC＝180°－∠ETA ∠TBC＝180°－∠TBA104，==AB PABP6∴=OP OC CO =∴⨯=-∴=564549222，， CO CO >∴=07，答：⊙O 半径为7cmOD =24，进而求出例3. 如图，△ABC （1）求证：AE 2＝PE （2）若AE ＝4，PE （1）证明：∵PA ∵PF//AC ，∴∠C 又∠∠ AEP = ∴=∴AE DE PEBE， BD DC PF AC =，// ∴=BE AE∴=⋅AE PE DE 2（2）解：根据相交弦定理：AE ·BE ＝GE ·EF AE EF GE GE ==∴4=⋅∴=48822，，， PE PG PE GE =∴=-=-=5523，∴=+=+=PF PE EF 5813 ∵PA 是⊙O 的切线∴=⋅=⨯=PA PG PF 23133939＝15，sin C =35，求Rt △AD 、DB 的比值，又 解：连结OD 、DB∵CD 是⊙O 切线，∴OD ⊥CD 在中，Rt ODC C OD OC ∆sin ==35设，，则OD k OC k DC k ===354OD OB BC k k k AB k =∴=-==，，5326 ∠=∠∠=∠CDB A C C ， ∴∆∆CDB CAD ~∴===DB AD BC CD k k 2412AD DB AD =∴==151275，.∵AB 是⊙O 直径 ∴∠=︒ADB 90 ()∴=+=+=AB AD DB 222215751525. ∴=61525k ∴==BC k 2525注意：将Rt △ADB 中，DB 、AD 两边的比转化为切线、割线的比，（即）在这类图形中常用。

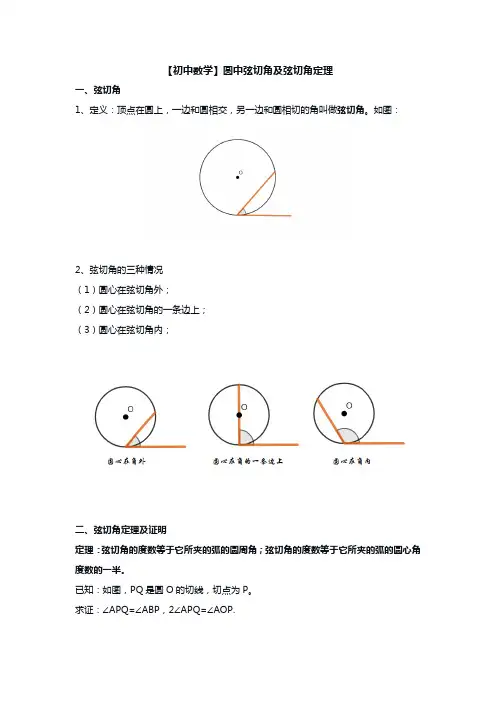
【初中数学】圆中弦切角及弦切角定理一、弦切角1、定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

如图：2、弦切角的三种情况（1）圆心在弦切角外；（2）圆心在弦切角的一条边上；（3）圆心在弦切角内；二、弦切角定理及证明定理：弦切角的度数等于它所夹的弧的圆周角；弦切角的度数等于它所夹的弧的圆心角度数的一半。

已知：如图，PQ是圆O的切线，切点为P。

求证：∠APQ=∠ABP，2∠APQ=∠AOP.（1）当圆心在弦切角外部时证明：连接OA，OP，在非弦切角所夹弧优弧PA上任取一点B，连接BP和BA。

∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠POA=180°∴2∠OPA+∠POA=180°∵ PO为圆的切线，OP为半径∴ ∠OPA+∠APQ=90°∴ ∠OPA=90°-∠APQ∴ 2（90°-∠APQ）+∠POA=180°∴∠POA=2∠APQ∵ ∠POA=2∠ABP（同弧所对的圆心角是圆周角的2倍）∴ ∠APQ=∠ABP（2）当圆心在弦切角的一边上时证明：在非弦切角所夹弧AP上任取一点B，连接AB、PB ∵ AP为直径∴ ∠ABP=90°∵ PQ为圆的切线，OP为半径∴ ∠APQ=90°∴∠APQ=∠ABP∴2∠APQ=∠AOP（同弧所对的圆心角是圆周角的2倍）. （3）当圆心在弦切角的内部时证明：连接OA，OP，在非弦切角所夹弧劣弧PA上任取一点B，连接BP和BA。

∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠1=180°∴2∠OPA+∠1=180°∵ PO为圆的切线，OP为半径∴ ∠OPA=∠APQ-90°∴ 2（∠APQ-90°）+∠1=180°∴ ∠1+2∠APQ=360°∵ ∠1+∠2=360°∴∠2=2∠APQ∴ ∠POA=2∠APQ（这里的∠POA是大于180°的角，是优弧AP所对的圆心角）∵ ∠POA=2∠ABP（同弧所对的圆心角是圆周角的2倍）∴ ∠APQ=∠ABP三、例题例1、已知：如图，直线BC切⊙O于B点，AB=AC，AD=BD，求∠A．解：由弦切角定理可得，∠DBC=∠A∵ AD=BD∴ ∠A=∠ABD∵ AB=AC∴ ∠ABC=∠ACB=2∠A∵ ∠A+∠ABC+∠ACB=180°∴5∠A=180°∴ ∠A=36°例2、已知：如图，直线DC与⊙O相切于点C，AB为⊙O直径，AD⊥DC于D，∠DAC=28°，求∠CAB的值。