二次函数的应用(第三课时)

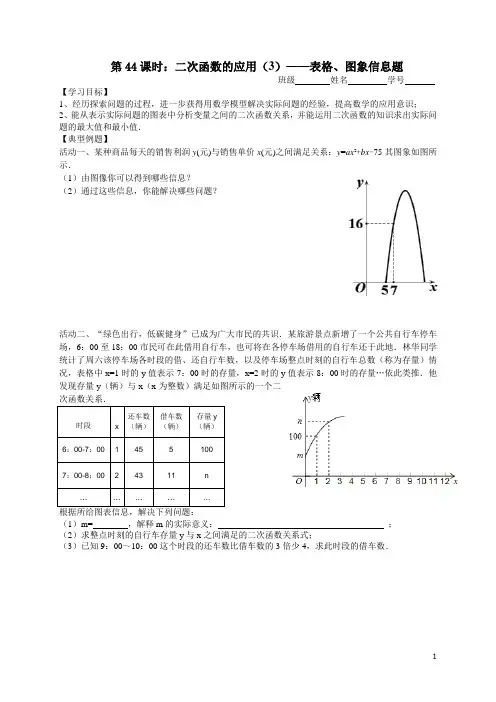
第44课时：二次函数的应用（3）——表格、图象信息题班级姓名学号【学习目标】1、经历探索问题的过程，进一步获得用数学模型解决实际问题的经验，提高数学的应用意识；2、能从表示实际问题的图表中分析变量之间的二次函数关系，并能运用二次函数的知识求出实际问题的最大值和最小值．【典型例题】活动一、某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系：y=ax²+bx-75其图象如图所示．（1）由图像你可以得到哪些信息？（2）通过这些信息，你能解决哪些问题？活动二、“绿色出行，低碳健身”已成为广大市民的共识．某旅游景点新增了一个公共自行车停车场，6：00至18：00市民可在此借用自行车，也可将在各停车场借用的自行车还于此地．林华同学统计了周六该停车场各时段的借、还自行车数，以及停车场整点时刻的自行车总数（称为存量）情况，表格中x=1时的y值表示7：00时的存量，x=2时的y值表示8：00时的存量…依此类推．他发现存量y（辆）与x（x为整数）满足如图所示的一个二次函数关系．时段x 还车数（辆）借车数（辆）存量y（辆）6：00-7：00 1 45 5 1007：00-8：00 2 43 11 n……………根据所给图表信息，解决下列问题：（1）m=，解释m的实际意义：；（2）求整点时刻的自行车存量y与x之间满足的二次函数关系式；（3）已知9：00～10：00这个时段的还车数比借车数的3倍少4，求此时段的借车数．活动三、某水果店新进一种水果，进价为20元/盒，为了摸清行情，决定试营销10天，商家通过这10天的市场调查发现：①销售价y（元/盒）与销售天数x（天）满足以下关系：天数1≤x≤56≤x≤10销售价格y2421x30②每天的销售量p（盒数）与销售天数x关系如图所示．（1）试求每天的销售量p（盒数）与销售天数x之间函数关系式；（2）设水果店的销售利润为s（元），求销售利润s（元）与销售天数x（天）之间的函数关系式，并求出试营销期间一天的最大利润．。

卖花进行中漫画释义满分晋级3函数13级 二次函数的基本解析式与图象变换函数14级 二次函数 实际应用 函数15级 二次函数 图象综合应用暑期班 第二讲暑期班 第三讲秋季班第三讲二次函数实际应用中考内容中考要求A B C二次函数了解二次函数的意义；会用描点法画出二次函数的图象能通过分析实际问题的情境确定二次函数的解析式；能从图象上认识二次函数的性质；会根据二次函数的解析式求其图象与坐标轴的交点坐标，会确定图象的顶点、开口方向和对称轴；会利用二次函数的图象求一元二次方程的近似解能用二次函数解决简单的实际问题；能解决二次函数与其他知识综合的有关问题二次函数在北京中考中属于必考考点，并且都以压轴题形式出现，是中考的难点，也是同学们失分最高的一部分。

这部分内容要求学生们⑴能用数形结合、归纳等数学思想，根据二次函数的表达式确定二次函数的开口方向、对称轴和顶点坐标；⑵综合运用方程、几何、函数等知识解决实际问题。

年份2010年2011年2012年题号24 7，8，23 8，23分值8分11分11分考点确定抛物线的解析式，二次函数与等腰直角三角形综合抛物线顶点坐标；函数图象；二次函数和一次函数解析式（函数图象与坐标轴交点、函数图象交点坐标），二次函数与一元二次方程（判别式、求根）函数图象；二次函数的对称性；二次函数和一次函数解析式（函数图象与坐标轴交点、函数图象交点坐标）；二次函数图象平移，利用函数图象求取值范围中考考点分析中考内容与要求知识互联网实际应用问题主要考查涨降价、面积等问题，讲解时要明确等量关系．【例1】 如图，线段AB 的长为2，C 为AB 上一个动点，分别以AC 、BC 为斜边在AB 的同侧作两个等腰直角三角形△ACD 和△BCE ，则求DE 长的最小值．（2012扬州）EDB C A EDBC A【解析】 如图，连接DE ．设x AC =则x BC -=2，∵△ACD 和△BCE 分别是等腰直角三角形，∴∠DCA ＝45°，∠ECB ＝45°，DC ＝x 22，CE ＝()x -222， ∴∠DCE ＝90°， 故()()1122221212222222+-=+-=-+=+=x x x x x CE DC DE ， 当1=x 时，2DE 取得最小值，DE 也取得最小值，最小值为1． 故答案为：1．夯实基础模块一 实际应用问题知识导航【例2】 某商品的进价为每件50元，售价为每件60元，每个月可卖出200件。

1.利用函数图象判断下列方程有没有解，有几个解.若有解，求出它的解（精确到0.1）.(1)01212=+-x x . (2)0132=+-x x .【答案】(1)作出函数1212+-=x x y 的图像（图略），可知方程01212=+-x x 没有解. (2)作出函数132+-=x x y 的图像（图略），可知方程0132=+-x x 有两个解.可得两解为..,.624021≈≈x x2.用两种不同的图解法求方程0522=--x x 的解（精确到0.1）.【答案】解法一：作出函数522--=x x y 的图象观察图象（如下图），与曾轴交点的横坐标可得方程的解为..,.434121≈-≈x x解法二：分别作出函数2x y =与52+=x y 的图象（如下图），观察函数图象交点的横坐标，可得方程的解为..,.434121≈-≈x x3.某拱形门建筑的形状是抛物线援若取拱形门地面上两点的连线为x 轴，它可以近似地用函数194979722+--=)(x y 表示（单位：m ）援问：拱形门底部大约有多宽？有多高？ 【答案】令0=y ，则0194979722=+--)(x ，解得.,194021==x x ∴拱形门大约194m 宽，194m 高.4.某农场拟建两间矩形种牛饲养室，饲养室的一面靠现有墙（墙长＞50m ），中间用一道墙隔开（如图）.已知计划中的建筑材料可建围墙的总长为50m ，设两间饲养室合计长x （m ），总占地面积为y （m 2）.(1)求赠关于曾的函数表达式和自变量的取值范围.(2)画出函数的图象.(3)利用图象判断：若要使两间饲养室占地总面积达到200m 2，则各道墙的长度为多少？占地总面积有可能达到210m 2吗？【答案】(1),x x y 350312+-=其中.500<<x (2)图略.(3)当200=y 时，可得20=x 或.30=x∴各道墙的长度分别为20m,10m 或30m ，320m 时,y 有最大值2103625<， ∴占地总面积不可能达到210m 2.5.已知一个二次函数的图象与曾轴的交点为（－2，0），（4 ，0 ），且顶点在函数y ＝2x 的图象上.求这个二次函数的表达式.【答案】设所求函数表达式为).)((42-+=x x a y 顶点的横坐标为x =1，则顶点的纵坐标为y=2.把顶点坐标（1，2）代入上述表达式，得2=-9a ，∴92-=a .所以所求函数表达式为))((4292-+-=x x y .。

B A O二次函数应用导学案一、情景创设例 1 如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O 恰在水面中心,OA=1.25m.由柱子顶端A 处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA 距离为1m 处达到距水面最大高度2.25m.(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外？(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)？例 2 一场篮球赛中，球员甲跳起投篮如图所示，已知球出手时离地面920m ，与篮筐中心的水平距离是7m,当球运行的水平距离是4m 时，达到最大高度4m 。

设篮球运行的路线为抛物线，篮筐距地面3m 。

⑴问此球能否投中？⑵此时对方球员乙前来盖帽，已知乙跳起后摸到的最大高度为3.19m ，他如何做才能盖帽成功？巩固练习1、如图是某公园一圆形喷水池，水流在各方向沿形状相同的抛物线落下。

建立如图所示的坐标系，如果喷头所在处A （0，1.25），水流路线最高处B （1，2.25），则该抛物线的表达式为 。

如果不考虑其他因素，那么水池的半径至少要____米，才能使喷出的水流不致落到池外。

2、小明是学校田径队的运动员，根据测试资料分析，他掷铅球的出手高度（铅球脱手时离地面的高度）为2m 。

如果出手后铅球在空中飞行的水平距离x(m)与高度y （m ）之间的关系为二次函数y=a(x －4)2+3，那么小明掷铅球的出手点与铅球落地点之间的水平距离是多少（精确到0.1m ）？六、课堂作业1、在距离地面2m 高的某处把一物体以初速度v 0(m/s)竖直向上抛出，在不计空阻力的情况下，其上升高度s(m)与抛出时间t(s)满足s= v 0t －21gt 2（其中g 是常数，通常取10m/s 2），若v 0=10m/s ，则该物体在运动至最高点时距离地面 m.2、如图所示，小明在今年的校运动会跳远比赛中跳出院满意的成绩，函数h=3.51－4.9t 2+0.5(t 的单位：s ，h 的单位：m)可以描述他跳远时重心高度的变化，则他起跳后到重心最高所用的时间大约是A ．0.71sB ．0.70sC ．0.63sD ．0.6s3、某地要建造一个圆形喷水池，在水池中央垂直于水面安装一个装饰柱OA ，O恰在水面中心，柱子顶端A 处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，形状如图①。