高中数学知识网络图

高一数学必修1知识网络集合函数 附：一、函数的定义域的常用求法：1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函x 中x k π≠11法1123则y 45六、函数奇偶性的常用结论：1、如果一个奇函数在0x =处有定义，则(0)0f =，如果一个函数()y f x =既是奇函数又是偶函数，则()0f x =（反之不成立）2、两个奇（偶）函数之和（差）为奇（偶）函数；之积（商）为偶函数。

3、一个奇函数与一个偶函数的积（商）为奇函数。

4、两个函数()y f u =和()u g x =复合而成的函数，只要其中有一个是偶函数，那么该复合函数就是偶函数；当两个函数都是奇函数时，该复合函数是奇函数。

5、若函数()f x 的定义域关于原点对称，则()f x 可以表示为11()[()()][()()]22f x f x f x f x f x =+-+--，该式的特点是：右端为一个奇函数和一个偶函数高中数学必修2知识点一、直线与方程（1）直线的倾斜角定义：x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。

特别地，当直线与x 轴平行或重合时,我们规定它的倾斜角为0度。

因此，倾斜角的取值范围是0°≤α＜180°（2）直线的斜率①定义：倾斜角不是90°的直线，它的倾斜角的正切叫做这条直线的斜率。

直线的斜率常用k 表示。

即tan k α=。

斜率反映直线与轴的倾斜程度。

当[) 90,0∈α时，0≥k ；当() 180,90∈α时，0<k ；当 90=α时，k 不存在。

②过两点的直线的斜率公式：)(211212x x x x y y k ≠--=(2)k 与(4)（3注意：上每一注意：平行于（50=（C （ⅰ（ⅱ()()0222111=+++++C y B x A C y B x A λ（λ为参数），其中直线2l 不在直线系中。

（6）两直线平行与垂直当111:b x k y l +=，222:b x k y l +=时，212121,//b b k k l l ≠=⇔；12121-=⇔⊥k k l l注意：利用斜率判断直线的平行与垂直时，要注意斜率的存在与否。

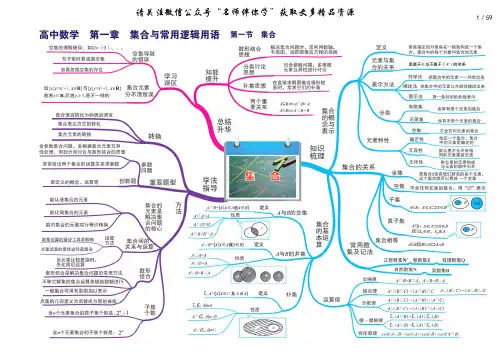
;;=⇔⊆=⇔⊆=⇔⊆A B B A B A B A A B A B I A Bn-个A中元素有n个，则A的子集共有2n个，真子集有21集合间的运算2n R a +∈则2n n a n a ++≥平均值不等式2nnn a a n++≥当且仅当2,,)n 时取等号1111221n j n j n n n a b a b a b a b a b a b ++≤++≤+++,n Z 是∀,,nx 是区间1122)()()()n n n n q x q f x q f x q f x ++≤+++,,,1n i q R q +∈=∑）。

上凸函数不等号转向.1}n ma+仍是等比数列，其公比为)lim n n a ++=sin sin αtan tan 1tan tan α±2(AB x =，则a ⊥b2PP 所成比112222221cos ||||a b a b a ba b a b a ++⋅⋅==⋅+212()(x x y y =-+-空间向量的直角坐标运算律若123(,,a a a a =，12(,,b b b b =则①113(a b a b +=+，11(a b a b -=-123(,)()a a a R λλλλλ=∈，11a b a b ⋅=+②13//a ba b λλ⇔=，110a b a b ⊥⇔+若111(,,)A x y z 则2(AB x =-模长公式若12(,,a a a a =21||a a a a a =⋅=+空间向量的运算,,(OB OA AB a b BA OA OB a b OP a λλ=+=+=-=-=空间向量的加减与数乘OB OA AB =+=a +b ，AB OB OA =-，,(OP λ=a a b + c ⑶数乘分配律：λ(a + ) =λa +λb ．平行六面体向量的数乘积||||cos ,a b a b a b ⋅=⋅⋅<>空间向量数乘积的性质①||cos ,a e a a e ⋅=<>．②0a b a b ⊥⇔⋅=．③2||a a a =⋅．空间向量数量积运算律①()()()a b a b a b λλλ⋅=⋅=⋅②a b b a ⋅=⋅（交换律） ③()a b c a b a c ⋅+=⋅+⋅（分配律）④e a = a e =|a |cos ,a e⑤ab a b = 0⑥当a 与b 同向时，a b = |a ||b |；当a 与b 反向时，a b = |a ||b |.特别的a a = |a |2或||a a a =⋅⑦cos ,||||a ba b a b ⋅=Bα∈，则l αβ=且l，则A、B、C 。

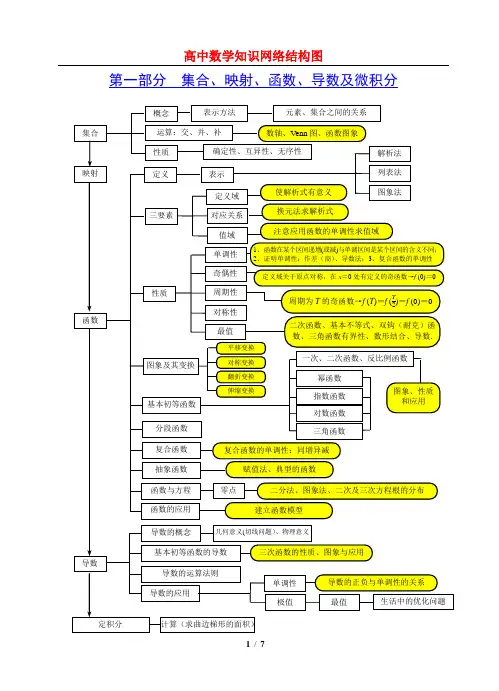
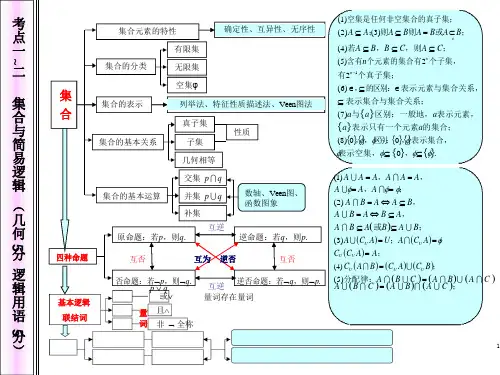
集合元素的特性确定性、互异性、无序性有限集集合的分类无限集空集φ集合的表示列举法、特征性质描述法、Veen 图法集合的基本关系真子集性质子集几何相等 集合的基本运算交集 p q并集 p q 补集互逆数轴、Veen 图、函数图象(1) A A = A ，A A = A ， A φ= A ，A φ= φ； (2) A B = A ⇔ A ⊆ B ， A B = A ⇔ B ⊆ A ，A B ⊆ A (或B )⊆ A B ；四种命题原命题：若p ，则q .互否否命题：若⌝p ，则⌝q .p ∨ q 互为 逆否互逆逆命题：若q ，则p .互否逆否命题：若⌝q ，则⌝p .(3) A (C U A ) = U ；A (C U A ) = φ； C U (C U A ) = A ；(4) C U (A B ) = (C U A ) (C U B )；(5)分配律：A (B C ) = (A B ) (A C ) A (B C ) = (A B ) (A C )；基本逻辑联结词量词 或∨且∧非 ⌝ 全称量词存在量词(1)空集是任何非空集合的真子集；(2) A ⊆ A ；(3)则A ⊆ B 则A = B 或A ⊂ B ；≠(4)若A ⊆ B ，B ⊆ C ，则A ⊆ C ； (5)含有n 个元素的集合有2n 个子集， 有2n -1个真子集；(6) ∈，⊆ 的区别：∈ 表示元素与集合关系， ⊆ 表示集合与集合关系；(7)a 与{a }区别：一般地，a 表示元素，{a }表示只有一个元素a 的集合； (8){0}，{φ}，φ区别：{0}，{φ}表示集合， φ表示空集，φ⊆ {0}，φ⊆ {φ}.集合考点一 二集合与简易逻辑（几何 分 逻辑用语 分~ 5 5p ∧q⌝p(或⌝q)全称命题存在命题(6)结合律：A(BC)=(AB)C；A(BC)=(AB)C；否若p:∀x∈M，p(x)；则⌝p:∃x∈M，⌝p(x0)定若p:∃x∈M，p(x0)；则⌝p:∀x∈M，⌝p(x)考点三函数概念与基本初等函数（奇偶性 分 ）5A 中元素在B 中都有唯一的象；可一对一 （一一映射），也可多对一，但不可一对多列表法定义函数的概念表示定义域 解析法图象法使解析式有意义及实际意义三要素 区间对应关系值域常用换元法求解析式观察法、判别式法、分离常数法、单调性法、最值法、重要不等式、三角法、图象法、线性规划等函数的基本性质单调性奇偶性周期性对称性最值1.求单调区间：定义法、导数法、用已知函数的单调性。