18.微专题:圆中的几何变换、动点问题【河北热点】
- 格式:ppt
- 大小:1.90 MB
- 文档页数:12

圆的动点专题讲解一、教材分析动点问题在初中数学中虽然没有编入课本,但却是习题中的常见形式。
也是初中学生学习数学中的一大难点。
涉及到的题目类型也很多,而与圆有关的动点问题是仅次于二次函数动点问题的一部分,因此,解决这类动点问题,找出合理的方法和规律,就显得特别重要了。
二教学目标知识与技能:1、掌握解动点问题的方法2、熟练运用线圆相切、圆圆相切的判定条件来判断它们的位置关系。
过程与方法:1、利用运动的特征帮助探索圆的移动距离2、数形结合、方程思想的运用情感态度价值观:通过动手操作、合作交流,探索证明等活动,培养学生的团队合作精神,激发学生学习数学的兴趣。
三、教学重难点:教学重点:根据动点中的移动距离,找出等量列方程。
教学难点:1、两物同时运动时的距离变化2、移动题型中的分类讨论四、说教学方法:为了让学生能够更加直观形象的理解动点问题,本课准备采取动手操作加学生讨论交流的方法进行,并辅助以多媒体课件教学,准备教具如下:1 如图,点A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长的速度运动,运动时间为t秒.(1)求点C的坐标;(2)当∠BCP=15°,求t的值;(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD 的边(或边所在的直线)相切时,求t的值.【分析】(1)因为∠CBO=45,B(-3,0)∴△BOC是等腰直角三角形,∴OC=OB,∴C(0,3)(2)当∠BCP=15°时,有2种情况,点P在点B的左侧和右侧,在左侧时,∠PCO=30°,右侧时,∠PCO=60°,根据OC=3可以求出OP的长度,则PQ=OQ+OP 可以求出t值(3)若⊙P与四边形的边或所在直线相切,则可知⊙P与AB边不可能相切,只有3种情况⊙P与BC边相切时,切点为C,即PC⊥BC,根据等腰直角三角形可以求出OP的长度及PQ长⊙P与DC相切时,切点是C,PC⊥DC,∵OC⊥DC,∴点P与点O重合⊙与AD相切时,切点为A,及PA=PC,设OP=m,则AP=PC=5-M 根据直角三角形POC列方程可解出m的值,即可知道PQ的长度2如图1,在矩形ABCD中,AB=20 cm,BC=4 cm,点P从A开始沿折线A—B—C—D以4 cm / s的速度移动,点Q从C开始沿CD边以1 cm / s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动.设运动时间为t(s).(1) t为何值时,四边形APQD为矩形?(2) 如图2,如果⊙P和⊙Q的半径都是2 cm,那么t为何值时,⊙P和⊙Q外切?分析:1)四边形APQD为矩形,必须为平行四边形,只需要AP=DQ即可2)Q点始终位于边CD上,但是P点分别位于边AB, 边BC,边CD上,特别是P 点在边CD上有两种情形,所以一共有4种情形,答案不一定有4个,必须根据题目的条件求解。

专题六圆的有关动点综合问题【类型综述】综合题是指学生在不同的学习阶段所学的知识,不同章节所学的知识,特别是代数、几何不同学科中所学的知识,综合运用进行解题的数学题目,它既能考察同学们对数学基础知识基本方法掌握的熟练程度,又能考察综合运用数学知识分析问题、解决问题的能力。
几何中关于圆的综合题大致可分为:(1)以几何知识为主体的综合题;(2)代数、几何知识相结合的综合题;(3)圆中的探索型问题;【方法揭秘】直线与圆的位置关系问题,一般也无法先画出比较准确的图形.解这类问题,一般也分三步走,第一步先罗列两要素:R和d,第二步列方程,第三步解方程并验根.第一步在罗列两要素R和d的过程中,确定的要素罗列出来以后,不确定的要素要用含有x的式子表示.第二步列方程,就是根据直线与圆相切时d=R列方程.如图1,直线443y x=+与x轴、y轴分别交于A、B两点,圆O的半径为1,点C在y轴的正半轴上,如果圆C既与直线AB相切,又与圆O相切,求点C的坐标.“既……,又……”的双重条件问题,一般先确定一个,再计算另一个.假设圆C与直线AB相切于点D,设CD=3m,BD=4m,BC=5m,那么点C的坐标为(0,4-5m).罗列三要素:对于圆O,r=1;对于圆C,R=3m;圆心距OC=4-5m.分类列方程:两圆外切时,4-5m=3m+1;两圆内切时,4-5m=3m-1.把这个问题再拓展一下,如果点C在y轴上,那么还要考虑点C在y轴负半轴.相同的是,对于圆O,r=1;对于圆C,R=3m;不同的是,圆心距OC=5m-4.图1【典例分析】例1 如图1,直线AB与x轴交于点A(-4, 0),与y轴交于点B(0, 3).点P从点A出发,以每秒1个单位长度的速度沿直线AB向点B移动.同时将直线34y x=以每秒0.6个单位长度的速度向上平移,交OA于点C,交OB于点D,设运动时间为t(0<t<5)秒.(1)证明:在运动过程中,四边形ACDP总是平行四边形;(2)当t取何值时,四边形ACDP为菱形?请指出此时以点D为圆心、OD长为半径的圆与直线AB 的位置关系并说明理由.图1例2如图1,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆上运动(包含P、Q两点),以线段AB为边向上作等边三角形ABC.(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(如图1);(2)设∠AOB=α,当线段AB与圆O只有一个公共点(即A点)时,求α的范围(如图2,直接写出答案);(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长(如图3).图1 图2 图3例3在Rt △ABC 中,∠C =90°,AC =6,53sin B ,⊙B 的半径长为1,⊙B 交边CB 于点P ,点O 是边AB 上的动点.(1)如图1,将⊙B 绕点P 旋转180°得到⊙M ,请判断⊙M 与直线AB 的位置关系; (2)如图2,在(1)的条件下,当△OMP 是等腰三角形时,求OA 的长;(3)如图3,点N 是边BC 上的动点,如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切,设NB =y ,OA =x ,求y 关于x 的函数关系式及定义域.图1 图2 图3例4如图1,在Rt △ABC 中,∠ACB =90°,AC =4,cos A =14,点P 是边AB 上的动点,以P A 为半径作⊙P .(1)若⊙P 与AC 边的另一个交点为D ,设AP =x ,△PCD 的面积为y ,求y 关于x 的函数解析式,并直接写出函数的定义域;(2)若⊙P 被直线BC 和直线AC 截得的弦长相等,求AP 的长;(3)若⊙C 的半径等于1,且⊙P 与⊙C ,求AP 的长.图1 备用图例5如图1,抛物线y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和1)16两点,点P 在该抛物线上运动,以点P 为圆心的⊙P 总经过定点A (0, 2).(1)求a 、b 、c 的值;(2)求证:在点P 运动的过程中,⊙P 始终与x 轴相交;(3)设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标.图1【变式训练】1.(2017北京第29题)在平面直角坐标系xOy 中的点P 和图形M ,给出如下的定义:若在图形M 上存在一点Q ,使得P Q 、两点间的距离小于或等于1,则称P 为图形M 的关联点. (1)当O 的半径为2时,①在点123115,0,,,,02222P P P ⎛⎛⎫⎛⎫ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭中,O 的关联点是_______________. ②点P 在直线y x =-上,若P 为O 的关联点,求点P 的横坐标的取值范围.(2)C 的圆心在x 轴上,半径为2,直线1y x =-+与x 轴、y 轴交于点A B 、.若线段AB 上的所有点都是C 的关联点,直接写出圆心C 的横坐标的取值范围.2. (2017广东广州第25题)如图14,AB 是O 的直径,,2AC BC AB ==,连接AC .(1)求证:045CAB ∠=; (2)若直线l 为O 的切线,C 是切点,在直线l 上取一点D ,使,BD AB BD =所在的直线与AC 所在的直线相交于点E ,连接AD .①试探究AE 与AD 之间的数量关系,并证明你的结论; ②EBCD是否为定值?若是,请求出这个定值;若不是,请说明理由.3. (2017湖南湘潭第26题)如图,动点M 在以O 为圆心,AB 为直径的半圆弧上运动(点M 不与点A B 、及AB 的中点F 重合),连接OM .过点M 作ME AB ⊥于点E ,以BE 为边在半圆同侧作正方形BCDE ,过M 点作O 的切线交射线DC 于点N ,连接BM 、BN .(1)探究:如左图,当M 动点在AF 上运动时; ①判断OEM MDN ∆∆是否成立?请说明理由;②设ME NCk MN+=,k 是否为定值?若是,求出该定值,若不是,请说明理由;③设MBN α∠=,α是否为定值?若是,求出该定值,若不是,请说明理由; (2)拓展:如右图,当动点M 在FB 上运动时;分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)4. (2017湖南株洲第26题)已知二次函数y=﹣x2+bx+c+1,①当b=1时,求这个二次函数的对称轴的方程;②若c=14b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?③若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足13DEEF,求二次函数的表达式.5. (2017哈尔滨第26题)已知:AB 是O ⊙的弦,点C 是AB 的中点,连接OB 、OC ,OC 交AB 于点D . (1)如图1,求证:AD BD =;(2)如图2,过点B 作O ⊙的切线交OC 的延长线于点M ,点P 是AC 上一点,连接AP 、BP ,求证:90APB OMB -=∠∠°.(3)如图3,在(2)的条件下,连接DP 、MP ,延长MP 交O ⊙于点Q ,若6MQ DP =,3sin 5ABO =∠,求MP MQ 的值.6. (2017年贵州省黔东南州第24题)如图,⊙M 的圆心M (﹣1,2),⊙M 经过坐标原点O ,与y 轴交于点A ,经过点A 的一条直线l 解析式为:y=﹣x+4与x 轴交于点B ,以M 为顶点的抛物线经过x 轴上点D (2,0)和点C (﹣4,0). (1)求抛物线的解析式; (2)求证:直线l 是⊙M 的切线;(3)点P 为抛物线上一动点,且PE 与直线l 垂直,垂足为E ,PF ∥y 轴,交直线l 于点F ,是否存在这样的点P ,使△PEF 的面积最小?若存在,请求出此时点P 的坐标及△PEF 面积的最小值;若不存在,请说明理由.7.(2017年四川省内江市第27题)如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE.(1)求证:AC2=AE•AB;(2)过点B作⊙O的切线交EC的延长线于点P,试判断PB与PE是否相等,并说明理由;(3)设⊙O半径为4,点N为OC中点,点Q在⊙O上,求线段PQ的最小值.8. (2017年浙江省杭州市第23题)如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,(1)点点同学通过画图和测量得到以下近似数据:猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.9.(2017浙江温州第24题)(本题14分)如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD 上),连结AC,DE.(1)当∠APB=28°时,求∠B和CM的度数;(2)求证:AC=AB。

初一几何动点问题的解题技巧解决初一几何动点问题的关键在于理解动点的概念并熟练运用相关的几何性质和解题技巧。
以下是几个常用的解题技巧:1. 确定动点的位置:首先,要明确问题中动点的位置信息。
通过观察题目中的几何图形,确定动点所在的线段、圆弧或多边形等位置。
2. 使用变量表示:用变量来表示动点的坐标或长度。
常见的表示方式可以使用字母如"A"、"B"等来表示动点,使用"x"、"y"等来表示坐标。
3. 利用几何性质:根据几何图形的性质,运用传统的几何知识来推导和解决问题。
例如,利用直角三角形的性质、相似三角形的性质、平行线的性质等。
4. 延长线和引出辅助线:有时候,延长线或引出辅助线可以帮助我们更好地理解问题和得出结论。
通过引出合适的辅助线,可以简化或改变问题的形式,使得解题更容易。
5. 利用相关定理和公式:了解和掌握基本的几何定理和公式,如勾股定理、正弦定理、余弦定理等。
在解决动点问题时,这些定理和公式常常可以提供有用的信息和关键的方程式。
6. 理清逻辑关系和方向:动点问题往往涉及到几何图形之间的相对方向和关系,如垂直、平行、相交等。
在解题过程中,要仔细分析这些关系,并据此推导出正确的结论。
7. 尝试特殊情况:有时候,特殊情况下的解法能够启发我们找到普遍情况下的解法。
可以尝试选择特殊的数值或角度,验证一些猜想,从而推导出一般情况的结论。
8. 画图辅助解题:通过绘制几何图形,可以更直观地理解问题,并更好地分析和推导解题过程。
要善于利用图形和图形性质来辅助解题。
以上是一些初一几何动点问题的解题技巧,希望能对您有所帮助。
请记住,多多练习和思考,通过实践来提高解题能力。


2014年中考数学专题复习:与圆有关的动点问题1、如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线DC,P点为优弧CBA上一动点(不与A.C重合).(1)求∠APC与∠ACD的度数;(2)当点P移动到CB弧的中点时,求证:四边形OBPC是菱形.(3)P点移动到什么位置时,△APC与△ABC全等,请说明理由.2、如图,在⊙O上位于直径AB的异侧有定点C和动点P,AC=12AB,点P在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD交PB于D点.(1)如图1,求证:△PCD∽△ABC;(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.3、如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.(1)当BC=1时,求线段OD的长;(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.4、如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.(1)当P异于A.C时,请说明PQ∥BC;(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?5、如图,在菱形ABCD中,AB=23,∠A=60º,以点D为圆心的⊙D与边AB相切于点E.(1)求证:⊙D与边BC也相切;(2)设⊙D与BD相交于点H,与边CD相交于点F,连接HF,求图中阴影部分的面积(结果保留π);(3)⊙D上一动点M从点F出发,按逆时针方向运动半周,当S△HDF=3S△MDF时,求动点M经过的弧长(结果保留π).6、半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,⊙O与l相切于点F,DC在l上.(1)过点B作的一条切线BE,E为切点.①填空:如图1,当点A在⊙O上时,∠EBA的度数是;②如图2,当E,A,D三点在同一直线上时,求线段OA的长;(2)以正方形ABCD的边AD与OF重合的位置为初始位置,向左移动正方形(图3),至边BC与OF重合时结束移动,M,N分别是边BC,AD与⊙O的公共点,求扇形MON的面积的范围.7、如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.(1)直接写出线段AC、AD及⊙O半径的长;(2)设PH=x,PC=y,求y关于x的函数关系式;(3)当PH与⊙O相切时,求相应的y值.8、如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.(1)求证:OF∥BE;(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.9、如图,⊙O 的半径为1,直线CD 经过圆心O ,交⊙O 于C 、D 两点,直径AB ⊥CD ,点M 是直线CD 上异于点C 、O 、D 的一个动点,AM 所在的直线交于⊙O 于点N ,点P 是直线CD 上另一点,且PM=PN .(1)当点M 在⊙O 内部,如图一,试判断PN 与⊙O 的关系,并写出证明过程; (2)当点M 在⊙O 外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由; (3)当点M 在⊙O 外部,如图三,∠AMO=15°,求图中阴影部分的面积.10、如图,在⊙O 中,直径AB ⊥CD ,垂足为E ,点M 为OC 上动点,AM 的延长线交⊙O 于点G ,交过C 的直线于F ,∠1=∠2,连结CB 与DG 交于点N . (1)求证:CF 是⊙O 的切线;(2)点M 在OC 上移动时(点M 不与O 、C 点重合),探究△ACM 与△DCN 之间关系,并证明 (3)若点M 移动到CO 的中点时,⊙O 的半径为4,cos ∠BOC=41,求BN 的长.11、如图,已知AB 是圆O 的直径,BC 是圆O 的弦,弦ED ⊥AB 于点F,交BC于点G,过点C作圆O的切线与ED的延长线交于点P.(1)求证:PC=PG;(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;(3)在满足(2)的条件下,已知圆为O的半径为5,若点O到BC时,求弦ED的长.12、如图1,已知⊙O的半径长为3,点A是⊙O上一定点,点P为⊙O上不同于点A的动点.(1)当1A=时,求AP的长;tan2(2)如果⊙Q过点P、O,且点Q在直线AP上(如图2),设AP=x,QP=y,求y关于x的函数关系式,并写出函数的定义域;(3)在(2)的条件下,当4A=时(如图3),存在⊙M与⊙O相内切,同时与⊙Qtan3相外切,且OM⊥OQ,试求⊙M的半径的长.图1 图2 图3答案:1、解:(1)连接AC ,如图所示:∵AB=4,∴OA=OB=OC=12AB=2。
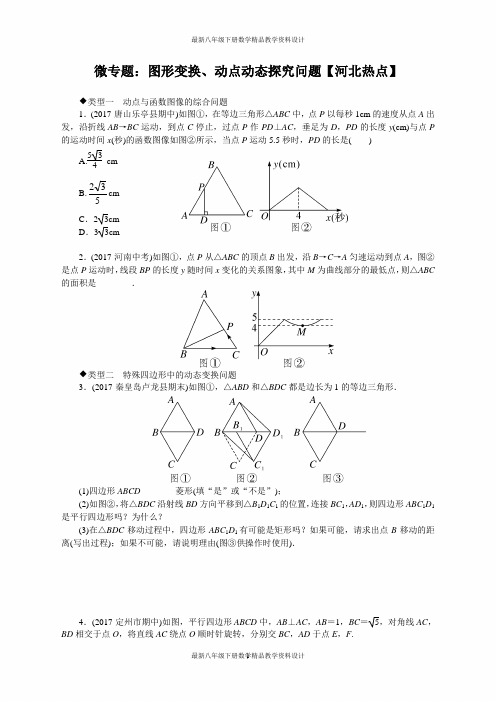
微专题:图形变换、动点动态探究问题【河北热点】◆类型一 动点与函数图像的综合问题1.(2017·唐山乐亭县期中)如图①,在等边三角形△ABC 中,点P 以每秒1cm 的速度从点A 出发,沿折线AB →BC 运动,到点C 停止,过点P 作PD ⊥AC ,垂足为D ,PD 的长度y (cm)与点P 的运动时间x (秒)的函数图像如图②所示,当点P 运动5.5秒时,PD 的长是( ) A.534cm B.532cm C .23cmD .33cm2.(2017·河南中考)如图①,点P 从△ABC 的顶点B 出发,沿B →C →A 匀速运动到点A ,图②是点P 运动时,线段BP 的长度y 随时间x 变化的关系图象,其中M 为曲线部分的最低点,则△ABC 的面积是________.◆类型二 特殊四边形中的动态变换问题3.(2017·秦皇岛卢龙县期末)如图①,△ABD 和△BDC 都是边长为1的等边三角形.(1)四边形ABCD ________菱形(填“是”或“不是”);(2)如图②,将△BDC 沿射线BD 方向平移到△B 1D 1C 1的位置,连接BC 1,AD 1,则四边形ABC 1D 1是平行四边形吗?为什么?(3)在△BDC 移动过程中,四边形ABC 1D 1有可能是矩形吗?如果可能,请求出点B 移动的距离(写出过程);如果不可能,请说明理由(图③供操作时使用).4.(2017·定州市期中)如图,平行四边形ABCD 中,AB ⊥AC ,AB =1,BC =5,对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交BC ,AD 于点E ,F .(1)当∠AOF=90°时,求证:四边形ABEF是平行四边形;(2)试说明在旋转过程中,AF与CE总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时∠AOF度数.参考答案与解析1.A 解析:根据题意得AB =4cm.∵△ABC 是等边三角形,∴AB =BC =4cm ,∠C =60°.当点P 运动5.5秒时,如图所示.则BP =5.5-4=1.5(cm),∴PC =2.5cm.∵∠C =60°,∴∠CPD =30°,∴CD =12CP =54cm.∴PD =CP 2-CD 2=534cm.2.12 解析:根据图像可知点P 在BC 上运动时,此时BP 不断增大,由图像可知:点P 从B 运动到C 的过程中,BP 的最大值为5,即BC =5.点P 运动到点A 时,BP =AB =5.∴△ABC 是等腰三角形.∵M 是曲线部分的最低点,∴此时BP 最小,即BP ⊥AC 时,BP =4,∴由勾股定理得PC =3,∴AC =6,∴△ABC 的面积为12×4×6=12,故答案为12. 3.解:(1)是(2)四边形ABC 1D 1是平行四边形.理由如下:∵∠ABD 1=∠C 1D 1B =60°,∴AB ∥C 1D 1,又∵AB =C 1D 1,∴四边形ABC 1D 1是平行四边形.(3)四边形ABC 1D 1有可能是矩形.此时,∠D 1BC 1=30°,∠D 1C 1B =90°,C 1D 1=1,∴BD 1=2C 1D 1=2.又∵B 1D 1=1,∴BB 1=BD 1-B 1D 1=1,即点B 移动的距离为1.4.(1)证明:当∠AOF =90°时,∠AOF =∠BAC ,∴AB ∥EF .∵AF ∥BE ,∴四边形ABEF 是平行四边形.(2)证明:∵四边形ABCD 是平行四边形,∴AO =CO ,AF ∥EC ,∴∠F AO =∠ECO .在△AOF和△COE 中,⎩⎪⎨⎪⎧∠F AO =∠ECO ,OA =OC ,∠AOF =∠COE ,∴△AOF ≌△COE ,∴AF =CE . (3)解:四边形BEDF 可能是菱形.理由如下:∵△AOF ≌△COE ,∴OE =OF .∵四边形ABCD 是平行四边形,∴OB =OD ,∴EF 与BD 互相平分,∴四边形BEDF 是平行四边形,∴当EF ⊥BD 时,▱BEDF 是菱形.在Rt △ABC 中,AC =(5)2-12=2,∴OA =1=AB .∵AB ⊥AC ,∴∠AOB =45°,∴∠AOF =45°,∴当四边形BEDF 是菱形时,∠AOF =45°.。
微专题:图形变换、动点动态探究问题【河北热点】◆类型一 动点与函数图像的综合问题1.(2017·唐山乐亭县期中)如图①,在等边三角形△ABC 中,点P 以每秒1cm 的速度从点A 出发,沿折线AB →BC 运动,到点C 停止,过点P 作PD ⊥AC ,垂足为D ,PD 的长度y (cm)与点P 的运动时间x (秒)的函数图像如图②所示,当点P 运动5.5秒时,PD 的长是( ) A.534cm B.532cm C .23cmD .33cm2.(2017·河南中考)如图①,点P 从△ABC 的顶点B 出发,沿B →C →A 匀速运动到点A ,图②是点P 运动时,线段BP 的长度y 随时间x 变化的关系图象,其中M 为曲线部分的最低点,则△ABC 的面积是________.◆类型二 特殊四边形中的动态变换问题3.(2017·秦皇岛卢龙县期末)如图①,△ABD 和△BDC 都是边长为1的等边三角形.(1)四边形ABCD ________菱形(填“是”或“不是”);(2)如图②,将△BDC 沿射线BD 方向平移到△B 1D 1C 1的位置,连接BC 1,AD 1,则四边形ABC 1D 1是平行四边形吗?为什么?(3)在△BDC 移动过程中,四边形ABC 1D 1有可能是矩形吗?如果可能,请求出点B 移动的距离(写出过程);如果不可能,请说明理由(图③供操作时使用).4.(2017·定州市期中)如图,平行四边形ABCD 中,AB ⊥AC ,AB =1,BC =5,对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交BC ,AD 于点E ,F .(1)当∠AOF =90°时,求证:四边形ABEF 是平行四边形;(2)试说明在旋转过程中,AF 与CE 总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时∠AOF度数.参考答案与解析1.A 解析:根据题意得AB =4cm.∵△ABC 是等边三角形,∴AB =BC =4cm ,∠C =60°.当点P 运动5.5秒时,如图所示.则BP =5.5-4=1.5(cm),∴PC =2.5cm.∵∠C =60°,∴∠CPD =30°,∴CD =12CP =54cm.∴PD =CP 2-CD 2=534cm.2.12 解析:根据图像可知点P 在BC 上运动时,此时BP 不断增大,由图像可知:点P 从B 运动到C 的过程中,BP 的最大值为5,即BC =5.点P 运动到点A 时,BP =AB =5.∴△ABC 是等腰三角形.∵M 是曲线部分的最低点,∴此时BP 最小,即BP ⊥AC 时,BP =4,∴由勾股定理得PC =3,∴AC =6,∴△ABC 的面积为12×4×6=12,故答案为12. 3.解:(1)是(2)四边形ABC 1D 1是平行四边形.理由如下:∵∠ABD 1=∠C 1D 1B =60°,∴AB ∥C 1D 1,又∵AB =C 1D 1,∴四边形ABC 1D 1是平行四边形.(3)四边形ABC 1D 1有可能是矩形.此时,∠D 1BC 1=30°,∠D 1C 1B =90°,C 1D 1=1,∴BD 1=2C 1D 1=2.又∵B 1D 1=1,∴BB 1=BD 1-B 1D 1=1,即点B 移动的距离为1.4.(1)证明:当∠AOF =90°时,∠AOF =∠BAC ,∴AB ∥EF .∵AF ∥BE ,∴四边形ABEF 是平行四边形.(2)证明:∵四边形ABCD 是平行四边形,∴AO =CO ,AF ∥EC ,∴∠F AO =∠ECO .在△AOF 和△COE 中,⎩⎪⎨⎪⎧∠F AO =∠ECO ,OA =OC ,∠AOF =∠COE ,∴△AOF ≌△COE ,∴AF =CE . (3)解:四边形BEDF 可能是菱形.理由如下:∵△AOF ≌△COE ,∴OE =OF .∵四边形ABCD 是平行四边形,∴OB =OD ,∴EF 与BD 互相平分,∴四边形BEDF 是平行四边形,∴当EF ⊥BD 时,▱BEDF 是菱形.在Rt △ABC 中,AC =(5)2-12=2,∴OA =1=AB .∵AB ⊥AC ,∴∠AOB =45°,∴∠AOF =45°,∴当四边形BEDF 是菱形时,∠AOF =45°.。