选考部分 选修3-4 第十三章 第1单元 光的折射、全反射 知能演练场

高中物理学习材料一、选择题1．光从某种玻璃中射向空气，入射角θ1从零开始增大到某一值的过程中，折射角θ2也随之增大，则下列说法正确的是( )A ．比值θ1/θ2不变B ．比值sin θ1/sin θ2是一个大于1的常数C ．比值sin θ1/sin θ2不变D ．比值sin θ1/sin θ2是一个小于1的常数解析：选CD.光从玻璃射向空气时，玻璃的折射率n ＝sin θ2sin θ1＞1，且不变，因此C 、D正确．2.如图所示为一束光线穿过介质Ⅰ、Ⅱ、Ⅲ时的光路，则( )A ．介质Ⅰ的折射率最大B ．介质Ⅱ的折射率最大C ．介质Ⅲ的折射率最大D ．光在介质Ⅱ中传播速度最大解析：选CD.根据折射情况，Ⅰ与Ⅱ相比，Ⅰ折射率大；Ⅱ与Ⅲ相比，Ⅲ折射率大，所以光的传播速度在Ⅱ中最大，介质Ⅲ的折射率最大．3.一束光从某种介质射入空气中时，入射角θ1＝30°，折射角θ2＝60°，折射光路如图所示，则下列说法正确的是( )A ．此介质折射率为33B ．此介质折射率为 3C ．光在介质中的速度比在空气中小D ．光在介质中的速度比在空气中大解析：选BC.由入射角、折射角及折射定律的含义知n ＝sin θ2sin θ1＝3，故A 错误，B 正确；又由n ＝c v知C 正确D 错误．4．(2012·高考北京卷)一束单色光经由空气射入玻璃，这束光的( ) A ．速度变慢，波长变短 B ．速度不变，波长变短 C ．频率增高，波长变长 D ．频率不变，波长变长解析：选A.玻璃的折射率n ＝c v>1，所以光经空气射入玻璃速度减小．波长、波速和频率三者的关系是v ＝λf ，光经空气进入玻璃，频率f 不变，波长变短，所以A 正确． 5．(2013·余杭实验中学高二月考)单色光在真空中的传播速度为c ，波长为λ0，在水中的传播速度是v ，波长为λ，水对这种单色光的折射率为n .当这束单色光从空气斜射入水中时，入射角为θ1，折射角为θ2，下列说法中正确的是( )A ．v ＝c n ，λ＝λ0c vB ．λ0＝λn ，v ＝c sin θ2sin θ1C ．v ＝cn ，λ＝λ0c vD ．λ0＝λn ，v ＝c sin θ1sin θ2解析：选B.由题意可知，n ＝sin θ1sin θ2，又n ＝cv，所以v ＝c n ＝c sin θ2sin θ1又λ0＝c f，而λ＝v f，所以λ＝v c λ0＝λ0n ，λ0＝n λ＝cvλ.综上所述，只有B 项正确．6．(2013·连云港高二检测)把用相同玻璃制成的厚度为d 的正方体a 和半径亦为d 的半球体b ，分别放在报纸上，且让半球的凸面向上．从正上方分别观察a 、b 中心处报纸上的字，下面的观察记录中正确的是( )A ．a 中的字比b 中的高B ．b 中的字比a 中的高C ．一样高D ．a 中的字较没有玻璃时高，b 中的字和没有玻璃时一样解析：选AD.如图所示，处在半球体b 球心下的字反射的光线经半球体向外传播时，传播方向不变，故人看到字的位置是字的真实位置；而处在正方体a 中心下的字，反射的光线在正方体的上表面处发生折射，折射光线远离法线，当人逆着折射光线看去时，看到的是真实字的虚像，如图中a ′其位置比真实字的位置高，故选AD.7.为了观察门外情况，有人在门上开一小圆孔，将一块圆柱形玻璃嵌入其中，圆柱体轴线与门面垂直，如图所示．从圆柱底面中心看出去，可以看到的门外入射光线与轴线间的最大夹角称为视场角．已知该玻璃的折射率为n ，圆柱长为l ，底面半径r ，则视场角是( )A ．arcsin nlr 2＋l 2 B ．arcsinnrr 2＋l 2 C ．arcsin rr 2＋l 2D ．arcsin lr 2＋l2解析：选 B.光路如图所示，依题意可得：sin θ＝r r 2＋l2，由n ＝sin isin θ得i ＝arcsin(n ·sin θ)＝arcsinnrr 2＋l 2.☆8.如图所示，一束单色光射入一玻璃球体，入射角为60°，已知光线在玻璃球内经一次反射后，再次折射回到空气中时与入射光线平行，此玻璃的折射率为( )A. 2 B ．1.5 C. 3 D ．2解析：选C.作出光在玻璃体内的光路图，如图所示，由几何关系可知，第一次折射时，折射角为30°，则n ＝sin 60°sin 30°＝3，C 项正确．☆9.半径为R的玻璃半圆柱体，截面如图所示，圆心为O，两束平行单色光沿截面射向圆柱面，方向与底面垂直，∠AOB＝60°，若玻璃对此单色光的折射率n＝3，则两条光线经柱面和底面折射后的交点与O点的距离为( )A.R4B.R3C.R2D．R解析：选B.如图所示，光线A 过圆心传播方向不变．光线B 经过柱面时，折射角为θ1，由折射定律得：n ＝sin 60°sin θ1，sin θ1＝1n sin 60°＝12，得θ1＝30°由几何知识可得OE ＝3R3光线BE 从E 点射入空气，折射角θ2＝60° 由几何知识得：OD ＝R3.故选项B 是正确的．二、非选择题 10．某同学在测定一厚度均匀的圆形玻璃的折射率时，先在白纸上作一与圆形玻璃同半径的圆，圆心为O ，将圆形玻璃平放在白纸上，使其边界与所画的圆重合．在玻璃一侧竖直插两枚大头针P 1和P 2，在另一侧再先后插两枚大头针P 3和P 4，使从另一侧隔着玻璃观察时，大头针P 4、P 3和P 2、P 1的像恰在一直线上．移去圆形玻璃和大头针后，在图中画出：(1)沿P 1、P 2连线方向的入射光线通过圆形玻璃后的传播方向； (2)光线在玻璃内的传播方向；(3)过光线的入射点作法线，标出入射角i 和折射角r ； (4)写出计算玻璃折射率的公式．解析：(1)P 1P 2为入射光线，P 3P 4为通过圆形玻璃后的折射光线． (2)O 1O 2光线为入射光线P 1P 2在玻璃中的折射光线． (3)如图所示．(4)n ＝sin i sin r .答案：见解析 11. (2013·烟台二中高二检测)一小孩站在宽6 m 的河边，在他正对面的岸边有一距离河面高度为3 m 的树，树的正下方河底有一块石头，小孩向河面看去，同时看到树顶和石头两者的像且重合．若小孩子的眼睛离河面高为1.5 m ，如图所示，河水的折射率为43，试估算河水深度．解析：光路如图所示，得n ＝sin αsin β，由几何关系得1.5tan α＋3tan α＝6，解得tan α＝43，sin α＝45，P 点至树所在岸边的距离为3tan α＝4 m ，sin β＝442＋h 2，由以上几式解得h ＝5.3 m.答案：5.3 m12．如图所示是一透明的圆柱体的横截面，其半径R ＝20 cm ，折射率为3，AB 是一条直径，今有一束平行光沿AB 方向射向圆柱体，试求：(1)光在圆柱体中的传播速度；(2)距离直线AB 多远的入射光线，折射后恰经过B 点．解析：(1)光在圆柱体中的传播速度v ＝cn＝3×108 m/s. (2)设光线PC 经折射后经过B 点，光路图如图所示由折射定律有：sin αsin β＝n ＝3①又由几何关系有：α＝2β② 解①②得α＝60°光线PC 离直线AB 的距离 CD ＝R sin α＝10 3 cm则距离直线AB 为10 3 cm 的入射光线经折射后能到达B 点．答案：(1)3×108m/s (2)10 3 cm。

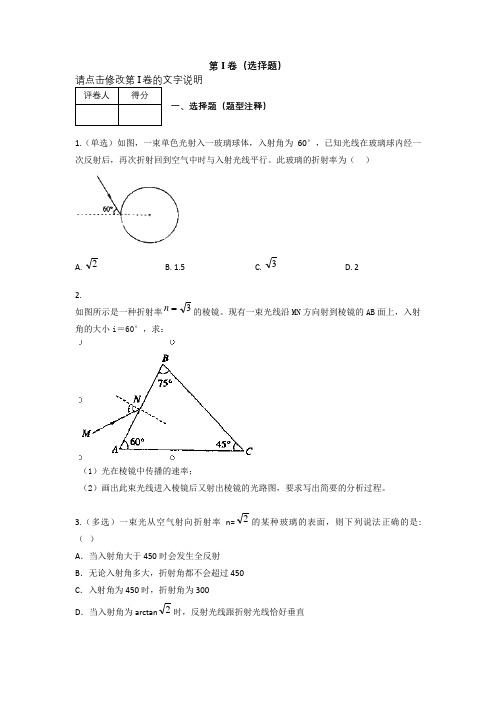
第I卷（选择题）请点击修改第I卷的文字说明评卷人得分一、选择题（题型注释）1.（单选）如图，一束单色光射入一玻璃球体，入射角为60°，已知光线在玻璃球内经一次反射后，再次折射回到空气中时与入射光线平行。

此玻璃的折射率为（）A. 2B. 1.5C. 3D. 22.如图所示是一种折射率3n的棱镜。

现有一束光线沿MN方向射到棱镜的AB面上，入射角的大小i＝60°，求：（1）光在棱镜中传播的速率；（2）画出此束光线进入棱镜后又射出棱镜的光路图，要求写出简要的分析过程。

3.（多选）一束光从空气射向折射率n=2的某种玻璃的表面，则下列说法正确的是:（）A．当入射角大于450时会发生全反射B．无论入射角多大，折射角都不会超过450C．入射角为450时，折射角为300D．当入射角为arctan2时，反射光线跟折射光线恰好垂直第II卷（非选择题）请点击修改第II卷的文字说明评卷人得分二、填空题（题型注释）4.直角玻璃三棱镜的截面如图所示，一条光线从AB面入射，ab为其折射光线，ab与AB 面的夹角α= 60°．已知这种玻璃的折射率n =2，则：①这条光线在AB面上的的入射角为；②图中光线ab （填“能”或“不能”）从AC面折射出去．5.如图所示，一个用透明材料制成的截面为直角三角形的三棱镜ABC．现在有一束单色光从空气中以θ=45°的入射角自直角边AB射入，折射时的偏转角为15°，然后光线射到AC 面而刚好发生了全反射，则这种透明材料的折射率为________，全反射的临界角为_________，角∠A=________.6.如图所示，用某种透光物制成的直角三棱镜ABC；在垂直于AC面的直线MN上插两枚大头针P1、P2，在AB面的左侧透过棱镜观察大头针P1、P2的像，调整视线方向，直到P1的像__________________，再在观察的这一侧先后插上两枚大头针P3、P4，使P3________，P4________.记下P3、P4的位置，移去大头针和三棱镜，过P3、P4的位置作直线与AB面相交于D，量出该直线与AB面的夹角为45°.则该透光物质的折射率n＝________，并在图中画出正确完整的光路图．评卷人得分三、实验题（题型注释）评卷人得分四、计算题（题型注释）7.如图所示，一束光从空气垂直射到直角棱镜的AB面上，已知棱镜材料的折射率为1.4，画出这束光进入棱镜后的光路图（要求必须有计算步骤）8.知光线自空气射入甲介质中，入射角为60°，折射角为30°；光线从乙介质射入空气，入射角为45°，折射角为60°，求：（1）甲、乙两种介质的折射率之比n甲∶n乙；（2）光在甲、乙两种介质中的光速之比v甲∶v乙9.如图所示，真空中有一个半径为R，折射率为n＝2的透明玻璃球．一束光沿与直径成θ0＝45°角的方向从P点射入玻璃球，并从Q点射出，求光线在玻璃球中的传播时间．10.如图所示，真空中有一个半径为R，折射率为n＝2的透明玻璃球．一束光沿与直径成θ0＝45°角的方向从P点射入玻璃球，并从Q点射出，求光线在玻璃球中的传播时间．11.一棱镜的截面为直角三角形ABC ，∠A=30o ，斜边AB=a 。

高中物理选修3---4第十三章《光》全章新课教学课时同步强化训练汇总（附详细参考答案）一、《光的反射和折射》课时同步强化训练（附详细参考答案）二、《全反射》课时同步强化训练（附详细参考答案）三、《光的干涉》课时同步强化训练（附详细参考答案）四、《实验：用双缝干涉测量光的波长》课时同步强化训练（附详细参考答案）五、《光的衍射》《光的偏振》课时同步强化训练（附详细参考答案）六、《光的颜色色散》《激光》课时同步强化训练（附详细参考答案）★★★选修3--4第十三章《光》单元质量检测试卷（一）（附详细参考答案）★★★选修3--4第十三章《光》单元质量检测试卷（二）（附详细参考答案）§§13.1《光的反射和折射》课时同步强化训练班级：_________ 姓名：__________ 成绩：___________ 1.如图所示，光在真空和某介质的界面MN上发生折射，由图可知( )A.光是从真空射入介质的B.C.D.反射光线与折射光线的夹角为60°2.如图所示，虚线表示两种介质的界面及其法线，实线表示一条光线射向界面后发生反射和折射的光线，以下说法正确的是( )A.bO不可能是入射光线B.aO可能是入射光线C.cO可能是入射光线D.Ob可能是反射光线3.关于光的折射现象，下列说法中正确的是( )A.光的传播方向发生改变的现象B.人在岸上观察水中的鱼比实际位置浅C.若光从空气射入某种液体中，它的速率一定减小D.观察者看见太阳刚从地平线升起时，其实太阳位于地平线以下4.用两面平行的玻璃砖测定玻璃的折射率的实验中，已画好玻璃砖界面aa′和bb′，不慎将玻璃砖向上平移了一些，放在如图所示的位置上，而实验中其他操作均正确，测得的折射率将( )A.偏大B.偏小C.不变D.无法确定5.假设地球表面不存在大气层，那么我们观察到的日出时刻与实际存在大气层的情况相比( )A.将提前B.将延后C.不变D.在某些地区将提前，在某些地区将延后6.如图所示，落山的太阳看上去正好在地平线上，但实际上太阳已处于地平线以下，观察者的视觉误差大小取决于当地大气的状况．造成这种现象的原因是( )A.光的反射B.光的折射C.光的直线传播D.小孔成像7.在水中的潜水员斜看岸边的物体时，看到的物体( )A.比物体所处的实际位置高B.比物体所处的实际位置低C.跟物体所处的实际位置一样高D.以上三种情况都有可能8.某研究性学习小组在探究光的折射过程中，研究折射角与入射角之间的关系，当光由空气斜射入玻璃中时，测得实验数据如表：由此实验数据可以初步得到的结论是( )A.在误差允许范围内，入射角与折射角之比总是定值B.在误差允许范围内，入射角正弦与折射角正弦之比总是定值C.在误差允许范围内，入射角与折射角之差总是定值D.在误差允许范围内，入射角正弦与折射角正弦之差总是定值9.在测定玻璃的折射率的实验中，对一块两面平行的玻璃砖，用插针法找出与入射光线对应的出射光线，现在甲、乙、丙、丁四位同学分别做出如图所示的四组插针结果．(1)从图上看，肯定把大头针插错了的同学是_________．(2)从图上看，测量结果准确度最高的同学是_________．10.如图所示，半圆玻璃砖的半径R＝10 cm，折射率为n直径AB与屏幕垂直并接触于A点，激光a以入射角i＝30°射向半圆玻璃砖的圆心O，结果在水平屏幕MN上出现了两个光斑．求两个光斑之间的距离L.11.一个圆柱形筒，直径为12 cm，高16 cm，人眼在筒侧上方某处观察，所见筒侧的深度为9 cm.当筒中盛满液体时，则人眼又恰能看到筒侧的最低点，求：(1)此液体的折射率；(2)光在此液体中的传播速度．§§13.1《光的反射和折射》课时同步强化训练详细参考答案1.【解析】选C.根据图象可知，入射角为30°，折射角为60°，反射光线与折射光线垂直，光是从介质射入真空的，折射率sini sin60n sinr sin30︒=︒＝＝只有C 正确. 2.【解析】选A 、B 、D.由于入射角等于反射角，入射光线、反射光线关于法线对称，所以aO 、Ob 应是入射光线或反射光线,PQ 是法线.又因为反射光线、折射光线都不与入射光线位于法线同侧，所以aO 是入射光线，Ob 是反射光线，Oc 是折射光线.3.【解析】选B 、C 、D.根据光的折射的规律，可知水中的物体视深变浅.光在介质中的传播速率c v n=变小，太阳光的传播方向发生弯曲，故B 、C 、D 对；光发生反射时传播方向也发生改变，故A 错.4.【解析】选C.经过玻璃砖的光路如题图中实线所示，由于所作的玻璃砖分界线不是实际的分界线，如图中虚线所示，由几何知识可知，测出的折射角与正确值相同．5.【解析】选B.如果不存在大气层，只有当太阳上升到观察者的“地平线”时才能被观察到.6.【解析】选B.太阳光线进入大气层发生折射，使传播方向改变，使人感觉太阳的位置比实际位置偏高，故B 正确.7.【解析】选A.当从水中确定空气中物体的位置时，潜水员会感觉到岸上物体的位置升高，故A 项正确．【变式备选】把用相同玻璃制成的厚度为d的正方体a和半径亦为d 的半球体b，分别放在报纸上，且让半球的凸面向上．从正上方分别观察a、b中心处报纸上的字，下面的观察记录中正确的是( )A.a中的字比b中的字高B.b中的字比a中的字高C.一样高D.a中的字较没有玻璃时的高，b中的字和没有玻璃时的一样【解析】选A、D.如图所示，放在b中的字反射的光线经半球体向外传播时，传播方向不变，故人看到字的位置是字的真实位置．而放在a中的字经折射，人看到的位置比真实位置要高．8.【解析】选B.由表中数据可得，在误差允许范围内，入射角正弦与折射角正弦之比总是定值.故B对.9.【解析】光线透过平行玻璃砖时出射光线与入射光线平行，且从空气射入玻璃砖时入射角大于折射角，因而光线透出时，相对于入射光线向右下侧发生偏移.另外，插针确定光路时，入射角稍大些好且插针相距稍远些好．由上图可知，甲、乙图中出射光线向左上侧偏移，不符合事实，肯定插错了.丙与丁相比较，前者入射角及插针间距都比丁图小些，故丁同学测量最准确．答案：(1)甲、乙(2)丁10.【解析】画出光路图，设折射角为γ， 根据折射定律sin n siniγ＝，解得γ＝60°，由几何知识得，△OPQ 为直角三角形，所以两个光斑PQ 之间的距离L ＝PA ＋AQ ＝Rtan30°+2Rsin60°解得L 23.1 cm ≈ 答案：23.1 cm【总结提升】折射问题的四点注意(1)根据题意画出正确的光路图；(2)利用几何关系确定光路中的边、角关系,要注意入射角、折射角的确定；(3)利用反射定律、折射定律求解；(4)注意光路可逆性、对称性的应用．11.【解题指南】画光路图时应注意的问题：(1)光路是可逆的．(2)垂直界面入射的光线，折射光线与入射光线在同一直线上．【解析】先画出一圆柱形筒，筒高为H ＝16 cm ，直径d ＝12 cm.人眼在A 处，筒侧底部“最低点”为B ，筒内无液体时，人眼能见深度h＝9 cm.筒内盛满液体时，人眼看到B 点．根据光的折射定律画出光路如图所示．(1)1sin θ2sin θ 此液体的折射率12sin n sin θθ＝ 43＝ (2)光在此液体中的传播速度8c v 2.2510 m /s n ⨯＝＝答案：(1)43(2)2.25³108 m/s§§13.2《全反射》课时同步强化训练班级：_________ 姓名：__________ 成绩：___________ 1．光纤通信是一种现代通信手段，它可以提供大容量、高速度、高质量的通信服务.目前，我国正在大力建设高质量的宽带光纤通信网络．下列说法正确的是( )A．光纤通信是利用光作为载体来传递信息B．光导纤维传递光信号是利用光的直线传播的原理C．光导纤维传递光信号是利用光的折射原理D．目前广泛应用的光导纤维是一种非常细的特制玻璃丝2．一束光线从折射率为1.5的玻璃内射向空气，在界面上的入射角为45°.如图所示的四个光路图中正确的是( )3．如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射向E点，并偏折到F点．已知入射方向与边AB的夹角为θ=30°，E、F分别为边AB、BC的中点，则( )AB．光在F点发生全反射C．光从空气进入棱镜，波长变小D．从F点出射的光束与入射到E点的光束平行4.如图所示，一束激光从O点由空气射入厚度均匀的介质，经下表面反射后，从上表面的A点射出.已知入射角为i ,A与O 相距l,介质的折射率为n,试求介质的厚度d.5．如图所示，空气中有一横截面为半圆环的均匀透明柱体，其内圆半径为r，外圆半径为R，现有一束单色光垂直于水平端面A 射入透明柱体，只经过两次全反射就垂直于水平端面B射出．设透明柱体的折射率为n，光在透明柱体内传播的时间为t，若真空中的光速为c，则( )A．n B．n可能为2C．t可能为c D．t可能为4.8rc6．如图是一个14圆柱体棱镜的截面图，图中E、F、G、H将半径OM 分成5等份，虚线EE1、FF1、GG1、HH1平行于半径ON，ON边可吸收到达其上的所有光线．已知该棱镜的折射率n=53，若平行光束垂直入射并覆盖OM，则光线( )A．不能从圆弧NF1射出B．只能从圆弧NG1射出C．能从圆弧G1H1射出D．能从圆弧H1M射出7.如图所示，一束平行光从真空垂直射向一块半圆形玻璃砖的底面，下列说法正确的是( )A.只有圆心两侧一定范围内的光线不能通过玻璃砖B.只有圆心两侧一定范围内的光线能通过玻璃砖C.通过圆心的光线将沿直线穿过，不发生偏折D.圆心两侧一定范围外的光线将在曲面处发生全反射8．在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴(图中虚线)与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为1.5，则光束在桌面上形成的光斑半径为( )A．r B．1.5r C．2r D．2.5r 9.2008年奥运会会上，光纤通信网覆盖了所有的比赛场馆，为各项比赛提供安全、可靠的通信服务，光纤通信是利用光的全反射将大量信息高速传输．如图是一根长为l的光导纤维，由内芯和包层两层介质组成，其折射率分别为n1和n2，则n1____________________n2(选填“<”、“>”或“=”)；若发生全反射的临界角为θ，光在真空中的速度为c，则一束光从它的一个端面射入，又从另一端面射出所需的最长时间为__________．10．一束单色光由左侧射入盛有清水的薄壁圆柱形玻璃杯，如图所示为过轴线的截面图，调整入射角α，使光线恰好在水和空气的界面上，求sinα的值．发生全反射．已知水的折射率为4311.如图所示，扇形AOB为透明柱状介质的横截面，圆心角∠AOB=60°.一束平行于角平分线OM的单色光由OA射入介质，经OA折射的光线恰平行于OB.（1）求介质的折射率.（2）折射光线中恰好射到M点的光线___________(选填“能”或“不能”）发生全反射.§§13.2《全反射》课时同步强化训练详细参考答案1．【解析】选A 、D.光导纤维是一种非常细的特制玻璃丝，直径只有几微米到一百微米，由内芯和外套组成，内芯的折射率大，其原理是光传播时在两个界面处发生全反射，故D 对，B 、C 错．光是一种电磁波，它像无线电波一样，作为一种载体来传递信息，A 对． 2．【解析】选A.设临界角为C ，则sinC=1n=0.67，sin45°，入射角45°大于临界角C ，发生全反射，故正确选项为A.3．【解析】选A 、C.本题考查折射率和全反射的有关知识，意在考查学生运用几何光学知识解决问题的能力．由几何知识可知三角形EBF 为等边三角形，故从E 点入射的光线，入射角为60°，折射角为30°，由折射定律可知sin60n sin30︒==︒，A 正确；光射在F 点时，入射角为30°，故不发生全反射，折射角为60°，B 、D 错；光从空气中进入棱镜中，光速减小，而光的频率不变，所以光在棱镜中的波长变小，C 正确． 4.【解析】设折射角为r ，由折射定律sinin sinr=和几何关系l =2dtanr ，联立可解得厚度d .=5．【解题指南】解答本题应把握以下两点：（1）作出光路图，由临界角的范围求出折射率. （2）由n=cv 和t=x v分析时间的取值范围.【解析】选A 、B.根据题意可画出光路图如图所示，则两次全反射时的入射角均为45°，所以全反射的临界角C ≤45°，折射率n ≥1sin45 A 、B 项均正确；光在介质中的传播速度v=c n ，所以传播时间t=x v ≥c，C 、D 项均错误．6．【解析】选B.由折射率n=53知该棱镜的全反射临界角为C=37°(sinC=35)，刚好从G 点入射的光线垂直进入棱镜后，在G 1点恰好发生全反射，则 1G M 圆弧上所有入射光线均发生全反射，不会从中射出，只有 1NG 圆弧上入射的光线折射后射出棱镜．所以只有B 正确，A 、C 、D 错误．7.【解析】选B 、C 、D.垂直射向界面的光线不发生偏折，因而光束沿直线平行射到半圆面上，其中通过圆心的光线将沿直线穿过，不发生偏折；由中心向两侧，光从半圆面进入真空时的入射角逐渐增大并趋于90°，当入射角等于或大于临界角时，会发生全反射，故B 、C 、D 正确.8．【解析】选C.如图所示，光线射到A 或B 时，入射角大于临界角，发生全反射，而后由几何关系得到第二次到达界面的时候垂直射出．O点为△ABC 的重心，设EC=x ，则由几何关系得到：x 2x r 3=.解得光斑半径x=2r.9.【解析】光从内芯射向包层时会发生全反射，故内芯的折射率应大于包层的折射率；当内芯射向包层的入射光的入射角等于临界角θ时，光的路线最长，所用时间也最长，设为t max ，此时光束在沿光导纤维方向的速度分量为vsin θ，则光在穿过光导纤维时有l =vsin θ²t max ， 得1max 1n t .csin vsin csin n ===θθθl l l答案：>1n csin θl10．【解析】当光线在水面发生全反射时，有 sinC=1n① 当光线从左侧射入时，由折射定律有sin n sin C 2α=π-（）② 联立①②式，代入数据可得sin α=3.答案：3【变式备选】一束光波以45°的入射角，从AB 面射入如图所示的透明三棱镜中，棱镜折射率试求光进入AB面的折射角，并在图上画出该光束在棱镜中的光路．【解析】sin α=sini 1n 2==，α=30°由1sinC n2==得，C=45°. 光在AC 面发生全反射，并垂直BC 面射出． 答案：30° 光路图如图11.【解析】（1）由题意画出光路图如图所示，可得入射角i=60°，折射角r=30°，由折射定律可得此介质的折射率为sini sin60n sinr sin30︒===︒（2）由题意画出恰好经过M 点的折射光线如图所示，可得出此时射向M 点的入射角为30°，全反射的临界角11sinC sin30n 2==>︒=，故不能发生全反射.答案：（1）（2）不能【总结提升】应用光的折射和全反射理论分析问题 （1）正确、灵活地理解、应用折射率公式 折射率公式为sinin sinr=（i 为真空中的入射角，r 为某介质中的折射角）.根据光路可逆原理，入射角、折射角是可以随光路的逆向而“换位”的.我们可以这样来理解、记忆：sini n sinr =（空）（介）或1sini n sinr =（介）（空）. （2）对临界角的理解光线从介质进入真空或空气.折射角r=90°时，发生全反射，此时的入射角i （介）叫临界角C. 由1sini sinC nsinr ==（介）（空）.（3）分析、计算问题的应用分析、计算时要掌握好n 的两种表达式及有关数学知识，如三角函数（尤其是特殊角的函数）.着重理解两点：第一，光的频率（颜色）由光源决定，与介质无关；第二，同一介质中，频率越大的光折射率越大.例如同一介质对紫光的折射率大，对红光的折射率小.再应用n=c v等知识，就能准确而迅速地判断有关色光在介质中的传播速度、波长、入射光线与折射光线偏折程度等问题.§§13.3《光的干涉》课时同步强化训练班级：_________ 姓名：__________ 成绩：___________1．由两个不同光源所发出的两束白光落在同一0点上，不会产生干涉现象．这是因为( )A．两个光源发出光的频率相同B．两个光源发出光的强度不同C．两个光源的光速不同D．这两个光源是彼此独立的，不是相干光源2．从两只相同的手电筒射出的光，当它们在某一区域叠加后，看不到干涉图样，这是因为( )A．手电筒射出的光不是单色光B．干涉图样太细小看不清楚C．周围环境的光太强D．这两束光为非相干光源3．两盏普通白炽灯发出的光相遇时，我们观察不到干涉条纹，这是因为( )A．两盏灯亮度不同B．灯光的波长太短C．两灯光的振动情况不同D．电灯发出的光不稳定4．用红光做双缝干涉实验，在屏上观察到干涉条纹．在其他条件不变的情况下，改用紫光做实验，则干涉条纹间距将变__________，如果改用白光做实验，在屏上将出现__________色条纹．5.能发生干涉的两束光应是( )A.亮度一样B.颜色一样C.频率相等D.传播方向相同6．如图所示是单色光双缝干涉实验某一时刻的波形图，实线表示波峰，虚线表示波谷．在此时刻，介质中A点为波峰相叠加点，B点为波谷相叠加点，A、B连线上的C点为某中间状态相叠加点．如果把屏分别放在A、B、C三个位置，那么( )A．A、B、C三个位置都出现亮条纹B．B位置出现暗条纹C．C位置出现亮条纹或暗条纹要由其他条件决定D．以上结论都不对7．取两块平板玻璃，合在一起用手捏紧，会从玻璃板上看到彩色条纹，这是光的干涉现象，有关这一现象的叙述正确的是( ) A．这是上下两块玻璃板的上表面反射光干涉的结果B．这是两玻璃板间的空气薄层上下两表面的反射光干涉的结果C．这是上面一块玻璃的上、下两表面的反射光干涉的结果D．这是下面一块玻璃的上、下两表面的反射光干涉的结果8．杨氏双缝干涉实验中，下列说法正确的是(n为自然数，λ为光波波长)( )①在距双缝的路程相等的点形成暗条纹；②在距双缝的路程差为nλ的点形成亮条纹；④在的点形成亮条纹；③在距双缝的路程差为n2距双缝的路程差为（n＋1）λ的点形成暗条纹．2A．①②B．②③C．③④D．②④9．用波长为λ的平行单色光做“双缝干涉”实验，O点处为中央亮条纹，若要O点处为中央亮条纹上面的第一条亮条纹，则双缝应向_______移动_______．(双缝间距为d，挡板与屏间距离为l)10.如图所示，用激光束照射双缝干涉实验装置，后面屏上出现干涉条纹.其中单缝的作用是产生线光源，单缝、双缝应平行放置.若将单缝绕中心轴旋转（不超过90°）,条纹将发生什么变化？若将双缝绕中心轴旋转（不超过90°）,条纹将发生什么变化？11．光纤通信是70年代以后发展起来的新兴技术，世界上许多国家都在积极研究和发展这种技术．发射导弹时，可在导弹后面连一根细如蛛丝的光纤，就像放风筝一样，这种纤细的光纤在导弹和发射装置之间，起着双向传输信号的作用．光纤制导的下行光信号是镓铝砷激光器发出的在纤芯中波长为0.85 μm的单色光．上行光信号是铟镓砷磷发光二极管发射的在纤芯中波长为1.06 μm 的单色光．这种操纵系统通过这根光纤向导弹发出控制指令，导弹就如同长“眼睛”一样盯住目标．根据以上信息，回答下列问题：(1)在光纤制导中，上行光信号在真空中波长是多少？(2)为什么上行光信号和下行光信号要采用两种不同频率的光？(已知光纤纤芯的折射率为1.47)§§13.3《光的干涉》课时同步强化训练详细参考答案1．【解析】选D.紧扣相干光源的条件须为同频率的单色光源，而不同光源发出的光频率一般不同，所以不会产生干涉现象．2．【解析】选D.两束光的频率不同，不满足干涉产生的条件．3．【解析】选C.一般情况下，两个不同的光源发出的光或同一个光源的不同部分发出的光振动情况往往是不同的，由点光源发出的光或同一列光分出的两列光其振动情况是相同的．4．【解析】在双缝干涉实验中，在其他条件不变的情况下，干涉条纹的间距与入射光的波长成正比，紫光波长小于红光波长，所以改用紫光做实验，干涉条纹间距将变小．改用白光做实验时，由于七色光的波长不同，各自干涉条纹的间距不同．在光屏幕上单色光加强的位置不同，于是出现彩色干涉条纹．可通过实验现象直接得出答案．答案：小彩5.【解析】选C.发生干涉的条件是两光源的频率相同，振动方向相同，相位差恒定.6．【解题指南】（1）在干涉现象中，所谓“振动加强的点”是指两列波在该点引起的振动方向总是相同，该点的振幅是两列波的振幅之和，而不要理解为该点始终处于波峰或波谷，在某些时刻它也可以位于平衡位置(如图中C点)．（2）所谓“振动减弱的点”是指两列波在该点引起的振动方向总是相反的，该点的振幅是两列波的振幅之差，如果两列波的振幅相同，则该点始终在平衡位置，对光波而言，该点是完全暗的．【解析】选A.本题中，A、B、C三点总是振动加强的点，屏上对应出现的都是亮条纹．另外，要特别注意波谷与波谷相遇的点(图中B点)振动也是加强的，不要以为B点是暗的．7．【解析】选B.形成干涉条纹是有一定条件的，即两列相干光的路程差需要连续变化，当Δr＝±kλ(k＝0,1,2…)时，形成明条纹，当λ(k＝0,1,2…)时，形成暗条纹．当入射光是白光时，Δr＝±(2k＋1)2就会形成彩色条纹，对平板玻璃来说，每一块平板玻璃上下表面都是平行的，故不具备产生干涉条纹的条件，而中间的空气膜，则可能具备这一条件．8．【解析】选D.在双缝干涉实验中，当某处距双缝距离之差Δx为波长的整数倍时，即Δx＝kλ，k＝0,1,2,3…这点为加强点，该处出现亮条纹；当某处距双缝距离之差Δx为半波长的奇数倍时，即Δx＝λ，k＝0,1,2,3…这点为减弱点，该处出现暗条纹．(2k＋1)2【总结提升】光的干涉条件的分析生活中任何两个各自独立发光的光源产生的光在空间相叠加都不会产生干涉，这是由物体的发光机理决定的，即任何两个各自独立的光源都不是相干光源.所以杨氏双缝干涉中单缝的作用就是从同一光源得到线光源，以便能有相同的频率和振动规律.双缝是由同一个狭缝照亮的，所以双缝也就成了一对相干光源.光的相干条件中频率相同是光发生干涉的必要条件，要发生干涉，两光源还必须具有相同的振动方向和恒定相位差.通常的问题中对相干光源的条件说法比较含蓄，要注意挖掘.9．【解析】当下移Δx＝dlλ时，开始的下边第一条亮条纹后来刚好是中央亮条纹，那么开始的中央亮条纹处刚好是上面第一条亮条纹．答案：下dlλ10.【解析】在双缝干涉实验中，单缝的作用是形成线光源，双缝的作用是形成振动情况相同的相干光源.当单缝旋转时，双缝被照亮的面积减小，双缝虽然仍能形成相干光源，但由于通过双缝的光能量减少，所以屏上仍能产生干涉条纹，但条纹变暗.当双缝旋转时，同样会导致干涉条纹变暗.同时，干涉条纹保持与双缝平行，也随双缝的旋转而旋转.答案：见解析11．【解析】(1)设信号频率为f，真空中的波长为λ0，c＝λ0f，光在纤芯中的频率仍为f，波长为λ，则光在纤芯中的速度v＝λf，又n＝cv ，可以得出：n1.471.06m1.56m.λλ⨯μμ＝＝＝(2)上行光信号和下行光信号的频率相同，将发生干涉现象而互相干扰．答案：（1）1.56 μm （2）见解析§§13.4《实验：用双缝干涉测量光的波长》课时同步强化训练班级：_________ 姓名：__________ 成绩：___________1．分别使红光和紫光先后用同一装置进行双缝干涉实验，在屏上得到相邻的条纹间的距离分别为Δx1和Δx2，则( )A．Δx1＜Δx2B．Δx1＞Δx2C．若双缝间距d减小，而其他条件保持不变，则Δx1增大D．若双缝间距d减小，而其他条件保持不变，则Δx1不变2．用单色光做双缝干涉实验，下述说法正确的是( )A．相邻干涉条纹之间的距离相等B．中央明条纹宽度是两边明条纹宽度的2倍C．屏与双缝之间距离减小，则屏上条纹间的距离增大D．在实验装置不变的情况下，红光的条纹间距小于蓝光的条纹间距3．某同学按实验装置安装好仪器后，观察光的干涉现象，获得成功，若他在此基础上对仪器的安装做如下改动，仍能使实验成功的是( )A．将遮光筒内的光屏，向靠近双缝的方向移动少许，其他不动B．将滤光片移至单缝和双缝之间，其他不动C．将单缝向双缝移动少许，其他不动D．将单缝与双缝的位置互换，其他不动4.在“用双缝干涉测光的波长”的实验中，调节分划板的位置，使分划板中心刻线对齐某亮条纹的中心，测量如图所示，此时螺旋测微器。

高中物理第十三章光第2节全反射课后训练新人教版选修3-4 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中物理第十三章光第2节全反射课后训练新人教版选修3-4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中物理第十三章光第2节全反射课后训练新人教版选修3-4的全部内容。

全反射1．如下各图画的是光由空气进入全反射（等腰直角）玻璃棱镜，再由棱镜射入空气中的光路图。

其中正确的光路图是( ）2．如图，一个三棱镜的截面为等腰直角△ABC ，∠A 为直角.此截面所在平面内的光线沿平行于BC 边的方向射到AB 边，进入棱镜后直接射到AC 边上,并刚好能发生全反射。

则该棱镜材料的折射率为( ）A ．2 C ．32D ． 3．如图所示，ABCD 是两面平行的透明玻璃砖，AB 面和CD 面平行，它们分别是玻璃和空气的界面，设为界面Ⅰ和界面Ⅱ，光线从界面Ⅰ射入玻璃砖，再从界面Ⅱ射出，回到空气中，如果改变光到达界面Ⅰ时的入射角，则（ )A ．只要入射角足够大，光线在界面Ⅰ上可能发生全反射现象B ．只要入射角足够大，光线在界面Ⅱ上可能发生全反射现象C ．不管入射角多大，光线在界面Ⅰ上都不可能发生全反射现象D ．不管入射角多大,光线在界面Ⅱ上都不可能发生全反射现象4．光纤电缆是20世纪最重要的发明之一。

发明光纤电缆的就是被誉为“光纤之父"的华人科学家高锟。

2008年奥运会上，光纤通信网覆盖所有的奥运场馆，为各项比赛提供安全、可靠的通信服务，光纤通信是利用光的全反射将大量信息高速传输。

若采用的光导纤维是由内芯和包层两层介质组成,下列说法正确的是（ ）A ．内芯和包层折射率相同，折射率都大B ．内芯和包层折射率相同，折射率都小C ．内芯和包层折射率不同，包层折射率较大D ．内芯和包层折射率不同,包层折射率较小5．如图所示，有一束平行于等边三棱镜截面ABC 的单色光从空气射向E 点，并偏折到F 点，已知入射方向与边AB 的夹角为θ＝30°,E 、F 分别为边AB 、BC 的中点，则( )A B ．光在F 点发生全反射C ．光从空气进入棱镜，波长变小D ．从F 点出射的光束与入射到E 点的光束平行 6．已知介质对某单色光的临界角为C ,则( )A ．该介质对这种单色光的折射率等于1sin CB ．此单色光在该介质中的传播速度等于c ·sinC (c 是光在真空中的传播速度） C ．此单色光在该介质中的传播波长是在真空中波长的sin CD ．此单色光在该介质中的频率是在真空中的1sin C倍7．如图所示，直角玻璃棱镜中∠A ＝70°,入射光线垂直于AC 面，求光线从棱镜第一次射入空气时的折射角，并作光路图..8．一玻璃立方体中心有一点状光源。

高中物理第十三章光2 全反射课后训练新人教版选修3-4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中物理第十三章光2 全反射课后训练新人教版选修3-4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中物理第十三章光2 全反射课后训练新人教版选修3-4的全部内容。

全反射基础巩固1，一束光从该介质射向空气，入射角是60°，则下列光路图中正确的是（图中Ⅰ为空气,Ⅱ为介质)（）甲2．空气中两条光线a和b从方框左侧入射，分别从方框下方和上方射出,其框外光线如图甲所示。

方框内有两个折射率n＝1。

5的玻璃全反射棱镜。

图乙给出了两棱镜四种放置方式的示意图，其中能产生图甲效果的是（)乙3．光导纤维是利用光的全反射来传输光信号的。

如图所示,一光导纤维内芯折射率为n1，外层折射率为n2，一束光信号与界面夹角为α由内芯射向外层，要在界面上发生全反射，必须满足的条件是( )A．n1＞n2，α小于某一值B．n1＜n2，α大于某一值C．n1＞n2，α大于某一值D．n1＜n2，α小于某一值4．下列说法正确的是( ）A．潜在水中的潜水员斜向上看岸边的物体时，看到的物体的像将比物体所处的实际位置低B．光纤通信是一种现代通信手段，它是利用光的全反射原理来传播信息的C．玻璃杯裂缝处在光的照射下，看上去比周围明显亮，是由于光的全反射D．海市蜃楼产生的原因是由于海面上上层空气折射率比下层空气折射率大能力提升5．如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射向E点，并偏折到F 点.已知入射方向与边AB的夹角为θ＝30°，E、F分别为边BC的中点，则( ）AB ．光在F 点发生全反射C ．光从空气进入棱镜，光速变小D ．从F 点出射的光束与入射到E 点的光束平行6．如图，一个三棱镜的截面为等腰直角△ABC ，∠A 为直角。

光的反射和折射1．(多选）（2018·西南大学附中高二下学期检测）根据图中的漫画，判断下列说法中正确的是（BD )A．人看到的是鱼的实像，位置变浅了些B．人看到的是鱼的虚像，位置变浅了些C．鱼看到的是人的实像,位置偏低了些D．鱼看到的是人的虚像，位置偏高了些解析：人看鱼的光路如图甲所示，因入射角i小于折射角r，则人将看到鱼的虚像,且位置比实际情况变浅了些，B正确；鱼看到人的光路如图乙所示，因入射角i大于折射角r，则鱼将看到人的虚像，且比实际位置要高，D正确。

2．(2019·吉林省延边二中高二下学期期中)一束光由空气射入某介质，当入射光线和界面的夹角为30°时，折射光线恰好与反射光线垂直，则光在该介质中的传播速度是（ D ）A。

错误!B．错误!C.错误!c D．错误!c解析：光路如图所示。

根据折射定律得介质的折射率n＝错误!＝错误!，由n＝错误!得光在介质中的传播速度v＝错误!＝错误!c。

故选D。

3．（2019·山东省烟台市高三模拟）如图所示的装置可以测量棱镜的折射率。

ABC表示待测直角棱镜的横截面，棱镜的顶角为α,紧贴直角边AC放置一块平面镜。

一光线SO射到棱镜的AB面上，适当调整SO的方向，当SO与AB成β角时,从AB面射出的光线与SO重合。

（1）画出光线SO进入棱镜的折射光线；（2）求出棱镜的折射率n。

答案：(1)见解析图（2)n＝错误!解析:(1）光路如图所示.（2）入射角i＝90°－β要使从AB面射出的光线与SO重合,则AB面上折射光线必须与AC面垂直，由几何知识得到，折射角r＝α由折射定律得：n＝错误!。

尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

主动成长夯基达标1.关于光的反射与折射，以下说法正确的是（ ）A.光发生反射时，光的传播方向一定改变B.光发生反射时，光的传播方向可能偏转90°C.光发生折射时，一定伴随着反射现象D.光发生反射时，一定伴随着折射现象 思路解析：光发生反射时，光的传播方向一定改变，有人认为当入射角为0°时，也就是光线垂直界面入射时，反射角为零，光线不改变方向，实际上光的传播方向改变180°，选项A 正确. 当入射角为45°时，反射角也为45°，光的传播方向偏转90°，选项B 正确.光发生折射时，一定伴随着反射现象，而当发生全反射现象时，只有反射现象而无折射现象. 答案：ABC2.一束光线与水平方向成30°，从空气射入水中，其反射光线和折射光线恰好垂直，则反射角和折射角各为（ ） A.30° 30° B.60° 60° C.60° 30° D.30° 60° 思路解析：我们可以根据题意画一简单的光路图，根据题中条件可知入射角为60°，则反射角为60°，由反射光线和折射光线的垂直关系可知折射角为30°. 答案：C3.光在某种玻璃中的速度是3×108 m/s ，若使光由空气射入这种玻璃，且使折射光线与反射光线垂直，则入射角应是（ ） A.30° B.60° C.45° D.90°思路解析：由光在玻璃中传播速度可知：玻璃对这种光的折射率.310310388=⨯⨯==v c n 画光路图如图14所示.设入射角为θ，折射角为r ，则,3sin sin ==n rθ又θ+r=90°，则θ=60°.图14答案：B4.光从某介质射入空气，入射角θ1从零开始增大到某一值的过程中，折射角θ2也随之增大，则下列说法中正确的是（ ）A.比值θ1/θ2不变B.比值sinθ1/sinθ2不变C.比值sinθ1/sinθ2是一个大于1的常数D.比值sinθ1/sinθ2是一个小于1的常数 思路解析：由折射率概念可知：折射率与介质有关，对于同一束光介质的折射率不变，即21sin sin θθ=n 不变，又vcn =,故n 始终大于1. 答案：BC5.已知水的折射率为1.33,一潜水员自水下目测到立于船头的观察者距水面的距离为h 1，而船头的观察者目测潜水员距水面深h 2，则（ ）A.潜水员的实际深度大于h 2，观察者实际高度大于h 1B.潜水员的实际深度小于h 2，观察者实际高度小于h 1C.潜水员的实际深度大于h 2，观察者实际高度小于h 1D.潜水员的实际深度小于h 2，观察者实际高度大于h 1 思路解析：设观察者实际高底为H ，则h 1=nH,n h H 1=;设潜水员实际深度为H′,则nH h '=2，故正确选项为C.答案：C6.如图13-1-5所示，有玻璃三棱镜ABC ，顶角A 为30°，一束光线垂直于AB 射入棱镜，由AC 射出进入空气，测得出射光线与入射光线间夹角为30°.则棱镜的折射率为（ ）图13-1-5A.21B.22C.3D.33思路解析：光的传播光路图如图15所示，∠A=30°，则入射角∠MON=30°，由题意∠GOF=30°，且∠EOF=30°.故折射角∠EOG=60°，故折射率2sin sin =∠∠=MONEOGn .图15答案：C7.如图13-1-6所示，为了观察门外情况，有人在门上开一个圆孔，将一块圆柱形玻璃嵌入其中，圆柱体轴线与门面垂直.从圆柱底面中心看出去，可以看到的门外入射光线与轴线间的最大夹角称作视场角.已知该玻璃的折射率为n ，圆柱体长为l ，底面半径为r ，则视场角是（ ）图13-1-6A.22arcsin l r nl + B.22arcsin l r nr + C.22arcsinlr n r+ D.22arcsinlr n l+思路解析：如图16所示，设最大视场角为α,据折射定律：图16θαsin sin =n ,其中sinθ=22l r r +解得22arcsin l r nr+=α答案：B8.如图13-1-7所示，光线以入射角θ从空气射向折射率2=n 的透明介质表面，则当入射角为45°时，反射光线与折射光线的夹角为___________.图13-1-7思路解析：当入射角为45°时，可由折射定律算出其折射角为30°，故反射光线与折射光线间的夹角为180°-45°-30°=105°. 答案：105°9.如图13-1-8所示，一根竖直插入水中的杆AB ，在水中部分长1.0 m ，露出水面部分长0.3 m ，已知水的折射率为34.则当阳光与水平面成37°角时，杆AB 在水下的影长为_________ m.图13-1-8思路解析：杆在水中的折射光路图如图17所示，由题意知：入射角θ=53°,设折射角为r,则34sin sin ==r n θ得sinr=0.6,tanr=43图17故杆的影长BD=m r CB AC r CB CO )431343.0(tan 37cot tan ⨯+⨯=∙+∙=∙+︒=1.15 m. 答案：1.1510.光线以60°的入射角从空气射入玻璃中，折射光线与反射光线恰好垂直.（真空中的光速c=3.0×108 m/s ） （1）画出折射光路图；（2）求出玻璃的折射率和光在玻璃中的传播速度； （3）当入射角变为45°时，折射角等于多大？（4）当入射角增大或减小时，玻璃的折射率是否变化？说明理由. 解：（1）光路图如图18所示，其中AO 为入射光线，BO 为折射光线.（2）由题意，rn sin sin θ=,又θ+r=90°,得n=3. 设水中光速为v,由折射定律vcn =得图18v=3×108m/s.(3)当入射角为45°,介质折射率不变：r n sin sin θ=得345sin sin sin ︒==n r θ得.66arcsin=r (4)不变化，折射率是由介质和入射光共同决定的物理量，与入射角大小无关. 答案：（1）如解析图 （2）3 3×108 m/s（3）66arcsin(4)不变，理由略 11.如图13-1-9所示，水面上漂浮着一半径为r 的圆形薄木板，在木板圆心的正上方距木板高度h 的A 处有一个点光源S.由于木板的影响，点光源发出的光线射入水中后，在水底平面上形成一圆形阴影.已知水深为H ，水的折射率为n ，求阴影的半径.图13-1-9解：如图19所示，由折射定律可得n =21sin sin θθ ①图19sinθ1=22rh r + ②因为x=Htanθ2=22222sin 1sin cos sin θθθθ-=H H所以222222222212212121)(sin sin sin 1sin rn r h Hr r h r n r h r Hn H n n H x -+=+-+=-=-=θθθθ所以.)1(2222-++=n r h n rHr R答案：)1(2222-++=n r h n rHr R走近高考12.如图13-1-10所示，一束平行单色光的宽度为d ，由空气射入某液体中，入射角为45°，已知该液体的折射率为2，则光束在液体中传播时的宽度d′=_________.图13-1-10 思路解析：光束传播的光路图如图20所示，设折射角为r,图20由折射定律：n r=sin sin θ,将θ=45°，2=n 代入得r=30°. 由图知：OO′=θsin d ,同理d′=OO′·cosr=θsin d·cosr=d·cos30°/cos45°=.26d 答案：d 26 13.如图13-1-11所示，光线以入射角θ1从空气射向折射率2=n 的玻璃表面.图13-1-11（1）当入射角θ1=45°时，反射光线与折射光线间的增值角θ为多少？ （2）当入射角θ1为多少时，反射光线和折射光线垂直？解：设折射角为θ2，由21sin sin θθ=n ,sinθ2=21245sin sin 1==︒n θ 所以θ2=30°又θ1′=45°,则反射光线与折射光线的增值角θ=180°-θ1′-θ2=105°. (2)当反射光线和折射光线垂直时， θ1′+θ2′=90°11121tan cos sin sin sin θθθθθ===n 则入射角.2arctan 1=θ 答案：（1）105° (2)arctan2.14.如图13-1-12所示，游泳池宽度L=15 m ，水面离岸边的高度为0.5 m ，在左岸边一标杆上装有一A 灯，A 灯距地面高0.5 m ，在右岸边站着一个人，E 点为人眼的位置，人眼距地面高1.5 m.若此人发现A 灯光经水面反射所成的像与左岸水面下某处的B 灯光经折射后所成的像重合，已知水的折射率为1.3，则B 灯在水面下多深处？（B 灯在图中未画出）图13-1-12解：如图21所示，设水面为CF ，A 到水面C 的距离为L 1，B 灯与C 之间的距离为L 2，人眼到F 之间的距离为L 3，C 、D 之间的距离为L 4，由A 灯光的反射得3144L L L L L =-，代入数据得5.05.15.05.01544++=-L L ,得L 4=5m.对B 灯光的折射过程sini=sin ∠CBD=,55222L + sinr=sin ∠CA′D=,5522l +,3.111sin sin ==n r i 代入数据得：L 2=4.35 m,即灯光在水面下4.35 m 深处.图21答案：4.35 m。

第十三章 第一节 光的反射和折射基础夯实一、选择题(1～4题为单选题，5、6题为多选题)1．如图所示，国家游泳中心“水立方”的透明薄膜“外衣”上点缀了无数白色亮点，他们被称为镀点，北京奥运会举行时正值盛夏，镀点能改变光线方向，将光线挡在场馆外，镀点对外界阳光的主要作用是( A )A ．反射太阳光线，遵循光的反射定律B ．反射太阳光线，不遵循光的反射定律C ．折射太阳光线，遵循光的折射定律D ．折射太阳光线，不遵循光的折射定律解析：“挡在场馆外”一定是反射，只要是反射就一定遵循光的反射定律。

2．(鹤岗一中2015～2016年高二下学期期中)一束光线从空气射向折射率为1.5的玻璃内，入射角为45°，下面光路图中正确的是( C )解析：光在两介质的界面上通常同时发生反射和折射，所以A 错误；由反射定律和反射角为45°，根据折射定律n ＝sin θ1sin θ2得θ1>θ2，故B 错误；C 正确，D 错误。

3．检查视力时人与视力表之间的距离应为5m ，现因屋子太小而使用一个平面镜，视力表到镜子的距离为3m ，如图所示，那么人到镜中的视力表的距离和人到镜子的距离分别为( A )A ．5m,2mB ．6m,2mC ．4.5m,1.5mD ．4m,1m解析：根据平面镜成像规律可知选项A 正确。

4．(天津市静海一中2017年高二下学期检测)如图所示为光由玻璃射入空气中的光路图，直线AB 与CD 垂直，其中一条是法线。

入射光线与CD 的夹角为α，折射光线与CD 的夹角为β，α>β(α＋β≠90°)，则该玻璃的折射率n 等于( B )A ．sin αsin βB ．cos βcos αC ．cos αcos βD ．sin βsin α解析：因为光从玻璃射入空气，折射角大于入射角，所以知CD 为界面，入射角为90°－α，折射角为90°－β，根据光的可逆性知，折射率n ＝－β－α＝cos βcos α。