下载文档原格式
悬臂梁受力分析报告高一博2016.11.13西安理工大学机械与精密仪器工程学院摘要利用ANSYS对悬臂梁进行有限元静力学分析,得到悬臂梁的最大应力和挠度位移。
从而校验结构强度和尺寸定义，从而对结构进行最优化设计修正。
关键词：悬臂梁，变形分析，应力分析目录一.问题描述： (4)二.分析的目的和内容： (4)三.分析方案和有限元建模方法： (4)四.几何模型 (4)五．有限元模型 (4)六．计算结果： (5)七.结果合理性的讨论、分析 (8)八．结论 (8)参考文献 (8)一.问题描述：现有一悬臂梁，长500MM，一端固定，另外一端施加一个竖直向下的集中力200N。
其截面20MMX20MM的矩形，现在要分析该梁的在集中力作用下产生的位移，应力和局部应力。
二.分析的目的和内容：1.观察悬臂梁的变形情况；2.观察分析悬臂梁的应力变化；3.找出其最大变形和最大应力点，分析形成原因；三.分析方案和有限元建模方法：1.使用ANSYS-modeling-create-volumes-block建模，2.对梁进行材料定义，网格划分。
3.一端固定，另外一端施加一个向下的200N的力。
4.后处理中查看梁的应力和变形情况。
四.几何模型500X20X20的梁在在ANSYS中进行绘制.由于结构简单规则，无需简化。
五．有限元模型单元类型：solid brick8node45材料参数：弹性模量2e+11pa,泊松比0.3边界条件：一端固定，一端施加载荷载荷：F=200N划分网格后的悬臂梁模型六．计算结果：变形位移图等效应力图局部应力图七.结果合理性的讨论、分析1.位移分析：在变形位移图上，在约束端位移最小为零，受压端位移最大。
与实际结果一致。
2.应力分析：在应力图上，应力最大处在约束端，而最小的位于受压端，与变形图相对应。
通过材料力学计算可知约束端的所受弯矩最大。
两个结果印证无误。
3.局部应力分析：在局部应力图上，可以看出在固定端上表面存有较大的应力，且为拉应力，受压端直角尖处有最大应力，从形成原因上分析属于尖角处应力集中。
ANSYS APDL命令流悬臂梁分析教程本文通过分析悬臂梁介绍了ANSYS APDL相关命令流方法。
考虑悬臂梁如图2-2，求x=L变形量。
已知条件：杨氏系数E=200E9;截面参数：t=0.01m, w=0.03m, A=3E-4,I=2.5E-9;几何参数：L=4m, a=2m, b=2m;边界外力F=2N,q=0.05N/m.使用ANSYS解决该问题的命令如下：/FILNAM,EX2-1? ! 定义文件名/TITLE,CANTILEVER BEAM DEFLECTION? !定义分析的标题/UNITS,SI !定义单位制(注意观察输出窗口的单位)/PREP7 !进入前置处理ET,1,3? !定义元素类型为beam3MP,EX,1,200E9 ! 定义杨氏模量R,1,3E-4,2.5E-9,0.01 !定义实常数(要严格根据该元素类型的说明文档所给出的实常数格式)N,1,0,0!定义第1号节点X坐标为0，Y坐标为0N,2,1,0!定义第2号节点X坐标为1，Y坐标为0N,3,2,0 !定义第3号节点X坐标为2，Y坐标为0N,4,3,0 !定义第4号节点X坐标为3，Y坐标为0N,5,4,0!定义第5号节点X坐标为4，Y坐标为0E,1,2!把1、2号节点相连构成单元，系统将自定义为1号单元E,2,3!把2、3号节点相连构成单元，系统将自定义为2号单元E,3,4!把3、4号节点相连构成单元，系统将自定义为3号单元E,4,5!把4、5号节点相连构成单元，系统将自定义为4号单元FINISH? !退出该处理层/SOLU!进入求解处理器D,1,ALL,0 !对1节点施加约束使它X，Y向位移都为0F,3,FY,-2 !在3节点加集中外力向下2NSFBEAM,3,1,PRES,0.05 !在3 号元素的第1个面上施加压力(beam3有四个面可通过命令help,beam3查看，任何一个命令都可以通过help,命令查看帮助文档)SFBEAM,4,1,PRES,0.05 !同上在4号元素的第1个面加压力SOLVE !计算求解FINISH !完成该处理层/POST1!进入后处理SET,1,1!查看子步1，在有限元中复杂的载荷可以看做简单的载荷相互叠加，在ANSYS中每施加一类载荷都可以进行一次求解，可以查看它对结构的影响，称为子步。
第6例 杆系结构的静力学分析实例—悬臂梁[本例提示] 介绍了利用ANSYS 对杆系结构进行静力学分析的方法、步骤和过程。
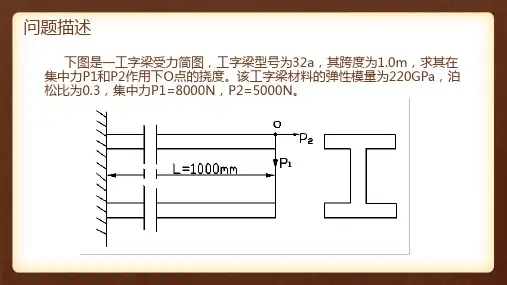
6.1 问题描述及解析解图6-1所示为一工字悬臂梁，分析其在集中力P 作用下自由端的变形。
已知梁的材料为10号热轧工字钢，其横截面面积A =14.345 cm 2，截面高度H =100 mm ，惯性矩I xx =245 cm 4。
梁的长度L =1 m ，集中力P =10000 N 。
钢的弹性模量E =2×1011 N/m 2，泊松比μ=0.3。
根据材料力学的知识，该梁自由端的挠度为 38113xx 310803.61024510231100003--⨯=⨯⨯⨯⨯⨯==EI PL f m （6-1） 6.2 分析步骤6.2.1 过滤界面拾取菜单Main Menu →Preferences 。
弹出的图6-2所示的对话框，选中“Structural ”项，单击“Ok ” 按钮。
图 6-1 悬臂梁图 6-2 过滤界面对话框52 ANSYS 在机械工程中的应用25例图 6-3 单元类型对话框 6.2.2 创建单元类型拾取菜单Main Menu →Preprocessor →Element Type →Add/Edit/Delete 。
弹出的图6-3所示的对话框，单击“Add ”按钮；弹出的图6-4所示的对话框，在左侧列表中选“Structural Beam ”，在右侧列表中选“2D elastic 3”， 单击“Ok ” 按钮；返回到图6-3所示的对话框，单击图6-3所示的对话框的“Close ”按钮。
6.2.3 定义实常数拾取菜单Main Menu →Preprocessor →Real Constants →Add/Edit/Delete 。
在弹出的“Real Constants ”对话框中单击“Add ”按钮，再单击随后弹出的对话框的“Ok ” 按钮，弹出图6-5所示的对话框，在“AREA ”、“IZZ ”、“HEIGHT ”文本框中分别输入、245e-8、0.1，单击“Ok ” 按钮。
基于ANSYS 10.0对悬臂梁的强度及变形分析姓名：刘吉龙班级：机制0803班学号：200802070516对悬臂梁的受力及变形分析摘要：本研究分析在ANSYS10.0平台上，采用有限元法对悬臂梁进行强度与变形分析、验证此悬臂梁设计的合理性。
一、问题描述长度L=254 mm的方形截面的铝合金锥形杆，上端固定，下端作用有均布拉力P=68.9 Mpa，上截面的尺寸50.8×50.8 mm，下截面尺寸25.4×25.4 mm（见右图），弹性模量E=7.071×104 Mpa，泊松比μ=0.3，试用确定下端最大轴向位移δ和最大轴向应力。
试将分析结果与理论解进行比较，说明有限元分析的误差。
（理论解：最大轴向位移δ=0.1238 mm）。
二、建立有限元模型：定义模型单元类型为：solid（实体）95号单元，材料常数为：弹性模量E=7.071×104 Mpa，泊松比μ=0.3。
三、有限元模型图：建立有限元模型时，观察模型的形状可知，我们可以先建立模型的上下底面，再根据有上下底面形成的八个关键点（keypoints）生成线，接着生成面，生成体。
最后生成该悬臂梁的模型图，示图如下：整个模型建立好之后即可对其划分网格，划分网格时，若选择自由划分则生成的网格比较混乱，不能比较准确的模拟该梁真实的受力变形情况。
故我们选择智能划分模式，并且分别对模型的各个棱边（lines）进行均匀分割，这样可以划分出比较理想的网格，更利于我们的研究和分析。
网格划分之后的模型图为：四、加载并求解：根据该悬臂梁的受力特点，我们在其下底面（比较大的底面）上进行六个自由度的位移约束，而在其上地面上施加大小为P=68.9 Mpa均布拉力，将载荷加载好之后便可进行运算求解，求解完成之后，我们得到其位移变形图如下：Z向位移云图为：Z向应力云图为：五、结果分析及结论：由以上两张云图和一张变形图中我们可以读出，悬臂梁的最大轴向（Z向）位移和轴向（Z向）最大应力分别为：最大轴向位移为：δ=0.123746 mm 最大轴向应力为：σ=68.224 Mpa 但是，我们知道，如果所划分的网格有差异时，计算结果将会产生一定的误差，由于设计要求的最大轴向位移不能超过0.1238mm，而我们的建模计算结果已经小于此设计要求值。
Ansys Workbench是一款广泛应用于工程领域的有限元分析软件，可以用于解决各种结构力学、流体动力学、电磁场等问题。
本文将以Ansys Workbench为例，介绍一个结构力学的例题，并详细讲解解题过程。
1. 问题描述假设有一个悬臂梁，在梁的自由端施加一个集中力，要求计算梁的应力分布和挠度。
2. 建模打开Ansys Workbench软件，新建一个静力学分析项目。
在几何模型中，画出悬臂梁的截面，并确定梁的长度、宽度和厚度。
在材料属性中，选择梁的材料，并输入对应的弹性模量和泊松比。
在约束条件中，将梁的支座固定，模拟悬臂梁的真实工况。
在外部荷载中，施加一个与梁垂直的集中力，确定力的大小和作用位置。
3. 网格划分在建模结束后，需要对悬臂梁进行网格划分。
在Ansys Workbench 中，可以选择合适的网格划分方式和密度，以保证计算结果的准确性和计算效率。
通常情况下，悬臂梁的截面可以采用正交结构网格划分，梁的长度方向可以采用梁单元网格划分。
4. 设置分析类型在网格划分完成后，需要设置分析类型为结构静力学。
在分析类型中，可以选择加载和约束条件，在求解器中，可以选择计算所需的结果类型，如应力、应变、位移等。
5. 求解和结果分析完成以上步骤后，可以提交计算任务进行求解。
Ansys Workbench软件会自动进行计算，并在计算完成后给出计算结果。
在结果分析中，可以查看悬臂梁的应力分布图和挠度图，进一步分析梁的受力情况和变形情况。
6. 参数化分析除了单一工况下的分析，Ansys Workbench还可以进行参数化分析。
用户可以改变材料属性、外部加载、几何尺寸等参数，快速地进行批量计算和结果对比分析，以得到最优的设计方案。
7. 结论通过Ansys Workbench对悬臂梁的结构分析，可以得到悬臂梁在外部加载下的应力分布和挠度情况，为工程设计和优化提供重要参考。
Ansys Workbench还具有丰富的后处理功能，可以绘制出直观的分析结果图，帮助工程师和研究人员更好地理解和使用分析结果。
工程地质数值模拟成绩考核——昆明理工大学本科生课程*****学院：国土资源工程学院科系：地科系专业：勘查111学号：************2014年11 月8 日悬臂梁的有限元分析1.问题概述。
悬臂梁为矩形截面的钢梁，长10m宽1m、高2m，不计梁的自重，弹性模量为220GPa，泊松比为0.2，在悬臂端作用一集中荷载P=1200kN。
试分析该悬臂梁的内力和变形情况。
2.启动ANSYS程序。
(1)在【开始】菜单中依次选取【所有程序】/【ANSYS8.0】/【ConfigureANSYSProducts】选项，打开【ANSYS8.0Launcher】对话框。
(2)选中【FileManagement】选项卡，输入目录名：“D:\ANSYSFX\zhang1\Exam01\ANSYSjs”，输入项目名：“Z101Beam”。
(3)单击按钮运行程序，进入ANSYS使用界面。
3.定义材料、实常数和单元类型。
(1)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】（前处理）/【ElementType】/【Add/Edit/Delete】选项，打开单元类型对话框。
单击按钮，打开单元类型库对话框，在右侧两个列表框中分别选取【Beam】选项和【2Delastic3】选项（简称为Beam3单元，以后叙述中记为【Beam】-【2Delastic3】单元，类似的情况记法相同），如图1-16所示。
单击按钮，再单击【ElementType】对话框中的按钮。
图1-16【LibraryofElementTypes】对话框(2)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】/【RealConstants】/【Add/Edit/Delete】选项，打开实常数对话框，如图1-17所示。
单击按钮，打开Beam3实常数对话框，按照提示输入相应的面积、惯性矩和梁高参数，如图1-18所示。
自定义截面梁的ANSYS求解ANSYS有多种梁截面的形状可供选择，但是如果ANSYS里面没有你想要的梁截面该怎么办呢？那就需要自己定义自己喜欢的梁截面。
下面给出命令流，可以很好地定义自己喜欢的梁截面。
先把效果展示给大家，命令流只是用来学习的，放在文章的最后。
我要分析的一个问题是一根L=1m长的矩形截面梁，一端固定一端自由（悬臂梁）。
矩形截面的B×H=0.1m×0.1m，梁上表面受均布荷载q=1000N/m，梁的弹性模量为E= 210GPa。
这个是可以通过理论计算得到梁末端最大挠度：w=qL48EI=1000×148×210×109×112×0.1×0.13=57×10−4≈0.714×10−4（m）截面的定义可以直接在ANSYS中进行，先定义好面，然后用MESH200单元进行网格划分，最后保存为*.rect文件，然后在进行梁单元建模的时候，导入截面参数文件，最后赋予梁该截面形状，进行梁单元网格剖分，施加荷载和边界条件，进行求解。
如下图所示，即定义好的梁截面形状。
可以看到界面的各个系数。
然后建模求解。
静力学求解一个Solve命令就行了。
最后可以画出变形图和应力云图。
应力云图如下。
由变形图可以得到该悬臂梁模型用ANSYS计算出来的最大末端位移是0.724×10−4（m），应力云图可以获知最大拉应力和最大压应力的大小相等为2.72MPa，求解成功。
万冀2017.01.03 于珞珈山（附：ANSYS命令流于后两页）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40finish/clear/prep7!利用MESH200单元对自定义梁截面进行网格剖分et,1,mesh200!*设置KeyOpt(1)=7即八节点四边形单元（截面划分网格必须这样）keyopt,1,1,7!*定义关键点k,1,0.0,0.0k,2,0.1,0.0k,3,0.1,0.1k,4,0.0,0.1!*连接关键点l,1,2l,2,3l,3,4l,4,1!*由线条构成截面al,1,2,3,4!*映射网格划分mshape,0,2dmshkey,1esize,0.01 !控制网格大小asel,,,,1amesh,all !划分网格!将自定义截面参数输出到文件mysec.sect文件中保存secwrite,mysec,sect,,1finish!**清空以往数据并开始新的计算/clear/prep7et,1,beam188mp,dens,1,7850mp,ex,1,2.1e11mp,prxy,1,0.3!***导入自定义截面sectype,1,beam,meshsecoffset,cent41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73secread,'mysec','sect',,meshsecplot,1,1 !**画出截面形状和网格r,1,k,1,0,0k,2,1,0k,3,0,1 ! 给梁单元定方向的3号关键点l,1,2,10 ! 连接关键点1和2并预划分10份!**LATT,-材料-实常数-单元类型-空-方向关键点号-空-梁截面编号latt,1,1,1,,3,,1esize,0.1 ! 划分单元大小lmesh,1sfbeam,all,1,pres,1000,,,,,,0 ! 施加均布压力(量纲：F/L) nsel,s,loc,x,0 ! 选取x=0处的节点施加固定约束(即模拟悬臂梁) d,all,allfinish!****静力求解/soluantype,0allsel,allsolvefinish/post1!*画变形图pldisp,1!*显示单元形状/eshape,1.0!*画x方向的应力云图plnsol,s,x/view,1,1,1,1/replot。
钢筋混凝土悬臂梁ANSYS优化设计与传统优化设计的对比分析摘要：提出了钢筋混凝土悬臂梁的力学模型，对钢筋混凝土悬臂梁的优化进了探讨，并对比了钢筋混凝土悬臂梁的ansys优化设计和钢筋混凝土悬臂梁的传统优化设计。
关键词：钢筋混凝土，优化设计，悬臂梁，ansys1钢筋混凝土悬臂梁的力学模型目前在钢筋混凝土建筑中，常见悬臂梁的长度多为两米以内。
为尽可能与实际相符，在此选用两种常见的跨度 1.5m 及 2m 对悬臂梁进行分析对比。
梁的截面宽度分别选b=150、200、250、300mm 四种常用的情况，并根据矩形截面梁高宽比的一般取值（常为h/b=2.0~3.5）确定对应的截面高度 h。
梁除自重 g 外沿全跨承受均布载荷设计值 q。
截面的配筋方式采用单筋矩形截面的配筋方式。
钢筋混凝土悬臂梁设计计算时的力学模型见图 1：图 1 钢筋混凝土悬臂梁设计计算力学模型假设两种钢筋混凝土悬臂梁的基本信息如下：矩形钢筋混土悬臂梁，长度为 l=1.5m，截面宽度为 b，高度为度 h，保护层厚度为as，全跨受均布荷载作用 q=50 kn/m，混凝土等级为 c30, fc=14.3 n/mm2, ft= 1.43n/mm2弹性模量ec=3.0104n/mm2，纵向受力筋采用 hrb335, fy= fy′= 300n/mm2，es=2.0105n/mm2，构造筋采用 hpb235, fy = fy′= 210n/mm2，es=2.1105n/mm2，环境类别为二类 b。
悬臂梁长度为 l=2m 时取相同等级的材料进行设计计算。
2钢筋混凝土悬臂梁的优化思路在结构初步设计的基础上，可以进行优化设计。
优化设计是一种寻找确定最优设计方案的技术，所谓“最优设计”，指的是一种方案可以满足所有的设计要求，而且所需的支出，如重量、面积、体积、应力、费用等最小，也就是说，最优设计方案就是一个最有效率的方案。
对于钢筋混凝土梁单筋矩形截面，当梁上作用的荷载一定时，梁的截面尺寸和配筋有多种方案。
