高新一中八年级数学上册自学导案

课题：一次函数复习专题【类型一】利用一次函数的定义 (m 22)x m 3 (m 4)是一次函数？例1、当m 为何值时，函数yH练习：①当m= 时，y (m3)x 2m 1 4x 5是一次函数。

②已知函数 y (k 2)x xk 1,当=时，它是一次函数；当=时，它是正比例函数..2③已知函数y=(k-1)x k + m-2, (1)若它是一个正比例函数，求k , m 的植.(20若它是一个一 次函数，求k , m 的植.来源学科网］例2.已知y 是关于x 的一次函数，且当 x = 3时，y=-2，当x = -2时，y=5，求这个一次函 数的解析式•例3.已知y+b 与x+a(其中a 、b 是常数)成正比.(1) 试说明：y 是x 的一次函数；⑵ 若x=3时，y=5; x=2时，y=2,求函数的表达式.练习：①已知y 是关于x 的一次函数，且当x = -2时，y=-3，当x = 1时，y=3,求这个一次函数的 解析式•并求x=-5时的函数值.②若y 与(x-3)成正比例，且x=4时，y=-1，则y 与x 的函数关系式是什么?1例4.已知一次函数y=—x —5.①求该函数图象与坐标的交点坐标，并画出其图象.②求函2数图象与两坐标轴围成的三角形的面积.练习。

(1)已知两条直线y=^x—5和y= —2 x+4,求它们与坐标轴共同围成的图形的面积. 2(2 )一次函数y kx b的图像在y轴上的截距为4,与x轴、y轴分别交于P、Q两点,且厶OPQ的面积为8,求一次函数从解析式。

(3)已知函数y1 k1x b的图像过点(一1,-5 )和(2,4 ),函数y2 k2x b2的图像于直线y = 2x平行，且过点(1,1 )。

(1)求出这两个函数的解析式；(2)若「这两个函数值同时为正，求x的取值范围；(3)求这两个函数与y 轴所围成三角形的面积。

1(4)如果把直线y -x m向上平移1个单位后，所得的直线与两条坐标轴所围成的面积为4，求m的值。

课题：__________________________________________一、回顾复习，温故引新，明确目标。

1. _____________________________________________________________ 你重点学习了。

2.上节课的老牛和小马的包裹谁的多的问题，经过大家的共同努力，得出了二元一次方程组一x-y=2一x+ 仁2(y-1)①到底谁的包裹多呢？②这就需要解这个二元一次方程组3.本节重点研究的问题：（1.）会用代入消元法解二元一次方程组（2）.了解解二元一次方程组的消元思想，初步体现数学研究中化未知为已知”的化归思想，从而“变陌生为熟悉” 二、精研课本，参考教辅，探索新知（一）实践探索，感悟新知。

1. 自学课本P221的引例，注意以下说明。

我们大家知道二元一次方程只需要消去一个未知数就可变为一元一次方程，那么我们发现：由①得y=x-2由于方程组相同的字母表示同一个未知数，所以方程②中的y也等于x-2,可以用x-2代替方程②中的y.这样就得到大家会解的一元一次方程了.2. 完成课本P221例1、例2,并与课本比较。

解：解:r[ 来源:]（二）归纳提炼，形成概念。

1•上面解方程组的基本思路是什么？主要步骤有哪些？（1）基本思路是： ______________________________________________________________________ 。

_ （2）主要步骤是：①将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来，②将这个代数式代入另一个方程中，从而消去一个未知数，化二元一次方程组为一元一次方程式。

③解这个一元一次方程。

④把求得的一次方程的解代入方程中，求得另一个未知数值，组成方程组的解。

这种解方程组的方法称为代入消元法。

简称代入法。

解题步骤概括为三步即：①变、②代、③解、2. 请同学们把一次函数的定义多读几遍，再通过研读教辅，你对新概念又有了哪些更深的认识？三、学以致用，理解新知，巩固新知。

课题：一．基础回顾： 1.算术平均数：2.加权平均数：3.（1）如果一组数据5，x ，3，4的平均数是5，那么x=_______．（2）某校八年级（一）班一次数学考试的成绩为：100分的3分，90分的13人，80•分的17人，70分的12人，60分的2人，50分的3人，全班数学考试的平均成绩是_______． （结果保留到个位）二．明确目标：1.会求加权平均数，并体会权的差异对结果的影响.2.理解算术平均数和加权平均数的联系和区别，并能利用它们解决一些现实问题. 发展学生的求同和求异思维. 三．探索新知： （一）自主探究1.阅读并完成P255。

2.思考并完成课本P255“议一议”小明的做法是31(9%+30%+6%)=15%因为小颖家去年的饮食、教育和其他三项支出金额不等，因此饮食、教育和其他三项支出的增长率“地位”不同，它们对总支出增长率的“影响”不同.不能简单地用算术平均数计算总支出的增长率，而应将这三项支出金额3600、1200、7200分别视为三项支出增长率的“权”，从而求总支出的增长率。

（二）感悟与收获日常生活中的诸多“平均”现象并非算术平均.由于多数情况下，各项的重要性不一定相同(即权数不同)，应将其视为加权平均.如彩票的平均收益，不是各个等次奖金金额的算术平均数，而应考虑不同等次奖金的获奖比例.（三）完成课本P256随堂练习和议一议四．拓展与探究：1．老王家的鱼塘中放养了某种鱼1500条，若干年后，准备打捞出售，为了估计鱼塘中这种鱼的总质量，现从鱼塘中捕捞三次，得到数据如下表：（1）鱼塘中这种鱼平均每条重约多少千克？（2）若这种鱼放养的成活率是82%，鱼塘中这种鱼约有多少千克？（3）如果把这种鱼全部卖掉，价格为每千克6.2元，那么这种鱼的总收入是多少元？若投资成本为14000元，这种鱼的纯收入是多少元？2.某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变，有关数据如下表所示：（1）该风景区称调整后这5个景点门票的平均收费不变，平均日总收入持平，问风景区是怎样计算的？（2）另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，•实际上增加了约9.4%，问游客是怎样计算的？ （3）你认为风景区和游客哪一个说法较能反映整体实际？五．检测反馈：1.如果一组数据x 1，x 2，x 3，x 4的平均数是x ，那么另一组数据x 1，x 2+1，x 3+2，x 4+3的平均数是（ ）A ．xB ．x +1C ．x +1.5D ．x +62.有m 个数的平均数是x ，n 个数的平均数是y ，则这（m+n ）个数的平均数为（ ）A...22x y x y mx ny mx nyB C D m nm n++++++3.x 1，x 2，x 3，……，x 10的平均数是5，x 11，x 12，x 13，……，x 20的平均数是3，则x 1，x 2，x 3，……，x 20的平均数是（ ）A ．5B ．4C ．3D ．84.某居民院内月底统计用电情况，其中3户用电45度，5户用电50度，6户用电42度，则平均每户用电（ ）A ．41度B ．42度C ．45.5度D ．46度5.甲、乙、丙三种糖果售价分别为每千克6元，7元，8元，若将甲种8千克，•乙种10千克，丙种3千克混在一起，则售价应定为每千克（ ） A ．6.7元 B ．6.8元 C ．7.5元 D ．8.6元6.为了增强市民的环保意识，某初中八年级（二）班的50名学生在今年6月5日（•世界环请根据以上数据回答：（1）50户居民每天丢弃废旧塑料袋的平均个数是______个．（2）该校所在的居民区有1万户，则该居民区每天丢弃的废旧塑料袋约_____万个．7.某商场四月份随机抽查了6天的营业额，结果分别如下（单位：万元）：2.8，•3.2，3.4，3.0，3.1，3.7，试估算该商场四月份的总营业额，大约是______万元．8.某班进行个人投篮比赛，受污染的下表记录了在规定时间内投进n•个球的人数分布情况，同时，已知进球3个或3个以上的人平均每人投进3．5个球；进球4个或4个以下的人平均每人投进2．5个球，问投进3个球和4个球的各有多少人？六、学后反思。

课题： ____________________________ z____________一、回顾复习，温故引新，明确目标。

1. 一次函数的图象及性质： _____________________________________________________________ ［来源:］2. 一次函数y = kx + b （k丰0）的图像是 _______ ，要画一次函数的图像，只需取直线上的（在选点时要能使计算尽可能简便）；特殊的一次函数一一正比例函数y= kx （k工0）的图像是一条经过_____ 的直线，要画它的图像只需再取点_________ .3. 在一次函数y= kx + b （k丰0）中，当k的值相同时，几条直线__________ ;若几条直线互相平行，则他们函数关系中的___________ 此时可以把其中的某条直线看成是由另一条直线上下平移而得到的来源学。

科。

网］4. 在一次函数y= kx + b （k z 0）中，b的值确定直线与y轴的交点的位置，即图像与y轴的交点坐标为（0, b），当b>0时，交点在x轴上方；当b<0时，交点在x轴下方；当b = 0 时，图像经过原点5. 满足关系Y=kX+b的x, y所对应的点（x, y）都在一次函数Y=kX+b的图象上；在一次函数Y=kX+b的图象上的点（x, y）都满足关系Y=kX+b=6粗读一遍这节课重点研究什么？二、精研课本，参考教辅，探索新知。

1. 完成课本P202引例2. 完成课本P203例23. 课本引例和例2给你什么启示？设计这两题的意图是什么？还有其他方法吗学以致用，理解新知，巩固新知。

[来源 :学I 科I 网 Z|X|X|K]1•一辆速度为90千米/小时汽车由赣州匀速驶往南昌，下列图像中能大致反映汽车行驶路程 s （千米）和行驶时间t （小时）的关系的是（）2•为了鼓励小强勤做家务，培养他的劳动意识，小强每月的费用都是根据上月他的家务劳动 时间所得奖励加上基本生活费从父母那里获取的•若设小强每月的家务劳动时间为x 小时,该月可得（即下月他可获得）的总费为y 元，贝U y （元）和x （小时）之间的函数图像如图所示.（1 ）根据图像，请你写出小强每月的基本生活费为多少元；父母是如何奖励小强家务劳动 的？ （2） 写出当O W x <2时，相对应的y 与x 之间的函数关系式；（3） 若小强5月份希望有250元费用，则小强4月份需做家务多少时间？ 思考提炼：通过函数图像获取信息需注意（ 1 ）横坐标所代表的 _____________ ;（）纵坐标所代表的 ________________ 。

高新一中八年级数学上册自学导案14课题：________________________________________一、回顾复习，温故引新，明确目标。

1.一次函数的图象及性质：___________________________________________________________ ___2.一次函数y=kx+b（k丰0）的图像是_________，要画一次函数的图像，只需取直线上的（在选点时要能使计算尽可能简便）；特殊的一次函数一一正比例函数y=kx（k工0）的图像是一条经过_____的直线，要画它的图像只需再取点_________.3.在一次函数y=kx+b （k丰0）中，当k的值相同时，几条直线___________;若几条直线互相平行，则他们函数关系中的____________此时可以把其中的某条直线看成是由另一条直线上下平移而得到的［来源学+网Z+X+X+4.在一次函数y=kx+b（kM0）中，b的值确定直线与y轴的交点的位置，即图像与y轴的交点坐标为（0,b）,当b0「时，交点在x轴上方；当b0时，交点在x轴下方；当b=0时，图像经过原点5.满足关系Y=kX+b 的x,y所对应的点（x,y）都在一次函数Y=kX+b的图象上；在一次函数Y=kX+b的图象上的点（x,y）都满足关系Y=kX+b=6粗读一遍这节课重点研究什么？、精研课本，参考教辅，探索新知。

1.观察图象并回答问题：当x=20时，y=________________时,x=________。

图中的函数关系式是_________________,值范围是__________。

当y=500它的自变量取2观察图象回答下列问题：当x_____时,y0；当x时,y0来源:ZxxkCom］［来源学*科*网］时,y=0；3完成课本P198引例4完成课本P199例15课本引例和例1给你什么启示?1.学以致用，理解新知，巩固新知。

课题：一、回顾复习，温故引新，明确目标。

1.一次函数的图象及性质：2.一次函数y ＝kx ＋b （k ≠0）的图像是 ，要画一次函数的图像，只需取直线上的 （在选点时要能使计算尽可能简便）；特殊的一次函数——正比例函数y ＝kx （k ≠0）的图像是一条经过 的直线，要画它的图像只需再取点 .3. 在一次函数y ＝kx ＋b （k ≠0）中，当k 的值相同时，几条直线 ;若几条直线互相平行，则他们函数关系中的 。

此时可以把其中的某条直线看成是由另一条直线上下平移而得到的4. 在一次函数y ＝kx ＋b （k ≠0）中，b 的值确定直线与y 轴的交点的位置，即图像与y 轴的交点坐标为（0，b ），当b>0时，交点在x 轴上方；当b<0时，交点在x 轴下方；当b ＝0时，图像经过原点5．满足关系Y=kX+b 的x ，y 所对应的点（x ，y ）都在一次函数Y=kX+b 的图象上；在一次函数Y=kX+b 的图象上的点（x ，y ）都满足关系Y=kX+b 。

6粗读一遍这节课重点研究什么？二、精研课本，参考教辅，探索新知。

1.完成课本P202引例2.完成课本P203例23.课本引例和例2给你什么启示？设计这两题的意图是什么？还有其他方法吗 ？三、学以致用，理解新知，巩固新知。

1.一辆速度为90千米/小时汽车由赣州匀速驶往南昌，下列图像中能大致反映汽车行驶路程s（千米）和行驶时间t（小时）的关系的是( )2.为了鼓励小强勤做家务，培养他的劳动意识，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的．若设小强每月的家务劳动时间为x小时，该月可得（即下月他可获得）的总费为y元，则y（元）和x（小时）之间的函数图像如图所示．（1）根据图像，请你写出小强每月的基本生活费为多少元；父母是如何奖励小强家务劳动的？（2）写出当0≤x≤20时，相对应的y与x之间的函数关系式；（3）若小强5月份希望有250元费用，则小强4月份需做家务多少时间？思考提炼：通过函数图像获取信息需注意（1）横坐标所代表的；（）纵坐标所代表的。

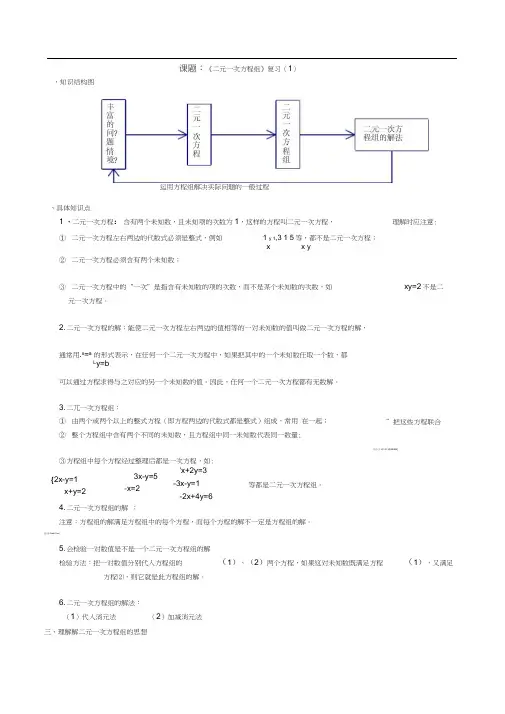
课题：《二元一次方程组》复习（1）、知识结构图、具体知识点1 •二元一次方程：含有两个未知数，且未知项的次数为1，这样的方程叫二元一次方程，理解时应注意:①二元一次方程左右两边的代数式必须是整式，例如 1 y 1,3 1 5等，都不是二元一次方程；x x y②二元一次方程必须含有两个未知数；③二元一次方程中的“一次”是指含有未知数的项的次数，而不是某个未知数的次数，如xy=2不是二元一次方程。

2. 二元一次方程的解：能使二元一次方程左右两边的值相等的一对未知数的值叫做二元一次方程的解，通常用.x=a的形式表示，在任何一个二元一次方程中，如果把其中的一个未知数任取一个数，都L y=b可以通过方程求得与之对应的另一个未知数的值。

因此，任何一个二元一次方程都有无数解。

3. 二兀一次方程组：①由两个或两个以上的整式方程（即方程两边的代数式都是整式）组成，常用在一起；②整个方程组中含有两个不同的未知数，且方程组中同一未知数代表同一数量;③方程组中每个方程经过整理后都是一次方程，如:4. 二元一次方程组的解：注意：方程组的解满足方程组中的每个方程，而每个方程的解不一定是方程组的解。

[来源:]5. 会检验一对数值是不是一个二元一次方程组的解检验方法：把一对数值分别代入方程组的（1）、（2）两个方程，如果这对未知数既满足方程（1），又满足方程⑵，则它就是此方程组的解。

6. 二元一次方程组的解法：（1）代入消元法（2）加减消元法三、理解解二元一次方程组的思想”把这些方程联合[来源:学#科#网Z#X#X#K]{2x-y=1x+y=23x-y=5-x=2'x+2y=3-3x-y=1-2x+4y=6等都是二元一次方程组。

运用方程组解决实际问题的一般过程四、解二元一次方程组的一般步骤(一)、代入消元法(1) 从方程中选一个系数比较简单的方程，将这个方程中的未知数用另一个未知数的代数式来表示, 如用T表示T，可写成⑴一①■'(2) 将“代入另一个方程，消去V，得到一个关于工的一元一次方程(3) 解这个一元一次方程，求出T的值；［来"学科网(4) 把求得的工'的值代入J 中，求出匸的值，从而得到方程组的解.(二)、加减法(1) 方程组的两个方程中，如果同一个未知数的系数既不互为相反数，也不相等时，可用适当的数乘以方程的两边，使一个未知数的系数互为相反数或相等，得到一个新的二元一次方程组；(2) 把这个方程组的两边分别相加(或相减) ，消去一个未知数，得到一个一元一次方程；(3) 解这个一元一次方程；(4) 将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解。

课题：一．基础回顾：一快车和一慢车沿相同路线从A 地到B 地，所行的路程与时间的函数图像如图所示，根据图像回答下列问题：（1）慢车比快车早出发 小时，快车追上慢车时行驶了 米,快车比慢车早 小时到达B 地（2）交点（4，276）所代表的实际意义是二．明确目标：1、能利用二元一次方程组确定一次函数关系表达式2、经历利用二元一次方程与一次函数关系解决实际问题的过程，进一步发展学数学用数学的意识。

三．探索新知：（一）自主探究1.阅读P241，先想一想你如何做。

再比较你的 做法与小明、小颖、小彬的做法有什么不同？ 通过解决以上问题你发现什么：（二）完成课本P242例2 解：例3.科学家通过实验得出一定质量的某气体在体积不变的情况下，压强p （千帕）随温度（℃）变化的函数关系式是p=kt+b ，其图像是如图所示的射线AB. （1）根据图像求出上述气体的压强p 与温度t 的函数关系式。

（2）求出当压强p 为200千帕时，上述气体的温度。

（三）P240随堂练习四．拓展与探究： 1.通过市场调查，一段时间内某地区某一种农副产品的需求数量y （千克）与市场价格x （元/千克）（030x <<）存在下列关系：x （元/千克）5 10 15 20 y （千克） 4500 4000 3500 3000又假设该地区这种农副产品在这段时间内的生产数量z （千克）与市场价格x （元/千克）成正比例关系：400z x =（030x <<）．现不计其它因素影响，如果需求数量y 等于生产数量z ，那么此时市场处于平衡状态．（1）请通过描点画图探究y 与x 之间的函数关系，并求出函数关系式；（2）根据以上市场调查，请你分析：当市场处于平衡状态时，该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少？2.第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y （千米）与时间x （小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港． （1）哪个队先到达终点？乙队何时追上甲队？（2）在比赛过程中，甲、乙两队何时相距最远？元／千克) （第8题图）时间/时164020五．检测反馈：1如图1，一次函数图象经过点A ，且与正比例函数y x =-的 图象交于点B ，则该一次函数的表达式为（ ）BA ．2y x =-+B ．2y x =+C ．2y x =-D ．2y x =--2.将直线y ＝2x 向右平移2个单位所得的直线的解析式是（ ）。

课题：一次函数复习专题【类型一】利用一次函数的定义例1、当m 为何值时，函数)4m (x )2m (y 3m 2-+--=-是一次函数？练习：①当m ＝______时，5x 4x )3m (y 1m 2-++=+是一次函数。

②已知函数1k x x )2k (y -+++=，当=_____时，它是一次函数；当＝______时，它是正比例函数. ③已知函数y=(k-1)x2k + m-2，（1）若它是一个正比例函数,求k , m 的植.（20若它是一个一次函数，求 k , m 的植．【类型二】待定系数法确定一次函数的解析式例2.已知y 是关于x 的一次函数，且当x ＝3时，y=-2，当x ＝-2时，y=5，求这个一次函数的解析式.例3.已知y+b 与x+a(其中a 、b 是常数)成正比． (1)试说明：y 是x 的一次函数；(2)若x=3时，y=5；x=2时，y=2，求函数的表达式．练习：①已知y 是关于x 的一次函数，且当x ＝-2时，y=-3，当x ＝1时，y=3，求这个一次函数的解析式.并求x=-5时的函数值.②若y 与(x-3)成正比例，且x=4时，y=-1，则y 与x 的函数关系式是什么？例4.已知一次函数y=21x －５．①求该函数图象与坐标的交点坐标，并画出其图象．②求函数图象与两坐标轴围成的三角形的面积．练习。

（1）已知两条直线y=21x －５和y=－２x+4，求它们与坐标轴共同围成的图形的面积．（2）一次函数b kx y +=的图像在y 轴上的截距为4，与x 轴、y 轴分别交于P 、Q 两点，且△OPQ 的面积为8，求一次函数从解析式。

（3）已知函数b x k y +=11的图像过点（－1,-5）和（2,4），函数222b x k y +=的图像于直线y ＝2x 平行，且过点（1,1）。

（1）求出这两个函数的解析式；（2）若这两个函数值同时为正，求x 的取值范围；（3）求这两个函数与y 轴所围成三角形的面积。

课题：「一、问题情境：我们伟大祖国具有五千年的文明史，在历史的长河中，为科学知识的创新和发展作出了 巨大的贡献，特别在数学领域有 ［九章算术］、［孙子算经］等古代名著流传于世，普及趋于民 众，许多问题浅显易懂，趣味性强，如［九章算术］下卷第三题目“雉兔同笼”等。

1•阅读课本P229—“雉兔同笼”（1）•用一元一次方程求解（2）.用二元一次方程求解：趣味题：一只蜘蛛有8只脚，一只蜻 蜓有6只脚。

如果蜘蛛和蜻蜓共有 76只脚，而且蜘蛛比蜻蜓多，那么， 蜘蛛和蜻蜓各有多少只？2. 本节重点研究的问题：1 •通过对实际背景的分析，领 会用二元一次方程组的知识与实际问题的紧密联系。

2•会从复杂的问题中提炼关键信息。

并能找出适当的等量关系。

从而正确地建立方程。

趣味题：我国古代算书《四元玉鉴》 有一名例，二果问价：九百九十九文钱，甜果苦果买一千， 甜果九个^一文，苦果七个四文钱， 试问甜果几个，又问各几个钱？（二）归纳提炼，1. 用二元一次方程组解应用题的 步骤是：“审、设、列、解、答”比较两种方法的优缺点:二、探索尝试 （一）实践探索。

1.完成课本P229的例。

解：三、学以致用：1•例2•某蔬菜公司收购到某种蔬菜 140吨，准备加工后上市销售，该公司的加工能力是：每天精加工6吨或者粗加工16吨，现计划用15天完成加工任务， 该公司安排几天粗加工， 几 天精加工，才能按期完成任务？如果每吨蔬菜粗加工后的利润为 1000元，精加工后为2000元那么该公司出售这些加工后的蔬菜共可获利多少元？分析：解决这个问题的关键是先解答前一个问题， 既先求出安排精加工和粗加工的天数， 如果我们用列方程组的办法来解答。

可设应安排 X 天精加工，Y 天粗加工，那么要找出能 反映整个题意的两个等量关系。

引导学生寻找等量关系。

（1） 精加工天数与粗加工天数的和等于15天。

（2） 精加工蔬菜的吨数与粗加工天蔬菜的吨数的和为 140吨。

课题： ________________________________________一•基础回顾：1把下列方程写成用含 x 的式子表示y 的形式：X(1 )若 2x — y=3 ,则 y= _____ ; (2)若 3x+y —仁0,则 y= ______ ; (3)若空 + y =6,则 y=2、已知二元一次方程 2x — 3y=1。

若x=3,则y= _________ ;若y=1,则y= _______ 。

二•明确目标：1、 会用加减消元法解二元一次方程组；2、 了解解二元一次方程组的消元思想，初步体会数学学习的化归思想 三.探究新知：(一)思考并做一做P224页小彬、小丽解方程组的方法 小彬的方法： , 小丽的方法：I I I I［卄网ZXXK ］ 'I *I I I II来源 学 &科&网 Z&X&X&K ］|观察与比较：他们两人解法有相同之处是： ______________不同之处是： ___________________________________。

(二) 试着用小丽的解法思想完成课本 P225例3、例4。

解：：解：I ! I I I I I I I I［来源:学科网］通过观察一一思考一一实践，然后自己去总结解题方法：当两个方程的同一个未知数的系数相同或互为相反数时， 可通过将方程组中的两个方程相减或相加，消去其中的一个未知数，转化为 一元一次方程，这种解二元一次方程组的方法叫做加减消兀法(简称加减法)。

评注：遇到新问题、较复杂的问题时，我 们通过观察、对比，概括 出它们形式上的 不同，再思考怎样用转化的思想对方程进 行适当的变形，想办法把它化归为已知的 问题、较简单的问题去解决，在学习中 体验转化思想的作用.（三）.完成课本P226随堂练习四•拓展与探究：点拨：因为绝对值、平方的结果都是非负数，而两个非负数的和等于零，只可能是两个数都为零.五•检测反馈:4x 3y 6,，若先求x的值，应先将两个方程组相4x 3y 2.求y的值，应先将两个方程组相 _____________4. 已知a+2b=3-m 且2a+b=-m+4,则a-b 的值为(A . 1B . -1C . 0D . m-12 35. 若2x5m+2n+2y3与-3x6y3m-2n-1的和是单项式，则m= _______ , n=3 42 •已知两数之和是36，两数之差是12,则这两数之积是（）A . 266B . 288C . -288D . -1242.已知:x 2y 3m 104x 3y 2m 15 ，求x y m的值。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

课题：一．基础回顾：1、把下列方程写成用含x的式子表示y的形式：（1）若2x－y=3 ,则y= ；(2) 若3x+y－1=0，则y= ；（3）若x2+y＝6,则y=2、已知二元一次方程2x－3y=1。

若x=3，则y= ；若y=1,则y= 。

二．明确目标：1、会用加减消元法解二元一次方程组；2、了解解二元一次方程组的消元思想,初步体会数学学习的化归思想三．探究新知：（一）思考并做一做P224页小彬、小丽解方程组的方法小彬的方法：小丽的方法：观察与比较：他们两人解法有相同之处是：不同之处是：。

（二）试着用小丽的解法思想完成课本P225例3、例4。

解：解:通过观察——思考——实践，然后自己去总结解题方法:当两个方程的同一个未知数的系数相同或互为相反数时，可通过将方程组中的两个方程相减或相加，消去其中的一个未知数，转化为一元一次方程，这种解二元一次方程组的方法叫做加减消元法（简称加减法）。

(三).完成课本P226随堂练习四．拓展与探究：1.已知|2x ＋3y ＋5|＋(3x ＋2y －25)2＝0，求x 、y2.已知：⎩⎨⎧=++=++152341032m y x m y x ，求m y x ++的值。

五．检测反馈：1．用加减法解方程组436,43 2.x y x y +=⎧⎨-=⎩，若先求x 的值，应先将两个方程组相_______；若先求y 的值，应先将两个方程组相________．2．已知两数之和是36，两数之差是12，则这两数之积是（ ）A ．266B ．288C ．-288D ．-1243．已知x 、y 互为相反数，且（x+y+4）（x-y ）=4，则x 、y 的值分别为（ ）A ．2,2x y =⎧⎨=-⎩B ．2,2x y =-⎧⎨=⎩C ．1,212x y ⎧=⎪⎪⎨⎪=-⎪⎩D ．1,212x y ⎧=-⎪⎪⎨⎪=⎪⎩4．已知a+2b=3-m 且2a+b=-m+4，则a-b 的值为（ ）A ．1B ．-1C ．0D ．m-15．若23x 5m+2n+2y 3与-34x 6y 3m-2n-1的和是单项式，则m=_______，n=________．6．用加减法解下列方程组：（1）3216,31;m n m n +=⎧⎨-=⎩ （2）234,443;x y x y +=⎧⎨-=⎩（3）523,611;x y x y -=⎧⎨+=⎩ （4）357,23423 2.35x y x y ++⎧+=⎪⎪⎨--⎪+=⎪⎩二、综合创新7．（综合题）已知关于x 、y 的方程组352,23x y m x y m +=+⎧⎨+=⎩的解满足x+y=-10，求代数m 2-2m+1的值．8．在解方程组2,78ax by cx y +=⎧⎨-=⎩时，哥哥正确地解得3,2.x y =⎧⎨=-⎩，弟弟因把c 写错而解得2,2.x y =-⎧⎨=⎩，求a+b+c 的值．答案：1．加；减 2．B 3．C 4．A ． 5．1；-1 26.（1）2,5.mn=⎧⎨=⎩（2）5,41.2xy⎧=⎪⎪⎨⎪=⎪⎩（3）5,413.8xy⎧=⎪⎪⎨⎪=⎪⎩（4）5,231.4xy⎧=⎪⎪⎨⎪=⎪⎩7．解：解关于x、y的方程组352,23x y mx y m+=+⎧⎨+=⎩得26,4.x my m=-⎧⎨=-+⎩把26,4.x my m=-⎧⎨=-+⎩代入x+y=-10得（2m-6）+（-m+4）=-10．解得m=-8．∴m2-2m+1=（-8）2-2×（-8）+1=81．8．解：把3,2.xy=⎧⎨=-⎩代入2,78ax bycx y+=⎧⎨-=⎩得322,3148.a bc-=⎧⎨+=⎩把2,2.xy=-⎧⎨=⎩代入ax+by=2 得-2a+2b=2．解方程组322,3148,22 2.a bca b-=⎧⎪+=⎨⎪-+=⎩得4,5,2.abc=⎧⎪=⎨⎪=-⎩∴a+b+c=4+5-2=7．六、学后反思。

☆ 高新一中八年级数学自学导案（14） 1 课题： 一、回顾复习，温故引新，明确目标。

1.一次函数的图象及性质：

2.一次函数y＝kx＋b（k≠0）的图像是 ，要画一次函数的图像，只需取直线上的 （在选点时要能使计算尽可能简便）；特殊的一次函数——正比例函数y＝kx（k≠0）的图像是一条经过 的直线，要画它的图像只需再取点 . 3. 在一次函数y＝kx＋b（k≠0）中，当k的值相同时，几条直线 ;若几条直线互相平行，则他们函数关系中的 。此时可以把其中的某条直线看成是由另一条直线上下平移而得到的 4. 在一次函数y＝kx＋b（k≠0）中，b的值确定直线与y轴的交点的位置，即图像与y轴的交点坐标为（0，b），当b>0时，交点在x轴上方；当b<0时，交点在x轴下方；当b＝0时，图像经过原点

5．满足关系Y=kX+b的x，y所对应的点（x，y）都在一次函数Y=kX+b的图象上；在一次函数Y=kX+b的图象上的点（x，y）都满足关系Y=kX+b。

6粗读一遍这节课重点研究什么？

二、精研课本，参考教辅，探索新知。 1.观察图象并回答问题：当x=20时，y=_______, 当y=500时,x=_________。图中的函数关系式是______________，它的自变量取值范围是_________。

2.观察图象回答下列问题：当x_____时,y＞0； 当x_______时,y=0； 当x________时,y＜0

3.完成课本P198引例 ☆ 高新一中八年级数学自学导案（14）

2 4.完成课本P199例1

5.课本引例和例1给你什么启示？ 1. 学以致用，理解新知，巩固新知。 1.完成课本P 200随堂练习。

2.在空中,自地面算起,每升高1千米,气温下降若干度（℃）.某地空中气温t (℃)与高度h（千米）间的函数的图象如图1所示,观察图象可知：该地地面气温为______℃,当高度h______

☆高新一中八年级数学自学导案（16）一次函数复习一、知识结构↓↓↙↘←→↓↓二、基础知识（一）函数中的常量与变量生活中到处着充满着变化的量，如：弹簧的长度与所挂物体的质量，路程的距离与所用时间……了解这些关系，可以帮助我们更好地认识世界。

下面我们就去复习有关变量与常量的问题。

1.一般地，在某个变化过程中，有两个变量x和y，如果给定一个x值，相应地就确定了一个y值，那么我们称y是x的函数，其中x是自变量，y是因变量。

2:函数的三种表示方法：（1）图象；（2）表格；（3）关系式。

3:求函数的值：在一个函数关系式中，能识别自变量与因变量，给定自变量的值，相应地会求出函数的值。

如:已知函数Y=(X2-9)/(X2-2X-3),当X=1时,函数值Y为多少?当X为何值时,函数值Y为0?（二）一次函数的概念、图像及性质1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。

当b_____时，函数y=____(k____)叫做正比例函数。

理解一次函数概念应注意下面两点：⑴解析式中自变量x的次数是___次，⑵比例系数_____。

2、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的______。

3、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。

4、正比例函数y=kx（k≠0)的性质：正比例函数是特殊的一次函数。

⑴当k>0时，图象过______象限；y随x的增大而____。

⑵当k<0时，图象过______象限；y随x的增大而____。

5、一次函数y=kx+b(k ≠ 0)的性质：平行于 y = k x ,可由它平移而得⑴当k>0时，y随x的增大而_________。

⑵当k<0时，y随x的增大而_________。

⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号：k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;k>0,b<0时在Ⅰ, Ⅲ, Ⅳ象限k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限. k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限6、求一次函数的表达式就是利用________个条件求k和b三、巩固网络填空题：(1) 有下列函数：①y=2x, ②y=-2x+1，③y=x+5, ④ y=2x-3 。

课题：一．基础回顾：1．什么是二元一次方程？什么是二元一次方程的解？二元一次方程的解的个数如何？2.一次函数是： ，它的图像是 。

3.如果将二元一次方程x +y =8利用等式的性质变形，就可得到y =8－x ，同学们能联想到什么？二．明确目标：1．二元一次方程和一次函数的关系．2．能根据一次函数的图象求二元一次方程组的近似解．三．探索新知：（一）自主探究(1) 方程x +y =5的解有多少个？写出其中几个？(2)在直角坐标系中分别描出以这些解为坐标的点，它们在一次函数y =5－x 的图象上吗？(3)在一次函数y =5－x 的图象上任取一点，它的坐标适合方程x +y =5吗？(4)以方程x +y =5的解为坐标的所有点组成的图象与一次函数y =5－x 的图象相同吗？通过解决以上问题你发现什么：（二）完成课本P238做一做解方程组 ⎩⎨⎧=-=+125y x y x通过解决以上问题你发现什么：感悟与思考：通过本课的学习旨在揭示 之间的对应关系，从而引出了二元一次方程组的图象解法，同时也建立了“数”——二元一次方程组与“形”——函数图象之间的对应关系，培养了同学们初步的数形结合的意识和能力．(三).完成课本P239例1代数解法：（四）P240随堂练习四．拓展与探究：1.你能用作图象的方法解以下方程吗？试一试你能有几种方法。

-2x+4 = 432 x 代数解法：2.有一组数同时适合方程x+y=2和x+y=5吗？有一组数同时适合方程x+y=2和2x+2y=10吗？有一组数同时适合方程x+y=2和2x+y=4吗？做一做想一想你会发现一个有趣的现象。

五．检测反馈：1.方程2x-y=2的解有 个，用含x 的代数式表示y 为 。

此时y 是x 的 函数。

2.函数y=-2x+1与y=3x-9的图像的交点坐标为 ，这对数是方程组 的解。

3.已知直角坐标系中有A （1，4）B （2，3）C （2，-1）D （-1，1）四点，则经过A 、C 两点的直线与经过B 、D 两点的直线的交点坐标可看作是方程组 的解4.若一次函数y=-x+a 与y=x+b 两图像的交点为(m ，8)，则a+b=5.若方程组x+y=2 无解，则在同一直角坐标系中直线y=--x+2与y=-x+23必定（ ） 2x+2y=3（A ）相交 （B ）平行 （C ）重合 （D ）无法判断6.用图像法解方程组 x-y=3x+2y=--37.（1）在同一直角坐标系中作出一次函数y=x+2与y=x-3的图像（2）两者的图像之间有何关系？(3) 你能找出一组数同时适合方程x-y=-2和x-y=3吗？这能否说明方程组 x-y=-2x-y=3的解的情况8.已知在直坐标系中，直线L 1 经过点 (2,3)和 (-1,--3), 直线L 2经过原点且与直线L 1交与点(-2,a)。

☆ 高新一中八年级数学自学导案（18）一次函数应用专题 1 课题： 一次函数应用专题 第一部分：题型举例 一. 一次函数图象的应用 由函数图象解决实际问题的关键是读图、识图，要弄清函数图象上点的意义.图象上点的横坐标反映函数自变量的取值，纵坐标反映对应的函数值. 例1、 甲、乙两个工程队分别同时开挖两段河渠，所

挖河渠的长度my与挖掘时间hx之间的关系如图1所示，请根据图象所提供的信息解答下列问题： ⑴乙队开挖到30m时，用了 h． 开挖6h时甲队比乙队多挖了 m； ⑵请你求出：①甲队在06x≤≤的时段内，y与x之间的函数关系式；②乙队在26x≤≤的时段内，y与x之间的函数关系式； ⑶当x为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？ 分析:从图象观察可知,甲队在06x≤≤的时段内为正比例函数,故根据图象和点(6,60)就可以求得解析式.而乙队在26x≤≤的时段内为一次函数图象,故根据图象和点(2,30)和(6,50)就可以求得解析式.再根据y相等得到的关于x的方程求得第（3）⑶问. 解：⑴2，10； ⑵设甲队在06x≤≤的时段内y与x之间的函数关系式为1ykx，由图可知，函数图象过点(660)，，1660k，解得110k，10yx． 设乙队在26x≤≤的时段内y与x之间的函数关系式为2ykxb，由图可知，函数图象过点(230)(650)，，，，22230650kbkb，．解得2520.kb，520yx． ⑶由题意，得10520xx，解得4x（h）．当x为4h时，甲、乙两队所挖的河渠长度相等． 点拨:这道题考查的是函数关系,要求从已知函数图象中获取信息,求出函数值、函数表达式并解答相应的问题.设置了这样一个问题情景后，把两工程队的开挖长度与时间的关系用图象直观地反映出来，更容易理解两个变量间的函数关系以及函数关系的表示，在解决实际问题的过程中考查了对“双基”的理解和掌握.有助于改变对知识过分形式化的记忆和理解，克服单纯记忆知识和机械操作的倾向. 乙 60 50