交直流电路的计算公式
- 格式:doc
- 大小:225.31 KB
- 文档页数:6
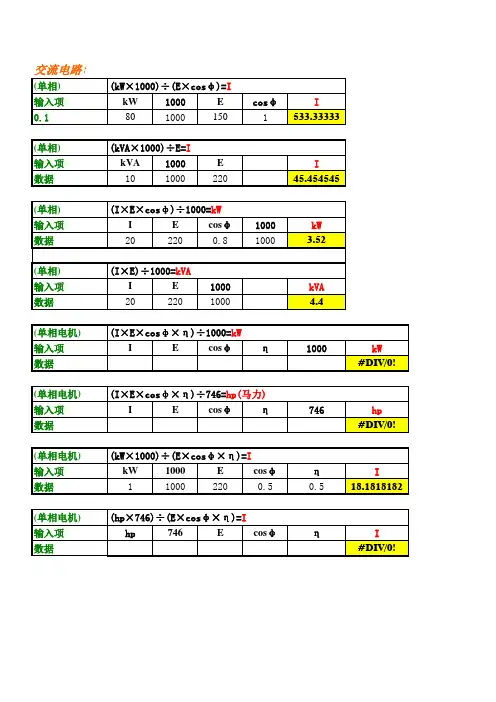



【物理知识点】电功率所有计算公式一、电功率计算公式1、在纯直流电路中:P=UI、P=I2R、P=U2/R。
2、在单相交流电路中:P=UIcosφ。
3、在对称三相交流电路中:P=√3UIcosφ。
二、欧姆定律部分1.I=U/R(欧姆定律:导体中的电流跟导体两端电压成正比,跟导体的电阻成反比)。
2.I=I1=I2=…=In(串联电路中电流的特点:电流处处相等)。
3.U=U1+U2+…+Un(串联电路中电压的特点:串联电路中,总电压等于各部分电路两端电压之和)。
4.I=I1+I2+…+In(并联电路中电流的特点:干路上的电流等于各支路电流之和)。
5.U=U1=U2=…=Un(并联电路中电压的特点:各支路两端电压相等。
都等于电源电压)。
6.R=R1+R2+…+Rn(串联电路中电阻的特点:总电阻等于各部分电路电阻之和)。
7.1/R=1/R1+1/R2+…+1/Rn(并联电路中电阻的特点:总电阻的倒数等于各并联电阻的倒数之和)。
8.R并=R/n(n个相同电阻并联时求总电阻的公式)。
9.R串=nR(n个相同电阻串联时求总电阻的公式)。
10.U1:U2=R1:R2(串联电路中电压与电阻的关系:电压之比等于它们所对应的电阻之比)。
11.I1:I2=R2:R1(并联电路中电流与电阻的关系:电流之比等于它们所对应的电阻的反比)。
三、电功计算公式W=UIt=Pt(适用于所有电路);对于纯电阻电路可推导出:W=I2Rt=U2t/R。
①串联电路中常用公式:W=I2Rt,W1:W2:W3:…Wn=R1:R2:R3:…:Rn。
②并联电路中常用公式:W=U2t/R,W1:W2=R2:R1。
③无论用电器串联或并联。
计算在一定时间所做的总功常用公式W=W1+W2+…Wn。
四、电功率1.电功率计算公式:P=UI=W/t(适用于所有电路)。
对于纯电阻电路可推导出:P=I2R=U2/R。
①串联电路中常用公式:P=I2R,P1:P2:P3:…Pn=R1:R2:R3:…:Rn。
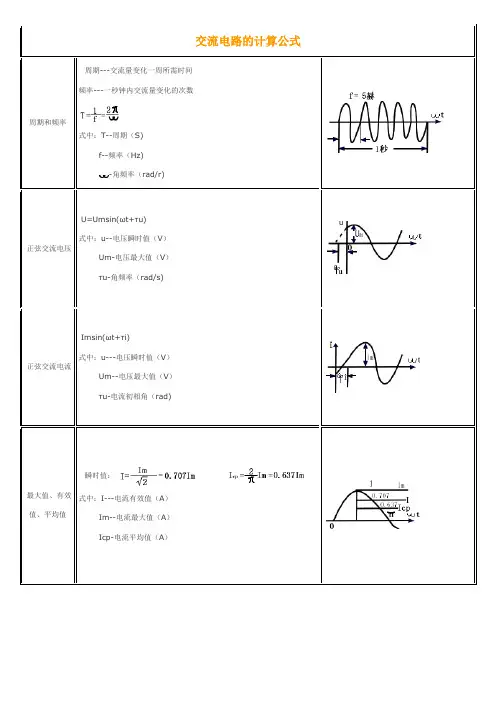
交流电路的计算公式周期和频率周期---交流量变化一周所需时间频率---一秒钟内交流量变化的次数式中:T--周期(S)------f--频率(Hz)-------角频率(rad/r)正弦交流电压U=Umsin(ωt+τu)式中:u--电压瞬时值(V)------Um-电压最大值(V)------τu-角频率(rad/s)正弦交流电流Imsin(ωt+τi)式中:u---电压瞬时值(V)------Um--电压最大值(V)------τu-电流初相角(rad)最大值、有效值、平均值瞬时值:式中:I---电流有效值(A)------Im--电流最大值(A)------Icp-电流平均值(A)纯电阻电路瞬时值:u=Umsin(ωt+τu) ----i=Imsin(ωt+τu)最大值Um=RIm ,有效值U=RI有功功率:无功功率:Q=0初相角τu=τi,u与i相同纯电感电路瞬时值:ul=Ulmsin(ωt-0℃) i=Ilmsin(ωt-90℃) 最大值Ulm=X l I lm有效值Ul=X l I l式中:XL=ωL=2πfL有效功率PL=0无功功率Q=U L I L=X L I L初相角τu=0℃,τi=-90℃,UL超前于iL90℃纯电容电路瞬时值:Uc=Ucmsin(ωt+0℃) --i=Icmsin(ωt-90℃) 最大值:Ucm=Xc I cm有效值:Uc=Xc I c式中:有功功率:Pc=0无功功率:Qc=UcIc=XcFc初相角τu=0℃,τi=90℃,Uc滞后于ic90℃RLC并联电阻有效值:I=UY导纳:当bL=bc时,Y=g,I与U同相,称为并联谐振电纳b=bL-bc当bL=0时,成为RC并联电路当bc=0时,成为RL并联电路有功功率P=UIcosτ无功功率Q=UIsinτ视在功率功率因数cosτ=等效阻抗与等效导纳变换电阻电纳等效阻抗与等效导纳变换串联顺接L=L1+L2+2M 反接L=L1+L2-2M 并联式中:L---总电感------M---互感Y-△阻抗变换Y-△Y-△阻抗变换当Zab=Zbc=Zca=Z△,时直流电路计算公式欧姆定律 1、无源支路:式中:U----支路端电压(V)------I----支路电流(A)------R----支路电阻(Ω)------±---U与I同向取+号,否则取-号图A,图B欧姆定律 2、有源支路式中:E----支路电动势(V)U、I、R与无源支路同-----±U与I向、E与I同向取+号,否则取一号图A。

交流与直流电流换算公式解释说明以及概述1. 引言1.1 概述交流电流和直流电流是电学中重要的两种电流形式。
在现代社会,无论是家庭用电、工业生产还是通讯系统,我们都离不开这两种电流。
了解交流与直流电流之间的差异以及它们的换算公式对于我们正确认识和应用电学原理具有重要意义。
1.2 文章结构本文将首先介绍交流电流和直流电流的区别与特点,包括它们的定义、特点及应用场景。
接着,我们会详细阐述交流电流和直流电流的换算公式。
在交流部分,我们将讨论峰峰值、平均值和有效值之间的关系,并给出计算方法;同时,也会介绍脉冲信号的表示方法与相应的换算公式。
在直流部分,我们将重点讲解线性负载下欧姆定律的计算方法,并探讨非线性负载情况下的换算公式及实际应用示例。
最后,在结论部分我们将总结交直流换算公式并归纳其应用范围。
1.3 目的本文旨在深入介绍交直流电流的区别、特点和应用,并详细讲解两者之间的换算公式,以帮助读者更好地理解交直流电流的本质和计算方法。
通过阅读本文,读者将能够掌握交直流电流换算公式的推导过程和实际应用场景,并能够灵活运用这些公式解决相关问题。
同时,本文也可以作为学习电学基础知识和深入研究交直流电流转换桥梁,进一步拓宽读者对于电学领域的认识和理解。
2. 交流电流和直流电流的区别与特点2.1 交流电流的定义和特点:交流电流指的是电荷在导体中来回移动,其方向和大小都会随着时间而变化。
交流电流的特点是:- 方向变化:在一个完整的周期内,交流电流会改变方向多次。
这是因为交流电源(如发电机)产生的电压具有周期性,从正值到负值再到正值。
- 幅度变化:同样,在一个周期内,交流电流的幅度也会随着时间不断变化,从最大正值到最小值再到最大负值。
此外,根据频率的不同,可以将交流电分为低频、中频和高频三类。
低频交流电常用于家庭用电和工业应用中,而高频交流电常用于通信和无线传输等领域。
2.2 直流电流的定义和特点:相比之下,直流电流(Direct Current, DC)指的是沿着一个固定方向持续不变的电荷运动。

电功率计算公式电功率计算公式一、电功率计算公式:1、在纯直流电路中:P=UI,P=I²R,P=U²/R;式中:P---电功率(W),U---电压(V),I---电流(A),R---电阻(Ω)。
2、在单相交流电路中:P=UIcosφ式中:cosφ---功率因数,如白炽灯、电炉、电烙铁等可视为电阻性负载,其中cosφ=1则P=UI;U、I---分别为相电压(220V)、相电流。
3、在对称三相交流电路中,不论负载的连接是哪种形式,对称三相负载的平均功率都是:P=√3UIcosφ式中:U、I---分别为线电压(380V)、线电流。
cosφ---功率因数,若为三相阻性负载,如三相电炉,cosφ=1则P=√3UI;若为三相感性负载,如电动机、压缩机、继电器、日光灯等等。
cosφ=0.7~0.85,计算取值0.75。
4、说明:阻性负载:即和电源相比当负载电流负载电压没有相位差时负载为阻性(如负载为白炽灯、电炉等)。
通俗一点讲,仅是通过电阻类的元件进行工作的纯阻性负载称为阻性负载。
感性负载:通常情况下,一般把带电感参数的负载,即符合电压超前电流特性的负载,称为感性负载。
通俗地说,即应用电磁感应原理制作的大功率电器产品。
二、欧姆定律部分1、I=U/R(欧姆定律:导体中的电流跟导体两端电压成正比,跟导体的电阻成反比)2、I=I1=I2=…=In(串联电路中电流的特点:电流处处相等)3、U=U1+U2+…+Un(串联电路中电压的特点:串联电路中,总电压等于各部分电路两端电压之和)4、I=I1+I2+…+In(并联电路中电流的特点:干路上的电流等于各支路电流之和)5、U=U1=U2=…=Un(并联电路中电压的特点:各支路两端电压相等。
都等于电源电压)6、R=R1+R2+…+Rn(串联电路中电阻的特点:总电阻等于各部分电路电阻之和)7、1/R=1/R1+1/R2+…+1/Rn(并联电路中电阻的特点:总电阻的倒数等于各并联电阻的倒数之和)8、R并=R/n(n个相同电阻并联时求总电阻的公式)9、R串=nR(n个相同电阻串联时求总电阻的公式)10、U1:U2=R1:R2(串联电路中电压与电阻的关系:电压之比等于它们所对应的电阻之比)11、I1:I2=R2:R1(并联电路中电流与电阻的关系:电流之比等于它们所对应的电阻的反比)二、电功率部分12、P=UI(经验式,适合于任何电路)13、P=W/t(定义式,适合于任何电路)14、Q=I2Rt(焦耳定律,适合于任何电路)15、P=P1+P2+…+Pn(适合于任何电路)16、W=UIt(经验式,适合于任何电路)17、P=I2R(复合公式,只适合于纯电阻电路)18、P=U2/R(复合公式,只适合于纯电阻电路)19、W=Q(经验式,只适合于纯电阻电路。

电压电流计算公式电压和电流是电学中两个重要的物理量,它们之间存在着密切的关系。
在电路中,通过电压和电流的计算公式,我们可以准确地计算出电压和电流的数值,进而分析和解决实际电路中的问题。
我们来看一下电压的计算公式。
电压(V)的定义是单位正电荷所具有的电势能,即电压等于电势差。
在直流电路中,电压的计算公式为V=IR,其中V表示电压,I表示电流,R表示电阻。
这个公式告诉我们,电压与电流成正比,当电阻不变时,电压与电流呈线性关系。
换句话说,电压的大小取决于电流的大小和电阻的大小。
接下来,让我们来了解一下电流的计算公式。
电流(I)的定义是单位时间内通过导体横截面的电荷量,即电流等于单位时间内通过的电荷量。
在直流电路中,电流的计算公式为I=V/R,其中I表示电流,V表示电压,R表示电阻。
这个公式告诉我们,电流与电压成正比,与电阻成反比。
当电压不变时,电流与电阻呈反比关系;当电阻不变时,电流与电压呈正比关系。
通过电压和电流的计算公式,我们可以解决一些实际电路中的问题。
例如,当我们知道电压和电阻的数值时,可以通过电流的计算公式求解电流的数值。
同样地,当我们知道电流和电阻的数值时,可以通过电压的计算公式求解电压的数值。
这些计算公式可以帮助我们更好地理解和分析电路中的电压和电流的变化规律,进而优化电路设计和故障排除。
除了直流电路,交流电路中也存在着电压和电流的计算公式。
在交流电路中,电压和电流是随时间变化的。
对于正弦交流电路,电压和电流的关系可以用复数形式表示。
在这种情况下,电压和电流的计算公式为U=IZ,其中U表示电压,I表示电流,Z表示阻抗。
阻抗是交流电路中电阻和电抗的综合体现,它的大小和相位角决定了电流和电压之间的关系。
总结起来,电压和电流的计算公式在电学中起着至关重要的作用。
通过这些公式,我们可以准确地计算出电压和电流的数值,分析和解决实际电路中的问题。
无论是直流电路还是交流电路,电压和电流的计算公式都是电学学习中的基础知识,掌握它们对于电路设计和故障排除都具有重要意义。

电功率计算公式:在纯直流电路中:P=UI P=I²R P=U²/R 式中:P---电功率(W),U---电压(V),I----电流(A),R---电阻(Ω). 在单相交流电路中:P=UIcosφ式中:cosφ---功率因数, 如白炽灯、电炉、电烙铁等可视为电阻性负载,其cos φ=1 则P=UIU、I---分别为相电压、电流。
在对称三相交流电路中,不论负载的连接是哪种形式,对称三相负载的平均功率都是:P=√3UIcosφ式中:U、I---分别为线电压、线电流。
cosφ---功率因数,若为三相阻性负载,如三相电炉,cosφ=1则P=√3UI。
一、P=UI的两个同胞兄弟及其应用功率计算公式P=UI联合欧姆定律可患上到以下两个公式:一、由欧姆定律可知,将其代入便患上到电功率的熬头个兄弟公式:(推论:在电压相等的环境下,用电器消耗的功率与其电阻成反比)2、P=I2R同理,可将U=IR代入P=UI患上到电功率的第二个兄弟公式:P=I2R(推论:在电流相等的环境下,用电器消耗的功率与其电阻成正比)导出公式、P=I2R与公式P=UI就像是三个同胞兄弟,各有自已的独特之处,若能根据实际环境灵活选择,将给我们解题带来泼天的利便性,大大节省时间。
例一、把规格为“220V,60W”和“220V,40W”的甲、乙两只灯胆串联后接在220伏的电路中,问哪个灯胆更亮些?分析:灯胆的亮度由灯胆事情时的实际功率来决议,以上三个公式都可用来计算实际功率,选择哪个更利于我们解题与电路的连接方式有着很大的关系。
在一般环境下:⑴.串联电路中,因为电流到处相等,以是用P=I2R分析比较各用电器的功率较为利便;(2).并联电路中,因为各并联电路两真个电压相等,以是用分析比较各用电器的功率较为利便.本题选择公式举行分析很快就能够获悉,两只灯胆的实际功率与电阻成正比(串联电路中,流过两灯胆电流相等),上面的需要解答的题目就转化为比较甲、乙两只灯胆的电阻巨细关系了。

交流变直流的计算公式
交流电与直流电是两种不同类型的电流。
交流电是指电流的极性和电压的方向在规定的时间间隔内交替变化,而直流电则是指电流的极性和电压方向保持不变。
在某些情况下,我们需要将交流电转换为直流电,如电子设备的供电等。
此时,我们需要了解交流变直流的计算公式。
交流变直流的计算公式为:
Vdc = Vrms × 1.414
其中,Vdc表示直流电压,Vrms表示交流电压的有效值,1.414为常数。
例如,若一台设备需要5V的直流电源,而提供的电源是220V的交流电,我们可以使用上述公式计算得到直流电压的值为:
Vdc = 220V × 1.414 = 311.08V
当然,这个结果并不是我们需要的,因为它远远高于我们所需要的5V电源。
在实际使用中,我们需要通过电子元器件(如变压器、整流器等)进行变换和调整,使得交流电转换成我们需要的直流电源。
在此,还需要注意的是,交流电的电压分为峰值电压、峰峰值电压、平均值电压和有效值电压等。
而直流电的电压则只有一个值。
因此,在进行交流变直流的计算时,需要根据实际情况选择正确的电压值进行计算。
总的来说,交流变直流的计算公式为Vdc = Vrms × 1.414。
在实际使用中,需要根据实际情况进行电路设计和元器件的选择,以达
到所需要的直流电源。

交直流电路的计算公式1.电阻电路计算公式:1.1电阻电流公式:I=V/R1.2电阻电压公式:V=I*R1.3电阻功率公式:P=I^2*R=V^2/R2.电感电路计算公式:2.1 电感电流公式:I = (V/Z)*sin(θ)2.2 电感电压公式:V = (I*Z)*sin(θ)其中,Z是电感的阻抗,θ是电路中电感和电压的相位差。
3.电容电路计算公式:3.1 电容电流公式:I = (V/Z)*cos(θ)3.2 电容电压公式:V = (I*Z)*cos(θ)其中,Z是电容的阻抗,θ是电路中电容和电压的相位差。
4. Ohm定律:U = I*ROhm定律是用来计算电压、电流和电阻之间关系的基本公式。
5.电功率计算公式:5.1 交流电功率公式:P = U*I*cos(θ)5.2直流电功率公式:P=U*I其中,θ是交流电路中电流和电压的相位差。
6.电源电流计算公式:6.1 交流电源电流公式:I = P/(U*cos(θ))6.2直流电源电流公式:I=P/U7.电源的电流、电压和功率之间的关系:7.1 交流电源的功率公式:P = U*I*cos(θ)7.2直流电源的功率公式:P=U*I8.等效电阻计算公式:8.1串联电阻的等效电阻公式:R=R1+R2+R3+...8.2并联电阻的等效电阻公式:1/R=1/R1+1/R2+1/R3+...9.并联电容的等效电容计算公式:C=C1+C2+C3+...10.串联电感的等效电感计算公式:L=L1+L2+L3+...这些公式可以用来计算交直流电路中各种参数之间的关系,帮助电工工程师分析和设计电路,以及故障检修和电路优化。
总视在功率计算公式
总视在功率是指电路中所有元件(包括电阻、电感和电容)消耗的功率总和。
总视在功率的计算公式如下:
在交流电路中,总视在功率P(单位为瓦特,W)可以通过以下公式计算:
P = VIcosφ。
其中,V表示电压(单位为伏特,V),I表示电流(单位为安培,A),φ表示电压和电流的相位差。
在直流电路中,总视在功率P(单位为瓦特,W)可以通过以下公式计算:
P = VI.
其中,V表示电压(单位为伏特,V),I表示电流(单位为安培,A)。
这些公式可以帮助我们计算电路中的总视在功率,从而更好地了解电路的能量消耗情况。
需要注意的是,这里的电压和电流都是有效值。
电压电流功率电量计算公式一、基本公式。
1. 功率(P)与电压(U)、电流(I)的关系。
- 对于直流电路和纯电阻交流电路,功率的计算公式为P = UI。
- 推导:根据电功W=UIt(电功等于电压、电流和时间的乘积),功率P=(W)/(t),将W = UIt代入可得P=(UIt)/(t)=UI。
2. 电量(Q)与电流(I)、时间(t)的关系。
- 电量的计算公式为Q = It。
- 这表示在一段时间t内,通过导体横截面的电量等于电流强度与时间的乘积。
3. 由P = UI和Q = It推导其他关系。
- 由I=(Q)/(t),将其代入P = UI可得P = U(Q)/(t),进一步变形为Q=(Pt)/(U)。
- 如果已知功率P和电阻R(对于纯电阻电路I = (U)/(R),即U = IR),将U = IR代入P = UI可得P=I× IR = I^2R,再结合Q = It,可得Q=(Pt)/(I^2)R。
- 同样,由I=(U)/(R)可得P=frac{U^2}{R},再结合Q = It和I=(U)/(R),可得Q=(PtR)/(U^2)。
二、在不同电路中的应用示例。
1. 纯电阻电路。
- 例如,一个电阻R = 10Ω的用电器,两端电压U = 220V。
- 首先根据I=(U)/(R)计算电流I=(220V)/(10Ω)=22A。
- 然后根据P = UI计算功率P = 220V×22A = 4840W。
- 如果该用电器工作t = 1h = 3600s,根据Q = It计算电量Q = 22A×3600s = 79200C(库仑)。
2. 非纯电阻电路(如电动机电路)- 对于电动机,输入功率P_入=UI,但电动机消耗的电能一部分转化为机械能,一部分转化为内能(P_热=I^2R),输出的机械功率P_机=P_入-P_热。
- 例如,电动机两端电压U = 220V,电流I = 2A,线圈电阻R = 5Ω。
交流转直流电流计算公式咱们在生活和学习中,经常会碰到电流的问题。
电流有交流和直流之分,今天咱们就来好好聊聊交流转直流电流的计算公式。
先来说说啥是交流电流和直流电流。
交流电流呢,就像是个调皮的孩子,一会儿跑快一会儿跑慢,方向还不停地变。
比如说咱们家里用的市电,就是交流电流。
而直流电流呢,就比较老实啦,它总是朝着一个方向跑,速度也比较稳定。
像咱们的电池提供的电流,就是直流电流。
那为啥要把交流转成直流呢?这就好比你有一堆乱蹦乱跳的弹珠(交流电流),你想让它们规规矩矩地排成一排(直流电流),这样用起来更方便。
比如说,咱们的手机充电器,就是把交流市电转成直流给手机电池充电的。
那交流转直流电流咋计算呢?这就得提到一个重要的东西——整流电路。
整流电路就像是个神奇的魔法盒子,能把交流电流变成直流电流。
常见的整流电路有半波整流和全波整流。
咱们先说半波整流。
半波整流就像是个小气鬼,只让交流电流的一半通过。
它的电流平均值可以用这个公式算:I(av) = 0.45×I(m) 。
这里的 I(av) 就是直流电流的平均值,I(m) 是交流电流的峰值。
比如说,交流电流的峰值是 10 安培,那通过半波整流后,直流电流的平均值就是 0.45×10 = 4.5 安培。
再来说说全波整流。
全波整流可比半波整流大方多了,它让交流电流的正半周和负半周都通过。
它的电流平均值是:I(av) = 0.9×I(m) 。
假设交流电流的峰值还是 10 安培,那全波整流后的直流电流平均值就是 0.9×10 = 9 安培。
我记得有一次,我在家里修一个小电器。
我发现它的电源部分出了问题,交流转直流没弄好。
我就拿着万用表,一边对照着书上的公式,一边测量电流。
那时候可紧张了,就怕修不好。
最后经过一番折腾,还真让我给算对了,修好了那个小电器,心里那叫一个美!总之,交流转直流电流的计算并不难,只要咱们搞清楚用的是哪种整流电路,记住对应的公式,再加上实际测量和一点点耐心,就能轻松搞定啦!希望大家通过今天的分享,对交流转直流电流的计算公式有更清楚的了解,以后遇到相关的问题都能迎刃而解!。
一次额定电流计算值公式和计算方法
一次额定电流计算值可以使用下列公式和计算方法,具体取决于具体的电路和设备情况:
1. 对于直流电路:
一次额定电流(I) = 感性负载电流(I) + 电阻负载电流(I)+ 起动电流(I) + 安全系数(如果需要)
2. 对于交流电路:
一次额定电流(I) = 短时热电流(Ith)/(√3 * 系统电压(U) * 安全系数)
其中,安全系数是为了确保设备能够在额定电流下正常运行,并应根据实际情况进行选择。
需要注意的是,上述公式只是一般情况下的计算方法,实际情况可能会存在其他因素和修正系数,在具体计算时应根据设备规格书和相关标准进行详细的分析和计算。
如何计算电流的大小电流是电荷通过导体携带能量的量度,是电路中非常重要的物理量。
在电路分析和设计中,准确计算电流的大小是至关重要的。
本文将介绍如何计算电流的大小以及相关的计算公式。
一、电流的定义电流是单位时间内通过导体某一横截面的电荷量,通常用字母I表示。
其单位是安培(A)。
电荷量的符号与所携带电荷的载流子的电荷性质相关,正电流表示正电荷的流动,负电流表示负电荷的流动。
二、电流的计算公式根据电流的定义,我们可以得到电流的计算公式:I = Q / t其中,I表示电流,Q表示通过横截面的电荷量,t表示时间。
三、直流电路中电流的计算在直流电路中,电流值可以通过欧姆定律来计算,欧姆定律表达了电流、电压和电阻之间的关系:I = V / R其中,V表示电压,R表示电阻。
四、并联电阻中电流的计算当电路中存在并联电阻时,可以使用基尔霍夫定律来计算电流的大小。
基尔霍夫定律分为节点电流定律和回路电压定律。
1. 节点电流定律节点电流定律表明,在任意一个节点处,进入该节点的电流之和等于离开该节点的电流之和。
例如,对于一个并联电路中的节点A,从节点A进入的总电流等于从节点A离开的总电流:I1 + I2 + ... + In = Ia + Ib + ... + In2. 回路电压定律回路电压定律表明,在任意一个闭合回路中,电压上升之和等于电压下降之和。
例如,在一个并联电路中的闭合回路ABCD中,电压源的电压与电阻上的电压之和等于零:Va + Vb + Vc + ... + Vn = 0根据基尔霍夫定律,可以推导出电流的计算公式。
在并联电路中,电阻之间的电压相等,因此可以利用电压和电阻来计算电流的大小:I1 = V / R1I2 = V / R2...In = V / RnI = I1 + I2 + ... + In = (V / R1) + (V / R2) + ... + (V / Rn) = V × (1 / R1 +1 / R2 + ... + 1 / Rn)五、串联电阻中电流的计算当电路中存在串联电阻时,电流在各个电阻中的值相等,可以通过Ohm's Law计算电流的大小:I = V / R其中,I表示电流,V表示电压,R表示串联电阻的总阻值。
交流电功率计算公式是什么?
交流电功率计算公式:
交流电是要考虑功率因数的,P=UIcosq,这是单相交流电。
对于三相平衡电路来说,要乘以根号3,U、I为线电压与线电流的有效值。
交流电功率计算方法
功率(直流)=电流*电压
功率(单相交流)=电压*电流*功率因数
功率(三相交流)=电压*电流*功率因数*1.732
注意三相交流和380供电是两个概念:
如果用电设备的电源线是3根线(不包含接地线)的话,即该设备为三相交流设备。
如果用电设备的电源线是2根线(不包含接地线),即使使用的是380V供电的三相电源供电,该设备仍然为单相交流设备P=UI=I^2*RU——加载导体两端的电压,单位是伏[特]I——导体中的电流,单位是安{培]R——负载电阻,单位是欧[姆]P——电功率,单位是瓦[特]。
交流电路的计算公式:
周期和频率
周期---交流量变化一周所需时间频率---一秒钟内交流量变化的次数
式中:T--周期(S)
------f--频率(Hz)
-------角频率(rad/r)
正弦交流电压
U=Umsin(ωt+τu)
式中:u--电压瞬时值(V)------Um-电压最大值(V)------τu-角频率(rad/s)
正弦交流电流
Imsin(ωt+τi)
式中:u---电压瞬时值(V)------Um--电压最大值(V)------τu-电流初相角(rad)
最大值、有效值、平均值
瞬时值:
式中:I---电流有效值(A)------Im--电流最大值(A)------Icp-电流平均值(A)
纯电阻电路瞬时值:u=Umsin(ωt+τu) ----i=Imsin(ωt+τu)
最大值Um=RIm ,
有效值U=RI
有功功率:
无功功率:Q=0
初相角τu=τi,u与i相同
纯电感电路瞬时值:ul=Ulmsin(ωt-0℃) i=Ilmsin(ωt-90℃) 最大值Ulm=X l I lm
有效值Ul=X l I l
式中:XL=ωL=2πfL
有效功率PL=0
无功功率Q=U L I L=X L I L
初相角τu=0℃,τi=-90℃,UL超前于iL90℃
纯电容电路
瞬时值:Uc=Ucmsin(ωt+0℃) --i=Icmsin(ωt-90℃) 最大值:Ucm=Xc I cm
有效值:Uc=Xc I c
式中:
有功功率:Pc=0
无功功率:Qc=UcIc=XcFc
初相角τu=0℃,τi=90℃,Uc滞后于ic90℃
RLC并联电阻
有效值:I=UY
导纳:
当bL=bc时,Y=g,I与U同相,称为并联谐振电纳b=bL-bc
当bL=0时,成为RC并联电路
当bc=0时,成为RL并联电路
有功功率P=UIcosτ
无功功率Q=UIsinτ
视在功率
功率因数cosτ=
等效阻抗与等
效导纳变换
电阻
电纳
等效阻抗与等效导纳变换
串联
顺接L=L1+L2+2M 反接L=L1+L2-2M 并联
式中:L---总电感
------M---互感
Y-△阻抗变换
Y-△
Y-△阻抗变换
当Zab=Zbc=Zca=Z△,时
直流电路计算公式
欧姆定律 1、无源支路:
式中:U----支路端电压(V)
------I----支路电流(A)
------R----支路电阻(Ω)
------±---U与I同向取+号,否则取-号
图A,图B
欧姆定律 2、有源支路
式中:E----支路电动势(V)U、I、R与无源支路同-----±U与I向、E与I同向取+号,否则取一号
图A。
图B
欧姆定律 3、全电路
式中:E1、E2--回路电动势(V)
------I-------回路电流(A)
------ΣR-----回路电子之和(Ω)
------±------E1、E2与I同向取+否则取-号
导体电阻
(Ω)
式中:R---导体直流电阻(Ω)
------ι--导体长度(M)
------S---导体载面积(CM)
------ρ--导体电阻率(Ω.CM/M)
导体电阻与温度关系
(Ω)
式中:---导体t℃时的电阻(Ω)
---------导体20℃时的电阻(Ω)
-------a----导体的电阻温度系数(1/℃)-------t----温度(℃)
电导与电导
率式中:G---电导(S)---------电导率(A)---------电阻率(S)
功率式中:P--功率(W)
------U--电压(V)
------I--电流(A)
------R--电阻(Ω
I不变(电阻串联)时,P与R成正比U不变(电阻并联)时,P与R成反比
电阻串、并、
复联
串联:电阻:
电导:
当=0时,R2上的分电压式中:Uab--ab两端端电压
--分压比
电阻串、并、
复联
并联电阻:电导:
当=00时,R2上的分电流:
式中:Iab---流经ab的端电流分流比
电阻串、并、
复联
复联电阻:电导:
电容器串、并、复联串联:当n个相待的C0串联时当C3被短路时,C2上的分电压
式中:Uab----ab两端端电压电容分压比
电容器串、并、复联
并联:
当n个相同等的CO并联时C=nco
电容器串、并、复联
并联:
当n个相同等的CO并联时C=nco
屏蔽线圈串、
并联的等效电
感
串联
屏蔽线圈串、
并联的等效电
感
并联
电池串、并联
串联E=E1+E2+En ------I=I1+I2+In
r1、r2分别为电池的内阻当n个电池的电动势均为E0,内阻均为r0
电池串、并联
并联
r1、r2分别为电池的内阻。
每个电池的电动势和内阻必须相等才能并联,否则电池之间产生电流,消耗能量。