五年级下册分数简便计算

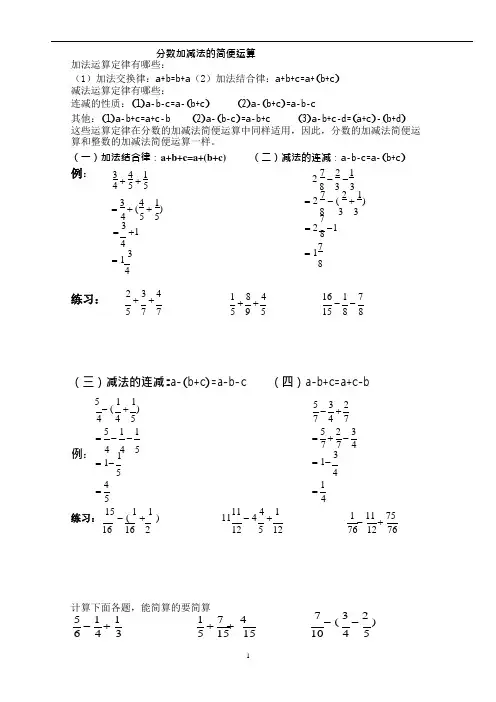
分数加减法的简便运算加法运算定律有哪些：（1）加法交换律：a +b =b +a （2）加法结合律：a +b +c =a +(b +c )减法运算定律有哪些：连减的性质：(1)a -b -c =a -(b +c ) (2)a -(b +c )=a -b -c 其他：(1)a -b +c =a +c -b (2)a -(b -c )=a -b +c (3)a -b +c -d =(a +c )-(b +d ) 这些运算定律在分数的加减法简便运算中同样适用，因此，分数的加减法简便运 算和整数的加减法简便运算一样。

（一）加法结合律：a+b+c=a+(b+c)（二）减法的连减：a -b -c =a -(b +c )例：3 +4 + 1 45 5 2 7 - 2 - 1 8 3 3 = 3 + 4 ( 4 + 1) 5 5 = 2 7 - ( 2 + 1) 8 3 3 7 = 3 +1 = 2 -1 8 4 = 1 3 4练习：2 +3 + 41 + 8 + 4 = 17 816 - 1 - 7 5 7 75 9 515 8 8（三）减法的连减:a -(b +c )=a -b -c（四）a -b +c =a +c -b5- ( 1 + 1) 4 4 5 = 5 - 1 - 1 例： 4 4 5= 1- 15 = 4 55 - 3 + 2 7 4 7 = 5 + 2 - 3 7 7 4 = 1- 34 = 1 4练习： 15 - ( 1 + 1)1111- 4 4 + 1 1 - 11 + 75 16 16 212 5 1276 12 76计算下面各题，能简算的要简算 5 - 1 + 1 1 + 7 + 4 7 - ( 3 - 2) 6 4 3 5 15 1510 4 5米的木头截去 和截去 米，剩下的部分不一样长。

（10 - 5 + 14 - 2 + 9 3 - 7 - 9 9 6 613 9 132 16 16分数乘除法的简便运算（一）乘法结合律：a ×b ×c=a ×(b ×c)例： 5 ⨯ 3 ⨯ 47 8 15（二）乘法分配率：（a+b ）×c=a ×c+b ×ca ×c+b ×c=（a+b ）×c 例： （3 + 1）⨯ 30 （ 2 - 1）⨯ 271 ⨯ 99 + 99 ⨯ 6 5 6 3 97 717 3 173 3 54 变式题：5 × ＋5 ÷4× + ÷ 24 4 248 4 8 3计算下面各题，能简算的要简算。

人教版五年级下册数学课本中，分数简便计算是一个重要的知识点。

学生通过学习这一部分内容，不仅可以掌握基本的分数计算方法，还可以提高自己的数学思维能力。

下面将通过具体的内容和方法，来详细介绍该知识点。

一、分数的基本概念1. 分数的定义在数学中，分数是指一个正整数除以另一个正整数所得到的结果。

分数通常由一个分子和一个分母组成，分子表示被分的部分，分母表示总的份数。

2. 分数的大小比较分数的大小比较是分数运算中的基础知识。

一般来说，可以通过分数的分母大小进行比较。

分母相同的情况下，比较分子的大小；分母不同的情况下，可以通分后再比较。

二、分数的四则运算1. 分数的加法分数的加法是指将两个分数相加，首先需要将两个分数通分，然后将分子相加，分母保持不变。

2. 分数的减法分数的减法是指将一个分数减去另一个分数，同样需要将两个分数通分，然后将分子相减，分母保持不变。

3. 分数的乘法分数的乘法是指将两个分数相乘，可以直接将两个分数的分子相乘，分母相乘。

4. 分数的除法分数的除法是指将一个分数除以另一个分数，可以将除法转化为乘法，即将分数倒数后再进行乘法运算。

三、分数简便计算1. 分数的化简在进行分数运算时，通常需要将分数化简到最简形式，即分子和分母没有公共约数。

可以通过求最大公约数来化简分数。

2. 分数的混合运算在实际问题中，常常出现分数的混合运算，即包括加减乘除在内的多种运算。

对于这种情况，需要按照运算顺序进行计算，通常先进行括号内的运算，再进行乘除运算，最后进行加减运算。

3. 分数的转化分数可以转化为小数或百分数，这在实际问题中很常见。

转化为小数可以通过除法得到，转化为百分数则需要乘以100。

四、常见问题解析1. 如何判断一个数是否是分数？一个数是否是分数，可以通过它的表达形式来判断。

如果一个数可以表示为两个正整数的比值，那么它就是一个分数。

2. 分数的运算有什么特殊性？分数的四则运算与整数的四则运算有所不同，主要体现在通分和化简两个方面。

五年级数学分数简便计算简介分数是数学中一个非常重要的概念，在日常生活中也经常遇到。

对于五年级的学生来说，掌握分数的计算方法是非常关键的。

本文将介绍几种简便的方法，帮助五年级的学生更好地理解和计算分数。

一、分数的基本概念分数由分子和分母组成，分子表示被分割的数量，分母表示分割的份数。

分子在分数中位于分数线的上方，分母位于下方。

例如，对于分数 3/4，3是分子，4是分母。

3表示有3个等分后的单位，4表示被分割成4份。

二、相同分母的分数加减当分数的分母相同时，可以直接对分子进行加减运算，分母保持不变。

例如，计算 1/4 + 3/4：1/4 + 3/4 = 4/4 = 1同样，对于分数的减法也是类似的。

例如，计算 5/6 - 2/6：5/6 - 2/6 = 3/6 = 1/2三、不同分母的分数加减当分数的分母不同，需要先将分数的分母统一为相同的数，再进行加减运算。

1. 倍原分母法对于两个分数的分母 a 和 b，找到它们的最小公倍数（LCM），可以通过分别将 a 和 b 进行倍数扩展，使得最后的分母相同。

然后，对应扩展的分子进行加减运算。

例如，计算 2/3 + 1/4：首先，确定最小公倍数为 12，然后将分数的分母分别扩展为 12，得到：2/3 + 1/4 = 8/12 + 3/12 = 11/12同样，对于减法也是类似的。

2. 通分计算法另一种方法是使用通分计算法，即将两个分数按照最小公倍数进行扩展，然后进行加减运算。

例如，计算 1/2 + 2/3：首先，确定最小公倍数为 6，然后将分数的分子和分母分别扩展为通分后的数，得到：1/2 + 2/3 = 3/6 + 4/6 = 7/6可见，通分计算法和倍原分母法的结果是一样的。

四、分数的乘法和除法1. 分数的乘法分数的乘法需要将分子和分母分别进行相乘。

例如，计算 2/3 * 1/4：2/3 * 1/4 = 2 * 1 / 3 * 4 = 2/12 = 1/62. 分数的除法分数的除法需要将第一个分数的分子和第二个分数的分母相乘，第一个分数的分母和第二个分数的分子相乘。

五年级下册数学分数简便计算一、分数简便计算的基础：运算定律。

1. 加法交换律和结合律。

- 加法交换律：a + b=b + a。

在分数计算中同样适用，例如(1)/(3)+(2)/(5)=(2)/(5)+(1)/(3)。

- 加法结合律：(a + b)+c=a+(b + c)。

- 例：((1)/(4)+(1)/(3))+(2)/(3)=(1)/(4)+((1)/(3)+(2)/(3))=(1)/(4)+1 = 1(1)/(4)。

2. 乘法交换律、结合律和分配律。

- 乘法交换律：a× b = b× a。

如(2)/(3)×(3)/(4)=(3)/(4)×(2)/(3)。

- 乘法结合律：(a× b)× c=a×(b× c)。

- 例：((1)/(2)×(2)/(3))×(3)/(4)=(1)/(2)×((2)/(3)×(3)/(4))=(1)/(2)×(1)/(2)=(1)/(4)。

- 乘法分配律：a×(b + c)=a× b+a× c。

- 例：(1)/(2)×((1)/(3)+(1)/(4))=(1)/(2)×(1)/(3)+(1)/(2)×(1)/(4)=(1)/(6)+(1)/(8)=(4 + 3)/(24)=(7)/(24)。

- 乘法分配律的逆用：a× b+a× c=a×(b + c)。

- 例：(1)/(3)×(2)/(5)+(1)/(3)×(3)/(5)=(1)/(3)×((2)/(5)+(3)/(5))=(1)/(3)×1=(1)/(3)。

二、常见的分数简便计算类型。

1. 同分母分数的简便计算。

- 同分母分数相加或相减时，分母不变，分子相加减。

五年级下分数的简便计算《分数的简便计算，你会吗？》嘿，同学们！你们知道吗？在五年级下册的数学学习中，分数的简便计算可有意思啦！有一次上数学课，老师在黑板上写下了一道分数计算题：“3/4 + 7/8 - 1/2”。

好多同学一看就开始抓耳挠腮，嘴里嘟囔着：“哎呀，这可怎么算呀？”我也有点懵，心里想：这也太复杂了吧？这时候，老师笑了笑说：“同学们，别着急，咱们来看看怎么简便计算。

”老师就像一个神奇的魔法师，一下子就把难题变得简单了。

老师说：“咱们先把这些分数通分，找到它们分母的最小公倍数。

”我一听，恍然大悟，这不就像给不同尺码的鞋子找一个合适的盒子嘛！老师接着说：“4、8、2 的最小公倍数是8，所以3/4 就变成6/8，1/2 就变成4/8，这样式子就变成了6/8 + 7/8 - 4/8。

”同学们一听，眼睛都亮了，纷纷点头，这不就简单多啦？然后老师又出了一道题：“5/6 × 4/7 + 5/6 × 3/7”。

这可又把大家难住了，这该咋算呢？有个同学小声说：“难道要一个一个乘完再加起来？”老师摇摇头说：“不用那么麻烦，同学们看看，这里有个相同的因数5/6，这不就像咱们分糖果，有一堆一样的糖果可以先拿出来嘛！咱们可以用乘法分配律，把5/6 提出来，式子就变成5/6 × （4/7 + 3/7）。

”大家一听，哇，原来是这样啊！还有一次，老师出了这样一道题：“2/9 ÷ 5/6 × 3/5”。

有个同学马上就开始从左往右算，算着算着就乱了。

老师笑着说：“咱们可以把除法变成乘法，除以一个数等于乘以它的倒数，这样式子就变成2/9 × 6/5 × 3/5。

”然后再约分，一下子就得出答案啦！这就好像在走迷宫，找到了正确的路，一下子就走出去了！在学习分数简便计算的过程中，我们小组也经常一起讨论。

有一次，我和同桌小明还有后面的小红一起做一道题，“1 - 1/2 - 1/4 - 1/8 - 1/16”。

人教版五年级下册分数简便计算
1. 简便计算百分数：
- 如果要计算一个数的百分之几，可以将这个数除以100，并将小数点右移两位。

- 例如，计算80的百分之20：80 ÷ 100 × 20 = 0.8 × 20 = 16。

2. 简便计算比例：
- 如果要计算一个数的比例，例如5比12，可以将这个数除以12，然后再乘以5。

- 例如，计算5比12的数：12 ÷ 12 × 5 = 5。

3. 简便计算加减：
- 如果两个数相加或相减时其中一个数是整百、整千、整万等形式，可以将该数视作0并直接计算。

- 例如，计算63 + 100：63 + 100 = 63 + 00 = 63。

4. 简便计算乘除：
- 如果一个数乘以一个整百、整千、整万等形式的数，可以将这两个数相乘后直接去掉相应位数的零。

- 例如，计算32 × 100：32 × 100 = 3200 = 320。

注意：以上方法只适用于相对较简单的计算，对于复杂的计算仍然需要使用正常的算术运算。