卫星坐标计算

第三章GPS 卫星的坐标计算在用GPS 信号进行导航定位以及制订观测计划时，都必须已知GPS 卫星在空间的瞬间位置。

卫星位置的计算是根据卫星导航电文所提供的轨道参数按一定的公式计算的。

3.1卫星运动的轨道参数3.1.1基本概念 1.作用在卫星上力卫星受的作用力主要有：地球对卫星的引力，太阳、月亮对卫星的引力，大气阻力，大气光压，地球潮汐力等。

中心力：假设地球为匀质球体的引力（质量集中于球体的中心），即地球的中心引力，它决定卫星运动的基本规律和特征，决定卫星轨道，是分析卫星实际轨道的基础。

此种理想状态时卫星的运动称为无摄运动，卫星的轨道称为无摄轨道。

摄动力：也称非中心力，包括地球非球形对称的作用力、日月引力、大气阻力、大气光压、地球潮汐力等。

摄动力使卫星运动产生一些小的附加变化而偏离理想轨道，同时这种偏离量的大小随时间而改变。

此种状态时卫星的运动称为受摄运动，卫星的轨道称为受摄轨道。

虽然作用在卫星上的力很多，但这些力的大小却相差很悬殊。

如果将地球引力当作1的话，其它作用力均小于10-5。

2.二体问题研究两个质点在万有引力作用下的运动规律问题称为二体问题。

3．卫星轨道和卫星轨道参数卫星在空间运行的轨迹称为卫星轨道。

描述卫星轨道状态和位置的参数称为轨道参数。

3.1.2卫星运动的开普勒定律 （1）开普勒第一定律卫星运行的轨道为一椭圆，该椭圆的一个焦点与地球质心重合。

此定律阐明了卫星运行轨道的基本形态及其与地心的关系。

由万有引力定律可得卫星绕地球质心运动的轨道方程。

r 为卫星的地心距离，as 为开普勒椭圆的长半径，es 为开普勒椭圆的偏心率；fs 为真近点角，它描述了任意时刻卫星在轨道上相对近地点的位置，是时间的函数。

（2）开普勒第二定律卫星的地心向径在单位时间内所扫过的面积相等。

表明卫星在椭圆轨道上的运行速度是不断变化的，在近地点处速度最大，在远地点处速度最小。

近地点远地点ss s s f e e a r cos 1)1(2+-=（3卫星运行周期的平方与轨道椭圆长半径的立方之比为一常量，等于GM 的倒数。

卫星定位公式【原创版】目录1.卫星定位的基本原理2.卫星定位公式的构成3.卫星定位公式的应用4.卫星定位技术的发展正文1.卫星定位的基本原理卫星定位系统是一种利用卫星发射的信号来确定地球表面某一点的精确位置的技术。

其基本原理可以概括为：测量卫星发射的信号从卫星到达地面某一点的时间，根据光速和时间的关系，计算出该点与卫星之间的距离。

同时，通过至少三个卫星的定位，可以确定该点的三维坐标。

2.卫星定位公式的构成卫星定位公式主要包括以下三个部分：(1) 计算卫星与地面点之间的距离公式：d = c * t，其中 d 为距离，c 为光速（约为 3 * 10^8 米/秒），t 为信号传输时间。

(2) 计算卫星的轨道参数公式：T = 2 * π * sqrt(a^3 / μ)，其中 T 为卫星的周期，a 为卫星的半长轴，μ为地球的标准引力参数。

(3) 计算地面点的三维坐标公式：x = (t1 * cos(E1) - t2 * cos(E2)) * cos(A) + (t1 * sin(E1) - t2 * sin(E2)) * sin(A)，y = (t1 * cos(E1) - t2 * cos(E2)) * sin(A) - (t1 * sin(E1) - t2 * sin(E2)) * cos(A)，z = (t1 * cos(E1) + t2 * cos(E2)) * cos(I) + (t1 * sin(E1) + t2 * sin(E2)) * sin(I)，其中 x、y、z 为地面点的三维坐标，t1、t2 为卫星 1、卫星 2 的信号传输时间，E1、E2、I 分别为卫星 1、卫星 2 的倾角和地球的倾角。

3.卫星定位公式的应用卫星定位公式广泛应用于各种定位导航系统，如我国的北斗卫星导航系统、美国的 GPS 系统等。

这些系统通过卫星发射的信号，实时计算接收器与卫星之间的距离，从而实现对地球表面的精确定位。

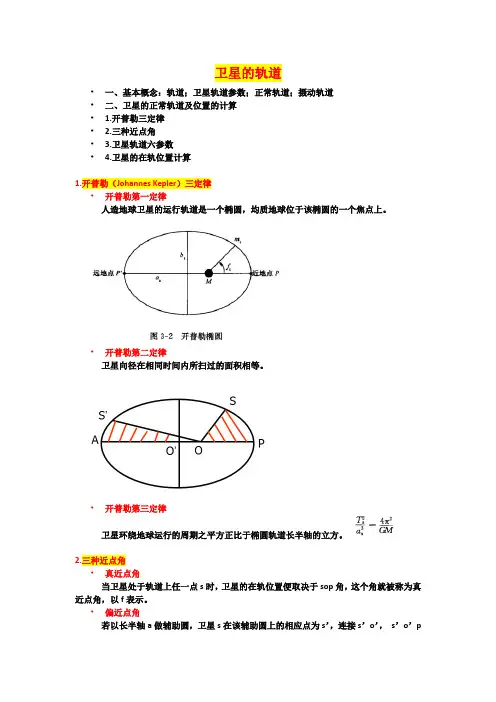
卫星的轨道•一、基本概念：轨道；卫星轨道参数；正常轨道；摄动轨道•二、卫星的正常轨道及位置的计算• 1.开普勒三定律• 2.三种近点角• 3.卫星轨道六参数• 4.卫星的在轨位置计算1.开普勒（Johannes Kepler）三定律•开普勒第一定律人造地球卫星的运行轨道是一个椭圆，均质地球位于该椭圆的一个焦点上。

•开普勒第二定律卫星向径在相同时间内所扫过的面积相等。

•开普勒第三定律卫星环绕地球运行的周期之平方正比于椭圆轨道长半轴的立方。

2.三种近点角•真近点角当卫星处于轨道上任一点s时，卫星的在轨位置便取决于sop角，这个角就被称为真近点角，以f表示。

•偏近点角若以长半轴a做辅助圆，卫星s在该辅助圆上的相应点为s’，连接s’o’，s’o’p角称为偏近点角，以E表示。

•平近点角在轨卫星从过近地点时元t p开始，按平均角速度n0运行到时元t的弧，称为平近点角。

3.卫星轨道六参数•长半轴（a）—— 卫星椭圆轨道的长半轴；•偏心率（e）—— 卫星椭圆轨道的偏心率，是焦距的一半与长半轴的比值；•真近点角（f）——在椭圆轨道上运行的卫星S，其卫星向径OS与以焦点O指向近地点P的极轴OP的夹角。

•轨道平面倾角（i）—— 卫星轨道平面与天球赤道平面的夹角；•升交点赤经（Ω）—— 升交点（N），是由南向北飞行的卫星，其轨道与天球赤道的交点。

地球环绕太阳公转的一圈中有一个点（即日历上表示的春分时间），它反映在天球赤道平面上的固定位置，叫做春分点。

升交点赤经是春分点轴向东度量到升交点的弧度；•近地点角距（ω）—— 是由升交点轴顺着卫星运行方向度量到近地点的弧长.4.卫星的在轨位置计算•在卫星导航应用中，一般根据已知的6 个轨道参数求出卫星的在轨实时位置。

•对于任意观测时刻t,•---> n ---> E ---> f•计算卫星在轨道直角坐标系中的位置卫星的摄动轨道• 1.摄动轨道• 2.摄动方程• 3.摄动结果a-b=21.3km1.导航卫星的摄动力•地心引力f0•地球非中心引力fg•地球潮汐摄动力ft•太阳引力fs•月球引力fm•大气阻力fd•太阳辐射压力fr•太阳反照压力fa2.摄动轨道概念：卫星在宇宙空间运行时由于受到地心引力之外的其他各种力的作用，如地球非中心引力，日月引力，太阳辐射压力，大气阻力及潮汐力等的合成作用，使得卫星的实际运行轨道比正常轨道复杂得多，这种实际轨道就叫做摄动轨道。

C语言计算星历位置GPS广播星历计算卫星位置和速度C语言是一种通用的高级编程语言，可以用于计算星历位置以及计算GPS卫星位置和速度。

下面将详细介绍如何使用C语言来实现这些计算。

首先，我们需要了解星历和GPS广播星历的概念。

星历是一种描述天体位置的方法，它包含了每个天体的位置坐标、速度以及其他相关的信息。

星历常用于天文学研究和导航系统中。

GPS广播星历是由GPS卫星广播的星历信息，它包含了GPS卫星所处的位置、速度等信息。

通过接收并解码广播星历，我们可以计算出卫星的位置和速度。

在C语言中，我们可以使用数学库和一些公式来计算星历位置和GPS 卫星位置以及速度。

首先，我们需要导入数学库，可以使用`#include <math.h>`导入。

数学库提供了一些常用的数学函数，如计算平方根、计算三角函数等。

然后，我们需要根据星历或广播星历的信息，计算出卫星的位置和速度。

对于星历位置的计算，可以使用开普勒方程来逼近天体的真实位置。

开普勒方程的计算公式如下：E - e * sin(E) = M其中，E为偏近点角，e为偏心率，M为平近点角。

通过迭代计算，可以得到E的近似值。

然后，利用半长轴、偏心率和E的值，可以计算出卫星在轨道平面上的坐标。

对于GPS卫星位置和速度的计算，可以使用广播星历中的卫星钟差、偏心率修正项等信息。

具体的计算公式较为复杂，需要使用专门的算法进行计算。

在计算过程中，我们还需要考虑坐标系的转换，以确保最终计算得到的是相对于地球的地心坐标系中的位置和速度。

最后，我们可以将计算得到的卫星位置和速度输出，以便进行后续的处理或导航操作。

总结来说，使用C语言计算星历位置和GPS卫星位置和速度需要导入数学库并使用开普勒方程以及其他相关的计算公式来进行计算。

同时，还需要考虑坐标系的转换和其他相关的因素。

这只是一个简单的介绍，具体的实现可能需要更多的代码和算法。

GPS坐标的表示方法GPS(Global Positioning System)是一种通过卫星定位系统来确定地理位置的技术。

在GPS中，坐标是表示位置的关键要素。

本文将介绍GPS坐标的表示方法。

1. 经纬度表示法经纬度是最常用的GPS坐标表示方法之一。

地球可以被看作是一个球体，因此需要使用一个三维坐标系来确定一个地理位置。

经度表示位置的东西方向，而纬度表示位置的南北方向。

1.1 度分秒表示法度分秒(Degrees Minutes Seconds, DMS)是经纬度表示中最常见的一种方式。

它将经度和纬度表示为度、分和秒的组合。

例如，一个地点的经度为114度4分23秒，纬度为30度12分56秒，可以表示为：114°4’23’‘E，30°12’56’’N。

1.2 十进制度表示法十进制度(Decimal Degrees, DD)是另一种流行的经纬度表示法。

它简化了坐标的表示，将度、分和秒合并为一个小数。

例如，上述地点的经度为114.0730556度，纬度为30.2155556度。

在十进制度表示法下，可以表示为：114.0730556°E，30.2155556°N。

2. 坐标系表示法除了经纬度表示法外，GPS坐标还可以用坐标系表示。

坐标系是一个平面定义的二维坐标系统，可以用数学方式来计算位置。

2.1 WGS84坐标系WGS84(World Geodetic System 1984)坐标系是GPS系统默认使用的坐标系。

它由一组数学模型和测量数据所构成，用于在三维球体上进行位置的计算。

WGS84坐标系是国际标准，广泛用于航空、测量和导航等领域。

2.2 UTM坐标系UTM(Universal Transverse Mercator)坐标系是一种广泛应用于地理测量和地图绘制的坐标系统。

它将地球表面划分为60个纵向带和20个横向带，每个带都采用横轴为东西方向和纵轴为南北方向的笛卡尔坐标系。

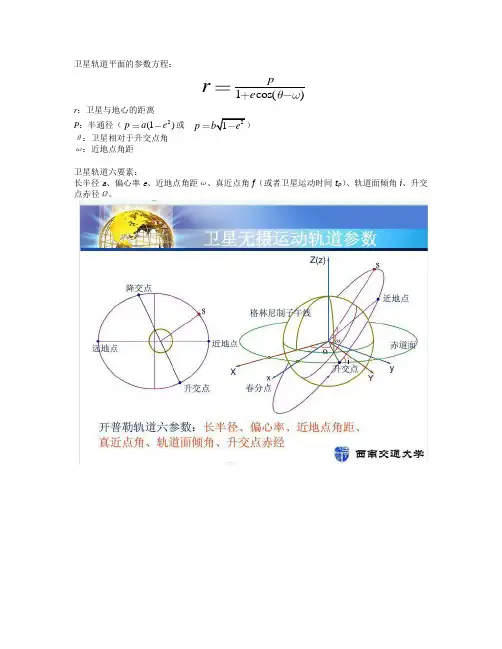
卫星轨道平面的参数方程：1cos()p e rr ：卫星与地心的距离P ：半通径（2(1)p a e 或21p b e ） θ：卫星相对于升交点角 ω：近地点角距卫星轨道六要素：长半径a 、偏心率e 、近地点角距ω、真近点角f （或者卫星运动时间t p ）、轨道面倾角i 、升交点赤径Ω。

OXYZ─赤道惯性坐标系，X轴指向春分点T ；ON─卫星轨道的节线（即轨道平面与赤道平面的交线），N为升交点；S─卫星的位置；P─卫星轨道的近地点；f─真近点角，卫星位置相对于近地点的角距；ω─近地点幅角，近地点到升交点的角距；i─轨道倾角，卫星通过升交点时，相对于赤道平面的速度方向；Ω─升交点赤经，节线ON与X轴的夹角；e─偏心率矢量，从地心指向近地点，长度等于e；W─轨道平面法线的单位矢量，沿卫星运动方向按右旋定义，它与Z轴的夹角为i；a─半长轴；α，δ─卫星在赤道惯性坐标系的赤经、赤纬。

两个坐标系：地心轨道坐标系、赤道惯性坐标系。

地心轨道坐标系Ox0y0z0：以ee1为x0轴的单位矢量，以W为z0轴的单位矢量，y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定，它位于轨道平面内。

赤道惯性坐标系：OXYZ,X轴指向春分点。

由地心轨道坐标系到赤道惯性坐标系的转换：1.先将地心轨道坐标绕W旋转角（-ω），旋转矩阵为R Z(-ω)；2.绕节线ON旋转角（-i），旋转矩阵为R X(-i)；3.最后绕Z轴旋转角（-Ω），旋转矩阵为R Z(-Ω)；经过三次旋转后，地心轨道坐标系和赤道惯性坐标系重合。

在地心轨道坐标系中，卫星的位置坐标是：0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是：000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后，可与r 、α、δ联系起来，关系式如下：1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知，则可以解出α、δ。

java 卫星覆盖地面坐标计算摘要：1.卫星覆盖地面坐标计算的概述2.Java编程语言介绍3.卫星覆盖地面坐标计算的算法实现4.代码示例与解析5.算法优化与拓展正文：随着我国航天事业的飞速发展，卫星技术在通信、导航、遥感等领域发挥着越来越重要的作用。

卫星覆盖地面坐标的计算成为卫星应用中的关键环节。

本文将介绍如何使用Java编程语言实现卫星覆盖地面坐标的计算，并提供一个代码示例。

一、卫星覆盖地面坐标计算的概述卫星覆盖地面坐标计算主要是根据卫星的轨道参数和地球的物理参数，确定卫星在某一时段内覆盖的地球表面区域。

覆盖区域的边界线是由卫星轨道的立体角和地球表面的高度决定的。

立体角可以通过卫星轨道参数和地球半径计算得出。

二、Java编程语言介绍Java是一种面向对象的编程语言，具有跨平台、高效、安全等特点。

Java 语言广泛应用于企业级应用、移动应用、Web开发等领域。

在本篇中，我们将使用Java实现卫星覆盖地面坐标的计算。

三、卫星覆盖地面坐标计算的算法实现1.计算卫星轨道的立体角卫星轨道的立体角可以通过卫星的轨道参数（包括轨道半长轴、轨道倾角、升交点赤经等）和地球半径计算得出。

计算公式如下：立体角= 2 * arcsin(r / (r + h))其中，r为卫星轨道半长轴，h为卫星轨道高度。

2.计算卫星覆盖区域的四至经纬度根据卫星轨道的立体角和地球半径，可以计算出卫星在某一时段内覆盖的地球表面区域的四个顶点的经纬度。

计算公式如下：θ= arcsin(r / (r + h))φ= arctan(√(1 - (r / (r + h))^2) / ((r + h) / 2))λ1、λ2 = θ + Δλ其中，Δλ为卫星轨道横截面上卫星投影的间隔。

java 卫星覆盖地面坐标计算摘要：1.引言2.Java 卫星覆盖地面坐标计算的原理3.Java 卫星覆盖地面坐标计算的方法4.Java 卫星覆盖地面坐标计算的实例5.总结正文：卫星覆盖地面坐标的计算在GPS 定位、航空航天、军事等多个领域有着广泛的应用。

在Java 编程语言中，我们可以通过一些数学计算和坐标转换的方法来实现卫星覆盖地面坐标的计算。

本文将详细介绍Java 卫星覆盖地面坐标计算的原理、方法和实例。

一、Java 卫星覆盖地面坐标计算的原理Java 卫星覆盖地面坐标计算的原理主要基于球面三角学和椭圆几何学。

在球面三角学中，我们通常使用球面角度和球面距离来描述地球表面的点之间的位置关系。

而在椭圆几何学中，我们使用椭球面和地球长半轴、扁平半轴等参数来描述地球表面的形状。

通过这两种数学模型，我们可以推导出卫星覆盖地面坐标计算的基本公式。

二、Java 卫星覆盖地面坐标计算的方法在Java 中，我们可以通过以下步骤实现卫星覆盖地面坐标计算：1.建立地球椭球模型：根据地球的形状参数，建立一个地球椭球模型。

2.计算卫星轨道参数：根据卫星的轨道参数（如倾角、升交点赤经、轨道半径等），计算卫星在地球椭球上的位置。

3.计算地面坐标：根据卫星的轨道参数和地球椭球模型，计算地面坐标的经度和纬度。

4.将地面坐标转换为地理坐标：根据经纬度和地球长半轴、扁平半轴等参数，将地面坐标转换为地理坐标（即地球表面上的真实坐标）。

三、Java 卫星覆盖地面坐标计算的实例下面，我们通过一个具体的Java 实例来演示卫星覆盖地面坐标计算的过程：```javaimport java.util.Scanner;public class SatelliteCoordinateCalculation {public static void main(String[] args) {// 输入卫星轨道参数double inclination = 5.0; // 倾角（单位：度）double ra = 120.0; // 升交点赤经（单位：度）double r = 6000.0; // 轨道半径（单位：公里）// 计算地面坐标double longitude = calculateLongitude(inclination, ra, r);double latitude = calculateLatitude(inclination, ra, r);// 输出结果System.out.println("地面坐标：经度：" + longitude + "°，纬度：" + latitude + "°");}// 计算经度public static double calculateLongitude(double inclination, double ra, double r) {// 公式实现}// 计算纬度public static double calculateLatitude(double inclination, double ra, double r) {// 公式实现}}```通过以上实例，我们可以看到Java 卫星覆盖地面坐标计算的过程。

GPS卫星的坐标计算第三章GPS 卫星的坐标计算在⽤GPS 信号进⾏导航定位以及制订观测计划时，都必须已知GPS 卫星在空间的瞬间位置。

卫星位置的计算是根据卫星导航电⽂所提供的轨道参数按⼀定的公式计算的。

3.1卫星运动的轨道参数3.1.1基本概念 1.作⽤在卫星上⼒卫星受的作⽤⼒主要有：地球对卫星的引⼒，太阳、⽉亮对卫星的引⼒，⼤⽓阻⼒，⼤⽓光压，地球潮汐⼒等。

中⼼⼒：假设地球为匀质球体的引⼒（质量集中于球体的中⼼），即地球的中⼼引⼒，它决定卫星运动的基本规律和特征，决定卫星轨道，是分析卫星实际轨道的基础。

此种理想状态时卫星的运动称为⽆摄运动，卫星的轨道称为⽆摄轨道。

摄动⼒：也称⾮中⼼⼒，包括地球⾮球形对称的作⽤⼒、⽇⽉引⼒、⼤⽓阻⼒、⼤⽓光压、地球潮汐⼒等。

摄动⼒使卫星运动产⽣⼀些⼩的附加变化⽽偏离理想轨道，同时这种偏离量的⼤⼩随时间⽽改变。

此种状态时卫星的运动称为受摄运动，卫星的轨道称为受摄轨道。

虽然作⽤在卫星上的⼒很多，但这些⼒的⼤⼩却相差很悬殊。

如果将地球引⼒当作1的话，其它作⽤⼒均⼩于10-5。

2.⼆体问题研究两个质点在万有引⼒作⽤下的运动规律问题称为⼆体问题。

3．卫星轨道和卫星轨道参数卫星在空间运⾏的轨迹称为卫星轨道。

描述卫星轨道状态和位置的参数称为轨道参数。

3.1.2卫星运动的开普勒定律（1）开普勒第⼀定律卫星运⾏的轨道为⼀椭圆，该椭圆的⼀个焦点与地球质⼼重合。

此定律阐明了卫星运⾏轨道的基本形态及其与地⼼的关系。

由万有引⼒定律可得卫星绕地球质⼼运动的轨道⽅程。

r 为卫星的地⼼距离，as 为开普勒椭圆的长半径，es 为开普勒椭圆的偏⼼率；fs 为真近点⾓，它描述了任意时刻卫星在轨道上相对近地点的位置，是时间的函数。

（2）开普勒第⼆定律卫星的地⼼向径在单位时间内所扫过的⾯积相等。

表明卫星在椭圆轨道上的运⾏速度是不断变化的，在近地点处速度最⼤，在远地点处速度最⼩。

近地点远地点ss s s f e e a r cos 1)1(2+-=（3卫星运⾏周期的平⽅与轨道椭圆长半径的⽴⽅之⽐为⼀常量，等于GM 的倒数。

《卫星导航定位算法与程序设计》课程常用参数和常用公式一览编制人：刘晖更新时间：2010年10月29日1、常用参考框架的几何和物理参数1.1 ITRFyy 主要的大地测量常数长半轴a=6.3781366×106m；地球引力常数（含大气层）GM=3.986004418×1014 m3/s2；地球动力因子J2=1.0826359×10-3；地球自转角速度ω=7.292115×10-5 rad/s。

扁率1/f =298.25642；椭球正常重力位U0=6.26368560×107 m2/s2；γ=9.7803278 m/s2；赤道正常重力e光速c=2.99792458×108 m/s。

1.2 GTRF主要的大地测量常数长半轴a=6.37813655×106 m；地球引力常数GM=3.986004415×1014 m3/s2；地球动力因子J2=1.0826267×10-3；扁率1/f =298.25769。

1.3 WGS84（Gwwww）主要的大地测量常数长半轴a=6.3781370×106 m；地球引力常数（含大气层）GM=3.986004418×1014 m3/s2；地球自转角速度ω=7.292115×10-5 rad/s。

扁率1/f =298.257223563；椭球正常重力位U0=62636860.8497 m2/s2；γ=9.7803267714m/s2；赤道正常重力e短半轴b=6356752.3142m；引力位二阶谐系数2,0C=-484.16685×10-6；第一偏心率平方2e=0.00669437999013；e'=0.006739496742227。

第二偏心率平方21.4 PZ90 主要的大地测量常数长半轴a=6.378136×106m；地球引力常数GM=3.9860044×1014 m3/s2；fM=3.5×108 m3/s2；地球大气引力常数a地球自转角速度ω=7.292115×10-5 rad/s。

经纬度计算坐标
在地理信息系统（GIS）中，经纬度是一种常见的坐标系统，用于描述地球上
的位置。

经度（Longitude）是指地球表面上一个点与地球西侧辅助子午线（Greenwich Meridian）之间的角度，而纬度（Latitude）则是指一个点与地球赤
道之间的角度。

经纬度坐标的单位是度（°），可以用来精确表示一个地点在地球
表面的位置。

经纬度的表示
经纬度用一个由两个数字组成的坐标对来表示，分别表示纬度和经度。

例如，
北京市的坐标为纬度39.9°N，经度116.4°E，可以用（39.9, 116.4）来表示。

其中，纬度的范围为-90°（南纬90°）到90°（北纬90°），经度的范围为-180°（西经180°）到180°（东经180°）。

经纬度的计算方法
在计算机程序中，经纬度的计算通常使用数学公式来实现。

以下是常用的几种
计算方法：
1. 度分秒转换为度
当经纬度使用度、分、秒来表示时，通常需要将其转换为度的形式。

转换方法
如下：
度 = 度 + 分/60 + 秒/3600
例如，将纬度39°30’40。

卫星的两行根数（Two-Line Elements，简称TLE）是描述地球轨道上的人造卫星轨道参数的一种标准数据格式。

通过这两行根数，我们可以计算卫星在任何给定时间的位置和速度。

以下是两行根数的一般格式和内容：第一行：卫星编号分类（例如，未分类、有效载荷、碎片等）国际地球观测卫星组织（International Designator）编号年份的前两位数字发射编号发射片段编号第二行：轨道倾角（i，度）升交点赤经（Ω，度）近地点幅角（ω，度）平均运动（n，度/天）革命次数在Epoch时刻后（M，度）近地点距离（e，地球半径）为了从TLE计算卫星的位置和速度，我们通常使用SGP4（Simplified General Perturbations 4）算法。

SGP4是一个广泛使用的算法，用于根据TLE预测卫星的位置和速度。

SGP4算法相当复杂，涉及多个步骤和子计算。

在这里简要概述其主要步骤：初始化：使用TLE中的参数初始化卫星的轨道元素。

计算平均元素：通过平均运动n计算平均角速度，从而得到平均近点角M0。

考虑摄动：考虑地球引力、日月引力、大气阻力等摄动因素对卫星轨道的影响。

计算真近点角：通过平均近点角M0和摄动计算真近点角M。

计算位置和速度：使用真近点角M和其他轨道元素计算卫星在ECEF坐标系中的位置和速度。

输出：将计算结果转换为所需的坐标系统（如地理坐标）。

需要注意的是，SGP4是一个相当复杂的算法，通常需要使用专门的软件库来实现。

如果需要进行详细的卫星轨道计算或模拟，建议使用现有的SGP4库或软件工具，而不是从头开始编写算法。

gnss观测方程
GNSS（全球导航卫星系统）观测方程是一组用于计算定位和测量卫星位置的数学方程。

这些方程是基于测量接收器接收到的卫星信号的时间延迟来确定接收器的位置。

下面我将以人类的视角来描述这些方程的原理和应用。

GNSS观测方程是通过测量接收器接收到的卫星信号的时间差来计算接收器位置的数学方程。

这些卫星信号通过卫星定位系统发送，接收器接收到信号后，测量信号传播的时间差，进而计算出接收器与卫星之间的距离。

GNSS观测方程的计算原理是基于测量信号传播时间差的三角定位原理。

接收器接收到多个卫星的信号后，根据信号传播时间与信号传播速度的关系，可以计算出接收器与每个卫星之间的距离。

通过多个卫星的距离测量，可以得到接收器的三维位置坐标。

GNSS观测方程在定位和导航应用中具有广泛的应用。

例如，在航空航天领域，GNSS观测方程被用于飞行导航和飞行器定位。

在地理信息系统中，GNSS观测方程被用于地图制作和位置服务。

此外，GNSS观测方程还被用于军事应用、海洋测量和环境监测等领域。

GNSS观测方程的精度和可靠性取决于多个因素，包括卫星的准确位置、接收器的精度和环境条件等。

为了提高定位的精度和可靠性，GNSS观测方程通常与其他辅助信息一起使用，例如地面测量数据和
地图数据。

GNSS观测方程是一组用于计算定位和测量卫星位置的数学方程。

通过测量接收器接收到的卫星信号的时间差，可以计算出接收器与卫星之间的距离，从而实现定位和导航功能。

这些方程在航空航天、地理信息系统和其他领域具有广泛的应用，为人类的生活和工作提供了便利和准确性。