高二下理科数学：选修2—3周周清(第5周)

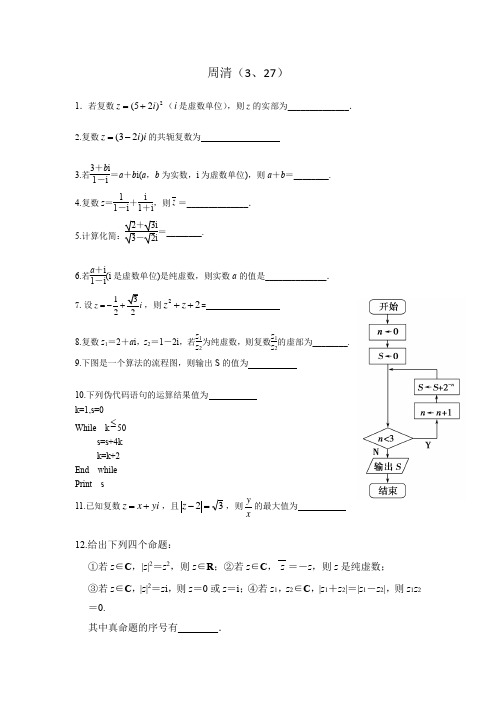
周清（3、27）1．若复数2)25(i z +=（i 是虚数单位），则z 的实部为______________．2.复数i i z )23(-=的共轭复数为3.若3＋b i 1－i＝a ＋b i(a ，b 为实数，i 为虚数单位)，则a ＋b ＝________. 4.复数z ＝11－i ＋i 1＋i，则z ＝______________． 5.计算化简：2＋3i3－2i ＝________.6.若a ＋i 1－i(i 是虚数单位)是纯虚数，则实数a 的值是______________． 7.设132z i =-+，则22++z z =8.复数z 1＝2＋a i ，z 2＝1－2i ，若z 1z 2为纯虚数，则复数z 1z 2的虚部为________. 9.下图是一个算法的流程图，则输出S 的值为10.下列伪代码语句的运算结果值为k=1,s=0While k ≤50s=s+4kk=k+2End whilePrint s11.已知复数yi x z +=，且32=-z ，则xy 的最大值为 12.给出下列四个命题：①若z ∈C ，|z |2＝z 2，则z ∈R ；②若z ∈C ，z ＝－z ，则z 是纯虚数； ③若z ∈C ，|z |2＝z i ，则z ＝0或z ＝i ；④若z 1，z 2∈C ，|z 1＋z 2|＝|z 1－z 2|，则z 1z 2＝0.其中真命题的序号有________．13.计算：(1)(－1＋i )(2＋i )i 3； (2)1－3i (3＋i )2； (3)1＋i (1－i )2＋1－i (1＋i )2.14.已知z 是复数，z ＋2i 、z 2－i均为实数(i 为虚数单位)，且复数(z ＋a i)2在复平面内对应的点在第一象限，求实数a 的取值范围.15.设z 是虚数，已知ω＝z ＋1z 是实数，且－1<ω<2.(1)求|z |的值及z 的实部的取值范围；(2)设u ＝1－z 1＋z，求证：u 为纯虚数； (3)求ω－u 2的最小值．清明假期作业1、不等式3x 2－x －4≤0的解集是__________.2、不等式1－2x x ＋1>0的解集是________．3、不等式x 2>x 的解集是________ .4、不等式x>1x的解集为 ________.5、不等式)9x 2－6x ＋1≥0解集为 ________.6、函数y ＝log 12(x 2－1)的定义域是____________．7、不等式x ＋1x<3的解集是________．8、不等式3＋2x －x 2≥0的解集是________．9、不等式－x 2＋2x ＜3的解集是________．10、不等式1＋x －x 3－x 4＜0的解集是________．12、不等式－1≤x2＋2x－1≤2的解集是________．13、已知不等式x2－2x＋k2－3>0对一切实数x恒成立，则实数k的取值范围是________．14、已知函数f(x)＝x2＋ax＋3.(1)当x∈R时，f(x)≥a恒成立，求a的取值范围；(2)当x∈[－2,2]时，f(x)≥a恒成立，求a的取值范围．周周清（4、10）1、若2,4,2x ,4y 四个数的平均数是5，则=+y x2、计算：=+-i i 1252 ；（期中i 为虚数单位） 3、若复数z 满足：i i z +=+1)32(，则z = ；4、阅读右边的程序框图，运行相应的程序，若输入x 的值为－4，则输出y 的值为________．5、下列伪代码语句的运算结果值为k=1,s=0While k ≤10s=s+k2k=k+1End whilePrint s6、在100张奖券中，有4张中奖，从中任取一张，中奖的概率是 ．7、从2,3,8,9中任取两个不同的数字，分别记为b a ,,则b a log 为整数的概率为8、投掷两颗骰子，得到其向上的点数分别为m,n ，则复数))((mi n ni m -+为实数的概率为9、连续两次抛掷一枚六面的骰子，则事件‘两次数字之和等于7’发生的概率为10、已知数据12345,,,,x x x x x 的方差为4，则数据1234551,51,51,51,51x x x x x -----的方差为 ．11、已知函数]5,5[,2)(2-∈--=x x x x f ，若从区间[-5,5]内随机取一个数0x ，则所取0x 满足0)(0<x f 的概率为12、在ABC ∆内任取点P ，求使得ABC BPC S S ∆∆>21的的概率为13、袋中装有红、黄、白3种颜色的球各1只，每次从中任取1只，有放回地抽取3次，分别求下列事件的概率：（1）3只全是红球；（2）3只颜色全相同；（3）3只颜色不全相同；14、15、已知不等式：aaxx+>++2232；（1）若2=a，解上述不等式；（2）若对于Rx∈上述不等式恒成立，求a的取值范围；（3）若对于]1,1[-∈a上述不等式恒成立，求x的取值范围。

高二理科数学周周清练习2（满分100分，测试时间45分钟）班级 姓名 座号 成绩：一、选择题：本大题共7小题，每小题7分，共49分． 1. 已知幂函数f (x )=x α过点(,),则α等于（ ）A.3B.2C.D. 2．函数f (x )=2|x-1|的图象大致是（ ）3．若a=log 20.9,b=133-,c=121()3,则( )(A)a<b<c (B)a<c<b (C)c<a<b (D)b<c<a4．函数f(x)=23xx +的零点所在的一个区间是( )(A)（-2，-1） (B)（-1,0） (C)（0,1） (D)（1,2）5．已知函数f (x )的导函数为f ′(x )，且满足f (x )＝2xf ′(1)＋ln x ，则f ′(1)＝( )A ．－eB ．－1C ．1D ．e6．函数f (x )＝(x －3)e x的单调递增区间是( )A ．(－∞，2)B ．(0,3)C ．(1,4)D ．(2，＋∞) 7．已知函数f (x )=若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则abc 的取值范围是（ ）A .(1,10)B .(5,6)C .(10,12)D .(20,24) 二、填空题：本大题共3小题，每小题7分，共21分． 8．直线12y x b =+是曲线()ln 0y x x =>的一条切线，则实数b ＝ ． 9．若函数f (x )＝－13x 3＋12x 2＋2ax 在⎣⎢⎡⎭⎪⎫23，＋∞上存在单调递增区间，则a 的取值范围是________． 10．函数f (x )=log a x (a>0且a ≠1)在区间[a ,2a ]上的最大值与最小值之差为,则a 等于 .三、解答题：本大题共3小题，每小题10分，共30分． 11. 如果幂函数f (x )=(p ∈Z)是偶函数,且在(0,+∞)上是增函数,求p 的值,并写出相应的函数f (x )的解析式.12．如图所示，已知边长为8米的正方形钢板有一个角被锈蚀，其中AE ＝4米，CD ＝6米．为合理利用这块钢板，在五边形ABCDE 内截取一个矩形BNPM ，使点P 在边DE 上．(1)设MP ＝x 米，PN ＝y 米，将y 表示成x 的函数，求该函数的解析式及定义域； (2)求矩形BNPM 面积的最大值．13．已知函数f (x )＝ln x ＋kex(k 为常数)，曲线y ＝f (x )在点(1，f (1))处的切线与x 轴平行． (1)求k 的值；(2)求f (x )的单调区间．高二理科数学周周清练习2参考答案：选择题1—7 CBB BBD C填空题8．ln2-1； 9．⎝ ⎛⎭⎪⎫－19，＋∞；10．4或1/4 解答题11．解：∵f (x )在(0,+∞)上是增函数,∴-p 2+p+>0,即p 2-2p-3<0,∴-1<p<3. .............................................. 5分又∵f (x )是偶函数且p ∈Z, ∴p=1,故f (x )=x 2. ...................................................................... 10分12．解：(1)作PQ ⊥AF 于Q ，所以PQ ＝(8－y )米， EQ ＝(x －4)米． 又△EPQ ∽△EDF ，所以EQ PQ ＝EF FD ，即x －48－y ＝42.所以y ＝－12x ＋10，定义域为{x |4≤x ≤8}． ---------------------------5分(2)设矩形BNPM 的面积为S 平方米，则S (x )＝xy ＝x ⎝⎛⎭⎪⎫10－x 2＝－12(x －10)2＋50，S (x )是关于x 的二次函数，且其图象开口向下，对称轴为x ＝10，所以当x ∈[4,8]时，S (x )单调递增． 所以当x ＝8米时，矩形BNPM 的面积取得最大值，为48平方米．------------10分13．解：(1)由题意得f ′(x )＝1x－ln x －k ex， 又f ′(1)＝1－ke ＝0，故k ＝1. ---------------------------5分(2)由(1)知，f ′(x )＝1x－ln x －1ex. 设h (x )＝1x －ln x －1(x ＞0)，则h ′(x )＝－1x 2－1x＜0，即h (x )在(0，＋∞)上是减函数．由h (1)＝0知，当0＜x ＜1时，h (x )＞0，从而f ′(x )＞0； 当x ＞1时，h (x )＜0，从而f ′(x )＜0.综上可知，f (x )的单调递增区间是(0,1)，单调递减区间是(1，＋∞)．-----10分。

高三理科数学周周清命题人：张湖生一．选择题（每小题5分）1．已知α是第二象限角，tan(2πα+)=-43,则tan α=( ) A.2 B. -12 C . -12或2 D.-43,2，设函数f(x) =4sin(2x+1)-x,则在下列区间中函数f(x)不存在零点的是（ ） A. [-4，-2] B. [-2,0] C. [0,2] D.,[2,4] 3,函数f(x)=sinx 在区间[a,b]上是增函数，且f(a)=-1,f(b)=1，则cos2a b+=( )A.0B.2C.-1D.1 4,若函数y=2cos(2x+ϕ)是偶函数，且在(0,4π)上是增函数，则ϕ的可能值是（ ） A.2π-B.0C.2πD. π 5. 设02x π<<，则2"sin 1"x x <是"sin 1"x x <的（ ）条件A ．充分不必要 B.必要不充分C ．充分必要 D.既不充分又不必要 6. 已知0,ω>函数()sin()4f x x πω=+在(,)2ππ上单调递减，则ω的取值范围是（ ） A ．15[,]24 B.13[,]24C.1(0,]2D. (0,2]7. 已知角θ的顶点与原点重合，始边与x 轴正半轴重合，终边在直线2y x =上，则cos 2()θ=A ．45-B.35-C.35D. 458. 在ABC ∆中，3sin 4cos 6,4sin 3cos 1,A B B A +=+=则sin C 的值为（ ）A ．12 B.2 C.2 D.139. 在平面直角坐标系中，0(0,0),(6,8),P 将向量OP uuu r 按逆时针旋转34π后得到向量OQ uuu r ，则点Q 的坐标是（ ）A ．(- B.(- C. (2)-- D. (2)-OX110. 如果33sin cos 0,θθ+<那么sin cos θθ+的取值范围为（ ）A ．[2,0]- B.[2,1)- C.(0,2] D. (0,2)二．填空题（每小题5分，其中11、12、13任选两小题） 11.已知曲线C 的极坐标方程为24cos sin θρθ=，直线l 的参数方程为cos (1sin x t t y t ααπα=⎧≤⎨=+⎩为参数，0<），若直线l 经过点（1,0），则直线l 被曲线C 截得的线段AB 的长为___________ 12. 已知关于x 的不等式122x x t -++<对任意的[2,1]x ∈-恒成立，则实数t 的取值范围是___________________13. 如图，在半径为r 的圆O 中，弦AB,CD 相交于点P ，且AP=BP ，PD=02,303r OAP ∠=,则CP =_________________14. 已知函数()tan()(0,),()2f x A x y f x πωϕωϕ=+><=的部分图象如图，则f (24π)=8π 38π15.已知sin()2cos()0,(),k k k Z παπα+-+=∈则2sin cos cos sin cos ααααα++=-_________16. 满足方程222213log [2cos ()]2cos ()4xy y y xy +=-++的所有实数对(,)x y =_________答题卡： 题号 1 2 3 4 5 6 7 8 9 10 答案11. 12. 13.y14. 15. 16. 三．解答题17. 已知：1sin(3),3πθ+= 求cos()cos(2)33cos [cos()1]sin()cos()sin()22πθθππθπθθπθπθ+-+-----+的值。

重庆第二外国语学校数学周周清（第五周）重庆第二外国语学校高2021学部数学周周清（第五周）姓名：________ 班级：________ 分数：________一、选择题（本题共5小题，每题6分，共30分）1.直三棱柱ABC?A1B1C1中，若?BAC?90?，AB?AC?AA1，则异面直线BA1与AC1所成的角等于（）A.30B.45C.60D.902. 若直线l1和l2是异面直线，l1在平面?内，l2在平面?内，l是平面?与平面?的交线，则下列命题正确的是（）A．l至少与l1，l2中的一条相交 B．l与l1，l2都相交C．l至多与l1，l2中的一条相交 D．l与l1，l2都不相交 3. 某几何体的三视图如图所示,则该几何体的体积为 ( ) A.16+8π B.8 +8πC.16+16π D.8+16π4.如图:直三棱柱ABC―A1B1C1的体积为V，点P、Q分别在侧棱AA1和CC1上，AP=C1Q，则四棱锥B―APQC的体积为 A、ooooA'PB'C'VVVV B、 C、 D、 2345QABC5.已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2,则此棱锥的体积为（）A.2322B.C.D. 6632二、填空题（本题共5小题，每题6分，共30分）6.在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点,则EF与平面BB1D1D的位置关系是 .7.如图所示,直观图四边形A′B′C′D′是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是 .8.如图,P是平面ABC外一点,平面α∥平面ABC,α与线段PA,PB,PC分别交于A′,B′,C′,若PA′∶AA′=2∶3,则错误！未找到引用源。

= .9. 长方体ABCD?A1B1C1D1的顶点均在同一个球面上，AB?AA1?1，BC?则A，B两点间的球面距离为 . 三、解答题（10-11题各15分，12题16分）2，8题 O是底ABCD对角线的交点. 10、已知正方体ABCD?A1BC11D1，求证：(１) C1O∥面AB1D1；(2)面OC1D//面AB1D1．D1A1DOABB1C1C11. 如图，直三棱柱ABC-A′B′C′，∠BAC=90°，AB=AC= 2，AA′=1，点M，N分别为A′B和B′C′的中点．（Ⅰ）证明：MN∥平面A′ACC′；（Ⅱ）求三棱锥A′-MNC的体积．12. 空间四边形ABCD的对棱AD，BC成60°的角，且AD=BC=a，平行于AD与BC的截面分别交AB，AC，CD，BD于E、F、G、H．（1）求证：四边形EFGH为平行四边形；（2）E在AB的何处时截面EFGH的面积最大？最大面积是多少？感谢您的阅读，祝您生活愉快。

高二数学周周清练习题基础知识回顾（每小题2分，共14分）1. 等差数列概念：______________________________________________________2. 等差数列通项公式=a n _______________________________3.等差数列前n 项和公式=s n ____________________=__________________________4.性质：(1)若a, A,b 成等差数列，则 A=________________________(2)若q p n m +=+，则__________________________________(3) a a n m ,为数列中任意两项，则_____________________ 错题再练一. 写出下列数列的一个通项公式（每小题2分，共14分）（1）2，4 , 6 , 8 …(2) -1, 1, -1, 1…(3) 1, 2, 4, 8 ….(4)1, 4, 9, 16 …(5) 8, 88, 888, 8888 ….(6)3, 8, 15, 24 (7) (17)16,109,54,21--二 选择题（每小题5分，共30分）1.已知等差数列}{n a 满足,10,45342=+=+a a a a 则数列前10的=10S ( )A. 138B. 135C.95D.232.设数列}{n a 是单调递减的等差数列，前三项的和是12，前三项的积为48，则它的首项是（ ）A. 2B. 4 C 6. D .83.夏季高山上气温从山脚起每升高100m 降低0.5度，已知山顶的气温是14度，山脚的气温是26度，那么此山的高度（ ）A 1700B 1800C 2400D 26004.数列 (9)8,76,54,32的第10项是（ ） 2322.2120.1918.1716.D C B A 5.若数列}{n a 的前n 项的积为2n ，则当2≥n 时，数列}{n a 的通项公式为（ ）A. 12-=n a nB. 2n a n =C. 22)1(n n a n +=D. 22)1(-=n n a n 6. —401是不是数列—5，—9，—13，…的第几项？ （ ）A. 98 B 99 C 100 D 101三 计算题（共42分，1题12分，2,3,4各10分）1. 在等差数列}{n a 中，（1）已知d a S S 和求1128,168,48==（2）已知8856,5,10S a S a 和求==(3) 已知17153,20S a a 求=+2.已知}{n a 是等差数列，其中.8,311-==d a 公差（1）求数列}{n a 的通项公式（2）数列}{n a 从哪一项开始小于0？（3）求数列}{n a 前n 项和的最大值，并求出对应n 的值。

唐山一中高三数学周周清强化训练试卷（五）答案一、选择题BDDCA BDACC AC 二、填空题13、α=29π/15 14、⎥⎦⎤⎢⎣⎡+-672,62ππππk k ()Zk ∈ 15、 213a a <-≥或 16、①②⑤三、解答题17解：(1)当a ＝2时，A ＝{x |2<x <7}，B ＝{x |4<x <5}． ∴A ∩B ＝{x |4<x <5}， (2)B ＝{x |2a <x <a 2＋1}，①当B ＝Ø时，2a ≥a 2＋1，∴a ＝1， 此时A ＝{x |2<x <4}，B ⊆A 符合题意．②若B ≠Ø，方程(x －2)[x －(3a ＋1)]＝0的两根为x 1＝2，x 2＝3a ＋1. ∵B ≠Ø.∴A ≠Ø∴3a ＋1≠2，即a ≠13.当3a ＋1>2，即a >13时，⎩⎪⎨⎪⎧2a ≥2a 2＋1≤3a ＋12a <a 2＋1⇒⎩⎪⎨⎪⎧a ≥10≤a ≤3⇒1<a ≤3a ≠1.当3a ＋1<2，即a <13时，⎩⎪⎨⎪⎧2a ≥3a ＋1a 2＋1≤2⇒⎩⎪⎨⎪⎧a ≤－1－1≤a ≤1⇒a ＝－1.∴a 的取值范围为[1,3]∪{－1}．18.（1）解法一 由条件知△ABC 为直角三角形，∠BAC =90°,∵PA=PB=PC ,∴点P 在平面ABC 上的射影是△ABC 的外心，即斜边BC 的中点E ，取AC 中点D ，连结PD 、DE 、PE ，PE ⊥平面ABC .DE ⊥AC (∵DE ∥AB ).∴AC ⊥PD ,∠PDE 为二面角P-AC-B 的平面角.tan PDE =32323==aaDEPE ,∴∠PDE =60°,故二面角P-AC-B 的平面角为60°.解法二 设O 为BC 的中点，则可证明PO ⊥面ABC ，建立如图空间直角坐标系，则A ⎪⎪⎭⎫⎝⎛-0,23,21a a ,B (-a ,0,0),C (a ,0,0),P ⎪⎭⎫⎝⎛a 23,0, AC 中点D ⎪⎪⎭⎫⎝⎛-0,43,43a a , AB=⎪⎪⎭⎫⎝⎛-0,23,23a a ,DP=⎪⎪⎭⎫⎝⎛-a a a 23,43,43 ∵AB ⊥AC ,PA =PC ,PD ⊥AC ,cos<AB ,DP >即为二面角P-AC -B 的余弦值.而cos<AB ,DP >=21491631690434904323)43)(23(22222=++⨯+++⨯+--aaaaaa a a a二面角P-AC-B 的平面角为60° (2)解法一 PD =aaaDEPE349432222=+=+,S △APC =21·AC ·PD =223a设点B 到平面PAC 的距离为h , 则由V P-ABC =V B-APC 得31·S △ABC ·PE =31·S △APC ·h ,h =aaa a a S PE S APCABC 2323233212=⋅⋅⋅=⋅∆∆.故点B 到平面PAC 的距离为a23.解法二 点E 到平面PAC 的距离容易求得，为43a ,而点B 到平面PAC 的距离是其2倍,∴点B 到平面PAC 的距离为a23.19、(1)函数f (x )为奇函数，则f (－x )＝－f (x )，函数f (x )的图象关于x ＝1对称，则f (2＋x )＝f (－x )＝－f (x )，所以f (4＋x )＝f [(2＋x )＋2]＝－f (2＋x )＝f (x )，所以f (x )是以4为周期的周期函数．(2) 当x ∈[1,2]时，2－x ∈[0,1]，又f (x )的图象关于x ＝1对称，则f (x )＝f (2－x )＝22－x －1，x ∈[1,2]． (3)∵f (0)＝0，f (1)＝1，f (2)＝0，f (3)＝f (－1)＝－f (1)＝－1 又f (x )是以4为周期的周期函数．∴f (0)＋f (1)＋f (2)＋…＋f (2013)＝f (2 012)＋f (2 013)＝f (0)＋f (1)＝1. 20．（本小题满分12分）解：（1）证明：连接AO ，在1AO A 中，作1O E AA ⊥于点E ，因为11//AA BB ，得1OE B B ⊥,因为1A O ⊥平面ABC ，所以1A O BC ⊥,因为AB =得A O B C ⊥,所以B C ⊥平面1AA O ,所以BC O E ⊥所以O E ⊥平面11BB C C , 又11,AO AA ===得215AOAE AA ==(2)如图所示，分别以1,,O A O B O A 所在的直线为x,y,z 轴建立空间直角坐标系，则A(1,0,0), C(0,-2,0), A 1(0.0,2),B(0,2,0)由（1）可知115A E A A = 得点E 的坐标为42(,0,)55，由（1）可知平面11BB C C 的法向量是42(,0,)55，设平面11A B C 的法向量(,,)n x y z = ，C 1x由100n AB n A C ⎧⨯=⎪⎨⨯=⎪⎩ ，得200x y y z -+=⎧⎨+=⎩，令1y =，得2,1x z ==-，即(2,1,1)n =-所以cos ,10||||O E n O E n O E n ⨯<>==⨯即平面平面11A B C 与平面BB 1C 1C10。

高一上：必修一、二高一下：必修三、四高二上：必修五、选修1－1文、选修2－1理高二下：文选修1－2,理选修2－2、2－3高一数学上数学1第1章集合1.1集合的含义及其表示1.2子集、全集、补集1.3交集、并集第2章函数概念与基本初等函数Ⅰ2.1函数的概念和图象函数的概念和图象函数的表示方法函数的简单性质映射的概念2.2指数函数分数指数幂指数函数2.3对数函数对数对数函数2.4幂函数2.5函数与方程二次函数与一元二次方程用二分法求方程的近似解2.6函数模型及其应用数学2第3章立体几何初步3.1空间几何体棱柱、棱锥和棱台圆柱、圆锥、圆台和球中心投影和平行投影直观图画法空间图形的展开图柱、锥、台、球的体积3.2点、线、面之间的位置关系平面的基本性质空间两条直线的位置关系直线与平面的位置关系平面与平面的位置关系第4章平面解析几何初步 4.1直线与方程直线的斜率直线的方程两条直线的平行与垂直两条直线的交点平面上两点间的距离点到直线的距离4.2圆与方程圆的方程直线与圆的位置关系圆与圆的位置关系4.3空间直角坐标系空间直角坐标系空间两点间的距离高一数学下数学3第5章算法初步5.1算法的意义5.2流程图5.3基本算法语句5.4算法案例第6章统计6.1抽样方法6.2总体分布的估计6.3总体特征数的估计6.4线性回归方程第7章概率7.1随机事件及其概率 7.2古典概型7.3几何概型7.4互斥事件及其发生的概率数学4第8章三角函数8.1任意角、弧度8.2任意角的三角函数8.3三角函数的图象和性质第9章平面向量9.1向量的概念及表示9.2向量的线性运算9.3向量的坐标表示9.4向量的数量积9.5向量的应用第10章三角恒等变换10.1两角和与差的三角函数10.2二倍角的三角函数10.3几个三角恒等式高二数学上数学5第11章解三角形11．1正弦定理11．2余弦定理11．3正弦定理、余弦定理的应用第12章数列12．1等差数列12．2等比数列12．3数列的进一步认识第13章不等式13．1不等关系13．2一元二次不等式13．3二元一次不等式组与简单的线性规划问题 13．4基本不等式文科数学选修系列11-1上第1章常用逻辑用语1．1命题及其关系1．2简单的逻辑联结词1．3全称量词与存在量词第2章圆锥曲线与方程2．1圆锥曲线2．2椭圆2．3双曲线2．4抛物线2．5圆锥曲线与方程第3章导数及其应用3．1导数的概念3．2导数的运算3．3导数在研究函数中的应用3．4导数在实际生活中的应用1-2下第1章统计案例1．1假设检验1．2独立性检验1．3线性回归分析1．4聚类分析第2章推理与证明2．1合情推理与演绎推理2．2直接证明与间接证明2．3公理化思想第3章数系的扩充与复数的引入 3．1数系的扩充3．2复数的四则运算3．3复数的几何意义第4章框图4．1流程图5．2结构图理科数学选修系列22-1上第1章常用逻辑用语1．1命题及其关系1．2简单的逻辑连接词1．3全称量词与存在量词第2章圆锥曲线与方程第3章空间向量与立体几何2-2上第1章导数及其应用第2章推理与证明第3章数系的扩充与复数的引入 2-3下第1章计数原理第2章概率第3章统计案例。

江西省南康中学2012-2013学年高二理科数学周测卷（三）一、选择题（10×5分＝50分）1、6个不同的元素排成前后两排，每排3个元素，那么不同的排法种数是（ ）A ．36B ．120C ．720D ．1440 2、在(1)()n x n N +∈+的二项展开式中，若只有含5x 项的系数最大，则n 等于（ ）A ．8B ．9C ．10D ．11 3、51()x x-的二项展开式中含3x 项的系数为（ ） A ．5- B ．5 C ．10 D ．254、若多项式31091001910(1)(1)(1)x x a a x a x a x +=+++++++ ，则9a 等天（ ）A ．9B ．10C ．9-D ．10-5、A 、B 、C 、D 、E 五人并排站成一排，如果A 、B 必须相邻且B 在A 的右边，那么不同的排法有（ ）A ．60种B ．48种C ．36种D ．24种6、下列哪种情况有把握说明两个事件x 与y 之间无关（ ）A ．212x >B ．210x <C ．23x >D ．22.5x < 7、如果随机变量1(6,)2x B ，则(3)P x =等于（ ）A ． 516B ．58C ．316D ．7168、已知甲、乙两个学生每人回答一个问题，答对的概率分别为23和34，两人之间回答问题相互独立，则这两人中恰有一人答对的概率为（ ） A ．12 B ．512 C ．14 D ．169、点(1,P 的极坐标是（ ）A ．(2,)3πB ．4(2,)3πC ．(2,)3π- D ．4(2,)3π- 10、极坐标方程cos()4πρθ=-表示的曲线是（ ） A ．双曲线 B ．椭圆 C ．抛物线 D ．圆二、填空题11、已知函数91()(1)f x x =-，则()f x '中31x 的系数为 12、121393n n n n n C C C ++++=13、设随机变量x 的分布列为()(1,2)k P x k k λ===，则λ=14、已知A 、B 、C 相互独立，若111(),(),()688P AB P BC P ABC ===，则()P B = 15、极坐标方程24sin52θρ=化为直角坐标方程是三、解答题16、7个人排成一排，在下列情况下，各有多少种不同的排法？⑴甲不在排头，也不在排尾；⑵甲、乙之间有且只有2个人；⑶甲、乙、丙三人两两不相邻； ⑷甲在乙的左边（不一定相邻）17、已知在n 的展开式中，前三项的系数成等差数列.⑵求展开中所有的有理项.18、某蓝球运动员每次投篮命中的概率为23，且各次投篮的结果相互不影响.⑴假设这名运动员投篮5次，求恰有2次投中的概率；⑵假设这名运动员投篮5次，求有3次连续投中，别外2次未投中的概率.19、已知x 是离散型随机变量，x 取值为12,x x ，11()2P x x ==，21()2P x x ==，若12EX =，14DX =，求2212x x +.20、ABC ∆的底边10BC =，12A B ∠=∠，以B 为极点，BC 为极轴，求顶点A 的轨迹方程. 21、在平面直角坐标系中，已知点(3,0)A ， P 是圆221x y +=上一个动点， AOP ∠的平分线交PA 于点Q ，求Q 的轨迹的极坐标方程.。

学校： 班级： 姓名： 考生号：第三周周清题（复数及推理与证明）一、选择题 1、 下列表述正确的是（ ）.①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理；③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理；⑤类比推理是由特殊到特殊的推理. A ．①②③； B ．②③④； C ．②④⑤； D ．①③⑤.2、下面使用类比推理正确的是 （ ）. A.“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =”a B.“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅” C.“若()a b c ac bc +=+” 类推出“a b a b cc c+=+ （c ≠0）”D.“n n a a b =n （b ）” 类推出“n n a a b +=+n （b ）”3、 有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线b ⊆/平面α，直线a ≠⊂平面α，直线b ∥平面α，则直线b ∥直线a ”的结论显然是错误的，这是因为 （ ） A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误4、用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（ ） (A)假设三内角都不大于60度； (B) 假设三内角都大于60度；(C) 假设三内角至多有一个大于60度； (D) 假设三内角至多有两个大于60度。

5、若22(1)(32)x x x i -+++是纯虚数，则实数x 的值是（ ） A 1 B 1- C 1± D 以上都不对 6、复数911⎪⎭⎫⎝⎛+-i i 的值等于（ ） （A ）22 （B ）2 （C ）i （D ）i - 7、已知集合M=｛1,i m m m m )65()13(22--+--｝，N ＝｛1，3｝，M ∩N ＝｛1,3｝，则实数m 的值为（ ）（A ） 4 （B ）－1 （C ）4或－1 （D ）1或6 8、设复数z 满足条件,1=z 那么i z ++22的最大值是（ ）（A ）3 （B ）4 （C ）221+ （D ）32二、填空题 9、已知复数z 1=3+4i, z 2=t+i,,且z 1·2z 是实数,则实数t 等于 。

高二数学周周清（二项式定理、古典概型与分布列）一、选择题1.从数字1，2，3，4，5，中，随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于9的概率为 （ ）A ．12513 B ．12516 C ．12518 D ．125192.从1，2，……，9这九个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是A ．95B ．94C ．2111 D ．21103．在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521 的数共有 （ ） A ．56个 B ．57个 C ．58个 D ．60个4. 连续掷两次骰子，以先后得到的点数m 、n 为点P （m ，n ）的坐标，那么点P 在圆x 2+y 2＝17外部的概率应为（ ） （A ）31 （B ）32 （C ）1811 （D ）18135. 从全体3位正整数中任取一数，则此数以2为底的对数也是正整数的概率为A.2251 B.3001C.4501 D.以上全不对6. 有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（ ）（A ）13（B ）12（C ）23（D ）347. 若20112011012011(12),()x a a x a xx R -=++⋅⋅⋅+∈，则20111222011222a a a ++⋅⋅⋅+的值为（）A .2B .0C .1- D.2-8.两个骰子的点数分别为b 、c ，则方程x 2＋bx ＋c ＝0有两个实根的概率为 ( )A.12B.1536C.1936D.56 二、填空题9.若在二项式（x +1）10的展开式中任取一项,则该项的系数为奇数的概率是 . （结果用分数表示） 10.设()x a a x a x a x2122101221-1=+++L ，则1011a a -= .(结果用组合数表示)11.62x x ⎛⎫- ⎪⎝⎭展开式中不含2x 项的系数和为__________.12. 已知函数)2(,)2(2)(3f n x f x x f '='+-=,则二项式nxx )2(+展开式中常数 ．（用组合数表示）三、解答题1. 从4名男生和2名女生中任选3人参加演讲比赛.（Ⅰ）求所选3人都是男生的概率；（Ⅱ）求所选3人中恰有1名女生的概率；（Ⅲ）求所选3人中至少有1名女生的概率. (2004年天津卷)2. 设A＝{(x，y)|1≤x≤6,1≤y≤6，x，y∈N*}．(1)求从A中任取一个元素是(1,2)的概率；(2)从A中任取一个元素，求x＋y≥10的概率；(3)设ξ为随机变量，x yξ=-，求ξ的分布列3.掷一枚硬币，记1()1()ia⎧=⎨-⎩正面朝上反面朝上1,2,3,4i=设1234a a a aξ=+++Ⅰ求当0ξ=时的概率Ⅱ求ξ的分布列。