3.2立体几何中的向量方法----空间距离

知识讲解空间向量在立体几何中的应用三——距离的计算距离是立体几何中一个重要的概念，用来描述两个点、线或平面之间的远近关系。

在立体几何中，可以使用空间向量的知识来计算距离。

本篇文章将介绍三种常见的空间向量在立体几何中计算距离的方法。

第一种方法是点到点距离的计算。

设立体空间中有两个点A(x1,y1,z1)和B(x2,y2,z2)，则点A到点B的距离可以通过空间向量表示为：AB=√((x2-x1)²+(y2-y1)²+(z2-z1)²)例如，如果点A的坐标是(1,2,3)，点B的坐标是(4,5,6)，则点A到点B的距离为：AB=√((4-1)²+(5-2)²+(6-3)²)=√(3²+3²+3²)=√(27)≈5.196第二种方法是点到直线距离的计算。

设立体空间中有一条直线L和一个点P(x0,y0,z0)，要计算点P到直线L的距离，可以通过先计算点P到直线上的一点Q的距离，再计算点Q到直线上的两个点A和B的距离，其计算公式为：d(P,L)=AB=，PP_A×PP_B，/，A-B其中，×表示两个向量的叉乘运算，，表示向量的模，P_A和P_B分别是点P到直线上的两个垂足点。

第三种方法是点到平面距离的计算。

设立体空间中有一个平面平面α和一个点P(x0,y0,z0)，要计算点P到平面α的距离，可以通过计算点P到平面上的一点Q的距离，其计算公式为：d(P,α)=PQ·n/，n其中，·表示两个向量的点乘运算，n表示平面的法向量。

需要注意的是，当计算点到直线或点到平面的距离时，我们需要先确定直线或平面上的一个点，然后再计算该点到目标点的距离。

综上所述，空间向量在立体几何中的应用可以帮助我们计算点到点、点到直线和点到平面的距离。

这些计算方法在实际问题中非常有用，例如计算物体的尺寸、相机的视距等等。

§立体几何中的向量方法(三)——利用向量方法求距离知识点一求两点间的距离已知矩形ABCD中，AB＝4，AD＝3，沿对角线AC折叠，使面ABC 与面ADC 垂直，求BD 间的距离．解 方法一过D 和B 分别作DE ⊥AC 于E ，BF ⊥AC 于F ，则由已知条件可知AC ＝5，∴DE ＝3×45＝125，BF ＝3×45＝125.∵AE ＝AD 2AC ＝95＝CF ，∴EF ＝5－2×95＝75，∴DBu u u r ＝DE →＋EF u u u r ＋FB→. |DBu u u r|2＝ (DE →＋B 1E →＋FB →)2＝DE →2＋EF u u u r 2＋FB →2＋2DE →·EF u u u r ＋2DE →·FB →＋2EF u u u r ·FB →.∵面ADC ⊥面ABC ，而DE ⊥AC ，∴DE ⊥面ABC ， ∴ DE ⊥BF, DE→ ⊥FB →, |DBu u u r|2＝DE →2＋B 1E →2＋FB →2＝14425＋4925＋14425＝33725， ∴|DBu u u r |＝3375.故B 、D 间距离是3375. 方法二同方法一．过E 作FB 的平行线EP ，以E 为坐标原点，以EP ，EC ，ED 所在直线分别为x 、y 、z 轴建立空间直角坐标系如图．则由方法一知DE ＝FB ＝125，EF ＝75，∴D ⎝ ⎛⎭⎪⎫0，0，125，B ⎝ ⎛⎭⎪⎫125，75，0，∴BD u u u r＝⎝ ⎛⎭⎪⎫125，75，－125，| BDu u u r|＝⎝ ⎛⎭⎪⎫1252＋⎝ ⎛⎭⎪⎫752＋⎝⎛⎭⎪⎫－1252＝3375. 【反思感悟】 求两点间的距离或某线段的长度的方法： (1)把此线段用向量表示，然后用|a |2＝a·a 通过向量运算去求|a |.(2)建立空间坐标系，利用空间两点间的距离公式d ＝x 1－x 22＋y 1－y 22＋z 1－z 22求解．如图所示，正方形ABCD，ABEF的边长都是1，而且平面ABCD⊥平面ABEF，点M在AC上移动，点N在BF上移动，若CM＝BN＝a(0＜a ＜2)．(1)求MN的长；(2)当a为何值时，MN的长最小．解(1)建立如图所示的空间直角坐标系，则A(1,0,0)，F(1,1,0)，C(0,0,1)∵CM＝BN＝a(0<a<2)，且四边形ABCD、ABEF为正方形，∴M(22a,0,1－22a)，N(22a，22a,0)，∴|MN→＝(0，22a，22a－1)，∴|MN→|＝a2－2a＋1.(2)由(1)知MN＝a－222＋12，所以，当a＝22时，MN＝22.即M、N分别移到AC、BF的中点时，MN的长最小，最小值为2 2.知识点二求异面直线间的距离如图所示，在三棱柱ABC—A1B1C1中，AB⊥侧面BB1C1C，E为棱CC1上异于C、C1的一点，EA⊥EB1，已知AB＝2，BB1＝2，BC＝1，∠BCC1＝π3，求异面直线AB与EB1的距离．→、BA→所在直线分解.以B为原点，BA别为y、z轴，如图建立空间直角坐标系．由于BC ＝1，BB 1＝2，AB ＝2，∠BCC 1＝π3，在三棱柱ABC —A 1B 1C 1中有B(0,0,0)，A(0,0，2)，B 1(0,2,0)，设 E (3,,02a )，由EA ⊥EB 1，得EAu u u r ·1EB u u u r =0， 即⎝ ⎛⎭⎪⎪⎫－32，－a ，2·⎝ ⎛⎭⎪⎪⎫－32，2－a ，0＝0， 得⎝ ⎛⎭⎪⎫a －12⎝ ⎛⎭⎪⎫a －32＝0，即a ＝12或a ＝32(舍去)，故E ⎝ ⎛⎭⎪⎪⎫32，12，0.设n 为异面直线AB 与EB 1公垂线的方向向量，由题意可设n ＝(x ，y,0)，则有n ·1EB u u u r=0. 易得n ＝(3，1,0)，∴两异面直线的距离d ＝BE n n⋅u u u r＝⎪⎪⎪⎪⎪⎪⎪⎪⎝⎛⎭⎪⎪⎫32，12，0·3，1，03＋1＝1.【反思感悟】 求异面直线的距离，一般不要求作公垂线，若公垂线存在，则直接求解即可；若不存在，可利用两异面直线的法向量求解．如图所示，在长方体ABCD —A 1B 1C 1D 1中，AB ＝4，AD ＝3，AA 1＝2，M 、N 分别为DC 、BB 1的中点，求异面直线MN 与A 1B 的距离．解 以A 为原点，AD 、AB 、AA 1所在直线分别为x ，y ，z 轴建立空间直角坐标系，则A 1(0,0,2)，B(0,4,0)，M(3,2,0)，N(0,4,1)．∴|MN →＝(－3,2,1)，1A B u u u u r ＝(0,4，－2)．设MN 、A 1B 公垂线的方向向量为n ＝(x ，y ，z)， 则10,0,n MN n A B ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u u r即⎩⎪⎨⎪⎧－3x ＋2y ＋z ＝04y －2z ＝0.令y ＝1，则z ＝2，x ＝43， 即n ＝⎝ ⎛⎭⎪⎫43，1，2，|n |＝613.1MA u u u u r ＝(－3，－2,2)在n 上的射影的长度为d ＝1MA n nu u u u r ,故异面直线MN 与A 1B 的距离为66161.知识点三 求点到平面的距离在三棱锥B —ACD 中，平面ABD ⊥平面ACD ，若棱长AC ＝CD ＝AD ＝AB ＝1，且∠BAD ＝30°，求点D 到平面ABC 的距离．解如图所示，以AD 的中点O 为原点，以OD 、OC 所在直线为x 轴、y 轴，过O 作OM ⊥面ACD 交AB 于M ，以直线OM 为z 轴建立空间直角坐标系，则A ⎝ ⎛⎭⎪⎫－12，0，0，B ⎝ ⎛⎭⎪⎪⎫3－12，0，12， C ⎝ ⎛⎭⎪⎪⎫0，32，0，D ⎝ ⎛⎭⎪⎫12，0，0，∴AC u u u r=⎝ ⎛⎭⎪⎪⎫12，32，0，AB u u u r＝⎝ ⎛⎭⎪⎪⎫32，0，12，DC u u u r ＝⎝ ⎛⎭⎪⎪⎫－12，32，0， 设n ＝(x ，y ，z)为平面ABC 的一个法向量，则1·0,21·0,2AB x z AC x y ⎧⎫=+=⎪⎪⎪⎪⎨⎪⎪==⎪⎪⎩⎭n n u u u r u u u r ，∴y ＝－33x ，z ＝－3x ，可取n ＝(－3，1,3)，代入d ＝DC nn ⋅u u u r ，得d ＝32＋3213＝3913，即点D 到平面ABC 的距离是3913.【反思感悟】 利用向量法求点面距，只需求出平面的一个法向量和该点与平面内任一点连线表示的向量，代入公式求解即可．正方体ABCD —A 1B 1C 1D 1的棱长为4，M 、N 、E 、F 分别为A 1D 1、A 1B 1、C 1D 1、B 1C 1的中点，求平面AMN 平面与EFBD 间的距离.解 如图所示，建立空间直角坐标系D —xyz ，则A(4,0,0)，M(2,0,4)，D(0,0,0)，B(4,4,0)，E(0,2,4)，F(2,4,4)，N(4,2,4)，从而EFu u u r＝(2,2,0)，MN→＝(2,2,0)， AMu u u u r ＝(－2,0,4)，BF →＝(－2,0,4)， ∴EFu u u r ＝MN→， AMu u u u r＝BF→， ∴EF ∥MN ，AM ∥BF ，∴平面AMN ∥平面EFBD. 设n ＝(x ，y ，z)是平面AMN 的法向量，从而·220,·240,MN x y AM x z ⎧⎫=+=⎪⎪⎨⎪=-+=⎪⎩⎭n n u u u u r u u u u r解得⎩⎪⎨⎪⎧x ＝2zy ＝－2z.取z ＝1，得n ＝(2，－2,1)， 由于ABu u u r 在n 上的投影为n AB n⋅u u u r＝－84＋4＋1＝－83.∴两平行平面间的距离d ＝n AB n⋅u u u r ＝83.课堂小结：1．求空间中两点A ，B 的距离时，当不好建系时利用|AB|＝|AB u u u r|＝x 1－x 22＋y 1－y 22＋z 1－z 22来求． 2．两异面直线距离的求法．如图(1)，n 为l 1与l 2的公垂线AB 的方向向量，d ＝|AB u u u r|＝|CD →·n ||n |.3点B 到平面α的距离：|BOuuu r|=AB n n⋅u u u r .(如图(2)所示)4.面与面的距离可转化为点到面的距离.一、选择题1.若O 为坐标原点，OAu u u r=（1，1，-2），OB uuu r=（3，2，8），OCu u u r =（0，1，0），则线段AB 的中点P 到点C 的距离为（ ）B ．214答案 D解析 由题意OP uuu r ＝(1－t )OA →＝12(OA →＋OB →)＝(2，32，3)， PC →＝OC →－OP uuu r ＝(1－t )OA →＝(－2，－12，－3)，PC ＝|PC →|＝ 4＋14＋9＝532.2．如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，O 是底面A 1B 1C 1D 1的中心，则O 到平面ABC 1D 1的距离是( )A ．12答案 B解析 以D 为坐标原点，以DA ，DC ，DD 1所在直线分别为x,y,z 轴建立空间直角坐标系，则有D 1（0，0，1），D （0，0，0），A （1，0，0），B （1，1，0），A 1（1，0，1），C 1（0，1，1）.因O 为A 1C 1的中点，所以O （12，12,1），1C O u u u u r =（12， -12，0），设平面ABC 1D 1的法向量为 n=（x,y,z ），则有10,0,n AD n AB ⎧⋅=⎪⎨⋅=⎪⎩u u u u ru u u r即0,0,x z y -+=⎧⎨=⎩则 n = （1，0，1），∴O 到平面ABC 1D 1的距离为：1C O n d n⋅=u u u u r ,. 3．在直角坐标系中，设A (－2,3)，B (3，－2)，沿x 轴把直角坐标平面折成120°的二面角后，则A 、B 两点间的距离为( )A ．211 D ．311 答案 A解析 AB AE EF =+u u u r u u u r u u u r ＋FB→AB u u u r 2＝AE u u u r 2＋EF u u u r 2＋FB →2＋2AE u u u r ·EF u u u r ＋2AE u u u r ·FB →＋2EF u u u r ·FB →＝9＋25＋4＋2×3×2×12＝44.∴|AB u u u r|＝211.4．已知正方体ABCD —A 1B 1C 1D 1的棱长为2，点E 是A 1B 1的中点，则点A 到直线BE 的距离是( )答案 B解析 如图所示，BA u u u r=（2，0，0）， BE u u u r=（1，0，2）， ∴cos θ= BA BEBA BEu u u r u u u r u u u r u u u r＝225＝55， ∴sin θ＝1－cos 2θ＝255，A 到直线BE 的距离d ＝|－*6]·OC→|sin θ＝2×255＝455.二、填空题5．已知A (2,3,1)，B (4,1,2)，C (6,3,7)，D (－5，－4,8)，则点D 到平面ABC 的距离为________．答案 491717解析 设平面ABC 的法向量为n ＝(x ，y ，z )， 则0,0,n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u ur 即⎩⎪⎨⎪⎧(x ，y ，z )·(2，－2，1)＝0，(x ，y ，z )·(4，0，6)＝0.∴n ＝⎝ ⎛⎭⎪⎫－32，－1，1，又ADu u u r =（-7，-7，7）. ∴点D 到平面ABC 的距离d =AD n n⋅u u u r＝491717.6．在正方体ABCD —A 1B 1C 1D 1中，棱长为2，E 为A 1B 1的中点，则异面直线D 1E 和BC 1间的距离是________．答案 263解析 如图所示建立空间直角坐标系,设n 为异面直线D1E 与BC1公垂线的方向向量,并设n =(x,y,z),则有110,0,n BC n D E ⎧⋅=⎪⎨⋅=⎪⎩u u u u ru u u u r易求得n =（1， -2，1），∴d=11D C n n⋅u u u u u r＝|(0，2，0)·(1，－2，1)|1＋4＋1＝46＝263.7．在棱长为a 的正方体ABCD —A 1B 1C 1D 1中，点A 到平面A 1BD 的距离为________．答案 33a解析 以D 为空间直角坐标原点，以DA 、DC 、DD 1所在直线分别为x 轴、y 轴、z 轴建立坐标系，则D (0,0,0)，A (a,0,0)，B (a ，a,0)，A 1(a,0，a )．设n ＝(x ，y ，z )为平面A 1BD 的法向量，则有10,0,n DA n DB ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u r ，即⎩⎪⎨⎪⎧(x ，y ，z )(a ，0，a )＝0，(x ，y ，z )(a ，a ，0)＝0.∴⎩⎪⎨⎪⎧x ＋z ＝0，x ＋y ＝0，令x ＝1，∴n ＝(1，－1，－1)．∴点A 到平面A 1BD 的距离d ＝DA nn ⋅u u u r ＝a 3＝33a .三、解答题8．如图所示的多面体是由底面为ABCD 的长方体被截面AEC 1F 所截而得到的，其中AB ＝4，BC ＝2，CC 1＝3，BE ＝1.(1)求BF 的长；(2)求点C到平面AEC1F的距离．解(1)建立如图所示的空间直角坐标系，则D(0,0,0)，B(2,4,0)，A(2,0,0)，C(0,4,0)，E(2,4,1)，C1(0,4,3)．设F(0,0，z)．∵四边形AEC1F为平行四边形，u u u r u u u u r∴由1AF EC得（-2，0，z）=（-2，0，2），∴z=2.∴F（0，0，2）.∴BF u u u r=（-2，-4，2）.于是|BF u u u r|=26（2）设n1为平面AEC1F的一个法向量，显然n1不垂直于平面ADF，故可设n1=（x，y，1），由0,0,n AE n AF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r得 0410,2020,x y x y ⨯+⨯+=⎧⎨-⨯+⨯+=⎩ 即410,220,y x +=⎧⎨-+=⎩∴1,1,4x y =⎧⎪⎨=-⎪⎩∴n 1=（1,14-,1）.又1CC u u u u r=(0,0,3),设1CC u u u u r与n 1的夹角为α,则 cos α= 1111CC nCC n ⋅u u u u ru u u u r43313331116==⋅++∴C 到平面AEC 1F 的距离为d=|1CC u u u u r |cos α=3×43333433=9．已知：正四棱柱ABCD —A 1B 1C 1D 1中，底面边长为22，侧棱长为4，E 、F 分别为棱AB 、BC 的中点．(1)求证：平面B 1EF ⊥平面BDD 1B 1； (2)求点D 1到平面B 1EF 的距离． (1)证明建立如右图所示的空间直角坐标系，则D(0,0,0)，B(22，22，0)，E(22，2，0)， F(2，22，0)，D 1(0,0,4)， B 1(22，22，4)．EFu u u r ＝(－2，2，0)， DB→＝(22，22，0)，1DD u u u u r ＝(0,0,4)，EFu u u r·DB→＝0. ∴EF ⊥DB ，EF ⊥DD 1，DD 1∩BD ＝D ， ∴EF ⊥平面BDD 1B 1.又EF ⊂平面B 1EF ，∴平面B 1EF ⊥平面BDD 1B 1.（2）解由（1）知11D B u u u u r =)(22,2,0EFu u u r =)(2,2,0-，1B Eu u u u r =)(0,2,4--,设平面B 1EF 的法向量为n ,且n = (x,y,z)，则n ⊥EF u u u r ,n⊥1B Eu u u u r ，即n ·EF u u u r =（x ，y ，z ）·)(2,2,0＝－2x＋2y ＝0， n ·1B E u u u u r＝(x ，y ，z)·(0，－2，－4)＝－2y －4z ＝0.令x ＝1，则y ＝1，z ＝－24，∴n ＝⎝ ⎛⎭⎪⎪⎫1，1，－24. ∴D 1到平面B 1EF 的距离 11D B nd n ⋅=u u u u r ＝|22＋22|12＋12＋⎝⎛⎭⎪⎪⎫－242＝161717 10．直四棱柱ABCD －A 1B 1C 1D 1的高为3，底面是边长为4且∠DAB ＝60°的菱形，AC ∩BD ＝O ，A 1C 1∩B 1D 1＝O 1，E 是O 1A 的中点．(1)求二面角O 1—BC －D 的大小； (2)求点E 到平面O 1BC 的距离． 解 (1)∵OO 1⊥平面AC ，∴OO 1⊥OA ，OO 1⊥OB ，又OA ⊥OB ， 建立如图所示的空间直角坐标系，∵底面ABCD 是边长为4，∠DAB=60°的菱形，∴，OB=2，则，B(0,2,0)，C(-，O 1(0,0,3)设平面O 1BC 的法向量为n 1=（x,y,z ），则n 1⊥1O B u u u u r ， n 1⊥1O C u u u u r,∴⎩⎪⎨⎪⎧2y －3z ＝0－23x －3z ＝0，若z ＝2，则x ＝－3，y ＝3， ∴n 1＝(－3，3,2)，而平面AC的法向量n2＝(0,0,3)∴cos〈n1，n2〉＝n1·n2|n1|·|n2|＝63×4＝12，设O1－BC－D的平面角为α，∴cosα＝12，∴α＝60°.故二面角O1－BC－D为60°.(2)设点E到平面O1BC的距离为d，∵E是O1A的中点，∴1EO u u u u r＝(－3，0，32)，则d=111EO nnu u u u r＝|(－3，0，32)·(－3，3，2)|(－3)2＋32＋22＝3 2∴点E到面O1BC的距离等于32.。

立体几何中的向量方法(二)——求空间角和距离【基础检测】1．思维辨析(在括号内打“√”或“×”)．(1)两直线的方向向量所成的角就是两条直线所成的角．( )(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．( ) (3)两个平面的法向量所成的角是这两个平面所成的角．( )(4)两异面直线夹角的范围是⎝⎛⎦⎤0，π2，直线与平面所成角的范围是⎣⎡⎦⎤0，π2，二面角的范围是[0，π]．( )2．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )A ．30°B ．60°C ．120°D ．150°3．正三棱柱(如右图，底面是正三角形的直棱柱)ABC －A 1B 1C 1的底面边长为2，侧棱长为22，则AC 1与侧面ABB 1A 1所成的角为__ __.4．二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB ．已知AB ＝4，AC ＝6，BD ＝8，CD ＝217，则该二面角的大小为__ __.5．P 是二面角α－AB －β棱上一点，分别在平面α，β上引射线PM ，PN ，如果∠BPM ＝∠BPN ＝45°，∠MPN ＝60°，那么二面角α－AB －β的大小为__ __.【例题精讲】题型一求异面直线所成的角用向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系；(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)两异面直线所成角的余弦等于两向量夹角余弦值的绝对值．【例1】(2017·江苏卷)如图，在平行六面体ABCD－A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1＝3，∠BAD＝120°.(1)求异面直线A1B与AC1所成角的余弦值；(2)求二面角B－A1D－A的正弦值．题型二求直线与平面所成的角利用向量法求线面角的方法(1)分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)．(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所成的锐角，取其余角就是斜线和平面所成的角．【例2】如图，长方体ABCD－A1B1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4.过点E，F的平面α与此长方体的底面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求直线AF与平面α所成角的正弦值．题型三求二面角求二面角最常用的方法就是分别求出二面角的两个半平面所在面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．【例3】(2017·浙江卷)如图，已知正四面体D－ABC(所有棱长均相等的三棱锥)，P，Q，R分别为AB，BC，CA上的点，AP＝PB，BQQC＝CRRA＝2.分别记二面角D－PR－Q，D－PQ－R，D－QR－P的平面角为α，β，γ，则()A．γ<α<βB．α<γ<βC．α<β<γD．β<γ<α【例4】(2017·北京卷)如图，在四棱锥P－ABCD中，底面ABCD为正方形，平面P AD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，P A＝PD＝6，AB＝4.(1)求证：M为PB的中点；(2)求二面角为B－PD－A的大小；(3)求直线MC与平面BDP所成角的正弦值．【例5】 (2017·全国卷Ⅱ)如图，四棱锥P －ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°，E 是PD 的中点．(1)证明：直线CE ∥平面P AB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M －AB －D 的余弦值．题型四 求空间距离求点面距一般有以下三种方法：①作点到面的垂线，点到垂足的距离即为点到平面的距离；②等体积法；③向量法．其中向量法在易建立空间直角坐标系的规则图形中较简便．【例6】 如图，三棱柱ABC －A 1B 1C 1中，CC 1⊥平面ABC ，AC ＝BC ＝12AA 1，D 是棱AA 1的中点，DC 1⊥BD ．(1)证明：DC 1⊥BC ；(2)设AA 1＝2，A 1B 1的中点为P ，求点P 到平面BDC 1的距离．。

§3.2立体几何中的向量方法（三>利用向量方法求距离-对点讲练知识点一求两点间的距离八〔I已知矩形ABCD中，AB = 4 , AD = 3,沿对角线AC折叠, ADC垂直，求BD间的距离.解方法一过D和B分别作DE丄AC于E, BF丄AC于F, 则由已知条件可知AC = 5,••• DE =错误！=错误！，BF =错误！=错误!.•/ AE =错误！=错误！= CF,• EF= 5 —2X错误！=错误！，-I =错误！+ -I +错误！.| -1 |2=（错误！+错误！+错误！ >2=错误！2+ -1 2+错误！2+ 错误！错误！+ 2 -1错误！.•••面ADC丄面ABC，而DE丄AC ,•DE 丄面ABC ,•DE丄BF,错误！丄错误！,| — |2=错误！2+错误！2+错误！2=错误！+错误！+错误！=错误！,• | 1 |=错误！.故B、D间距离是错误！.方法二同方法一.过E作FB的平行线EP,以E为坐标原点，以EP, EC, 为x、y、z轴建立空间直角坐标系如图.则由方法一知DE = FB =错误！，EF=错误！，• D错误！，B错误！，使面ABC与面2错误！•一 + 2 ED所在直线分别| -I 匸错误！=错误!.ABEF ，点M 在AC 上移动，点 N 在BF 上移动，若 CM = BN = a(O v a v 错误！ ＞.(1＞求MN 的长；(2＞当a 为何值时，MN 的长最小. 解(1＞建立如图所示的空间直角坐标系，则 A(1,0,0＞，F(1,1,0＞，C(0,0,1＞•/ CM = BN = a(0＜a ＜错误! ＞， 且四边形 ABCD 、ABEF 为正方形，••• M(错误！a,0,1 —错误!a ＞，N(错误! a ，错误!a,0＞， •••I 错误！ = (0，错误! a ，错误! a — 1＞，二|错误！ |=错误!. (2＞由(1＞知MN =错误！， 所以，当a =错误！时，MN =错误!.即M 、N 分别移到AC 、BF 的中点时，MN 的长最小，最小值为 错误!. 知识点二求异面直线间的距离U 如图所示，在三棱柱 ABC — 中，AB 丄侧面BBQ I C ，E 为棱CC i 上异于C 、C i 的一点，EA 丄EB i ，已知 AB =错误！，BB i = 2，BC = 1，Z BCC i =错误！，求异 面直线AB 与EB i 的距离.解.以B 为原点，错误！、错误！所在直线分别为 y 、z 轴，如图建立空间直角坐标系.由于 BC = I ，BB i = 2， AB =错误！，/ BCC i =错误！，在三棱柱 ABC — A i B i C i 中有 B(0,0,0＞，A(0,0，错误！＞，B i (0,2,0＞，即错误！错误！ = 0,【反思感悟】 求两点间的距离或某线段的长度的方法：(1＞把此线段用向量表示，然后用|af 二a a 通过向量运算去求 间坐标系，利用空间两点间的距离公式 d =错误！求解.如图所示，正方形ABCD , ABEF 的边长都是1，而且平面a |.(2＞建立空设E ( ＞，由EA ^EB ,得 凹•回=0,得错误！错误！ = 0,即a =错误！或a =错误！(舍去＞, 故E 错误！. 设n 为异面直线AB 与EB i 公垂线的方向向量， 由题意可设n = (x , y,0＞ , 则有 n • —! =0. 易得n =(错误！，1,0＞ ,•••两异面直线的距离 d = 工 =错误！ = 1.【反思感悟】 求异面直线的距离，一般不要求作公垂线，若公垂线存在，则直接求解即可；若不存在，可利用两异面直线的法向量求解.如图所示，在长方体 ABCD — A I B I C I D I 中，AB = 4，AD = 3，AA 1= 2，M 、N 分别为 DC 、BB I 的中点，求异面直线 MN 与A I B 的距离.解以A 为原点，AD 、AB 、AA 1所在直线分别为x ，y ，z 轴建立空间直角坐标系， 贝V A 1(0,0,2＞，B(0,4,0＞，M(3,2,0＞，N(0,4,1＞ . •I 错误! = (- 3,2,1＞，I = (0,4，- 2＞ . 设MN 、A 1B 公垂线的方向向量为 n = (x ，y ，z ＞，即错误!.令 y = 1,贝U z = 2，x =错误！， 即n =错误！，|n |=错误！.—1= (— 3，- 2,2＞在n 上的射影的长度为d= I ,故异面直线MN与A I B的距离为错误！.知识点三求点到平面的距离卜卫在三棱锥 B —ACD中，平面ABD丄平面ACD，若棱长AC = CD = AD = AB =1,且/ BAD = 30 °求点D到平面ABC的距离.解如图所示，以AD的中点0为原点，以0D、OC所在直线为x轴、y轴，过0作0M丄面ACD 交AB于M，以直线0M为z轴建立空间直角坐标系，则A错误！，B错误！，C错误！，D错误！，•••=错误！，-I =错误！，丨=错误！，设n = (x, y, z>为平面ABC的一个法向量，• y=—错误！ x, z=—错误！ x,可取n =(—错误！，1,3> ,代入d = □ ，得d=错误！=错误！，即点D到平面ABC的距离是错误！.【反思感悟】禾U用向量法求点面距，只需求出平面的一个法向量和该点与平面内任一点连线表示的向量，代入公式求解即可.正方体ABCD —A1B1C1D1 的棱长为4, M、N、E、F 分别为A1D1、A1B1、C1D1、B1C1的中点，求平面AMN平面与EFBD间的距离.解如图所示，建立空间直角坐标系 D —xyz，贝U A(4,0,0> , M(2,0,4> , D(0,0,0> ,B(4,4,0> , E(0,2,4> , F(2,4,4> , N(4,2,4> ,从而一 =(2,2,0> ,错误！= (2,2,0>,I亠=(—2,0,4>,错误！= (- 2,0,4>,二一I =错误！，I亠=错误！，••• EF // MN , AM // BF ,•••平面AMN //平面EFBD.设n = (x, y, z>是平面AMN的法向量，解得错误！•取z = 1 得n = (2, —2,1>,由于一在n上的投影为|创=错误！=—错误！.•两平行平面间的距离课堂小结：1. 求空间中两点A , B的距离时，当不好建系时利用|AB| |=错误！来求.2. 两异面直线距离的求法.如图(1>, n为l i与12的公垂线AB的方向向量, d=|」匸错误！.图⑴3点B到平面a的距离：|•(如图(2>所示>4•面与面的距离可转化为点到面的距离课时作业-一、选择题1•若0 为坐标原点，口=<1 , 1 , 2) , —=<3 , 2, 8),-=<0, 1 , 0),则线段AB的中点P到点C的距离为<)A.错误！ B . 2错误！ C.错误！ D.错误！答案D解读由题意 I = (1 — t>错误！=错误！(错误！ +错误! > = (2,错误！，3>,错误！=错误！—二=(1 — t>错误！ = (— 2,—错误！，— 3> , PC = |错误! |=错误！=错误！ •2. 如图，正方体 ABCD — A i B i C i D i 的棱长为1 , O 是底面 A 1B 1C 1D 1的中心，贝V O 至U平面ABC 1D 1的距离是(>□ ______ C,EA •弐B.错误！C.错误！D.错误！ 答案B 解读以D 为坐标原点，以 DA , DC , DD 1所在直线分别为 x,y,z 轴建立空间直角坐标 系，则有 D 1<0, 0, 1), D<0 , 0, 0), A<1 , 0, 0), B<1 , 1 , 0), A 1<1 , 0, 1),C 1<0, 1, 1).因O 为A 1C 1的中点，所以 0<习，耳,1), 回=胡，口勺，0),设平面ABC 1D 1的法向量为n=<x,y,z )，则有则 n = <1 , 0, 1),••• O 到平面ABC 1D 1的距离为:3 .在直角坐标系中，设A(— 2,3> , B(3, — 2>,沿x 轴把直角坐标平面折成 120。

立体几何中的向量方法：空间距离问题（导学案）学习目标：1． 了解空间向量的表示方法，会用空间的一个基底表示空间任意一个向量；2． 理解空间向量的模和空间向量的投影与空间距离之间的关系，能运用向量的运算求解与空间距离有关的问题；3． 体会空间向量方法在研究空间距离问题时的重要作用。

学习重点：1、 立体几何问题中点到点的距离、点到面的距离、线到面的距离、点到线的距离、线到线的距离和面到面的距离；2、 法向量的确立以及向量在法向量方向上的投影。

教学难点：向量在法向量上的投影与空间距离之间的等价关系。

学习过程：1、 知识回顾（1） 向量数量积的运算：a ⃗∙b ⃗⃗=|a ⃗|∙|b ⃗⃗|∙cos 〈a ⃗,b⃗⃗〉 （2） a ⃗在b⃗⃗方向上的投影： 2、 知识迁移（1） OA⃗⃗⃗⃗⃗⃗在OB ⃗⃗⃗⃗⃗⃗向量方向上的投影： （2） AC⃗⃗⃗⃗⃗⃗在OB ⃗⃗⃗⃗⃗⃗向量方向上的投影： （3） A 、C 的距离与AC⃗⃗⃗⃗⃗⃗在OB ⃗⃗⃗⃗⃗⃗向量方向上的投影之间的关系： 3、 问题探究探究问题一：空间中点到点的距离如图1，已知斜四棱中以顶点A 为端点的三条棱长都相等，且它们彼此的夹角都是60°，那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系？练习1.正四面体OABC 的棱长为1，D 、E 分别是OA 、BC 的中点，连接DE ，求DE 的长.探究问题二：空间中点到面的距离、线到面的距离、面到面的距离如图，在正方体ABCD-A 1B 1C 1D 1中，棱长为1，E 为D 1C 1的中点，求: A E DC O A C 1 B CD 1A 1 DB 1（1）B 1到面A 1BE 的距离；（2）求D 1C 到面A 1BE 的距离；（3）面A 1DB 与面D 1CB 1的距离.及时小结：空间中点到面的距离、线到面的距离、面到面的距离，归纳起来，其本质都是点到面的距离。

探究问题三：空间中点到直线的距离、直线到直线的距离 如图，在正方体ABCD-A 1B 1C 1D 1中，棱长为1，E 为D 1C 1的中点，求 （1）点E 到直线A 1B 的距离；（2）直线D 1B 与A 1E 的距离.AC B 1 B A 1D E D 1 C 1A CB 1B A 1 D E D 1C 1 A C B 1 B A 1D D 1 C 1 A C B 1B A 1 D E D 1C 1。

3.2.3 利用空间向量求空间角、空间距离问题1．空间角及向量求法(1)两异面直线所成的角与两直线的方向向量所成的角相等．( )(2)直线l∥平面α，则直线l到平面α的距离就是直线l上的点到平面α的距离．( )(3)若平面α∥β，则两平面α，β的距离可转化为平面α内某条直线到平面β的距离，也可转化为平面α内某点到平面β的距离．( )答案 (1)× (2)√ (3)√2．做一做(请把正确的答案写在横线上)(1)已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角的大小为________．(2)(教材改编P 111A 组T 11)如图，在正方体ABCD －A 1B 1C 1D 1中，M 是C 1C 的中点，O 是底面ABCD 的中点，P 是A 1B 1上的任意点，则直线BM 与OP 所成的角为________．(3)已知平面α的一个法向量为n ＝(－2，－2,1)，点A (－1,3,0)在平面α内，则点P (－2,1,4)到平面α的距离为________．答案 (1)45°或135° (2)π2 (3)103解析 (2)建立如图所示的空间直角坐标系，设正方体棱长为2 ，则O (1,1,0)，P (2，x,2)，B (2,2,0)，M (0,2,1)，则OP→＝(1，x －1,2)，BM →＝(－2,0,1)．所以OP →·BM →＝0，所以直线BM 与OP 所成角为π2. 探究1 利用空间向量求线线角例1 如图1，已知两个正四棱锥P －ABCD 与Q －ABCD 的高分别为1和2，AB ＝4.求异面直线AQ 与PB 所成角的余弦值．[解] 由题设知，ABCD 是正方形，连接AC ，BD ，交于点O ，则AC ⊥BD .连接PQ ，则PQ 过点O .由正四棱锥的性质知PQ ⊥平面ABCD ，故以O 为坐标原点，以直线CA，DB，QP分别为x轴、y轴、z轴建立空间直角坐标系(如图2)，则P(0,0,1)，A(22，0,0)，Q(0,0，－2)，B(0,22，0)，∴AQ→＝(－22，0，－2)，PB→＝(0,22，－1)．于是cos〈AQ→，PB→〉＝AQ→·PB→|AQ→||PB→|＝39，∴异面直线AQ与PB所成角的余弦值为3 9 .拓展提升两异面直线所成角的求法(1)平移法：即通过平移其中一条(也可两条同时平移)，使它们转化为两条相交直线，然后通过解三角形获解．(2)取定基底法：在一些不适合建立坐标系的题型中，我们经常采用取定基底的方法，这是小技巧．在由公式cos〈a，b〉＝a·b|a||b|求向量a、b的夹角时，关键是求出a·b及|a|与|b|，一般是把a、b用一组基底表示出来，再求有关的量．(3)用坐标法求异面直线的夹角的方法①建立恰当的空间直角坐标系；②找到两条异面直线的方向向量的坐标形式；③利用向量的夹角公式计算两直线的方向向量的夹角；④结合异面直线所成角的范围得到异面直线所成的角．【跟踪训练1】如图，在三棱锥V－ABC中，顶点C在空间直角坐标系的原点处，顶点A，B，V分别在x，y，z轴上，D是线段AB 的中点，且AC ＝BC ＝2，∠VDC ＝θ.当θ＝π3时，求异面直线AC 与VD 所成角的余弦值．解 由于AC ＝BC ＝2，D 是AB 的中点，所以C (0,0,0)，A (2,0,0)，B (0,2,0)，D (1,1,0)．当θ＝π3时，在Rt △VCD 中，CD ＝2，故有V (0,0，6)．所以AC →＝(－2,0,0)，VD →＝(1,1，－6)．所以cos 〈AC →，VD →〉＝AC →·VD→|AC →||VD →|＝－22×22＝－24.所以异面直线AC 与VD 所成角的余弦值为24.探究2 利用空间向量求线面角例2 正三棱柱ABC －A 1B 1C 1的底面边长为a ，侧棱长为2a ，求AC 1与侧面ABB 1A 1所成的角．[解] 建立如下图所示的空间直角坐标系，则A (0,0,0)，B (0，a,0)，A 1(0,0, 2a )，C 1⎝⎛⎭⎪⎪⎫－32a ，a2， 2a ， 取A 1B 1的中点M ，则M ⎝⎛⎭⎪⎫0，a2，2a ，连接AM ，MC 1，有MC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，0，0， AB →＝(0，a,0)，AA1→＝(0,0，2a )．∴MC 1→·AB →＝0，MC 1→·AA 1→＝0， ∴MC 1→⊥AB →，MC1→⊥AA 1→， 即MC 1⊥AB ，MC 1⊥AA 1，又AB ∩AA 1＝A ， ∴MC 1⊥平面ABB 1A 1 .∴∠C 1AM 是AC 1与侧面A 1ABB 1所成的角．由于AC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，a 2，2a ，AM →＝⎝ ⎛⎭⎪⎫0，a 2，2a ，∴AC 1→·AM →＝0＋a 24＋2a 2＝9a 24，|AC 1→|＝3a 24＋a 24＋2a 2＝3a ， |AM →|＝a 24＋2a 2＝32a ， ∴cos 〈AC1→，AM →〉＝9a 243a ×3a 2＝32. ∴〈AC 1→，AM →〉＝30°，即AC 1与侧面ABB 1A 1所成的角为30°. [解法探究] 此题有没有其他解法？解 与原解建立相同的空间直角坐标系，则AB →＝(0，a,0)，AA1→＝(0,0，2a )，AC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，a 2，2a . 设侧面ABB 1A 1的法向量n ＝(λ，x ，y )，∴n ·AB →＝0且n ·AA1→＝0.∴ax ＝0且2ay ＝0.∴x ＝y ＝0.故n ＝(λ，0,0)．∵AC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，a 2，2a ， ∴cos 〈AC 1→，n 〉＝n ·AC1→|n ||AC 1→|＝－λ2|λ|.∴|cos 〈AC 1→，n 〉|＝12. ∴AC 1与侧面ABB 1A 1所成的角为30°.[条件探究] 此题中增加条件“E ，F ，G 为AB ，AA 1，A 1C 1的中点”，求B 1F 与平面GEF 所成角的正弦值．解 建立如图所示的空间直角坐标系，则B 1(0，a ，2a )，E ⎝ ⎛⎭⎪⎫0，a 2，0，F ⎝ ⎛⎭⎪⎪⎫0，0，22a ，G ⎝⎛⎭⎪⎪⎫－34a ，a 4，2a ， 于是B 1F →＝⎝ ⎛⎭⎪⎪⎫0，－a ，－22a ，EF →＝⎝ ⎛⎭⎪⎪⎫0，－a 2，22a ， EG →＝⎝ ⎛⎭⎪⎪⎫－34a ，－a 4，2a . 设平面GEF 的法向量n ＝(x ，y ，z )，则⎩⎨⎧n ·EF →＝0，n ·EG →＝0，即⎩⎪⎨⎪⎧－a 2y ＋22az ＝0，－34ax －a 4y ＋2az ＝0，所以⎩⎪⎨⎪⎧y ＝2z ，x ＝6z ，令z ＝1，得x ＝6，y ＝2，所以平面GEF 的一个法向量为n ＝(6，2，1)， 所以|cos 〈B 1F →，n 〉|＝|n ·B 1F →||n ||B 1F →|＝⎪⎪⎪⎪⎪⎪⎪⎪－2a －22a 9×a 2＋a 22＝33. 所以B 1F 与平面GEF 所成角的正弦值为33.拓展提升求直线与平面的夹角的方法与步骤思路一：找直线在平面内的射影，充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值)．思路二：用向量法求直线与平面的夹角可利用向量夹角公式或法向量．利用法向量求直线与平面的夹角的基本步骤：(1)建立空间直角坐标系； (2)求直线的方向向量AB →； (3)求平面的法向量n ；(4)计算：设线面角为θ，则sin θ＝|n ·AB→||n ||AB→|.【跟踪训练2】 如图，四棱锥P －ABCD 中，PA ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，PA ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点．(1)证明：MN ∥平面PAB ；(2)求直线AN 与平面PMN 所成角的正弦值．解 (1)证明：由已知得AM ＝23AD ＝2.取BP 的中点T ，连接AT ，TN .由N 为PC 的中点知TN ∥BC ，TN ＝12BC ＝2.又AD ∥BC ，故TN 綊AM ，四边形AMNT 为平行四边形，于是MN ∥AT .因为AT ⊂平面PAB ，MN ⊄平面PAB ，所以MN ∥平面PAB .(2)取BC 的中点E ，连接AE .由AB ＝AC 得AE ⊥BC ，从而AE ⊥AD ，且AE ＝AB 2－BE 2＝AB2－⎝ ⎛⎭⎪⎫BC 22＝ 5.以A 为坐标原点，AE →的方向为x 轴正方向，建立如图所示的空间直角坐标系Axyz .由题意知，P (0,0,4)，M (0,2,0)，C (5，2,0)，N ⎝⎛⎭⎪⎪⎫52，1，2， PM →＝(0,2，－4)，PN →＝⎝ ⎛⎭⎪⎪⎫52，1，－2，AN →＝⎝ ⎛⎭⎪⎪⎫52，1，2. 设n ＝(x ，y ，z )为平面PMN 的法向量，则⎩⎨⎧n ·PM →＝0，n ·PN →＝0，即⎩⎪⎨⎪⎧2y －4z ＝0，52x ＋y －2z ＝0，可取n ＝(0,2,1)．于是|cos 〈n ，AN →〉|＝|n ·AN →||n ||AN →|＝8525，则直线AN 与平面PMN所成角的正弦值为8525.探究3 利用空间向量求二面角例3 如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF ＝2FD ，∠AFD ＝90°，且二面角D －AF －E 与二面角C －BE －F 都是60°.(1)证明：平面ABEF⊥平面EFDC；(2)求二面角E－BC－A的余弦值．[解] (1)证明：由已知可得AF⊥DF，AF⊥FE，所以AF⊥平面EFDC.又AF⊂平面ABEF，故平面ABEF⊥平面EFDC.(2)过D作DG⊥EF，垂足为G，由(1)知DG⊥平面ABEF.以G为坐标原点，GF→的方向为x轴正方向，|GF→|为单位长，建立如图所示的空间直角坐标系Gxyz.由(1)知∠DFE为二面角D－AF－E的平面角，故∠DFE＝60°，则DF＝2，DG＝3，可得A(1,4,0)，B(－3,4,0)，E(－3,0,0)，D(0,0，3)．由已知，AB∥EF，AB⊄平面EFDC，EF⊂平面EFDC，所以AB∥平面EFDC.又平面ABCD∩平面EFDC＝CD，故AB∥CD，CD∥EF.由BE∥AF，可得BE⊥平面EFDC，所以∠CEF为二面角C－BE －F的平面角，∠CEF＝60°.从而可得C(－2,0，3)．连接AC，则EC→＝(1,0，3)，EB→＝(0,4,0)，AC→＝(－3，－4，3)，AB→＝(－4,0,0)．设n＝(x，y，z)是平面BCE的法向量，则⎩⎨⎧n ·EC →＝0，n ·EB →＝0，即⎩⎪⎨⎪⎧x ＋3z ＝0，4y ＝0，所以可取n ＝(3,0，－3)．设m 是平面ABCD 的法向量，则⎩⎨⎧m ·AC →＝0，m ·AB →＝0，同理可取m ＝(0，3，4)．则cos 〈n ，m 〉＝n ·m |n ||m |＝－21919.故二面角E －BC －A 的余弦值为－21919.拓展提升二面角的向量求法(1)若AB ，CD 分别是二面角α－l －β的两个半平面内与棱l 垂直的异面直线，则二面角的大小就是向量AB →与CD →的夹角(如图①)．(2)利用坐标法求二面角的步骤设n 1，n 2分别是平面α，β的法向量，则向量n 1与n 2的夹角(或其补角)就是两个平面夹角的大小，如图②.用坐标法的解题步骤如下：①建系：依据几何条件建立适当的空间直角坐标系． ②求法向量：在建立的坐标系下求两个面的法向量n 1，n 2.③计算：求n1与n2所成锐角θ，cosθ＝|n1·n2| |n1||n2|.④定值：若二面角为锐角，则为θ；若二面角为钝角，则为π－θ.【跟踪训练3】若PA⊥平面ABC，AC⊥BC，PA＝AC＝1，BC ＝2，求二面角A－PB－C的余弦值．解 解法一：如下图所示，取PB 的中点D ，连接CD .∵PC ＝BC ＝2，∴CD ⊥PB .∴作AE ⊥PB 于E ，那么二面角A －PB －C 的大小就等于异面直线DC 与EA 所成的角θ的大小．∵PD ＝1，PE ＝PA 2PB ＝12，∴DE ＝PD －PE ＝12，又∵AE ＝AP ·AB PB ＝32，CD ＝1，AC ＝1，AC →＝AE →＋ED →＋DC →，且AE →⊥ED →，ED →⊥DC→，∴|AC →|2＝|AE →|2＋|ED →|2＋|DC →|2＋2|AE →|·|DC →|·cos(π－θ)， 即1＝34＋14＋1－2×32×1×cos θ，解得cos θ＝33.故二面角A －PB －C 的余弦值为33.解法二：由解法一可知，向量DC →与EA →的夹角的大小就是二面角A －PB －C 的大小，如图，建立空间直角坐标系Cxyz ，则A (1,0,0)，B (0，2，0)，C (0,0,0)，P (1,0,1)，D 为PB的中点，D ⎝⎛⎭⎪⎪⎫12，22，12. ∵PE EB ＝AP 2AB 2＝13，即E 分PB →的比为13，∴E ⎝⎛⎭⎪⎪⎫34，24，34，EA →＝⎝ ⎛⎭⎪⎪⎫14，－24，－34， DC →＝⎝ ⎛⎭⎪⎪⎫－12，－22，－12，|EA →|＝32，|DC →|＝1，EA →·DC →＝14×⎝ ⎛⎭⎪⎫－12＋⎝ ⎛⎭⎪⎪⎫－24×⎝ ⎛⎭⎪⎪⎫－22＋⎝ ⎛⎭⎪⎫－34×⎝ ⎛⎭⎪⎫－12＝12.∴cos 〈EA →，DC →〉＝EA →·DC →|EA →||DC →|＝33. 故二面角A －PB －C 的余弦值为33.解法三：如右图所示，建立空间直角坐标系，则A (0,0,0)，B (2，1,0)，C (0,1,0)，P (0,0,1)，AP →＝(0,0,1)，AB →＝(2，1,0)，CB →＝(2，0,0)，CP →＝(0，－1,1)，设平面PAB 的法向量为m ＝(x ，y ，z )，则⎩⎨⎧m ·AP →＝0，m ·AB →＝0⇒⎩⎪⎨⎪⎧x ，y ，z ·0，0，1＝0，x ，y ，z ·2，1，0＝0⇒⎩⎪⎨⎪⎧y ＝－2x ，z ＝0，令x ＝1，则m ＝(1，－2，0)，设平面PBC 的法向量为n ＝(x ′，y ′，z ′)，则⎩⎨⎧n ·CB →＝0，n ·CP →＝0⇒⎩⎪⎨⎪⎧x ′，y ′，z ′·2，0，0＝0，x ′，y ′，z ′·0，－1，1＝0⇒⎩⎪⎨⎪⎧x ′＝0，y ′＝z ′.令y ′＝－1，则n ＝(0，－1，－1)，∴cos 〈m ，n 〉＝m ·n |m ||n |＝33.∴二面角A －PB －C 的余弦值为33.探究4 利用空间向量求距离例4 已知正方形ABCD 的边长为1，PD ⊥平面ABCD ，且PD ＝1，E ，F 分别为AB ，BC 的中点．(1)求点D 到平面PEF 的距离； (2)求直线AC 到平面PEF 的距离．[解] 解法一：(1)建立如图所示的空间直角坐标系，则D (0,0,0)，P (0，0,1)，A (1,0,0)，C (0,1,0)，E ⎝ ⎛⎭⎪⎫1，12，0，F ⎝ ⎛⎭⎪⎫12，1，0.设DH ⊥平面PEF ，垂足为H ，则DH →＝xDE →＋yDF →＋zDP →＝⎝ ⎛⎭⎪⎫x ＋12y ，12x ＋y ，z ·(x ＋y ＋z ＝1)，PE →＝⎝ ⎛⎭⎪⎫1，12，－1，PF →＝⎝ ⎛⎭⎪⎫12，1，－1.∴DH →·PE →＝x ＋12y ＋12⎝ ⎛⎭⎪⎫12x ＋y －z ＝54x ＋y －z ＝0.同理，DH →·PF →＝x ＋54y －z ＝0，又x ＋y ＋z ＝1，∴可解得x ＝y ＝417，z ＝917.∴DH →＝317(2,2,3)．∴|DH →|＝31717.因此，点D 到平面PEF 的距离为31717.(2)设AH ′⊥平面PEF ，垂足为H ′，则AH ′→∥DH →，设AH ′→＝λ(2,2,3)＝(2λ，2λ，3λ)(λ≠0)，则EH ′→＝EA →＋AH ′→＝⎝ ⎛⎭⎪⎫0，－12，0＋(2λ，2λ，3λ)＝⎝ ⎛⎭⎪⎫2λ，2λ－12，3λ.∴AH ′→·EH ′→＝4λ2＋4λ2－λ＋9λ2＝0，即λ＝117.∴AH ′→＝117(2,2,3)，|AH ′→|＝1717， 又AC ∥平面PEF ，∴AC 到平面PEF 的距离为1717.解法二：(1)由解法一建立的空间直角坐标系知EF →＝⎝ ⎛⎭⎪⎫－12，12，0，PE →＝⎝ ⎛⎭⎪⎫1，12，－1，DE →＝⎝ ⎛⎭⎪⎫1，12，0，设平面PEF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧－12x ＋12y ＝0，x ＋12y －z ＝0，解得⎩⎪⎨⎪⎧y ＝x ，z ＝32x ，令x ＝2，则n ＝(2,2,3)， ∴点D 到平面PEF 的距离d ＝|DE →·n ||n |＝|2＋1|4＋4＋9＝31717.(2)∵AC ∥EF ，∴直线AC 到平面PEF 的距离也即是点A 到平面PEF 的距离．又AE →＝⎝ ⎛⎭⎪⎫0，12，0，∴点A 到平面PEF 的距离为 d ＝|AE →·n ||n |＝117＝1717.拓展提升1.向量法求点到直线的距离的两种思路(1)将求点到直线的距离问题转化为求向量模的问题，即利用待定系数法求出垂足的坐标，然后求出向量的模，这是求各种距离的通法．(2)直接套用点线距公式求解，其步骤为直线的方向向量a →所求点到直线上一点的向量PP ′→及其在直线的方向向量a 上的投影→代入公式．注意平行直线间的距离与点到直线的距离之间的转化． 2．点面距、线面距、面面距的求解方法线面距、面面距实质上都是求点面距，求直线到平面、平面到平面的距离的前提是线面、面面平行．点面距的求解步骤：(1)求出该平面的一个法向量；(2)找出从该点出发的平面的任一条斜线段对应的向量； (3)求出法向量与斜线段对应向量的数量积的绝对值，再除以法向量的模，即可求出点到平面的距离．【跟踪训练4】 正方体ABCD －A 1B 1C 1D 1的棱长为2，E ，F ，G 分别是C 1C ，D 1A 1，AB 的中点，求点A 到平面EFG 的距离．解 如图，建立空间直角坐标系，则A (2,0,0)，E (0,2,1)，F (1,0,2)，G (2,1,0)，∴EF →＝(1，－2,1)，EG →＝(2，－1，－1)，GA →＝(0，－1,0)． 设n ＝(x ，y ，z )是平面EFG 的法向量，则⎩⎨⎧n ·EF →＝0，n ·EG →＝0，∴⎩⎪⎨⎪⎧x －2y ＋z ＝0，2x －y －z ＝0，∴x ＝y ＝z ，可取n ＝(1,1,1)， ∴d ＝|GA →·n ||n |＝13＝33，即点A 到平面EFG 的距离为33.探究5 与空间有关的探索性问题例5 如图，矩形ABCD 和梯形BEFC 所成的平面互相垂直，BE ∥CF ，∠BCF ＝∠CEF ＝90°，AD ＝3，EF ＝2.(1)求证：AE ∥平面DCF ；(2)当AB 的长为何值时，二面角A －EF －C 的大小为60°？[解] 如图，以点C 为坐标原点，以CB ，CF 和CD 所在直线分别作为x 轴、y 轴和z 轴，建立空间直角坐标系Cxyz .设AB ＝a ，BE ＝b ，CF ＝c ，则C (0,0,0)，A (3，0，a )，B (3，0,0)，E (3，b,0)，F (0，c,0)．(1)证明：AE →＝(0，b ，－a )，CB →＝(3，0,0)，BE →＝(0，b,0)，∴CB →·AE →＝0，CB →·BE →＝0， 从而CB ⊥AE ，CB ⊥BE . 又AE ∩BE ＝E ， ∴CB ⊥平面ABE . ∵CB ⊥平面DCF ，∴平面ABE ∥平面DCF .又AE ⊂平面ABE ， 故AE ∥平面DCF .(2)∵EF →＝(－3，c －b,0)，CE →＝(3，b,0)， 且EF →·CE →＝0，|EF→|＝2， ∴⎩⎪⎨⎪⎧－3＋b c －b ＝0，3＋c －b2＝2，解得b ＝3，c ＝4.∴E (3，3,0)，F (0,4,0)．设n ＝(1，y ，z )与平面AEF 垂直， 则n ·AE →＝0，n ·EF →＝0，即⎩⎪⎨⎪⎧1，y ，z ·0，3，－a ＝0，1，y ，z ·－3，1，0＝0，解得n ＝⎝⎛⎭⎪⎪⎫1，3，33a.又∵BA ⊥平面BEFC ，BA →＝(0,0，a )，∴|cos 〈n ，BA →〉|＝|n ·BA →||n ||BA →|＝334a 2＋27＝12， 解得a ＝92或a ＝－92(舍去)．∴当AB ＝92时，二面角A －EF －C 的大小为60°.拓展提升利用向量解决存在性问题的方法策略求解存在性问题的基本策略是：首先，假定题中的数学对象存在；其次，构建空间直角坐标系；再次，利用空间向量法把存在性问题转化为求参数是否有解问题；最后，解方程，下结论．利用上述思维策略，可使此类存在性难题变为常规问题．【跟踪训练5】 在长方体ABCD －A 1B 1C 1D 1中，AD ＝AA 1＝12AB ，点E 是棱AB 上一点，且AEEB＝λ. (1)证明：D 1E ⊥A 1D ；(2)是否存在λ，使得二面角D 1－EC －D 的平面角为π4？并说明理由．解 (1)证明：以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴建立空间直角坐标系，如图所示．不妨设AD ＝AA 1＝1，AB ＝2，则D (0,0,0)，A (1,0,0)，B (1,2,0)，C (0,2,0)，A 1(1,0,1)，B 1(1,2,1)，C 1(0,2,1)，D 1(0,0,1)．因为AEEB ＝λ，所以E ⎝⎛⎭⎪⎫1，2λ1＋λ，0， 于是D 1E →＝⎝ ⎛⎭⎪⎫1，2λ1＋λ，－1，A 1D →＝(－1,0，－1)，所以D 1E →·A 1D →＝⎝ ⎛⎭⎪⎫1，2λ1＋λ，－1·(－1,0，－1)＝－1＋0＋1＝0，故D 1E ⊥A 1D .(2)因为DD 1⊥平面ABCD ，所以平面DEC 的一个法向量为n ＝(0,0,1)，设平面D 1EC 的法向量为n 1＝(x ，y ，z )，又CE →＝⎝ ⎛⎭⎪⎫1，2λ1＋λ－2，0，CD 1→＝(0，－2,1)， 则⎩⎨⎧n 1·CE →＝0，n 1·CD 1→＝0，即⎩⎪⎨⎪⎧n 1·⎝ ⎛⎭⎪⎫1，2λ1＋λ－2，0＝0，n 1·0，－2，1＝0，整理得⎩⎪⎨⎪⎧x －y ·21＋λ＝0，－2y ＋z ＝0，取y ＝1，则n 1＝⎝ ⎛⎭⎪⎫21＋λ，1，2. 因为二面角D 1－EC －D 的平面角为π4，所以22＝|n ·n 1||n ||n 1|，即22＝21＋4＋⎝⎛⎭⎪⎫21＋λ2，解得λ＝233－1. 故存在λ＝233－1，使得二面角D 1－EC －D 的平面角为π4.1.用空间向量解决立体几何问题的“三步曲”(1)建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线，把立体几何问题转化为向量问题.(2)通过向量运算，研究点、直线、平面之间的位置关系以及相应的距离和夹角等问题.(3)把向量的运算结果“翻译”成相应的几何意义. 2.利用法向量求直线AB 与平面α所成的角θ的步骤 (1)求平面α的法向量n .(2)利用公式sin θ＝|cos 〈AB →，n 〉|＝|AB →·n ||AB →||n |，注意直线和平面所成角的取值范围为⎣⎢⎡⎦⎥⎤0，π2.3.利用法向量求二面角的余弦值的步骤 (1)求两平面的法向量.(2)求两法向量的夹角的余弦值.(3)由图判断所求的二面角是锐角、直角，还是钝角，从而下结论.在用法向量求二面角的大小时应注意：平面的法向量有两个相反的方向，取的方向不同求出来的角度当然就不同，所以最后还应该根据这个二面角的实际形态确定其大小.4.点面距的求解步骤(1)求出该平面的一个法向量.(2)找出从该点出发的平面的任一条斜线段对应的向量. (3)求出法向量与斜线段对应向量的数量积的绝对值，再除以法向量的模，即可求出点到平面的距离.1．若两异面直线l 1与l 2的方向向量分别为a ＝(0,4，－3)，b ＝(1,2,0)，则直线l 1与l 2的夹角的余弦值为( )A.32B.8525C.4315D.33答案 B解析 设l 1，l 2的夹角为θ，则cos θ＝|cos 〈a ，b 〉|＝0×1＋4×2＋－3×05×5＝8525.2．直角△ABC 的两条直角边BC ＝3，AC ＝4，PC ⊥平面ABC ，PC ＝95，则点P 到斜边AB 的距离是( )A ．5B ．3C ．3 2 D.125答案 B解析 以C 为坐标原点，CA ，CB ，CP 所在直线为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系．则A (4,0,0)，B (0,3,0)，P ⎝ ⎛⎭⎪⎫0，0，95，所以AB →＝(－4,3,0)，AP →＝⎝⎛⎭⎪⎫－4，0，95， 所以AP →在AB →上的投影长为|AP →·AB →||AB →|＝165，所以点P 到AB 的距离为d ＝|AP →|2－⎝ ⎛⎭⎪⎫1652＝16＋8125－25625＝3.故选B.3．把正方形ABCD 沿对角线AC 折起成直二面角，点E ，F 分别是AD ，BC 的中点，O 是正方形中心，则折起后，∠EOF 的大小为( )A ．(0°，90°)B ．90°C ．120°D ．(60°，120°)答案 C解析 OE →＝12(OA →＋OD →)，OF →＝12(OB →＋OC →)，∴OE →·OF →＝14(OA →·OB →＋OA →·OC →＋OD →·OB →＋OD →·OC →)＝－14|OA →|2.又|OE →|＝|OF →|＝22|OA →|，∴cos 〈OE →，OF →〉＝－14|OA →|212|OA →|2＝－12.∴∠EOF ＝120°.故选C. 4．平面α的法向量n 1＝(1,0，－1)，平面β的法向量n 2＝(0，－1,1)，则平面α与β所成二面角的大小为________．答案π3或2π3解析 设二面角的大小为θ，则cos 〈n 1，n 2〉＝1×0＋0×－1＋－1×12·2＝－12，所以cos θ＝12或－12，∴θ＝π3或2π3.5．如图，在长方体AC 1中，AB ＝BC ＝2，AA 1＝2，点E ，F 分别是平面A 1B 1C 1D 1、平面BCC 1B 1的中心．以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x ，y ，z 轴建立空间直角坐标系．试用向量方法解决下列问题：(1)求异面直线AF 和BE 所成的角；(2)求直线AF 和平面BEC 所成角的正弦值．解 (1)由题意得A (2,0,0)，F ⎝ ⎛⎭⎪⎪⎫1，2，22，B (2,2,0)，E (1，1，2)，C (0,2,0)．∴AF →＝⎝⎛⎭⎪⎪⎫－1，2，22，BE →＝(－1，－1，2)， ∴AF →·BE →＝1－2＋1＝0.∴直线AF 和BE 所成的角为90°.(2)设平面BEC 的法向量为n ＝(x ，y ，z )，又BC→＝(－2,0,0)，BE →＝(－1，－1，2)，则n ·BC →＝－2x ＝0，n ·BE →＝－x －y ＋2z ＝0，∴x ＝0，取z ＝1，则y ＝2，∴平面BEC 的一个法向量为n ＝(0，2，1)．∴cos 〈AF →，n 〉＝AF →·n|AF →||n |＝522222×3＝53333.设直线AF 和平面BEC 所成的角为θ，则sin θ＝53333，即直线AF 和平面BEC 所成角的正弦值为53333.。

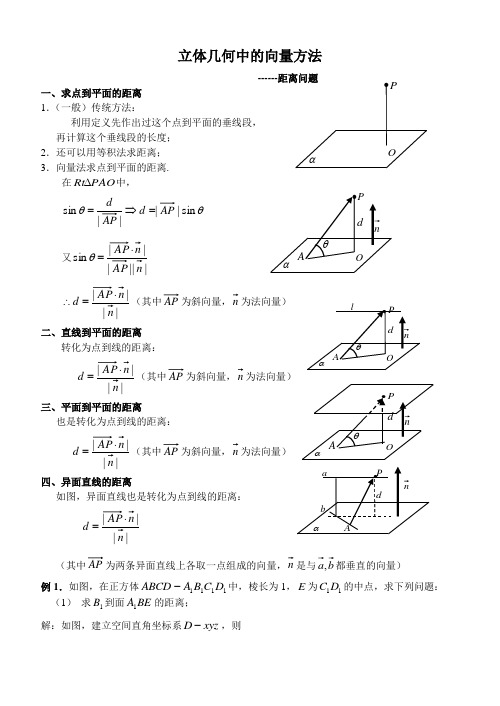
立体几何中的向量方法------距离问题一、求点到平面的距离 1．（一般）传统方法：利用定义先作出过这个点到平面的垂线段， 再计算这个垂线段的长度； 2．还可以用等积法求距离； 3．向量法求点到平面的距离.在PAO Rt ∆中，θθsin ||||sin AP d AP =⇒=又|||||sin n AP n AP =θ||n d =∴（其中AP 为斜向量，n 为法向量）二、直线到平面的距离 转化为点到线的距离：||n d =（其中AP 为斜向量，n 为法向量）三、平面到平面的距离也是转化为点到线的距离：||n d =AP 为斜向量，n 为法向量）四、异面直线的距离如图，异面直线也是转化为点到线的距离：||n d =（其中AP 为两条异面直线上各取一点组成的向量，n 是与b a ,都垂直的向量） 例1．如图，在正方体1111D C B A ABCD -中，棱长为1，E 为11D C 的中点，求下列问题： （1） 求1B 到面BE A 1的距离；解：如图，建立空间直角坐标系xyz D -，则•αOP),1,1,0(),0,21,1(11-=-=∴B A E A ，设),,(z y x n =为面BE A 1的法向量则⎪⎩⎪⎨⎧=-=+-⇒⎪⎩⎪⎨⎧=⋅=⋅0210011z y y x B A n E A n 取1=x ，得2,2==z y ，)2,2,1(=∴n选点1B 到面BE A 1的斜向量为)0,1,0(11=B A 得点1B 到面BE A 1的距离为32||11==n d （2）求C D 1到面BE A 1的距离；)2,2,1()1(:1=n BE A 的法向量知平面由解)0,0,1(11=A D 斜向量 311111==∴nn A D d BE A D 的距离为到面点 (3) 求面DB A 1与面11CB D 的距离；)1,1,1(:11-==AC n BD A 的法向量为由图知平面解)0,0,1(11=A D 又斜向量 311111==∴nn A D d BD A D 的距离为到面点 33111的距离为与即面CB D BD A (4) 求异面直线B D 1与E A 1的距离.xyz D -系如图建立空间直角坐标解:)1,1,1(),0,21,1(11-=-=∴B D E Axxxx111(0,0,1),(1,1,0),(1,0,1),(0,,1)2D B AE 则B D E A z y x n 11,),,(是与设=都垂直的向量，则⎩⎨⎧==⇒⎪⎩⎪⎨⎧=⋅=⋅x z x y B D n E A n 320011，取1=x ，得一个法向量为)3,2,1(=n 选11BD E A 与的两点向量)0,0,1(11=A D得11BD E A 与的距离为1414||11==n n A D d 练习1：1．如图在直三棱柱111C B A ABC -中，1==BC AC ,∠ACB 面BC A 1的距离.2．已知棱长为1的正方体1111D C B A ABCD -，求平面11C DA 和平面C AB 1间的距离3．已知棱长为1的正方体1111D C B A ABCD -，求直线1DA 和AC 间的距离。