惠州市2007届高三(文科)第一次调研考试

绝密★启用前试卷类型：A 2007年普通高等学校招生全国统一考试（广东卷）数学（文科）本试卷共4页，21小题，满分150分．考试用时l20分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．用2B铅笔将试卷类型（A）填涂在答题卡相应位置上．将条形码横贴在答题卡右上角“条形码粘贴处”．2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色宁迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用2B铅笔填涂选做题的题号（或题组号）对应的信息点，再作答．漏涂、错涂、多涂的，答案无效．5．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．参考公式：锥体的体积公式13V Sh =，其中S 是锥体的底面积，h 是锥体的高．如果事件A 、B 互斥，那么()()()P A B P A P B +=+．用最小二乘法求线性同归方程系数公式1221ˆˆˆ,ni ii nii x y nx ybay bx xnx==-==--∑∑ 一、选择题：本大题共l0小题，每小题5分，满分50分．在每小题给出的四个选项中．只有一项是符合题目要求的． 1．已知集合M ＝{x|10x +>}，N ＝{x|101x>-}，则M ∩N ＝ A ．{x|－1≤x ＜1} B ．{x|x ＞1} C ．{x |－1＜x ＜1} D ．{x |x ≥－1} 2．若复数(1)(2)bi i ++是纯虚数（i 是虚数单位，b 是实数），则b =A ．－2B ．12-C ．12D ．23．若函数3()f x x =（x R ∈），则函数()y f x =-在其定义域上是 A ．单调递减的偶函数 B ．单调递减的奇函数 C ．单凋递增的偶函数 D ．单涮递增的奇函数4．若向量a 、b 满足|a |＝|b |＝1，a 与b 的夹角为60︒，则a a ＋=a bA ．12 B ．32C ．1 D ．25．客车从甲地以60km ／h 的速度匀速行驶1小时到达乙地，在乙地停留了半小时，然后以80km ／h 的速度匀速行驶l 小时到达丙地．下列描述客车从甲地出发，经过乙地，最后到达 丙地所经过的路程s 与时间t 之间关系的图象中，正确的是6．若,,l m n 是互不相同的空间直线，,αβ是不重合的平面，则下列命题中为真命题的是A ．若//,,l n αβαβ⊂⊂，则//l nB ．若,l αβα⊥⊂，则l β⊥C ． 若,l n m n ⊥⊥，则//l mD ．若,//l l αβ⊥，则αβ⊥7．图l 是某县参加2007年高考的 学生身高条形统计图，从左到右 的各条形表示的学生人数依次记 为1A 、2A 、…、m A （如2A 表示身高（单位：cm ）在[150， 155）内的学生人数）．图2是统计图l 中身高在一定范围内学生人 数的一个算法流程图．现要统计 身高在160～180cm （含 160cm ，不含180cm ）的学生人数，那么在流程图中的判断框内应填写的条件是A ．9i <B ．8i <C ．7i <D ．6i <8．在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是 A ．310 B ．15 C ．110 D ．1129．已知简谐运动()2sin()()32f x x ππϕϕ=+<的图象经过点（0，1），则该简谐运动的最小正周期T 和初相ϕ分别为 A ．6,6T πϕ==B ．6,3T πϕ==C ．6,6T ππϕ==D ．6,3T ππϕ==10．图3是某汽车维修公司的维修点环形分布图公司在年初分配给A 、 B 、C 、D 四个维修点某种配件各50件．在使用前发现需将A 、B 、C 、D 四个维修点的这批配件分别调整为40、45、54、61件，但调整只能在 相邻维修点之间进行．那么要完成上述调整，最少的调动件次（n 件 配件从一个维修点调整到相邻维修点的调动件次为n ）为A ．18B ．17C ．16D ．15二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．11．在平面直角坐标系xoy 中，已知抛物线关于x 轴对称，顶点在原点O ，且过点P （2，4），则该抛物线的方程是 ．12．函数()ln (0)f x x x x =>的单调递增区间是 ．13．已知数列{n a }的前n 项和29n S n n =-，则其通项n a = ；若它的第k 项满足58k a <<，则k = ．14．（坐标系与参数方程选做题）在极坐标系中，直线l 的方程为sin 3ρθ=，则点(2,)6π到直线l 的距离为 ．15．（几何证明选讲选做题）如图4所示，圆O 的直径AB ＝6，C 为圆周 上一点，3BC =过C 作圆的切线l ，过A 作l 的垂线AD ，垂足为D ， 则∠DAC ＝ ．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分14分）已知ΔABC三个顶点的直角坐标分别为A （3，4）、B （0，0）、C （c ，0）．AB AC=，求c的值；（1）若0（2）若5c=，求sin∠A的值．17．（本小题满分12分）已知某几何体的俯视图是如图5所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形．（1）求该几何体的体积V；（2）求该几何体的侧面积S．18（本小题满分12分）下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据x3456y 2.534 4.5（1）请画出上表数据的散点图；（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程ˆˆ=+；y bx a（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性同归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? （参考数值：3 2.543546 4.566.5⨯+⨯+⨯+⨯=） 19（本小题满分14分）在平面直角坐标系xOy 中，已知圆心在第二象限、半径为2／2的圆C 与直线y x =相切于坐标原点O ．椭圆22219x y a +=与圆C 的一个交点到椭圆两焦点的距离之和为10．（1）求圆C 的方程；（2）试探究圆C 上是否存在异于原点的点Q ，使Q 到椭圆右焦点F 的距离等于线段OF 的长．若存在，请求出点Q 的坐标；若不存在，请说明理由． 20．（本小题满分14分）已知函数2()1f x x x =+-，α、β是方程()0f x =的两个根（αβ>），()f x '是()f x 的导数，设11a =，1()()n n n n f a a a f a +=-'，(1,2,)n =． （1）求α、β的值；（2）已知对任意的正整数n 有n a α>，记ln n n n a b a βα-=-，(1,2,)n =．求数列{n b }的前n 项和n S ．21．（本小题满分l4分）已知a 是实数，函数2()223f x ax x a =+--．如果函数()y f x =在区间[1,1]-上有零点， 求a 的取值范围．2007年普通高等学校全国招生统一考试 （广东卷）数学（文科）参考答案一、选择题二、填空题11．28y x = 12．1,e ⎡⎫+∞⎪⎢⎣⎭13． 2n －10；814．2 15．30三、解答题16．解：（1）()3,4AB =--，()3,4AC c =-- 由0AB AC =⇒()()()()33440c --+--=， 解得253c =．（2）当c ＝5时，2AC =，5cos 5AB AC A AB AC==， 进而sinA ＝552． 17． 解： （1）由题目知道该几何体是一个四棱锥其体积V ＝31SH ＝31⨯8⨯6⨯4＝64．（2）该几何体的四个侧面是两对全等的三角形其斜高分别为15h ==，2h == 故侧面面积S ＝5⨯8＋6⨯42＝40＋242．18．解：（1）如下图（2）y x ini i ∑=1＝3⨯2．5＋4⨯3＋5⨯4＋6⨯4．5＝66．5，x ＝46543+++＝4．5，y ＝2.534 4.54+++＝3．5，222221345686ni ix ==+++=∑，b ＝266.54 4.5 3.50.7864 4.5-⨯⨯=-⨯，a ＝3．5－0．7⨯4．5＝0．35．故线性回归方程为y ＝0．7x ＋0．35．（3）根据回归方程的预测，现在生产100吨产品消耗的标准煤的数量为0．7⨯100＋0．35＝70．35，故耗能减少了90－70．35＝19．65（吨）19． 解：（1）设圆心坐标为（m ，n ）（m <0，n >0），则该圆的方程为()()228x m y n -+-=．已知该圆与直线y ＝x 相切，那么圆心到该直线的距离等于圆的半径，则2n m -＝22．即n m -＝4， ① 又圆与直线切于原点，将点（0，0）代入，得m 2＋n 2＝8． ② 联立方程①和②组成方程组解得⎩⎨⎧=-=22n m ，故圆的方程为()()22228x y ++-=．（2）a ＝5，∴a 2＝25，则椭圆的方程为221259x y +=． 其焦距c ＝925-＝4，右焦点为（4，0），那么OF ＝4．要探求是否存在异于原点的点Q ，使得该点到右焦点F 的距离等于OF 的长度4，我们可以转化为探求以右焦点F 为顶点，半径为4的圆()2248x y -+=与（1）所求的圆的交点数．通过联立两圆的方程解得x ＝54，y ＝512． 即存在异于原点的点Q （54，512），使得该点到右焦点F 的距离等于OF 的长． 20．解：（1）解方程x 2＋x －1＝0得x ＝251±-， 由αβ>，知α=β=． （2）∵()21f x x '=+， ∴1()()n n n n f a a a f a +=-'2121n n a a +=+． ∵n a αβ>>（1,2,3,n =），且11a =， ∴b 1＝1ln -＝． ln n n n a b a βα-=-()()()()22222222121ln ln ln 2ln 2211n n n n n n n n n n n a a a a a b a a a a a βββββββααααααα---+---+-=====--+----+-， 即数列{b n }为首项为b 1，公比为2的等比数列．故数列{b n }前n 项和()()()1212212412n n n n b S +-==-⋅=--． 21．解：当a ＝0时，函数为()23f x x =-，其零点x ＝32不在区间[－1，1]上． 当a ≠0时，函数()f x 在区间[－1，1]分为两种情况：①方程()0f x =在区间[]1,1-上有重根．此时()4830a a ∆=++=，解得a =．当32a -=时，()0f x =的重根[]31,12x -=-． ②函数在区间[─1，1]上只有一个零点，但不是()0f x =的重根． 此时()()110f f -≤，即()()510a a --≤，解得15a ≤≤．③函数在区间[─1，1]上有两个零点，此时()()0,111,2110.a f f ⎧∆>⎪⎪-<-<⎨⎪⎪-≥⎩解得a <或5a ≥． 综上所述，如果函数在区间[─1，1]上有零点，那么实数a的取值范围为[)3,1,2⎛--∞+∞ ⎝⎦．。

惠州市高三毕业班第一次调研考试语文试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分。

共150分。

考试时刻150分钟。

注意事项：1．答第Ⅰ卷时，每小题选出答案后，用铅笔把第Ⅱ卷前面的单项选择题答题卷上对应题目的答案标号涂黑。

如需改动，用橡皮擦洁净后，再选涂其它答案。

不能答在试题卷上。

2．考生必须在第Ⅱ卷指定位置将学校、班级、姓名、学号填写清晰。

3．考试终止，上交第Ⅱ卷。

第Ⅰ卷（选择题共45分）一、（18分，每小题3分）1．下列词语中加点的字的读音，全都不相同的一组是A．客人恪守贿赂洛阳纸贵束之高阁B．剥削紧俏剑鞘霄壤之别硝烟充满C．园圃逮捕逋逃铺天盖地辅车相依D．纪录圮毁妃子讳疾忌医杞人忧天2．下列各组词语中，有错别字的一组是A．鱼船竭泽而渔直言仗义执言 B．鼓舞再接再厉提名金榜题名C．辐射幅员宽敞桃园世外桃源 D．废弛风驰电掣退化蜕化变质3．对下列词语意义的说明，正确的一组是A．棒喝（促人醒悟的警告）爱屋及乌（爱一个人连带爱他屋上乌鸦）不齿（不情愿提及）暴珍天物（损害灭绝天生的自然资源）B．齿冷（嘲笑）鞭辟入里（言辞或文章的道理专门深刻、透彻）赴敌（赶走敌人）别出心裁（另想出一种与众不同的新主意）C．腹议（预先构思文章）汗颜（因惭愧而出汗）耿耿于怀（怀着心事，专门不爽快）瓜田李下（容易引起嫌疑的地点）D．就范（听从支配和操纵）绝倒（形容大笑，前仰后合）分庭抗礼（分裂政权，对抗中央）黄花晚节（比喻人晚年能保持节操）4．下列各句中加点的成语的使用，恰当的一句是A．运算机是一种工具，尽管是高科技工具，拥有它并不意味着一切工作都能够事倍功半，一蹴而就。

B．他们疼爱自己的小孩，小孩也喜爱他们。

一家三口相濡以沫，美满幸福．C．天赋进展到七十分的，从古以来少有，进展到一百分的可能更是千载难逢。

D．有的部门或是人浮于事，或是在其位不谋其政，这些地点不减员、不裁官行不行？5．依次填入下列各句横线处的词语，最恰当的一组是真正重理的人，决不应轻文；__________，真正重文的人，也决不应轻理。

广东省惠州市2007届高三语文第一次模拟考试卷2007.4本试卷共四道大题，21小题，满分为150分。

考试时间150分钟。

一、语言文字运用（共24分）1.下列各组词语中，加点字的读音全都相同的一项是（3分）A.吁．请与．会驾驭．熨．帖鹬．蚌相争B.螃蟹．松懈．邂．逅押解．不屑．一顾C.山岫．乳臭．星宿．嗅．觉良莠．不齐D.憧．憬潼．关冲撞．瞳．仁灯影幢幢．．2.依次填入下列各句横线处的词语，最恰当的一项是（3分）（1）从整体上看，我国______事业的发展速度相当快，但西部地区的滞后状况也不容忽视。

（2）市场经济讲究诚信，公司对售出的商品，一定要按自己对该产品所制作的说明书承担责任，绝对不能______。

（3）艺术结构不可能信手拈来，＿＿＿，因为它是一种创造，是每一个作者必须认真探索的美学问题。

（4）并非说所有烦恼只需哈哈一笑便会＿＿＿，笑只不过是改变情绪的一种方法。

A.电信失言为所欲为涣然冰释B.电信食言随心所欲烟消云散C.电讯失言随心所欲涣然冰释D.电讯食言为所欲为烟消云散3.下列各句没有语病的一项是（3分）A.昨天，世界各大报纸关于伊拉克前总统萨达姆被绞死的事件都在显要位置作了详细的报道。

B.作为一个共产党员，想问题、办事情都要从党和人民的根本利益为出发点。

C.我和我学习成绩差不多的小玲都面临一个同样的问题，那就是如何在短期内提高自己的作文审题能力。

D.交响乐好听，但演出的票价昂贵，对月收入不丰的交响乐迷来说，大多数人难以承受数百元、上千元的票价。

4.请用一句话概括下列新闻的主要内容。

（不超过15个字）（5分）随着惠州经济的快速发展，越来越多的外国人来惠州工作、生活。

记者日前在惠州街头看到不少老外活跃的身影。

“这个能不能便宜点？”ISABELLA操着生硬的普通话与摊主讨价还价，最终以他满意的价格买下了一副春联。

这位德国小伙子告诉记者，这是他在中国过的第一个春节，他将按照中国的习俗度过这个有意义的春节。

广东省惠州市第一中学2006-2007学年度高三语文模拟考试卷2007.5一、（9分）1.下列词语中加点的字，读音全都正确的一组是(3分)A.马厩．（jiù）觊觎．（yú）戎马倥．（kōng）偬B.垂涎．（xián）投奔．（bēn）运筹帷幄．（wò）C.电荷．（hé）阔绰．（chuò）放荡不羁．（jī）D.斡．（wò）旋龃．（jǔ）龉醍．（tí）醐灌顶2．下列各句中加点的成语，使用正确的一项是(3分)A.在国有剧院团面临“经济效益”和“社会效益”双重危机的今天，门票价格却持续地水．涨船高．．．，普通百姓根本无力承受。

B.曾几何时，“北影”、“人艺”、“青艺”和“儿艺”等文艺团体的名声是何等响亮，每个金字招牌下面都藏龙卧虎，有诸多著名的艺术家、大明星和一长串赫赫有名的片名和剧目。

然而，这些都已经是明日黄花．．．．。

C.《满城尽带黄金甲》恢宏的场面和唯美的场景设计，15条琉璃瓦铺就的走廊构筑的皇宫内景、万朵菊花铺就的宫殿广场、强烈的颜色对比，给人以美轮美奂．．．．的感觉。

D. 联想集团以雄厚的科技实力和先进的经营理念为依托，亦步亦趋．．．．紧跟世界电子产业发展潮流，创下了骄人的业绩。

3．下列各句中没有语病的一句是（3分）A．今年1月，由卫生部主导制订的一份政府承担公共卫生及全民基本医疗、政府财政投入主导卫生事业为基本思路的医改新方案初稿，经媒体披露后引发来自各界的争论和质疑。

B.据美国国家地理网报道，就在不久前人们在东南亚水域新发现了一种美丽的观赏鱼物种，但由于世界范围的需求和过度的出口导致该物种在发现后不到几个月的时间就濒临灭绝。

C.安徽合力公司2006年叉车销售强劲，销售收入涨幅很有可能将超过40%以上。

公司预计2006年度实现净利润与上年相比增长50%。

D．海洋国家依赖对外贸易，国家安全范围不仅取决于主权所不及的海洋和贸易区域的秩序，还取决于本土治理。

广东省惠州市2007届高三第一次调研考试数学试题(理科卷)(2006.10)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题，共40分)一、选择题（每小题5分，共40分）1、化简=+-ii13 A ．i 21- B. i 21+ C. i +2 D. i -22、命题：“设b a bc ac R c b a >>∈则若22,,,”以及它的逆命题、否命题、逆否命题中，真命题的个数为 A ．0 B. 1 C. 2 D. 33、幂函数①1-=x y 及直线②x y =③1=y ④1=x将直角坐标系第一象限分成八个“卦限”Ⅲ，Ⅳ，Ⅴ，Ⅵ，Ⅶ，Ⅷ（如图所示），那么幂函 数23-=xy 的图象在第一象限中经过的“卦限”是A Ⅳ ⅦB Ⅳ ⅧC Ⅲ ⅧD Ⅲ Ⅶ4、某次考试，班长算出了全班40人数学成绩的 平均分为M ，如果把M N ，那么M ：N 为A 4140B 4041 C 2 D 15、函数),52sin(2)(ππ+=x x f 若对任意R x ∈，都有)()()(21x f x f x f ≤≤成立，则||21x x -的最小值为A 4B 2C 1D 216、等比数列{}n a 前n 项的积为T n ，若1863a a a 是一个确定的常数,那么数列25171310,,,T T T T ,中也是常数项的是A 10TB 13TC 17TD 25T7、从6人中选出4人分别到巴黎、伦敦、香港、莫斯科四个城市游览，要求每个城市有一人游览，每人只能游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有 A 240种 B 300种 C 144种 D 96种8、设奇函数]1,1[)(-在x f 上是增函数，且,1)1(-=-f 若函数12)(2+-≤at t x f 对所有的[]1,1-∈x 都成立，则当[]1,1-∈a 时，t 的取值范围是A 22≤≤-tB 202≥=-≤t t t 或或C 2121≤≤-t D 21021≥=-≤t t t 或或第Ⅱ卷(填空题、解答题共110分)二、填空题（每小题5分，共910、如图在边长为25cm 为23cm 是11.=-⎰dx x x )32(2212、我们知道：“过圆心为O 的圆外一点P 作它的两条切线 P A 、PB ，其中A 、B 为切点， 则POB POA ∠=∠.”这个性 质可以推广到所有圆锥曲线，请你写出其中一个： （注意：不要求证明结论的正确性）13．关于二项式2006)1(-x ,有下列三个命题：①该二项式展开式中非常数项的系数和是1-；②该二项式展开式中第10项是1996102006xC ；③当2006=x 时，2006)1(-x 除以2006的余数是1，其中正确的命题序号是 (把你认为正确的序号都填上) 14、（本小题有三个小题供选作，考生只能在①、②、③题中选做一题！多做不给分！） ①圆C ：{θθcos 1sin +==x y （θ为参数）的普通方程为 ，设O 为坐标原点，点M ),(00y x 在C 上运动，点P ),(y x 是线段OM 的中点，则点P 的轨迹方程为②、若BE 、CF 是△ABC 的高，且BCEF S S 四边形=ABC △，则A ∠= ③、已知,143,,=+∈b a R b a 则22b a +的最小值为 三、解答题（6个小题，共80分）15．（本题满分12分）已知πθπθ22,222tan <<-=.⑴求θtan 的值； ⑵求)4sin(21sin 2cos22πθθθ+--的值.16．（本题满分12分）月饼是一种时间性很强的商品，若在中秋节前出售，每盒月饼将获利5元，若到中秋节还没能及时售完，中秋节之后只能降价出售，每盒将亏损3元，根据市场调查，销量（百盒）的概率分布如下：. (1)设订购量为x 百盒时,获利额为y 元,下表表示与x 对应的y 的分布列，请在空格处填入适当的y 的值，并计算相应的获利期望值Ey ;第10题图17．（本题满分14分）已知等差数列{}n a 的前n 项和为n S ，21),(,133*=∈=b a N n S b n n 且，2153=+S S （1） 求数列{}n b 的通项公式； （2） 求证：221<+++n b b b18．（本题满分14分）如图，四面体ABCD 中，O 、E 分别是BD 、中点，2====BD CD CB CA ，2==AD AB .⑴求证：BCD AO 平面⊥⑵求异面直线CD AB 与所成角的余弦值； ⑶求点E 到平面ACD 的距离.19．（本题满分14分）如图过抛物线y x 42=的对称轴上任一点)(,0(m m p 作直线与抛物线交于A 、B 两点，点Q 是点P 关于原点的对称点.⑴设点P 满足),1,(-≠=λλλ为实数 证明：);(λ-⊥⑵设直线的方程是AB 0122=+-y x ， 过A 、B 两点的圆C 与抛物线在点A 处有共同的切线，求圆C 的方程.20.(本题满分14分)已知函数)(x f 的导数)(x f '满足1)(0<'<x f ，常数α为方程x x f =)(的实数根. ⑴若函数)(x f 的定义域为I ，对任意[][],,,,0b a x I b a ∈⊆存在使等式)()()()(0x f a b a f b f '-=-成立, 求证: 方程x x f =)(不存在异于a 的实数根⑵求证：当;)(,成立总有时x x f a x <>⑶对任意1x ，2x ，若满足2)()(,1,12121<-<-<-x f x f a x a x 求证EB惠州市2007届高三第一次调研考试 数学试题(理科卷)(2006.10) 参考答案9、729 10、62596 11、3412、过抛物线)0(22>=p py x 外一点P 作抛物线的两条切线PA 、PB （A 、B 为切点），若F 为抛物线的焦点，则PFB PFA ∠=∠（如果学生写出的是椭圆或双曲线，只要正确就给满分）13、①③14、①14)12(,1)1(2222=+-=+-y x y x ② 90° ③ 251三、解答题：（本大题共6小题，共80分） 15、(1)由22tan -=θ解得22tan -=θ或2tan =θ 3分 22tan ,2,22-=∴<<∴<<θπθππθπ 7分 (2)原式=223)22(1)22(1tan 1tan 1cos sin 1sin cos 1+=-+--=+-=+--+θθθθθθ 12分 16、（（2）由上表可见：预订400盒月饼时获利的数学期望Ey 最大，因此最合理17、(1)设等差数列{}n a 的公差为d ，由33332,21S a b a ==得 2分即d a d a 334211+=+，得d a =1 4分1:,21138,,211153===+=+d a d a S S 解得得又 6分所以)1(2,11+==-+=n n b n n a n n 8分(2))111(2)1(2+-=+=n n n n b n 10分得2)111(221<+-=+++n b b b n 14分18 (1)证明略 5分 (2) 异面直线CD AB 与所成角的余弦值为4211分 (3) 求点E 到平面ACD 的距离为72114分 19解：（1）直线AB 的斜率存在可设直线AB 的方程为m kx y +=代入抛物线并化简得0442=--m kx x 2分设A 、B 两点的坐标分别是A （),11y x ),(22y x B 则21,x x 是方程0442=--m kx x 的两根,所以m x x 421-= 3分由点P 满足),1,(-≠=λλλ为实数得2121,01x x x x -==++λλλ即点Q 是点P 关于原点的对称点,故点)2,0(),,0(m m Q =-从而的坐标是))1(,(),(),(21212211m y y x x m y x m y x λλλλλ-+--=+-+=-)(λ-⊥])1([221m y y m λλ-+-=])1(44[221222121m x x x x x x m ++⋅+=2212144)(2x mx x x x m +⋅+=0444)(2221=+-⋅+=x mm x x m 6分所以)(λ-⊥ 7分(2)由⎩⎨⎧==+-y x y x 401222得点A,B 的坐标分别是(6,9)、)4,4(- 由y x 42=得x y x y 21,412='=所以，抛物线在点A 处切线的斜率为3|6='=x y 9分设圆C 的方程是222)()(r b y a x =-+-则⎪⎩⎪⎨⎧-++=-+--=--2222)4()4()9()6(3169b a b a a b 11分 解得：223,23=-=b a 2125)4()4(222=-++=b a r 13分所以,圆C 的方程是2125)223()23(22=-++y x 14分 20、(1)用反证法，设方程x x f =)(有异于α的实根β,即αβββ>=不妨设,)(f ,则)()(αβαβf f -=-,在α与β之间必存在一点c ，αβ>>c由题意等式)()()()(c f f f '-=-=-αβαβαβ成立， 3分因为βα≠所以必有1)(='c f ，但这与1)(0<'<c f 矛盾因此，若β也是方程x x f =)(的根，则必有αβ=,即方程x x f =)(不存在异于α的实数根. 6分(2)令)()(x f x x h -= 7分0)(1)(>'-='x f x h )(x h ∴为增函数 8分又)(,0)(,,0)()(x f x x h x f a h >>>∴=-=即时当ααα 9分 (3)不妨设)()(,)(,1)(0,2121x f x f x f x f x x ≤∴<'<≤即为增函数 10分x x f x f -∴<-')(,01)(函数又 为减函数 11分12122211)()(0,)()(x x x f x f x x f x x f -≤-≤∴-≥-即 12分即2||||||.|||)()(|12121212<-+-≤--≤-ααx x x x x x x f x f ,2|)()(|21<-∴x f x f 14分。

广东省惠州市2024届高三第一次调研考试题语文试题及参考答案一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：“东南”与“西北”是古代中国频繁对举的两个方位概念。

司马迁说：“作事者必于东南，收功实者常于西北。

”这句话凝聚了古人丰富的地理经验。

很多历史文献也描述中国的地理大势为“天不足西北，地不满东南”。

不惟地形，“东南”与“西北”在经济、文化上也呈现出较大的地理差异。

西晋张华《博物志》记：“东南之人，食水之产；西北之人，食六畜产。

”欧阳修《论逐路取人札子》云：“东南之俗好文，故进士多而经学少；西北之人尚质，故进士少而经学多。

”两宋时期，在经济文化重心转移的大背景下，中国人口“东密西疏”的分布格局在南宋即已形成。

到了明代，郭之奇已使用“东南人满，西北土满”来形容这样的人口分布格局变化。

至清康熙时，移民殖边以均人口的思想也被人提出来，朱奇龄明确主张“以东南有余之民，任西北有余之地”。

进入近代，西北移民殖边之论成为潮流，“东南人满，西北土满”一语，为近代中国社会各界人士耳熟能详。

二十世纪二三十年代，“东南人满，西北土满”也早已是知识界表述中国人口分布的口头禅。

胡焕庸将半壁区划法具体落实在中国人口地理研究之中，创制出第一张中国人口密度图，提出了一条可以标识中国东西部人口差异的分界线——“胡焕庸线”（以下简称“胡线”），即“瑷珲—腾冲线”，因地名变迁也被称为“黑河—腾冲线”。

“胡线”是依靠较高精度的人口数据，运用分界线思维和标准化手段，在现代科学研究过程中化约和展现“东南人满，西北土满”传统认识的产物。

可以说，学理上的“胡线”提出不足百年，但事实上的“胡线”已存在了千余年。

不能忽视的另外一个事实是，“胡线”是建立在一个“整体的中国领土空间”基础上画出的人口地理分界。

近代中国的领土空间是随着清代疆域观念变化和国际条约体系的介入，以清代疆域为主体逐步确立下来的。

惠州市2007届高三模拟考试数学试题（文科卷）（2007.4）答案一．选择题(本大题共10小题，每小题5分，共50分)1．D 本题主要考察互为共轭复数的概念及复数的乘法运算．Z=1+1z i =+，1z i =-，2()2z i =-，故选 D ．2．C 本题主要考察含绝对值不等式的解法及集合间的运算交与补．集合P=}{2,1,0,1,2--，M=}{2,1，CuM ＝{}2,1≠≠∈x x z x 且，∴P ⋂CuM ＝}{0,1,2--．故选C ． 3．D 本题主要考察的是古典概型，一枚硬币连掷2次可能出现正正，反反，正反，反正四种情况，而只有一次出现正面的有两种，∴ P ＝42＝21 故选D ． 4．C 本题主要考察立体几种线线，线面的位置关系．A 是a//b 的充分条件B 是a//b 的充分必要条件，C 是a//b 的充分条件．D 是a//b 的必要不充分条件．故选C5．B 本题主要考察的是简单的线性规划问题．目标函数在点（2，4）处取得最大值20故选B6．B 本题主要考察数列由递推公式求通项或代入法求值．22(1)n n a n =-⇒394a =，52516a =，356116a a +=，故选B ．此题也可求2a ，3a ，4a ，5a ． 7．C 本题主要考察的是算法中条件分支问题，A 、B 、D 不含条件分支，解一元二次不等式要用到条件分支故选C ．8．B 本题主要考察向量的数量积及三角函数和值求角．由:a b ＝60cos ..-=θb a ⇒cos θ=21-， 故0120θ=，选B ．9．D 本题主要考察分式，绝对值不等式的解法．⎪⎩⎪⎨⎧≥->1122x x 或⎩⎨⎧≥-≤1432x x ⇒32≤<x 或1≤x 或235≤≤x ∴1≤x 或335≤≤x 选D ． 10．A 本题主要考察点与圆的位置关系及直线与圆的位置关系．点M 在圆内故22200x y a +<，圆心到直线的距离2d a =>．故直线与圆相离．选A ．二．填空题(本大题共4小题，每小题5分，共20分．)11．2π 本题主要考察正弦函数图像，相邻对称轴间的距离为半个周期，故此题关键是求函数的周期．T ＝22π=π． 12．45，35． 此题考察的是双曲线的基本概念．由于此题没有说明焦点的位置，因此要分类讨论．当焦点在x 轴时54e =；当焦点在y 轴时 53e =． 13．[0，1] 此题考察导数的应用以及解一元二次不等式．066)('2≤-=x x x f ⇒01x ≤≤． 14．4 考查直角三角形中的中线的性质及等腰三角形底边中线的性质．连接DE ，则DE=21AB=BE=DC ． ∴DG 平分EC ，故EG=4．15．（-3，6）或（5，-2）考查的是直线的参数方程问题．点(,)P x y 为直线上的点PA ==t =或t =-故P （-3，6）或（5，-2）．三．解答题（本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤）．16．（本小题满分12分）解．（1）由已知得．2221222b c a bc cos A bc bc +-===， …………………………………… (3分)又A ∠是△ABC 的内角，所以3A π∠=． …………………………………………… (6分)（2）（方法一）由正弦定理得．2bc a =， …………………………………………………… (7分)又 222b c a bc +=+，∴222b c bc +=， …………………………………………………………………… (9分) ∴ ()20b c -=，即 b c =． ……………………………………………………………… (10分)所以△ABC 是等边三角形． ………………………………………………………………… (12分)（方法二）()()12sin B sinC cos B C cos B C =-+--⎡⎤⎣⎦， ………………………………… (7分)又 ()12cos B C cos A +=-=-， ∴ ()311422cos B C ⎡⎤=----⎢⎥⎣⎦， ……………………………………………………… (8分)()1cos B C -=，又 ()B C ππ-∈-，， ……………………………………………………… (9分)∴ 0B C -=，即B C =， ……………………………………………………………… (10分)所以△ABC 是等边三角形． ……………………………………………………………… (12分)17．（本小题满分12分）解．(1) 422a a d =+，∴17924d d =+⇒=， ………………… (3分)2(2)94(2)41n a a n d n n =+-⋅=+-=+， ……………………… (6分)(2) ∵n n b a 2log =，∴4122n a n n b +==， ……………………… (9分) ∴63)12(3221])2(1[22224445149521-=--=+++=+++=+n n n n n b b b s ……… (12分) 18．（本小题满分14分） 解：(1)甲乙二人抽到的牌的所有情况(方片4用4 ’表示)为：（2，3）、（2，4）、（2，4 ’）、（3，2）、（3，4）、（3，4 ’）、（4，2）、（4，3）、（4，4 ’）、（ 4 ’，2）、（4 ’，3）（4 ’，4），共12种不同情况．……… (5分)(没有写全面时：只写出1个不给分，2—4个给1分，5—8个给2分，9—11个给3分)（2）甲抽到3，乙抽到的牌只能是2，4，4．因此乙抽到的牌的数字大于3的概率为32；…… (9分)（3）由甲抽到牌比乙大有（3，2）、（4，2）、（4，3）、（4 ’，2）、（4 ’，3）5种， ………… (11分) 甲胜的概率1512p =，乙获胜的概率为21712p =．∵125＜127，∴此游戏不公平．………… (14分)19．（本小题满分14分）证：(1) 连接AC 、OE ，AC BD=O ， ………… (1分)在△PAC 中，∵E 为PC 中点，O 为AC 中点．∴PA // EO ，…… (3分) 又∵EO ⊂平面EBD ，PA ⊄平面EBD ，∴PA //BDE ．………… (7分) （2）∵PO ⊥底面ABCD ，∴PO ⊥BD ． ………… (9分)又∵BD ⊥AC ，∴BD ⊥平面PAC ． ………… (12分)又BD ⊂平面BDE ，∴平面PAC ⊥平面BDE ． ………… (14分)P A BD OE C20．（本小题满分14分）解：（1）设椭圆方程为221(0,0,)mx ny m n m n +=>>≠且 ……………………… (2分)椭圆过M ，N 两点，∴32199212m n m n ⎧+=⎪⎪⎨⎪+=⎪⎩ ……………………… (3分) ⇒1914m n ⎧=⎪⎪⎨⎪=⎪⎩ ……………………… (4分) ∴椭圆方程为22194x y +=﹒故椭圆的离心率为3e =． ……………………… (6分) （2）设存在点P )(,x y 满足题设条件，∴2AP =()22x a y -+ 又22194x y += ∴2y =24(1)9x -， ∴2AP =()2x a -+24(1)9x -=22594()4(3)955x a a x -+-≤， ……………………… (8分) 当935a ≤即503a <≤时，2AP 的最小值为 2445a -依题意，24410,52a a ⎛5⎤-=⇒=±∉ ⎥3⎦⎝， ……………………… (10分) ∴935a >即533a <<，此时3x =， ……………………… (11分)2AP 的最小值为2(3)a -．依题意2(3)1a -=，∴2a =，此时点P 的坐标是)(3,0．……… (13分)故当2a =时，存在这样的点P 满足条件，P 点的坐标是)(3,0． ……………………… (14分)21．（本小题满分14分） 解：（1）()f x 与()g x 的图象关于1x =对称， 设点(,())M x f x 是()f x 上的任意一点．则点M 关于1x =的对称点(2,(2))x g x --在函数()g x 的图象上．∴()f x =(2)g x -3ax x =-+． ……………………… (2分)（2）'()f x =23a x -+，又1x =是函数()f x 的一个极值点，∴'(1)030f a =⇒-+=，得3a =， ……………………… (3分)故3(x)3f x x =-+．'2()333(1)(1)f x x x x =-+=-+-，当]1,1x ⎡∈-⎣，'()0f x ≤，∴()f x 在]1,1⎡-⎣上是减函数． ……………………… (4分)min ()(1)2f x f ==-，max (x)(1)2f f =-=， ……………………… (5分) 故对任意)(12,1,1x x ∈-，有12()()2(2)4f x f x -<--=． ……………………… (6分)（3）若()f x 在[1,)+∞是减函数，则'2(x)30f a x =-+<在[1,)+∞上恒成立．即23a x ≥在[1,)+∞上恒成立，此时a 不存在； ……………………… (8分) 若()f x 在[1,)+∞是增函数，即23a x ≤在[1,)+∞上恒成立．故3a ≤． …………… (10分)设00()1f x x >≥则[]00()()f f x f x >，∴00()x f x >矛盾， ……………………… (12分)若00()1x f x >≥则[]00()()f x f f x > ∴00()f x x >矛盾！ 故00()f x x =． ……………………… (14分)。

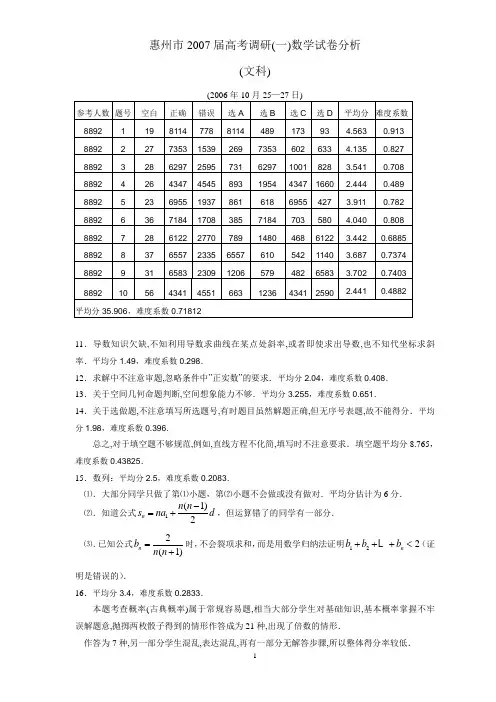
惠州市2007届高考调研(一)数学试卷分析(文科)11．导数知识欠缺,不知利用导数求曲线在某点处斜率,或者即使求出导数,也不知代坐标求斜率．平均分1.49，难度系数0.298．12．求解中不注意审题,忽略条件中”正实数”的要求．平均分2.04，难度系数0.408． 13．关于空间几何命题判断,空间想象能力不够．平均分3.255，难度系数0.651．14．关于选做题,不注意填写所选题号,有时题目虽然解题正确,但无序号表题,故不能得分．平均分1.98，难度系数0.396．总之,对于填空题不够规范,例如,直线方程不化简,填写时不注意要求．填空题平均分8.765，难度系数0.43825．15．数列：平均分2.5，难度系数0.2083．⑴．大部分同学只做了第⑴小题，第⑵小题不会做或没有做对．平均分估计为6分． ⑵．知道公式1(1)2n n n s na d -=+，但运算错了的同学有一部分． ⑶．已知公式2(1)n b n n =+时，不会裂项求和，而是用数学归纳法证明122n b b b +++<（证明是错误的）．16．平均分3.4，难度系数0.2833．本题考查概率(古典概率)属于常规容易题,相当大部分学生对基础知识,基本概率掌握不牢误解题意,抛掷两枚骰子得到的情形作答成为21种,出现了倍数的情形．作答为7种,另一部分学生混乱,表达混乱,再有一部分无解答步骤,所以整体得分率较低．17．(三角函数) 平均分5.7，难度系数0.4071．该题考查了三角函数的二倍角公式,正(余)弦函数的和(差)角公式的应用,特殊角的三角函数值,三角函数的周期性,以及简单的三角方程等知道,属中等偏易的基础题,特别是与向量的解决是本题的另一亮点．从学生答题抽样情况看,主要存在以下问题：⑴．对二倍角公式不熟悉,特别是二倍角公式的常用．⑵．对特殊角的三角函数值记忆不准确,如sin63ππ==．⑶．该题解题方法较多,特别是第(1)问：可化为cos cos )0x x x +=,同学们直接两边除以cos x 而无解,说明思维的严密性不够．⑷．个别学生对向量的垂直与平行的关系容易混淆,导致起步失分．⑸．对单调区间的求法,大多数同学是用整体代换的思想去求解,问题出现在不会解不等式,因此,同学们对于综合科知识还较欠缺．㈠．值得商榷的地方：文科学生,对形如sin(2)3x π+= ㈡．备考建议：①．加强基础知识的教学．②．关注学生的学习,找到适合学生的学习方法及教法,真正为学生服务,自己的教法尽量适合学生．③．注意学科知识内部的整合,特别是学科知识的交汇点处例题,将是高考命题的方向． 18题(立几) 平均分4.9，难度系数0.35．① 从试题本身而言,前两问相对而言比较基础简单,而第三问就感觉有点超出学生的能力范围,不常规．② 从得分情况来看,估计平均分大概在4—6分左右,大多数同学得分0分,只有少部分同学得满分．③ 从学生答题情况来看,主要存在以下几个问题：⑴很多学生都认为FM AD 或FM AB⑵不会做辅助线⑶知识点,概念,定理含糊不清， 在做第2问时,很多学生都是认为1FM BD ⊥,就可以推出11FM DD B ⊥面B ,有的同学干脆就是东拉西扯一点边都没沾上．在做第3问时,很多学生的答案是45°,但并不是题目所要求的二面角,学生几乎都把1BD 与平面ABCD 所成的线面角当成了二面角．⑷书写不规范,推理论证的依据不充分．⑸也有相当一部分学生采用向量法,但是建立不正确． ④ 答题方法而言有以下几种：(二面角) ⑴定义法 ⑵射影法 ⑶向量法⑤ 启示：要加强学生基础知识,要培养学生的空间感书写,论证更要加强,明确方法,尤其常用方法．19题分析：平均分3.3，难度系数0.275．本题考查三次函数,利用求导解决极值,单调性,方程根的问题,难度适当,学生解答情况,中等水平学生都能解决第1问的解,尖子生第二问基本能解决,得分率平均3分左右． 20题分析：平均分0.1，难度系数0.00715．该题为解析几何题，经批改后,总结如下：该题得分较低,分数得0—2分,小部分得7—9分,很少得满分． ①常见错误： 第一问：1．第一问没有使用A,B 为抛物线上的点推出12,,x x m σ与的关系,只用“AB PB λ=”推导证明．2．第1问中,由“AB PB λ=”推出“APPBλ=”对向量运算概念不清． 3． 第1问中,欲证“()QP QA QB λ⊥-”即证“()1QP QA OB λ⋅-=-”将“向量垂直的积为0”与“两直线垂直,斜率相乘为-1”混淆．4． 第一问中,对γ取特殊值,来证明．5． 第一问运算量较大,大部分学生运算过程混乱,或是为得出所需结论,跳过关键运算步骤．第一部错误暴露原因小结：运算能力的薄弱,对向量相关的基础知识点理解不清晰． 第二问：1． 受第一问运算的影响,第二问动笔的不多．2． 第二问分数只算出交点的坐标,但会有因y 将(4,4)-舍掉． 3． 第二问最多的错误是将AB 作为所求圆的直径来计算． 4． 第二问同样暴露了运算能力的问题． ② 其它解法问题：第一问： 211(,)4x A x 222(,)4x B x ，由1212()44x x AP PB x x m m λλλ-=⎧⎪=⇒⎨-=-⎪⎩ ② 2212(,()44x xQA QB x x m m λλλ-=-+-+ ③ 将②③结合得,12(,0)QA QB x x λλ-=-()0()QP QA QB QP QA QB λλ∴-=⇒⊥-第二问：① 求出切线斜率,结合A 点点坐标,求得过A 点与切线垂直的直线方程． ② 求出AB 的中垂线方程．结合①②求得交点即为所求圆的圆心, 即得圆的方程．总之:文科试题题型合理,知识覆盖率90%以上,试题很有梯度,区分度高,基础题占试卷的110左右,难度题为选择题第10题,5分,解答题第18题第3问,4分,第19题第2问,8分,第20题,14分．试题适合新课标要求．平均分59.2，难度系数0.395，试题偏难，调研二要吸取教训． 今后解题注意：① 计算量降低, ② 有关内容考查难度过大,如二面角计算,解析几何等． 学生解答情况见阅卷组的分析．惠州市2007届高考调研(一)数学试卷分析(理科)9．读程序,新增内容,对于条件的满足很多同学理解错误,导致答错．平均分3.4425，难度系数0.6885．10．关于几何概型问题,很多同学对于基本有利事件有误,或者计算出错,分数化小数取余出错．平均分3.985，难度系数0.797．11．关于定积分问题,部分学校未讲究选修,这部分内容未学,以致此题得分不高．平均分3.55，难度系数0.71．12．题目的理解不正确,很多读不懂题,得分率偏低．平均分0.565，难度系数0.113． 13．关于命题正确选择,答题不全面．平均分2.073，难度系数0.4145．14．此题为“三选一”,很多同学三题全做,结果后两题虽正确,但因为第一题错误不能得分,因此．此题丢分较亏．平均分2.455，难度系数0.491．总之，理科选择题得分大多的是10~~15分之间,失分较多． 理科15题：平均分9.2675，难度系数0.7723．本题考察三角函数的化简和求值,从试卷反映情况来看,,绝对部分学生对常用公式(两倍角的正切,余弦及和角公式)掌握得较好,大部分学生都注意了角的范围对函数的影响,知道应该取舍,出现的主要问题是学生运算能力差,有不少同学解错简单的方程及简单的乘除运算错,还有些化简的手法不太简明,总体来说,学生对这部分内容掌握得还好． 理科16题分析：平均分5.79，难度系数0.4825．本题考查概率知识,较好地体现了新课程的阅读理解能力的要求，但文字传述及图表冗长,学生对本类型题目缺乏心理素质来应对,大约13以上的学生全部空白,少数学生做得较好,但也存在表达不规范的问题,希望在以后的教学中加强学生对文字题的理解(应用题)的解题教学和应对心理训练及表达训练!理科17题：平均分5.145，难度系数0.3675．与文科15题基本类似．但理科前面比文科多了一些运算要求：求1,a d ，所以有少数同学算不出1,a d ．建议：在提倡简便方法解数列问题的同时，要加强计算1,a d 的基本方法（解方程组）的训练． 18题 (立几)评价：平均分9.1175，难度系数0.65125．一. 试题情况：试题不错,是一道比较常规的题目,能够考察学生空间概念及数量关系,立体几何的几个重要方法都可在题目中体现,题目难度也适中． 二. 学生答题情况：① 第一问答对的可能是3成左右,大部分同学推理不严密,不知道用勾股定理,还有约2成的同学默认,AO BCD ⊥平面而建立空间直角坐标系．② 第二问做到cos cos 44OBM OBM ∠=∠=的约有65﹪,但能得出正确结果的约45﹪．③ 第3问做对的约3成,很多同学建立坐标用法向量,但是或是坐标写错或算错数,方法很多同学都会,但得到正确结果的没有一半． 三. 启示：① 明确方法：立几是难度不太的题,只要明确几类常用方法,一般的学生都能做． ② 加强运算的准确性,要是算错数了,得分会很低． 19题答题分析：平均分1.365，难度系数0.0975．该题为解析几何题,经批改后,总结如下：① 该题得分较低,分数得0—2分,小部分得7—9分,很少得满分．② 常见错误：第一问： 1． 第一问没有使用A,B 为抛物线上的点推出12,,x x m σ与的关系,只用“AB PB λ=” 推导证明．2． 第1问中,由“AB PB λ=”推出“APPBλ=”对向量运算概念不清． 3． 第1问中,欲证“()QP QA QB λ⊥-”即证“()1QP QA OB λ⋅-=-”将“向量垂直的积为0”与“两直线垂直,斜率相乘为-1”混淆．4． 第一问中,对γ取特殊值,来证明．5． 第一问运算量较大,大部分学生运算过程混乱,或是为得出所需结论,跳过关键运算步骤．第一部错误暴露原因小结：运算能力的薄弱,对向量相关的基础知识点理解不清晰．第二问： 1． 受第一问运算的影响,第二问动笔的不多．2． 第二问分数只算出交点的坐标,但会有因y 将(4,4)-舍掉． 3． 第二问最多的错误是将AB 作为所求圆的直径来计算． 4． 第二问同样暴露了运算能力的问题． ③ 其它解法问题：第一问： 211(,)4x A x 222(,)4x B x ，由1212()44x x x x m m AP PB λλλ-=-=-⎧=⇒⎨⎩ ②2212(,()44x xQA QB x x m m λλλ-=-+-+ ③ 将②③结合得,12(,0)QA QB x x λλ-=-()0()QP QA QB QP QA QB λλ∴-=⇒⊥-第二问：③ 求出切线斜率,结合A 点点坐标,求得过A 点与切线垂直的直线方程． ④ 求出AB 的中垂线方程．结合①②求得交点即为所求圆的圆心, 即得圆的方程． 理科20题试题分析：平均分0.185，难度系数0.0132． 本题得分率较低,主要原因有以下几点：① 前19题的计算量较大,大部分学生没有时间做20题．② 20题第一问需用反证法,虽然一部分学生知道用反证法,但相当一部分学生不知道反证法的步骤,证明过程不够严谨,传述不规范．③20题第二问需要对所证不等式变形,考察相应函数的单调性,同时需用到导数的性质,但学生在这方面的能力较弱．④20题第二问主要考察导数,函数与不等式的综合应用,能力要求较高．总之：数学理科试卷，有不少题具有新意，个别题目是原创题．有一定的梯度和区分度．由于第一轮复习没有结束，各学校复习进度也不一样，很自然较难考出好成绩．平均分65.7，难度系数0.438，试题偏难，调研二要吸取教训．各分数段分析：可以看出：要提高理科数学平均成绩必须抓好41~66分这一群体学生的成绩，要提高文科数学平均成绩必须抓好30~84分这一群体学生的成绩，怎么抓?首先，我们要分析文、理科学生数学能力的差异；其次，我们要研究对策．文、理科学生数学能力的差异是显著的．在数学上，理科学生更善于反思，能主动寻找新旧知识的联系，通过新知识的学习深化对旧知识的理解，从而有意识地整合知识，提高解题的能力，增强学好数学的自信心，激发内心对数学美的欣赏，进一步提高数学成绩来证实自己的能力，形成良好的循环．而文科学生缺乏反思的意识，不能行之有效地自我控制学习的内容，不会主动寻找已学的有关知识来理解新内容、解决新问题，更缺乏对数学美的欣赏．思维方式的差异：文理学生在对待同一问题时，由于他们所持的态度和采取的行为方式有较大的差异，文科学生更倾向于借助形象思维分析问题，理科学生更倾向于进行抽象思维的逻辑思考，理科学生观察数学问题常常是全方位和多角度的，文科学生往往是局部、孤立的．理科学生往往能够通过多个不同角度对题中的数、形、结构等方面的特征进行审查和对比联想，并尝试移植方法，使问题熟悉化、简单化，而文科学生往往只停留在“认知”阶段，或虽有深入，但也不善于分解转化问题．理科中的优秀学生观察事物经常具有“动中窥静，静中思动”的良好观察品质，他们能利用运动和静止的辨证关系来观察、分析和处理数学问题，使解题左右逢源，得心应手，游刃有余．数学思维能力的差异：在数学抽象概括能力方面，文理科学生有较大的差异，理科学生在收集数学材料所提供的信息时，能迅速地完成抽象概括的任务，同时具有概括的欲望，乐意地、积极主动地进行概括工作，文科学生的概括能力较差，积极性也不高，在数学推理能力方面，理科学生在逻辑推理方面有较大的优势，而文科学生更乐于直觉推理．在选择判断能力方面，理科学生在判断选择中较少受表面非本质因素的干扰，判断的准确率较高，判断迅速，对做出的判断具有清晰的认识，能区分逻辑判断和直觉猜测，他们具有明显的追求最合理的解法，探究最清晰、最简单同时也是最“优美”的解法的心理倾向；而文科学生则更注重的题型的记忆．在数学探索能力方面，理科学生表现出来的灵活性，对数学问题的监控能力及思维过程中的自我意识，提出问题，大胆猜测等能力，都明显地好于文科学生．造成这些差异的原因是多方面的，这里不一一分析．有什么对策呢？1．序渐进，加强学法指导：①．帮助学生提高听课效率：做到精力高度集中②．做好复习和总结：③．科学训练：2．正视差异，因材施教：3．要重视“读（阅读、理解）、写（书写表达）、算（心算、口算、数字计算、字母运算）、记（记忆）、练（规范练习）”能力的提高．我们在课堂教学的过程中，要时刻关注培养学生什么能力？通过什么途径来培养这些能力？教学语言要注意些什么？怎样通过语言的表现力、感染力来凝聚学生的思维能力？谢谢大家！。

惠州市高三第一次调研考试数 学（文科）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。

2．回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号，写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分。

在每个小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知{1,2,4,8,16}A =，2{|log ,}B y y x x A ==∈，则AB =（ ） （A ）{1,2}（B ）{2,4,8}（C ）{1,2,4}（D ）{1,2,4,8}（2）若复数z 满足(12)(1)i z i +=-，则||z =（ ）（A ）25 （B ）35（C ）5 （D （3）若11tan ,tan()32ααβ=+=,则tan =β（ ）（A ） 17 （B ） 16 （C ） 57 （D ） 56（4）函数,y x x px x R =+∈（ ）（A ）是偶函数 （B ）是奇函数 （C ）不具有奇偶性 （D ）奇偶性与p 有关（5）若向量(1,2)a x =+和向量(1,1)b =-平行，则a b +＝（ ）（A （B （C （D ）2（6）等比数列{}n a 的各项为正数，且564718a a a a +=，则3132310log log log a a a +++=（ ）（A ）12 （B ）10 （C ）8 （D ）32log 5+ （7）命题“任意[]21,2,0x x a ∈-≤”为真命题的一个充分不必要条件是（ ）（A ）4a ≥ （B ）4a ≤ （C ）5a ≥ （D ）5a ≤（8） 已知036020x y x y x y -≥⎧⎪--≤⎨⎪+-≥⎩，则22x yz +=的最小值是（ ）（A ）1 （B ）16 （C ）8 （D ）4（9）执行如图所示的程序框图，则输出S 的值为（ ）（A ）2 （B ）3-（C ）12-（D ）13（10）某几何体的三视图如右图，其正视图中的曲线部分为半圆，则该几何体的表面积为（ ）（A ）2(19)cm π+ （B ）2(224)cm π+ （C）2(104)cm π++（D）2(134)cm π+ （11）已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2,2,AB SA SB SC ====则三棱锥的外接球的球心到平面ABC 的距离是（ ）（A（B ）1 （C（D（12）双曲线M ：22221(0,0)x y a b a b-=>>的实轴的两个端点为A 、B ，点P 为双曲线M 上除A 、B 外的一个动点，若动点Q 满足,QA PA QB PB ⊥⊥,则动点Q 的轨迹为（ ）（A ）圆 （B ）椭圆 （C ） 双曲线 （D ）抛物线第Ⅱ卷本卷包括必考题和选考题两部分。

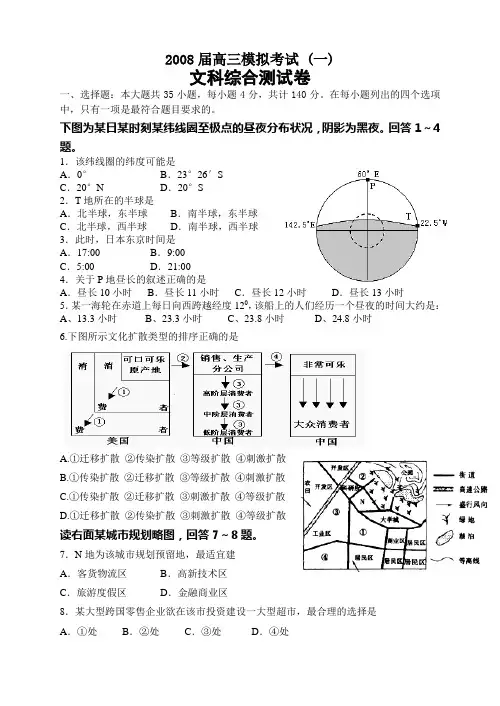
2008届高三模拟考试 (一)文科综合测试卷一、选择题：本大题共35小题，每小题4分，共计140分。

在每小题列出的四个选项中，只有一项是最符合题目要求的。

下图为某日某时刻某纬线圈至极点的昼夜分布状况，阴影为黑夜。

回答1～4题。

1．该纬线圈的纬度可能是A．0°B．23°26′SC．20°N D．20°S2．T地所在的半球是A．北半球，东半球B．南半球，东半球C．北半球，西半球D．南半球，西半球3．此时，日本东京时间是A．17:00 B．9:00C．5:00 D．21:004．关于P地昼长的叙述正确的是A．昼长10小时B．昼长11小时C．昼长12小时D．昼长13小时5．某一海轮在赤道上每日向西跨越经度120，该船上的人们经历一个昼夜的时间大约是：A、13.3小时B、23.3小时C、23.8小时D、24.8小时6.下图所示文化扩散类型的排序正确的是A.①迁移扩散②传染扩散③等级扩散④刺激扩散B.①传染扩散②迁移扩散③等级扩散④刺激扩散C.①传染扩散②迁移扩散③刺激扩散④等级扩散D.①迁移扩散②传染扩散③刺激扩散④等级扩散读右面某城市规划略图，回答7～8题。

7．N地为该城市规划预留地，最适宜建A．客货物流区B．高新技术区C．旅游度假区D．金融商业区8．某大型跨国零售企业欲在该市投资建设一大型超市，最合理的选择是A．①处B．②处C．③处D．④处读世界某大洲区域图，回答9～11题。

9．E为某种气候类型，它沿此大洲西海岸延伸2100千米，其沿海岸线延伸的原因和气候类型名称分别是A．地形；热带沙漠气候B．降水；热带草原气候C．大气环流；热带草原气候D．洋流；热带沙漠气候10．F自然带在此处分布的最高纬度低于35°，其主要的影响因素和自然带名称分别是A．陆地的纬度分布；亚热带常绿硬叶林B．降水条件；热带荒漠带C．地形；热带荒漠带D．洋流；亚热带常绿硬叶林11．M地为世界重要的渔场，其主要成因是A．温带海区B．暖寒流交汇C．上升流的影响D．河流的流入中国古代文明博大精深，在物质文明和精神文明方面均成就斐然。

惠州市2007届高三第一次调研考试英语试题(2006．10)(本试题共四部分，满分150分)第一部分：听力(共两节，满分32．5分)做题时，先将答案划在试卷上。

录音内容结束后，你将有两分钟的时间将第一节的答案转涂到答题卡上和将第二节的答案填人答题卷标号为16—20的空格中。

第一节：听对话或独自(共15小题；每小题1．5分，满分22．5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独自前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第1段材料，回答第1—3题。

1. Where does the conversation take place?2. What will the man have for the meal?3. How much will they each pay for the meal?听第2段材料，回答第4—6题。

4. Where does this conversation take place?A. Over the phone.B. In the street.C. At home.5. When will the man come to the woman's house?A. On Saturday morning.B. On Saturday evening.C. On Sunday.6. What can the man not resist?A. Lunch.B. Chocolate and tea.C. Cakes.听第3段材料，回答第7—9题。

7. What is the woman going to do at the very beginning of the conversation?A. To watch TV.B. To go out.C. To do some reading.8. What does the man like doing?A. Going out.B. Watching TV.C. Doing some reading.9. What do they probably do at last?A. Watch TV together.B. Go out and enjoy themselves together.C. Do their music.听第4段材料，回答第10—12题。

文数惠州市届高三第一次调研考试惠州市2012届高三第一次调研考试数学试题（文科）本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

参考公式：锥体的体积公式：Sh V 31 （S 是锥体的底面积，h 是锥体的高）第I 卷 选择题（共50分）一、选择题（本大题共10小题，每小题5分，满分50分．每小题给出的四个选项中，只有一项是符合题目要求．）1．已知全集U={1，2，3，4},集合A={1,3，4}，B={2，3}，则图中阴影 部分表示的集合为( ) A ．{2} B.{3} C.{1,4}D.{1,2,3,4}2．复数i i+-11的值是( ) A.1 B.-1 C.iD. -i3．已知向量)4,(),2,1(x b a ==，，若向量⊥，则x=( )A.2B.-2C.8D.-84．从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如 右图）。

由图中数据可知身高在[120，130]内的学生人数为( )A.20B.25C.30D.355．设{a n }是等差数列，且a 2+a 3+a 4=15，则这个数列的前5项和S 5=( )A.10B.15C.20D.256．右图是底面半径为1，母线长均为2的圆锥和圆柱的组合体，则该组合体的侧视图的面积为( )A.8πB.6πC.34+D.32+7.函数1)4cos()4sin(2)(-+-=x x x f ππ，x∈R 是( ) A ．最小正周期为2π的奇函数B ．最小正周期为π的奇函数C ．最小正周期为2π的偶函数D ．最小正周期为π的偶函数8．设平面区域D 是由双曲线1422=-x y 的两条渐近线和抛物线y 2=-8x 的准线所围成的三角形（含边界与内部）．若点(x ，y)∈D，则目标函数z=x+y 的最大值为( ) A.-1 B.0 C.1D.39.“lgx，lgy ，lgz 成等差数列”是“y 2=xz”成立的( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分也不必要条件10.规定记号“⊗”表示一种运算，即2b a ab b a ++=⊗（a,b 为正实数），若31=⊗k ，的，只记第一题的分。

2007届惠州市高三第一次政治调研测试题一、单项选择题（在每题给出的四个选项中，只有一项是最符合题意的。

本大题共24小题。

每小题2分，共48分。

）1．党中央、国务院从我国经济社会发展全局出发做出重要战略部署，决定推进开发，这对于提升京津冀乃至渤海弯地区的国际竞争力，形成东中西互动，优势互补，共同发展，区域协调发展格局具有重要意义。

A．天津滨海新区 B．厦门经济开发区C．环渤海经济开发区 D．辽宁经济开发区2．6月10日是中国的第一个“”，主题是保护文化遗产，守护精神家园。

A．物质文化遗产日 B．文化遗产日C．非物质文化遗产日 D．精神文化遗产日3．国务院办公厅转发了建设部等九部门《关于调整稳定的意见》。

A．经济适用房经济适用房供应结构B．经济适用房供应结构经济适用房价格C．住房供应结构住房价格D．住房价格住房供应结构4．十届全国人大常委会第二十二次会议表决通过了《中华人民共和国刑法正案（六）》和修订后的：A．《中华人民共和国义务教育法》 B．《反垄断法》C．《农民专业合作经济组织法》 D．《刑事诉讼法》5．2006年4月22日，博鳌亚洲论坛2006年年会开幕，本届年会的主题是：A．亚洲寻求共赢，亚洲的新机会 B．亚洲新的机会，共创世界美好未来C．亚洲的新机会，建设和谐世界 D．共同发展、共同繁荣6．5月9日，第60届大选产生首届人权理事会，中国以146票当选为：A．常务理事 B．理事会成员C．理事国理事 D．理事成员7．“八荣八耻”就是坚持以热爱祖国为荣、以危害祖国为耻，以服务人民为荣、以背离人民为耻，以崇尚科学为荣、以愚昧无知为耻，以辛勤劳动为荣、以好逸恶劳为耻，以团结互助为荣、以损人利己为耻，以诚实守信为荣、以见利忘义为耻，以遵纪守法为荣、以违法乱纪为耻，以艰苦奋斗为荣、以骄奢淫逸为耻。

树立社会主义荣辱观：①是改造世界观、人生观、价值观的正确取向②具有民族性、时代性，充分体现了社会主义先进文化基本要求③体现了社会主义价值观的鲜明导向，赋予青少年新的有感染里的人生信条④传承了中华文化，吸引了外来思想文化，发展了中国社会主义道德规范体系A．①② B．①②③ C．①②④ D．①②③④费涅克是一名美国商人，旅游时瀑布的水声激发了他的灵感。

惠州市2007届高三（理科）第一次调研考试数 学 试 题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟第Ⅰ卷（选择题，共40分）一．选择题（每小题5分，共40分） 1．化简31ii-=+( ) A ．12i - B ．12i + C ．2i + D ．2i -2．命题：“设a 、b 、c R ∈，若22ac bc >则a b >”以及它的逆命题、否命题、逆否命题中，真命题的个数为（ ）A ．0B ．1C ．2D ．3 3．幂函数①1y x -=,②y x =及直线③1y =， ④1x =将直角坐标系第一象限分成八个“卦 限”：Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ，Ⅶ，Ⅷ（如 图所示），那么幂函数32y x-=的图象在第一象限中经过的“卦限”是（ ）A ．Ⅳ，ⅦB ． Ⅳ，ⅧＣ．Ⅲ，Ⅷ D ． Ⅲ，Ⅶ 4．某次考试，班长算出了全班40人数学成绩的平均分为M ，如果把M 当成一个同学的成绩与原来的40个分数一起，算出这41个分数平均值为N ，那么:M N 为（ ）A ．4041 Ｂ．4140Ｃ．2 Ｄ．1 5．函数)52sin(2)(ππ+=x x f ，若对任意x R ∈，都有12()()()f x f x f x ≤≤成立，则12x x -的最大值为（ ）A ．4B ．2C ．1D ．216．等比数列{}n a 前n 项的积为n T ，若3618a a a 是一个确定的常数，那么数列10T ，13T ，17T ，25T 中也是常数的项是（ ）A ． 10TB ． 13TC ．17TD ． 25T7．从6人中选出4人分别到巴黎、伦敦、香港、莫斯科四个城市游览，要求每个城市有一人游览，每人只能游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有（ ） A ．240种 Ｂ．300种 Ｃ．144种 Ｄ．96种 8．设奇函数()f x 在[1,1]-上是增函数，且(1)1f -=-．若函数，2()21f x t at ≤-+对所有的[1,1]x ∈- 都成立，则当[1,1]a ∈-时，t 的取值范围是（ ）x11-A ．22t -≤≤B ． 2t ≤-或0t =或2t ≥C ．1122t -≤≤D ．12t ≤-或0t =或12t ≥第Ⅱ卷（填空题、解答题 共110分）二．填空题(每小题5分，共30分)9．阅读下列程序框图，该程序输出的结果是 ．10．如图，在边长为25cm 的正方形中截去直 角边长为23cm 的两个等腰直角三角形，现有 均匀的粒子散落在正方形中，粒子落在中间带 形区域的概率是 ． 11．222()3x x dx -=⎰ ． 12．我们知道：“过圆为O 的圆外一点P 作它的两条切线PA 、PB ， 其中A 、B 为切点，则POA POB ∠=∠．”这个性质可以推广到所有圆锥曲线，请你写出其中一个：． 13．关于二项式2006(1)x -，有下列三个命题：①．该二项式展开式中非常数项的系数和是1-；②．该二项式展开式中第10项是1019962006C x；③．当2006x =时，2006(1)x -除以2006的余数是1．其中正确命题的序号是 （把你认为正确的序号都填上）． 14．（本小题有三个题供选作，考生只能在①、②、③题中选做一题！多做不给分！) ①．圆C ：x y =+=⎧⎨⎩1cos sin θθ，，（θ为参数）的普通方程为 ，设O 为坐标原点，点00()M x y ，在C 上运动，点()P x y ，是线段OM 的中点，则点P 的轨迹方程为 ．②．若BE 、CF 是ABC ∆的高，且ABC BCEF S S ∆=四边形，则A ∠= ． ③．已知,a b R ∈，341a b +=，则22a b +的最小值为 ． 三．解答题（6个小题，共80分）15．（本题满分12分）已知πθπθ22,222tan <<-=．⑴求θtan 的值；⑵求⎪⎭⎫ ⎝⎛+--4sin 21sin 2cos 22πθθθ的值．第10题图16．（本题满分12分）月饼是一种时间性很强的商品，若在中秋节前出售，每盒将获利5元，若到中秋节还没能及时售完，中秋节之后只能降价出售，每盒将亏损3元．根据市场调查，销量n （百盒）的概⑴．设订购量为x 百盒时，获利额为y 元．下表表示与x 对应的y 的分布列，请在空格处填入适当的y 值，并计算相应的获利期望值Ey ；（解答本题第⑴小题只需在下面的表格的空位中填入你认为正确的数据即可） 解：⑴．⑵．17．（本题满分14分）已知等差数列{}n a 的前项和为n s ，1n n b s =，且3312a b =，3521s s +=． ⑴．求数列{}n b 的通项公式；⑵．求证：122 nb b b+++<．18．（本小题满分14分）如图，四面体ABCD中，O、E分别是BD、BC的中点，2,CA CB CD BD AB AD======⑴．求证：AO⊥平面BCD；⑵．求异面直线AB与CD所成角余弦的大小；⑶．求点E到平面ACD的距离．C E19．（本题满分14分）如图,过抛物线24x y =的对称轴上任 一点(0,)(0)P m m >作直线与抛物线交于A 、B 两点，点Q 是点P 关于原点的对称点．⑴．设点P 满足AP PB λ=（λ为实数）， 证明：()QP QA QB λ⊥-；⑵．设直线AB 的方程是2120x y -+=，过A 、B 两点 的圆C 与抛物线在点A 处有共同的切线，求圆C 的方程．20．（本题满分14分）已知函数()f x 的导数()f x '满足0()1f x '<<，常数α为方程()f x x =的实数根． ⑴．若函数()f x 的定义域为I ，对任意[,]a b I ⊆，存在0[,]x a b ∈，使等式()()f b f a -=0()()b a f x '-成立，求证：方程()f x x =不存在异于α的实数根； ⑵．求证：当x α>时，总有()f x x <成立；⑶．对任意12,x x ，若满足12||1,||1x x αα-<-<，求证12|()()|2f x f x -<．惠州市2007届高三第一次调研考试数学（理科）参考答案9．39729=10．62596 11．4312．①过抛物线22x py =（0p >）外一点P 作抛物线的两条切线PA 、PB （A 、B 为切点），若F 为抛物线的焦点，则PFA PFB ∠=∠．（如果学生写出的是抛物线的其它方程，只要正确就给满分）②过椭圆22221x y a b+=（0a b >>）外一点P 作椭圆的两条切线PA 、PB （A 、B 为切点），若F为椭圆的一个焦点，则PFA PFB ∠=∠．（如果学生写出的是椭圆的其它方程，只要正确就给满分）③过双曲线22221x y a b-=（0,0a b >>）外（两支之间）一点P （P 不在渐近线上）作双曲线的两条切线PA 、PB （A 、B 为切点），设F 为双曲线的一个焦点．⑴若A 、B 在同一支，则PFA PFB ∠=∠；⑵若A 、B 不在同一支，则PF 平分AFB ∠的邻补角．（如果学生写出的是双曲线的其它方程，只要正确就给满分） 13．①、③14．①(-+=x y 1122)、22(21)41x y -+=， ②090， ③125； 15．⑴．由222tan -=θ，解得22tan -=θ或θtan =2． ………………………………… 3分 ∵22πθπ<<, ∴2πθπ<<, ∴22tan -=θ． ……………………………………… 7分 ⑵．原式=θθθθθθπθθθtan 1tan 1cos sin sin cos 4sin 21sin cos 1+-=+-=⎪⎭⎫ ⎝⎛+--+, ………………………………… 10分 ∴原式=223221221+=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛--. ……………………………………………………… 12分16．⑴．(评分说明：每填正确一个数据给2分，共10分)⑵．由上表可见：预订400盒月饼时获利的数学期望Ey 最大，因此最合理．…………………… 12分 17．⑴．设等差数列{}n a 的公差为d ，由3312a b =，得332a s =， ……………………………… 2分 即112433a d a d +=+，得1a d =， …………………………………………………………… 4分 又3521s s +=，得181321a d +=，解得：11a d ==， ……………………………………… 6分 所以11n a n n =+-=，2(1)n b n n =+． ………………………………………………………… 8分⑵．由2112()(1)1n b n n n n ==-++， ………………………………………………………… 10分得：121111112[(1)()()]2(1)222311n b b b n n n +++=-+-++-=-<++． ……………… 14分 18 方法一：⑴．证明：连结OC ,,.BO DO AB AD AO BD ==∴⊥ ………… 1分 ,BO DO BC CD ==，CO BD ⊥． ……… 2分在AOC ∆中，由已知可得1,AO CO ==… 3分而2AC =， 222,AO CO AC ∴+= ………………… 4分 90,o AOC ∴∠=即.AO OC ⊥ ………………… 5分,BD OC O =∴AO ⊥平面BCD ． …………………………… 6分 ⑵．解：取AC 的中点M ，连结OM 、ME 、OE ，由E 为 BC 的中点知ME ∥AB,OE ∥DC ，∴ 直线OE 与EM 所成的锐角就是异面直线AB 与CD 所成的角，………………………………8分 在OME ∆中，111,22EM AB OE DC ==== OM 是直角AOC ∆斜边AC 上的中线，∴112OM AC == ……………………………… 9分 ∴222cos 2OE EM OM OEM OE EM +-∠==⋅⋅， ………………………………………………… 10分CE∴异面直线AB 与CD所成角余弦的大小为4． …………………………………………………… 11分 ⑶．解：设点E 到平面ACD 的距离为h ． E ACD A CDE V V --=，1133ACD CDE h S AO S ∆∆∴⋅=⋅⋅ ………………………………………………12分在ACD ∆中，2,CA CD AD ===122ACD S ∆∴==,而1AO =，2122CDE S ∆==∴172CDEACDAO S h S ∆∆⨯⋅===，∴点E 到平面ACD的距离为7………………………………………………………… 14分 方法二：⑴．同方法一．⑵．解：以O 为原点，如图建立空间直角坐标系，则(1,0,0),(1,0,0),B D -1(0,0,1),((1,0,1),(1,2C A E BA CD =-=-2cos ,BA CD BA CD BA CD⋅∴<>==⋅…………… 9分 ∴ 异面直线AB 与CD ．……⑶．解：设平面ACD 的法向量为(,,),n x y z =则(,,)(1,0,1)0(,,)1)0n AD x y z n AC x y z ⎧⋅=⋅--=⎪⎨⋅=⋅-=⎪⎩， ∴0x z z +=⎧⎪-=，令1,y =得(3,1,n =-是平面ACD 的一个法向量．又1(,,0),22EC =-∴点E 到平面ACD 的距离 37EC n h n⋅===．……………………………………… 14分 19．解⑴．依题意,可设直线AB 的方程为m kx y +=,代入抛物线方程y x 42=，得：2440x k x m --= ① …………………………………………………………… ２分设A 、B 两点的坐标分别是11(,)x y 、22(,)x y ，则12,x x 是方程①的两根，所以，124x x m =-． ……………………………………………………………………… ３分 由点P 满足AP PB λ=（λ为实数，1λ≠-），得0121=++λλx x ， 即12x x λ=-． 又点Q 是点P 关于原点的以称点，故点Q 的坐标是(0,)m -，从而(0,2)QP m =．1122(,)(,)QA QB x y m x y m λλ-⋅=+-+1212(,(1)).x x y y m λλλ=--+-12()2[(1)]QP QA QB m y y m λλλ⋅-=-+- =])1(44[221222121m x x x x x x m ++⋅+ =2212144)(2x m x x x x m +⋅+ =221444)(2x m m x x m +-⋅+ =0 (6)所以，()QP QA QB λ⊥-． ………………………………………………………………… 7分 ⑵．由221204x y x y ⎧-+=⎨=⎩得点A 、B 的坐标分别是(6,9)、(4,4)-． 由y x 42=得241x y =，1,2y x '= 所以，抛物线y x 42=在点A 处切线的斜率为63x y ='=． …………………………………… 9分设圆C 的方程是222)()(r b y a x =-+-， 则22229163(6)(9)(4)(4)b a a b a b -⎧=-⎪-⎨⎪-+-=++-⎩……………………………………… 11分 解得：222323125,,(4)(4)222a b r a b =-==++-=．……………………………………… 13分 所以，圆C 的方程是2125)223()23(22=-++y x ． ……………………………………… 14分 20．⑴．用反证法， 设方程()f x x =有异于α的实根β，即()f ββ=，不妨设βα>，则()()f f βαβα-=-，在α与β之间必存在一点c ，c αβ<<，由题意使等式()()()()f f f c βαβαβα'-=-=-成立， …………………………………… 2分 因为αβ≠，所以必有()1f c '=，但这与0()1f x '<<矛盾．因此，如若β也是方程()f x x =的根，则必有βα=，即方程()f x x =不存在异于α的实数根．… 4分 ⑵．令()()h x x f x =-， ………………………………………………………………………… 5分 ()1()0h x f x ''=->， …………………………………………………………………………… 6分 ()h x ∴为增函数． ………………………………………………………………………………… 7分 又()()0,h f ααα=-=∴当x α>时，()0h x >，即().x f x > ………………………………… 9分 ⑶．不妨设12x x ≤，0()1,()f x f x '<<∴为增函数，即12()().f x f x ≤ …………………… 10分 又()10,f x '-<∴函数()f x x -为减函数． ……………………………………………………… 11分 即11222121()(),0()().f x x f x x f x f x x x -≥-∴≤-≤- ………………………………………… 12分 即21212121|()()|||.||||||2,f x f x x x x x x x αα-≤--≤-+-<∴12|()()|2f x f x -<． …………………………………………………………………………… 14分。

高三第一次模考质量分析本次市一模统考与一个月前进行的考试比较，出现了新的变化，暴露出了一些新的问题。

总体来讲，与兄弟学校相比，我们学校的成绩有较大的差距。

这说明，我们本次一模考试没有达到我们预期的目标，可以说考得很不理想。

我们只有本着一种实事求是的态度对本次考试情况作全面深入的分析，找出隐藏在现象背后的、导致考试退步的真正原因，然后对症下药，采取有针对性的措施，才能够化劣势为优势，才能够转危为安，才能够在来年的六月份有一份好的心情。

因此，前一阶段，我们分别召开了高三年级管理委员会会议，分析和部署了近期的工作任务，以备课组为单位分别召开了学科研讨会，制定了下阶段的复习计划和思路，校长还组织召开了部分学生座谈会，进行了问卷调查，也对学生进行了个别访谈，掌握了大量的第一手材料。

我们已基本形成了二模复习的总体思路。

等一下校长会在这方面进行重点说明。

下面我结合本次考试情况以及上午区教研室会议精神，对本次考试以及二模复习谈一点意见和看法。

一、目前存在的突出问题：1、语数外三门总分达线人数严重不足。

2、两门选测科目达到2B的人数数量不足，质量也不高。

3、三门总分上线学生与选测2B达标学生吻合度不高，错位严重。

特别是270——295之间的学生与2B的交集数量很少。

从学生个体来讲，尹巧313、周健309、鲍莉305、姚菁302等4位同学没达到2B；280——300之间有31人语数外三门总分没有达300分。

施洪俊2A+、张宏强1A1A+、毛晓青1A1B、杨健、殷婷各有2A等同学选测科目都很优秀，但三门总分离300分还差几分。

班主任和任科老师要对每个学生进行分析。

4、数学这一薄弱科目没有得到加强，在难度加大的情况下整体水平下降，严重影响一模达线人数。

就拿6班和7班来举例：6班300以上6名，300分以上7个。

7班与以往相比，正常情况下至少还需要上5个以上。

假如排除语文和英语其他因素，只要数学一门各提高5分，就有5名同学上300分，并且选测在2B上。