马斯京根法总结
- 格式:pdf
- 大小:339.53 KB
- 文档页数:4

第五章 河道洪水演算及实时洪水预报河道洪水演算,是以河槽洪水波运动理论为基础,由河段上游断面的水位、流量过程预报下游断面的水位、流量过程。
本文着重介绍马斯京根洪水演算方法以及简化的水力学方法。
5.1 马斯京根演算法马斯京根演算法是美国麦卡锡(G . T. McCarthy)于1938年在美国马斯京根河上使用的流量演算方法。
经过几十年的应用和发展,已形成了许多不同的应用形式。
下面介绍主要的演算形式。
该法将河段水流圣维南方程组中的连续方程简化为水量平衡方程,把动力方程简化为马斯京根法的河槽蓄泄方程,对简化的方程组联解,得到演算方程。
5.1.1 基本原理该法的基本原理,就是根据入流和起始条件,通过逐时段求解河段的水量平衡方程和槽泄方程,计算出流过程。
在无区间入流情况下,河段某一时段的水量平衡方程为122121)(21)(21W W t O O t I I -=∆+-∆+ (5-1) 式中:1I 、2I 分别为时段初、末的河段入流量;1O 、2O 分别为时段初、末的河段出流量;1W 、2W 分别为时段初、末的河段蓄量。
河段蓄水量与泄流量关系的蓄泄方程,一般可概括为)(O f W = (5-2)式中:O 为河段任一流量O 对应的槽蓄量。
根据建立蓄泄方程的方法不同,流量演算法可分为马斯京根法、特征河长发等。
马斯京根法就是按照马斯京根蓄泄方程建立的流量演算方法。
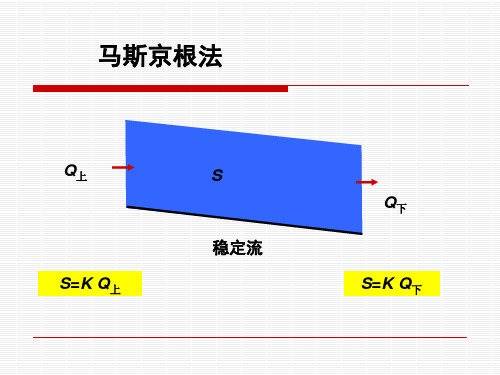
5.1.2 马斯京根流量演算方程马斯京根蓄泄方程可写为Q K O x xI K W '=-+=])1([ (5-3)式中:K 为蓄量参数,也是稳定流情况下的河段传播时间;x 称为流量比重因子;Q '为示储流量。
联立求解式(5-2)和(5-3),得到马斯京根流量演算公式为1211202O C I C I C O ++= (5-4)其中:⎪⎪⎪⎩⎪⎪⎪⎨⎧∆+-∆--=∆+-+∆=∆+--∆=t Kx K t Kx K C t Kx K Kx t C t Kx K Kx t C 5.05.05.05.05.05.0210 (5-5) 1210=++C C C (5-6)式中:0C 、1C 和2C 为马斯京根洪水演算方法的演算系数,,都是K 、x 和t ∆的函数。

马斯京根法的文献综述马斯京根法(Marshakian法)是古地磁学中一种地磁地层学方法,广泛应用于地磁地层学的研究中。
本文将围绕马斯京根法对地磁地层学的应用展开文献综述,总结出该方法的原理、应用领域及发展现状。
马斯京根法的原理主要基于地球磁场的变化和地壳运动之间的关系。
通过对地层剖面中的磁化属性进行测量,并和古地磁数据进行比较,可以推测地壳的水平移动和地磁场的变化。
马斯京根法的核心思想是将地壳运动和地球磁场的变化联系起来,从而揭示地层剖面中不同地层之间的相对年代差异。
马斯京根法最早是由俄罗斯地球物理学家M.M.Marshak于1930年提出,用于分析地球磁场的历史变化和地壳构造的演化。
随着研究的深入,马斯京根法的应用范围也逐渐扩大到了不同地球科学领域,如古地磁学、古地磁年代学、地球演化等。
在古地磁学中,马斯京根法是一种重要的研究方法。
通过测量剖面中不同岩石的自诱磁化强度和地磁比例系数(K值),可以计算出相对磁化强度和地磁矩系数(q值),进而推测岩石颗粒的尺寸和岩石的磁化历史。
这些数据对于研究地球磁场的变化和地壳运动的速度提供了重要的线索。
在古地磁年代学中,马斯京根法可以用于确定地层的准确年代。
通过比较不同剖面中的磁化特征和古地磁脉冲,可以建立起地层剖面之间的年代关系,并推断出地层的相对年代。
通过与有年代的化石资料结合,还可以进一步确定地层的绝对年代。
在地球演化研究中,马斯京根法可以揭示地壳运动和地球磁场的演化过程。
通过对不同断裂带地磁特征的测量和比较,可以推测断裂带的活动时间和断裂的位移速度。
这些数据可以用于研究地壳运动的规律和地球磁场的变化。
马斯京根法是一种重要的地磁地层学方法,对于研究地球磁场的变化和地壳运动的演化具有重要的意义。
但是由于该方法的测量精度和理论基础的限制,目前仍然存在一定的局限性。
未来需要进一步深入研究,提高方法的可靠性和适用性,推动马斯京根法在地球科学领域的进一步发展和应用。


马斯京根法的文献综述马斯京根法(Maslach Burnout Inventory,MBI)是一个用于测量工作倦怠(burnout)的常用工具。
工作倦怠是指个体因长期在工作中承受巨大压力而产生的一种负面情绪和心理状态。
马斯京根法最早由美国心理学家克里斯蒂娜·马斯京根(Christina Maslach)和苏珊·杰克逊(Susan E. Jackson)于1979年设计开发,至今已成为评估工作倦怠程度的金标准之一。
本文将综述马斯京根法的基本结构、应用范围、研究进展以及对工作倦怠的影响和应对措施等方面的文献,以期为相关研究和实践提供参考。
一、马斯京根法的基本结构马斯京根法是一个由22个项目组成的标准问卷,用于测量工作倦怠的三个维度:情感耗竭(Emotional Exhaustion,EE)、个人成就感(Personal Accomplishment,PA)和脱离工作(Depersonalization,DP)。
情感耗竭是指个体感到精疲力尽、失去动力和情绪极度疲惫;个人成就感是指个体对自己在工作中所取得的成就和效能感的评价;脱离工作是指个体对工作和工作对象产生冷漠、疏远和消极态度的现象。
通过对这三个维度的测量,可以全面了解个体在工作中的倦怠程度,为进一步干预提供依据。
二、马斯京根法的应用范围马斯京根法最初是为了评估医护人员的工作倦怠而设计的,但随着研究的不断深入,它已经被广泛应用于各个领域和职业。
不论是医疗卫生、教育、服务行业,还是工商企业、政府机构,甚至是军队和体育界,都可以使用马斯京根法来测量工作倦怠,了解员工的心理状态,优化组织管理,改善工作环境。
马斯京根法也被用于研究工作倦怠与工作绩效、员工流失、组织效力等之间的关系,为实际操作提供科学依据。
三、马斯京根法的研究进展自问卷设计以来,马斯京根法已经被翻译成多种语言,并在全球范围内得到广泛应用。
许多研究者通过对马斯京根法的运用和检验,不断对其进行修订和完善,以适应不同文化、职业和群体的特点。

马斯京根法——河道洪水演算的线性有限差解洪水模拟是水文学中一个重要的研究方向,它可以使用洪水模拟软件模拟河流洪水流动的过程。
它可以模拟河流的洪水流动的特征,如洪水体面、流速等。
马斯京根法是用于求解河流洪水的一种数值模拟技术,它的精度高,算法复杂度低,是目前广泛应用的数值模拟技术。
马斯京根(MUSLE)法是用于求解河流洪水的线性有限差分技术,它的精度高,算法复杂度低,因此在求解洪水演算时具有良好的精度和高效率。
它利用一维椭圆型线性有限差分法,由一维椭圆型线性有限差分方程式组成。
马斯京根法包括两个重要的部分:一是运用有限差分的椭圆型公式构建数学模型,以描述河流洪水的水动力特性;二是由于有限差分法提出的几何特性限制,采用线性变换方法来解决这一特性,求得洪水体面曲线。
由于马斯京根方法是一种精确的线性有限差分技术,它可以较好地模拟河流洪水的水动力特性,可以反映洪水体面曲线和洪水流速变化等重要信息。
它具有计算精度高、算法复杂度低、分析时间短等优点,已在洪水模拟中得到广泛的应用。
马斯京根法在河流洪水演算中的应用越来越广泛,它可以解决多维洪水模拟中存在的洪水体面分析、洪水流量分析等复杂问题。
此外,它还可以用于许多水文学研究中,如洪水潮汐研究、河流断面几何形状研究等。
综上所述,马斯京根法是一种精确的线性有限差分技术,可以解决洪水模拟中的复杂问题,可以反映洪水体面曲线和洪水流速变化等重要信息,用于洪水模拟的应用越来越广泛。
由于其精度高、算法复杂度低、计算精度高等特点,因此马斯京根法是河道洪水演算中非常有价值的研究方法。
马斯京根法的文献综述马斯京根法是一种基于两个星子资料(Star Data)集合进行关联的方法,主要应用于生物信息学、医学、社会学、经济学等领域。
它是由荷兰数学家马斯京根于1986年提出,目前已成为数据分析和知识发现的常用工具。
本文将对马斯京根法的发展历程、原理及应用进行综述,以期为相关领域的研究者提供参考。
一、马斯京根法的发展历程马斯京根法最初是由马斯京根在研究神经网络时提出的。
他首先提出了一种将两个不同的星子资料(Star Data)集合进行关联的数学方法,该方法通过对两个不同的星子资料(Star Data)集合的数学综合,来发现两个星子资料之间的复杂关联。
随后,马斯京根法被应用到生物信息学、医学、社会学、经济学等领域,以发现不同领域数据之间的关联关系,促进相关领域的研究和发展。
二、马斯京根法的原理马斯京根法的原理主要是基于数学统计学的方法,通过对两个不同的星子资料(Star Data)集合进行关联分析,发现两个星子资料之间的关联关系。
其数学原理涉及到线性代数、概率论、信息论等多个数学领域的知识。
在具体的实施过程中,马斯京根法主要包括如下几个步骤:1)收集两个不同的星子资料集合;2)对两个星子资料集合进行预处理,包括数据清洗、数据转换等操作;3)通过数学方法对两个星子资料集合进行综合分析,发现两者之间的相关性;4)利用统计学方法对所得结果进行检验,确定其显著性。
三、马斯京根法的应用马斯京根法在多个领域得到了广泛的应用。
在生物信息学领域,研究人员利用马斯京根法来分析基因表达数据,发现不同基因之间的关联关系,从而揭示基因调控网络的结构和功能。
在医学领域,马斯京根法被应用于疾病诊断和预后预测,通过对临床数据和分子生物学数据的关联分析,提高疾病诊断和治疗的准确性。
在社会学和经济学领域,马斯京根法被用来分析不同指标之间的关联关系,揭示社会和经济现象的内在规律。
四、马斯京根法的局限性尽管马斯京根法在数据关联分析方面表现出了良好的效果,但也存在一些局限性。
马斯京根法的文献综述马斯金根法(Maslach Burnout Inventory)是一种用于测量工作倦怠的问卷。
它由克里斯蒂娜·马斯金和她的同事三木德美编制并于1981年发表。
马斯金根法通过对工作者的情感、情绪和认知三个方面进行评估,帮助人们了解自己的工作倦怠程度。
该问卷被广泛应用于临床、教育、研究和管理领域,成为了研究工作倦怠的主要量表之一。
马斯金根法将工作倦怠分为三个维度:情感耗竭、个人成就感和脱离感。
情感耗竭指个体对工作的失望和疲惫,个人成就感指对自己工作的不满意度和无效感,脱离感则指对工作的疏远和冷漠。
通过对这三个维度的测量,可以全面了解个体的工作倦怠状况,有助于及时发现和解决问题。
对于临床实践来说,马斯金根法在心理健康评估中起到了至关重要的作用。
通过该问卷,医生和心理咨询师可以更好地了解患者的心理状态,帮助他们更好地调整工作和生活的平衡。
教育领域也可以利用马斯金根法对教师和学生的工作倦怠进行评估,帮助他们避免过度的学习压力和工作压力。
在研究领域,马斯金根法的应用为关于工作倦怠和心理健康的研究提供了重要的数据支持,为深入了解这一领域提供了基础。
在管理领域,马斯金根法也被广泛应用于组织行为和人力资源管理中。
通过该问卷,管理者可以更好地了解员工的工作倦怠状况,及时发现问题并采取措施加以解决。
这对于提高员工的工作热情和工作效率具有重要的意义。
不过,也有人对马斯金根法提出了一些质疑。
有学者认为,该问卷可能受到了文化和社会背景的影响,因此不同地区和不同群体的应用效果可能会有所不同。
一些研究也发现,情感耗竭这一维度在不同行业和不同职业中的表现可能会有所差异,因此需要根据具体情况进行灵活应用。
马斯京根法洪水演算总结
河道洪水演算的方法很多,主要分为两类,一是以圣维南方程组为基础的水力学方法;另一类是以水量平衡方程和槽蓄方程为基础的水文学方法。
水力学方法物理意义明确,但是需要详细的河道形态、糙率、比降资料。
水文学方法重点考虑水文要素之间的联系,能很好模拟洪水在河道内的主要特征,简单实用,可操作性强。
水文学的河道洪水演进方法主要有:马斯京根法、线性回归法、汇流系数法、特征河长法、滞后演算法等,其中以马斯京根法应用最为广泛。
马斯京根法计算简单、快捷,对河道地形和糙率资料要求低,在一般的河道洪水演算中效果较好。
马斯京根法可分为线性和非线性两类,求解的参数估计方法包括试算法、最小二乘法、矩法、最小面积法和遗传算法等。
1.线性回归法
基于水文学方法和线性汇流叠加原理,建立了河段下断面某日演算流量与上断面多日流量的相关关系:
1
,1,1,11()n
S S S S S S S S t i t i t
t t i Q Q L W R α++++-==--+∑ (1) 11n i i α
==∑ (2)
式中:t S Q 为s 断面t 时段断面平均流量3/m s ;i=0,1,…,n 为系数个数;i
α为线性组合系数;,1t S S L +为河段损失流量3/m s ;,1t
S S W +为河段区间饮水流量3/m s ;,1t S S R +为河段区间加水流量3/m s 。
上述枯水流量演算方程的实质是建立河段下断面流量与上断面若干历史时刻流量以及河段引水、损失等因子间的多元线性关系,系数i α反映了对枯水流量演进规律的定量描述,式(2)为河段水量平衡约束方程。
线性回归法的基本原理是在保证河段水量平衡的条件下,建立演算河段下断面出流与上断面各日入流过程的相关关系。
通过优化,能充分反映河段演进规律的演算系数。
2.汇流系数法
汇流系数法的实质是基于马斯京根线性运动波方程,根据上断面的入流过程(上边界条件)和T=0时刻的流量沿程分布(初始条件),通过连续应用运动波演算方程推求下断面的出流过程。
对于任何一个复杂的入流过程,可以用单位脉冲序列和延迟单位脉冲序列进行离散化表达。
由于线性差分方程满足叠加原理,任何一个复杂的入流序列所形成的出流序列都可借助于单位脉冲序列和汇流系数进行计算,因此只要求得连续演算情况下的汇流系数,应用运动波演算法即可推求下断面出流过程。
汇流系数法将演算河段等分为n 个子河段,假定每个子河段的马斯京根参数一致,用马斯京根法连续进行n 次演算,得到河段下断面出流过程。
汇流系数法缩小了演算河段长度和演算时段,从而接近马斯京根流量演算法的基本假定,演算效果有所改善。
3.马斯京根法
3.1线性马斯京根法
天然河道中洪水波的演进与变形可用圣维南方程组表示,以槽蓄方程代替复杂的动力学方程、以水量平衡方程代替连续方程。
马斯京根法将槽蓄量看作由柱蓄和楔蓄组成,在波前阶段,楔蓄量为正值,在波后阶段,楔蓄量为负值。
用河段上、下两个断面的流量作参数,假定天然河道中的断面流量与相应的槽蓄量近似具有单值关系,建立蓄量方程:
'[(1)]W K xI x Q Q =+- (3)
2021121Q C I C I C Q =++ (4) 00.50.5t Kx C t K Kx ∆-=∆+- 10.50.5t Kx C t K Kx ∆+=∆+- 20.50.5t Kx Kx C t K Kx
-∆+-=∆+- (5) 012=1C C C ++ (6)
式中,0C 、1C 、2C 均为流量演算系数;1I 、2I 分别为计算时段始末的河段入流量3/m s ;1Q 、2Q 分别为计算时段始末的河段出流量;K 为蓄量常数;X 为流量比重因数;t 为计算时段长。
马斯金根法假定K 和x 都是常数,这就要'Q 和槽蓄量W 成单一线性系,只有在此槽蓄量下的'Q 值等于该蓄量所对应的恒定流流量0Q 时才能满足这一要求,即'Q =0Q ,这就是'Q 的物理意义。
而K 值是槽蓄曲线的坡度,K 值等于在相应蓄量W 下恒定流状态的河段传播时间,x 值为流量比重系数,与河道、洪水各个参数有关,随着河道洪水参数的变化而变化。
对于K 、X 参数的确定,一般采用人工试算法,通过假定不同的X 值,点绘W~'Q 的关系曲线,其中能使二者关系成为单一曲线的值即为所求x 值。
但是在实际操作中,有些河段用试错法求K 、X 值经常会遇到不论x 取任何值,W~'Q 关系呈现8字型,而不是单一直线;有些河段W~'Q 关系虽然呈现线性关系,但是为不规则曲线。
而且不一定能找出最优参数使计算的流量和实测流量的拟合误差最小。
此外,操作者的主观经验也会明显影响参数值。
3.2分段马斯京根法
为了保证连续方程上、下端面流量在计算时段内呈现线性变化,槽蓄方程任何时刻流量在河段内呈线性变化,参数K 、X 为常量及流量在计算时段内和沿程变化呈直线分布。
分段法把推求河段按需要分成若干段,使计算时段与各段洪水波传播时间接近,即满足t K 。
因为马斯京根法的基本假定是河段入流和出流在计算时段内沿河长呈直线变化,当演算河段长度为该河段特征河长时,马斯京根法演算效果才好。
实际操作中常取K/Δt 为整数,用以分河段进行马斯京根连续演算。
3.3变参数马斯京根法
同一条河道的马斯京根参数不是唯一的,而是随着不同场次洪水的洪峰流量、流速、洪水总量等诸多因素动态变化,马斯京根模型参数不应只采用一场洪水或多场洪水估计的平均值,而是应该实行参数的实时动态估计。
由于河道
水力特性的非线性,不同量级的洪水传播时间和洪峰流量的衰减程度不一样。
通过实测资料率定洪峰流量与参数K、X之间的关系,计算时根据上游站的洪峰流量选用本次洪水的参数。
变参数法实质上还是对每次洪水进行线性处理,不同洪水选取不同参数。
通过对塔里木河1997-2010年间洪水的推演,按照洪峰流量将参数分级归类,可以发现参数K随着流量的增加有减小的趋势,符合客观规律。
3.3分层马斯京根法
根据河道断面特性,把入流量分层处理,相应各层仍按照线性方法推流公式计算,但各层参数取值不同,下端面出流为各层总和。
分层方法处理了河道参数非线性问题,特别适合复式河道。
4.对区间来(引)水的处理
马斯京根法是基于水量平衡原理上建立的,但是对于某些河流,上下游站水量差异极大。
所以用此方法进行河道洪水演进时,区间来(引)水问题不可忽视。
需要首先对来(引)水进行处理,把来水流量过程加在相应河段的入流过程中(引水视为负来水)。
对有相应来(引)水资料的河段,可以考虑将区间来水分为两部分处理,一是基础部分,将其平均分配到整个计算过程中;其余部分只分配在涨洪段,分配比例应与上游断面的入流量建立相应函数关系。
对于支流有先演后合和先合后演法,先演后合法是对演算河段干、支流分别建立马斯京根演算模型,推求出各河段洪水出流过程后,在出流断面进行线性叠加求得出流过程,适用于地形或坡度比较陡,干、支流相互影响较小的地区。
传统的先演后合法在没有各支流单独涨水的洪水资料时,采用各支流x值与干流相同且K值与河长成正比的方法。
有学者认为,先演后合法整体精度优于先合后演法,其原因主要是由于前者更充分地考虑了河道特性对洪水变化的影响。
先演后合法中分河段演算精度又优于整河段,再者分河段有预见期而整河段无预见期。