重心法选址计算题目

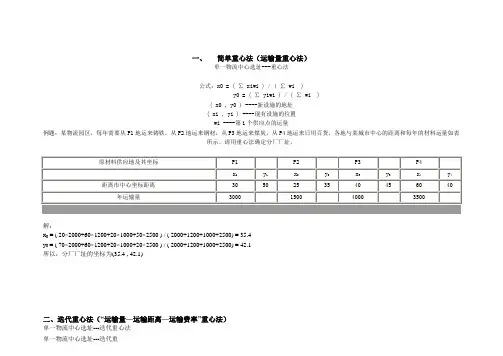
一、简单重心法（运输量重心法）单一物流中心选址---重心法公式：x0 = ( ∑ xiwi ) / ( ∑ wi)y0 = ( ∑ yiwi ) / ( ∑ wi)( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题：某物流园区，每年需要从P1地运来铸铁，从P2地运来钢材，从P3地运来煤炭，从P4地运来日用百货，各地与某城市中心的距离和每年的材料运量如表所示。

请用重心法确定分厂厂址。

解：x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以，分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法（“运输量—运输距离—运输费率”重心法）单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式：X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法：（1）令Di=1A、求出仓库的初始位置；B、将求出的仓库位置（X，Y）代入Di公式中，求出客户到仓库初始位置的距离；C、计算出仓库初始位置的总运费ΣQiRiDi；( 2 ) 迭代计算：A、将Di代入原公式，求出仓库的新位置坐标（X ，Y）；B、将求出的（X ，Y）代入Di公式中求出Di；C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代，直到求出的仓库位置和总运费越来越接近于不变，即为所得；注意：牵涉到运输费率要用重心法做；但如无费率，又要求用迭代重心法计算，则令费率为1。

配送中心选址的基本方法（一）单一配送中心的选址单一配送中心的选址方法有重心法、数值分析法等。

现以重心法为例进行计算说明。

1．重心法模型如图9-7所示，设有n 顾客，它们各自的坐标是()i i y x ,(i=1,2,3…,n)，配送中心的坐标是()00,y x ，有∑==nj jC H 1 （9-1）式中 H ---从配送中心到各顾客的总运输费用；jC -----从配送中心到各顾客的运输费用 而jC 又可以用下式来表示jj j j d w h C = （9-2）式中h: 表示从配送中心到顾客j 的运输费率 w : 表示从配送中心到零售店j 的发送量 jd ：从配送中心到顾客的运距。

jd 也可以写成如下形式()()[]212020j j j y y x x d -+-= （9-3）把（4-2）代入（4-1）中，得到jj nj j d w h H ∑==1（9-4）从式（9-3）和（9-4），可求出使H 为最小的0x 、y 。

解决这个问题的方法是运用下面的计算公式，令()0010=-=∂∂∑=j j j n j j d x x w h x H（9-5） ()0010=-=∂∂∑=j j j n j j d y y w h y H（9-6）从式（9-5）和式（9-6）中可分别求得最适合的*0x 和*0y ，即∑∑===dwh d x whx // （9-7）∑∑===dwh d y wh y 11*0// （9-8）因式（9-7）和式（9-8）右边还含有jd ，即还含有要求的未知数0x 、y ，而要从两式的右边完全消去0x 和y ，计算起来很复杂，故采用迭代法来进行计算。

2．迭代法的计算步骤（1）以所有顾客的重心坐标作为配送中心的初始地点（00x ，00y ）；（2）利用式（9-3）和（9-4），计算与（00x ，00y ）相应的总运费0H ；（3）把（00x ，00y ）分别代入式（9-3）、式（9-7）和式（9-8）中，计算配送中心的改善地点（10x ，10y ）；（4）利用式（9-3）和式（9-4），计算与（10x ，10y ）相应的总运费1H ；（5）把1H 和0H 进行比较，如果1H ＜0H ，则返回（3）的计算，再把（00x ，00y ）代入式（9-3）、式（9-7）和式（9-8）中，计算配送中心的再改善地点（20x ，20y ）。

工厂选址重心法实际案例老张打算开一家新工厂，生产那种超酷的智能小玩意儿。

这工厂选址可把老张愁坏了，不过呢，他听说了一个很厉害的方法叫重心法，就决定试试。

老张先把他的原料供应地和产品销售市场都列了出来。

比如说，他有三个主要的原料供应地，A地、B地和C地。

A地呢，是个大矿场，能提供生产小玩意儿的关键稀有金属，每个月能供应大概100吨原料；B地是个塑料大厂，提供的那种特殊塑料每个月能有80吨；C地则有一些电子元件，每个月供应量是50吨。

然后再看销售市场，有X城、Y城和Z城。

X城可是个大城市，对他的智能小玩意儿需求量特别大，每个月估计能卖掉200件；Y城稍微小一点，但也不错，每个月能消化150件；Z城是个新兴城市，每个月大概能卖100件。

老张就开始用重心法计算了。

他先在地图上把这些地方的坐标标出来，就像玩寻宝游戏找宝藏的位置一样。

他把A地的坐标设为（x1，y1），B地是（x2，y2），C地是（x3，y3），X城是（x4，y4），Y城是（x5，y5），Z城是（x6，y6）。

接着按照重心法的公式，先算原料供应的重心。

就好比是这些原料供应地在拔河，看最后这个平衡点在哪。

计算过程有点像在做一道复杂的数学题，不过老张也不害怕。

算出来原料供应的重心大概在一个叫M的地方。

然后再算销售市场的重心，这个又像是另一场拔河比赛，是各个销售市场在“拉扯”这个理想的工厂位置。

算出来销售市场的重心在N地。

但是呢，老张也不能只看这两个重心就决定工厂位置呀。

他还得考虑一些其他的因素，就像在做蛋糕的时候，除了面粉和糖，还得看看有没有鸡蛋和牛奶这些其他重要的东西。

比如说，M地虽然是原料供应的重心，但是那地方交通不太方便，运输成本还是很高；N地虽然靠近销售市场重心，但是当地的劳动力成本特别高，这可不行，老张还想多赚点钱呢。

于是老张就在M地和N地之间找了一个折中的地方，叫P地。

P地交通还不错，离高速公路和铁路都比较近，这样原料运输方便；而且当地劳动力资源丰富，工资也比较合理。

重心法选址项目分析实例答：重心法包括基于需求量的重心法和基于吨距离的重心法等两种方法。

基于需求量的重心解法：把需求量作为考察因素，它的主要步骤是首先将一个经济区域内的各需求点在坐标系中表示，并将各需求点看成一个物理系统，然后将各需求点的需求量视为物体的质量，最后通过求该物理系统的重心来确定物流中心的最佳坐落点。

基于吨距离的重心法解法：因是单一设施选址，物流中心的建设以及运营成本均可以视为固定不变的，而运输费用随距离和货运量而变化，所以可以考虑在不同地点设置的物流中心因距各用户距离变化和需求量而引起运输费用的变化，找出使运输总费用最小的点，并将其作为最佳选址点。

（4）重心法选址计算：x0 = ( 30×2200+70×1800+30×1500+60×2500 ) / ( 2200+1800+1500+2500) = 48.38 y0 = ( 80×2200+70×1800+30×1500+30×2500 ) / (2200+1800+1500+2500) = 52.75所以，分厂厂址的坐标为(48.38 , 52.75)例题二：某汽车公司，每年需要从A ，地运来橡胶，从AZ 地运来玻璃，从A ：地运来发动机，从A 、地运来零配件，各地与某城市中心的距离和每年的材料运量如表。

假设城市的中心为原点，各种材料运输费率相同，用重心法确定该公司合理位置。

解：设重心坐标为（X O ,Y O ），则根据重心法公式计算如下：0x =∑∑==4141j j jj jj j W C x W C =29001300150030002900*501300*401500*1003000*45++++++=55.4km; 0y =∑∑==4141j j jj jj j W C y W C =29001300150030002900*801300*101500*703000*60++++++=60.92km 即该公司的合理位置的坐标为（55.4 , 60.92 ）。

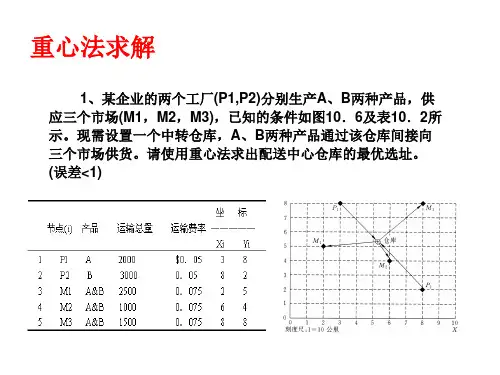
基于重心法的仓库选址方法分析摘要：在物流管理实践中，仓库选址是个很普遍的问题，如果盲目地进行仓储的选址与规划就会造成巨大的浪费。

而在解决这一问题的方法多样，有因素评分法、线性规划法和重心法。

其中，精确重心法是常用且有效的一种，通过控制总运输成本最低，从而在多个生产地和需求地区域内找到重心，设为仓库点。

但此方法并不适用于考虑实际地形、以及仓库建设成本的实际仓库选址问题，本文将对以上两种问题分析比较，并针对考虑建设成本的仓库选址问题进行实例分析。

一仓库选址问题概述在物流网络中，仓库连接着供应点和需求点，是两者之间的桥梁，在物流系统中起着重要作用。

选址在整个物流系统中占有重要的地位,是属于物流管理战略层的研究问题，仓储系统选址对企业商品流转速度和流通费用产生直接影响，并关于到企业对顾客的服务水平和服务质量。

如果不好好利用，反之盲目地进行仓储的选址与规划就会造成巨大的资源浪费，同时给企业经营带来很多不良后果。

二基于重心法原理的仓库选址问题1.重心法原理物流网络中仓库选址的实践中常用的方法是精确重心法（又称重心法）。

重心法是一种模拟方法，它将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心作为物流网点的最佳设置点，利用求物体系统重心的方法来确定物流网点的位置。

这种方法主要考虑的因素是现有设施之间的距离和要运输的货物量，将商品运输量作为影响商品运输费用的主要因素，仓库尽可能接近运量较大的网点，从而使较大的商品运量走相对较短的路程，就是求出本地区实际商品运输费用的重心所在的位置。

2.单个仓库选址理论模型重心法作为单一设施选址问题中最基本的方法之一，使用较为频繁，为了便于探讨问题,理想的重心法理论模型作出以下假设：只考虑现有设施之间的距离和要运输的货物量，1)模型常常假设需求量集中于某一点，各个需求点的位置和需求量已知而且不变，且运入和运出成本是相等的，不考虑在不满载的情况下增加的特殊运输费用；2)模型没有区分在不同地点建设仓库所需的资本成本,以及与在不同地点经营有关的其他成本的差别,而只是计算运输成本；3)模型中仓库与其他网络节点之间的路线通常是假定为直线，且运输费用只与配送中心和需求点的直线距离有关，不考虑城市交通状况；4)模型只考虑现有设施之间的距离和要运输的货物量，不考虑未来收入和成本及其他变化。

重心法重心法是将物流系统的需求点看成是分布在某一平面范围内的物体系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心将作为物流网点的最佳设置点，利用确定物体中心的方法来确定物流网点的位置。

具体过程如下。

设在某计划区域内，有N 个资源点和需求点，各点的资源量或需求量为),,2,1(n j W j =，它们各自的坐标是),,2,1)(,(n j y x j j =。

该网络用图5-2示如下：在计划区域内准备设置一个配送中心，设该配送中心的坐标是),(y x ，配送中心至资源点或需求点的运费率是jC 。

根据求平面中物体重心的方法，可以得到：⎪⎪⎩⎪⎪⎨⎧==∑∑∑∑====n j nj j j j j j n j nj j j j j j W C Y W C y W C X W C x 1111 （5-15）代入数值，实际求得),(y x 的值，即为所求得配送网点位置的坐标。

必须指出的是，通过上述方法求得的配送中心坐标还不是最优的，因为它没有考虑设置一个配送中心后现有资源点和需求点之间将不再直接联系而要通过该配送中心中转，运输距离将发生变化，从而运输成本也将变化。

所以必须将以上方法加以如下优化。

假设配送中心的地理坐标是),(00y x 。

配送中心到资源点或者需求点的发送费用为jC ，总的发送费用为D ，则有：∑==nj jC D 1（5-16）而jC 又可以用下面的式子来表示：jj j j d W r C = （5-17）式（5-17）中：j r——从配送中心到资源点或者需求点的发送费率（即单位吨公里的发送费）；jW ——资源点的供应量或者需求点的发送量；jd ——从配送中心到资源点或者需求点的直线距离。

其中，jd 也可以写成如下形式：][)(2)(2021j jj y yx x d --=- （5-18）把方程式（5-18）代入（5-17），得到：∑==nj jj j d W r D 1（5-19）从方程式（5-19）和方程式（5-16）可以求得使D 为最小的),(00y x 。

选址决策练习一、重心法1、例题某公司拟建一仓库，由2个工厂（P1、P2）向仓库供货，再由仓库供应3个分销中心（M1、M2、M3）。

各工厂、分销中心的坐标、货运量及运费率如下表所示。

请用重心法选址使运输成本最小。

解：（1）建表格求解简化计算（2）求解Xd、YdXd=3225.00/625=5.16；Yd=3237.50/625=5.182、练习1）某轻化集团公司生产多种轻化产品，其中洗衣粉、香皂两种产品主要供应五个目标市场（W1、W2、W3、W4、W5）。

各个目标市场的年销售量、运输费率及地理坐标如下表所示。

现公司欲设置一区域分销配送中心向五个市场供货，请用重心法确定该分销配送中心的位置。

解：I Xi Yi W H HW HWX HWY1 3 8 5000 0.04 200 600 48002 8 2 7000 0.04 280 2240 5603 2 5 3500 0.05 175 350 8754 8 8 3000 0.06 180 **** ****5 6 4 5500 0.05 275 1650 1100∑1110 6280 8775 得到：Xi=6280/1110=5.66 Yi=8775/1110=7.912）某物流公司拟建一配送中心负责向四个工厂进行物料供应配送，个工厂的具体位置与年物料配送量见下表，设物流公司拟建的配送中心对各工厂的单位运输成本相等。

请利用重心法确定该配送中心位置。

解：i Xi Yi w h hw Hwx Hwy1 20 70 2000 1 2000 40000 1400002 60 60 1200 1 1200 72000 720003 20 20 1000 1 1000 20000 200004 50 20 2500 1 2500 125000 50000∑6700 257000 282000 解：Xi=257000/6700=38.35Yi=282000/6700=42.09二、盈亏平衡分析法1、例题M物流重心在H市初选了3个可选地，3个选址方案作为较好方案预计发生的物流成本如下表所示，试从成本角度定量分析3个方案并确定最优方案。

《物流系统规划》——第四章：物流网络与选址作业
班级：学号：姓名：
1.盈亏点平衡法
某外资企业拟在国内新建一条生产线，确定了三个备选场址，由于各场址土地费用、建设费用、原材料成本不尽相同，从而生产成本也不相同，三个场址的生产成本已经计算如下表，试确定最佳场址。

2.重心法
某机器制造厂，每年分别从P1，P2，P3三地运钢材、铸铁、焦碳。

距离如下表所示，运输费用相同。

试用重心法确定合理位置。

并试用数值分析法对以上最佳方案进行优化。

3. 线性规划法
某企业通过两家工厂F1、F2向A、B、C、D四个售货点供货。

现欲设另一工厂，可供选择场址的地点为F3、F4，产品的生产成本与运输费用如下表，试确定最佳场址。

4.加权因素法
现设定A=4分，E=3分，I=2分，O=1分，U=0分
分级加权评分法选择场址举例
5.因次分析法
某公司拟建一爆竹加工厂，有三处待选场址A、B、C，重要经济因素成本如表所示，非经济因素主要考虑政策法规、气候因素和安全因素。

就政策而言，A地最宽松，B地次之，C地最次；就气候而言A地，B地相平，C地次之；就安全而言，C地最好，A地最差。

据专家评估，三种非经济因素比重为0.5，0.4和0.1。

要求用因次分析法确定最佳场址。

（注：主观因素比重值为0.3）。