计算题：重心法选址、因次分析法选址

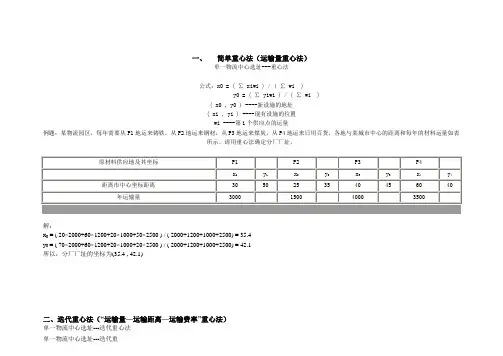
一、简单重心法（运输量重心法）单一物流中心选址---重心法公式：x0 = ( ∑ xiwi ) / ( ∑ wi)y0 = ( ∑ yiwi ) / ( ∑ wi)( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题：某物流园区，每年需要从P1地运来铸铁，从P2地运来钢材，从P3地运来煤炭，从P4地运来日用百货，各地与某城市中心的距离和每年的材料运量如表所示。

请用重心法确定分厂厂址。

解：x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以，分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法（“运输量—运输距离—运输费率”重心法）单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式：X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法：（1）令Di=1A、求出仓库的初始位置；B、将求出的仓库位置（X，Y）代入Di公式中，求出客户到仓库初始位置的距离；C、计算出仓库初始位置的总运费ΣQiRiDi；( 2 ) 迭代计算：A、将Di代入原公式，求出仓库的新位置坐标（X ，Y）；B、将求出的（X ，Y）代入Di公式中求出Di；C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代，直到求出的仓库位置和总运费越来越接近于不变，即为所得；注意：牵涉到运输费率要用重心法做；但如无费率，又要求用迭代重心法计算，则令费率为1。

配送中心选址的基本方法（一）单一配送中心的选址单一配送中心的选址方法有重心法、数值分析法等。

现以重心法为例进行计算说明。

1．重心法模型如图9-7所示，设有n顾客，它们各自的坐标是()iiyx,(i=1,2,3…,n)，配送中心的坐标是(),yx，有∑==njjCH1（9-1）式中H---从配送中心到各顾客的总运输费用；jC-----从配送中心到各顾客的运输费用而jC又可以用下式来表示jjjjdwhC=（9-2）式中h: 表示从配送中心到顾客j的运输费率w: 表示从配送中心到零售店j的发送量jd：从配送中心到顾客的运距。

jd也可以写成如下形式()()[]21220jjjyyxxd-+-=（9-3）把（4-2）代入（4-1）中，得到jj nj j d w h H ∑==1（9-4）从式（9-3）和（9-4），可求出使H 为最小的0x 、y 。

解决这个问题的方法是运用下面的计算公式，令()0010=-=∂∂∑=j j j n j j d x x w h x H（9-5） ()0010=-=∂∂∑=j j j nj j d y y w h y H（9-6）从式（9-5）和式（9-6）中可分别求得最适合的*0x 和*0y ，即∑∑===dwh d x whx // （9-7）∑∑===dwh d y wh y 11*0// （9-8）因式（9-7）和式（9-8）右边还含有jd ，即还含有要求的未知数0x 、y ，而要从两式的右边完全消去0x 和y ，计算起来很复杂，故采用迭代法来进行计算。

2．迭代法的计算步骤（1）以所有顾客的重心坐标作为配送中心的初始地点（00x ，00y ）；（2）利用式（9-3）和（9-4），计算与（00x ，00y ）相应的总运费0H ；（3）把（00x ，00y ）分别代入式（9-3）、式（9-7）和式（9-8）中，计算配送中心的改善地点（10x ，10y ）； （4）利用式（9-3）和式（9-4），计算与（10x ，10y ）相应的总运费1H ；（5）把1H 和0H 进行比较，如果1H ＜0H ，则返回（3）的计算，再把（00x ，00y ）代入式（9-3）、式（9-7）和式（9-8）中，计算配送中心的再改善地点（20x ，20y ）。

《物流系统规划》——第四章：物流网络与选址作业
班级：学号：姓名：
1.盈亏点平衡法
某外资企业拟在国内新建一条生产线，确定了三个备选场址，由于各场址土地费用、建设费用、原材料成本不尽相同，从而生产成本也不相同，三个场址的生产成本已经计算如下表，试确定最佳场址。

2.重心法
某机器制造厂，每年分别从P1，P2，P3三地运钢材、铸铁、焦碳。

距离如下表所示，运输费用相同。

试用重心法确定合理位置。

并试用数值分析法对以上最佳方案进行优化。

3. 线性规划法
某企业通过两家工厂F1、F2向A、B、C、D四个售货点供货。

现欲设另一工厂，可供选择场址的地点为F3、F4，产品的生产成本与运输费用如下表，试确定最佳场址。

4.加权因素法
现设定A=4分，E=3分，I=2分，O=1分，U=0分
分级加权评分法选择场址举例
5.因次分析法
某公司拟建一爆竹加工厂，有三处待选场址A、B、C，重要经济因素成本如表所示，非经济因素主要考虑政策法规、气候因素和安全因素。

就政策而言，A地最宽松，B地次之，C地最次；就气候而言A地，B地相平，C地次之；就安全而言，C地最好，A地最差。

据专家评估，三种非经济因素比重为0.5，0.4和0.1。

要求用因次分析法确定最佳场址。

（注：主观因素比重值为0.3）。

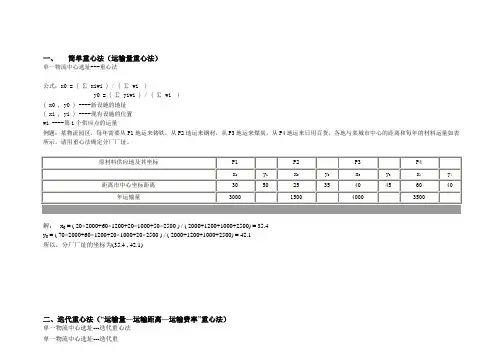
一、简单重心法（运输量重心法）单一物流中心选址---重心法公式：x0 = ( ∑ xiwi ) / ( ∑ wi )y0 = ( ∑ yiwi ) / ( ∑ wi )( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题：某物流园区，每年需要从P1地运来铸铁，从P2地运来钢材，从P3地运来煤炭，从P4地运来日用百货，各地与某城市中心的距离和每年的材料运量如表所示。

请用重心法确定分厂厂址。

解：x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以，分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法（“运输量—运输距离—运输费率”重心法）单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式：X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法：（1）令Di=1A、求出仓库的初始位置；B、将求出的仓库位置（X，Y）代入Di公式中，求出客户到仓库初始位置的距离；C、计算出仓库初始位置的总运费ΣQiRiDi；( 2 ) 迭代计算：A、将Di代入原公式，求出仓库的新位置坐标（X ，Y）；B、将求出的（X ，Y）代入Di公式中求出Di；C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代，直到求出的仓库位置和总运费越来越接近于不变，即为所得；注意：牵涉到运输费率要用重心法做；但如无费率，又要求用迭代重心法计算，则令费率为1。

一、简单重心法（运输量重心法）单一物流中心选址---重心法公式：x0 = ( ∑ xiwi ) / ( ∑ wi )y0 = ( ∑ yiwi ) / ( ∑ wi )( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题：某物流园区，每年需要从P1地运来铸铁，从P2地运来钢材，从P3地运来煤炭，从P4地运来日用百货，各地与某城市中心的距离和每年的材料运量如表所示。

请用重心法确定分厂厂址。

解：x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以，分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法（“运输量—运输距离—运输费率”重心法）单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式：X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法：（1）令Di=1A、求出仓库的初始位置；B、将求出的仓库位置（X，Y）代入Di公式中，求出客户到仓库初始位置的距离；C、计算出仓库初始位置的总运费ΣQiRiDi；( 2 ) 迭代计算：A、将Di代入原公式，求出仓库的新位置坐标（X ，Y）；B、将求出的（X ，Y）代入Di公式中求出Di；C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代，直到求出的仓库位置和总运费越来越接近于不变，即为所得；注意：牵涉到运输费率要用重心法做；但如无费率，又要求用迭代重心法计算，则令费率为1。

重心法在油库选址问题中的应用文章标题：重心法在油库选址问题中的应用一、引言在油库选址问题中，重心法是一种常用的方法，它能够帮助我们寻找最佳的位置来建设油库。

在本文中，我将从简单到复杂，由浅入深地探讨重心法在油库选址中的应用。

我将首先介绍重心法的基本原理和计算方法，然后详细分析它在油库选址中的具体应用，最后总结和回顾本文内容，共享个人观点和理解。

二、重心法的基本原理和计算方法重心法是一种通过计算各个要素的重心位置来确定最佳位置的方法。

在油库选址中，我们需要考虑诸多因素，比如土地的稳定性、交通便利程度、环境保护等等。

通过重心法，我们可以将这些因素量化，然后计算它们的重心位置，从而找到最佳的建设位置。

重心的计算方法一般有几种，比如代数法、几何法和矢量法。

在油库选址中，我们可以根据具体情况选择合适的计算方法，并结合地理信息系统（GIS）等技术，来精确计算各项因素的重心位置，从而得到最佳的建设位置。

三、重心法在油库选址中的应用1. 土地的稳定性在选择油库的位置时，土地的稳定性是一个非常重要的因素。

通过重心法，我们可以将土地的稳定性量化，并计算出它的重心位置。

通过比较不同地点的稳定性重心位置，可以找到最佳的建设位置，从而确保油库的安全。

2. 交通便利程度油库的选址还需要考虑交通便利程度。

通过重心法，我们可以计算各个交通节点的位置重心，从而找到最佳的建设位置。

这可以确保油库的运输效率和便利程度，节省运输成本。

3. 环境保护在油库选址中，环境保护也是一个必须考虑的因素。

通过重心法，我们可以计算各个环境指标的重心位置，从而找到最佳的建设位置。

这可以最大程度地减少对环境的影响，保护生态环境。

四、总结和回顾通过本文的讨论，我们可以看到重心法在油库选址中的重要性和应用。

通过重心法，我们可以将各个因素量化，精确计算它们的重心位置，从而找到最佳的建设位置。

重心法不仅可以帮助我们解决油库选址问题，也可以在其他领域得到应用。

个人观点和理解从我个人的角度来看，重心法是一种非常实用的方法，在油库选址中有着广泛的应用价值。

层次分析法及中心选址问题汉派服装配送及仓储中心选址材料案例背景汉派服装曾是武汉的一块招牌，上世纪90年代初期，凭借起步较早的产业结构和九省通衢的地理环境优势，汉派服装以大众化、平民化的风格逐步名扬海内外。

然而，从90年代末期，汉派服饰逐渐开始走下坡路。

2014年3 月北京举行亚洲最大规模的服饰博览会，8家武汉服装企业组团上演惊艳“汉秀”。

经历十年阵痛蛰伏期后，武汉服装开始擦亮“新汉派”招牌。

武汉市3年将投入6000万元专项资金，支持在汉服装企业发展，以期在2019年，实现全市纺织服装产业产值突破1000亿元。

昨日，武汉市政府常务会通过《武汉市振兴汉派服装产业转型规划(2014-2019)»，计划将“汉派服装”打造成新千亿产业。

为了汉派服装的正兴，相关企业拟投资建设专用的集流通、加工、包装为一体的集合式配送中心，此次汉派服装重点针对的市场细分人群为大学生，这一部分人消费观点前卫，可以接受电子商务模式且聚集地相对集中在武昌区。

汉派服饰生产基地位于硚口区的古田地段毗邻汉正街但是相对地价来说较高，但是有完善的物流配套设施和全国闻名的知晓度，不需要太多的宣传费用就家喻户晓；黄陂区相对中心城区地价相对便宜，但是周边配套设施又不健全，人流量规模相对较少，但是周边空地多，方便扩建；光谷周边的高新科技区属于国家示范创业园，有相对的政策扶持如减免企业所得税等，但是光谷周边近5年都要修建地铁、地下商城、火车站等大型项目，交通相对5年来说又不便利。

以下有3处待选之地供企业选择，请结合层次分析法和专家打分法，做出最优判断，并说明理由。

A地：东湖新技术开发区位于武汉市东南部洪山区，江夏区境内。

下辖8个街道。

在东湖、南湖和汤逊湖之间，东起武汉外环线，西至卓刀泉路，北接东湖，南临汤逊湖，面积518.06平方公里，常住人口190.6万。

由关东光电子产业园、关南生物医药产业园、汤逊湖大学科技园、光谷软件园、佛祖岭产业园、机电产业园等园区组成。

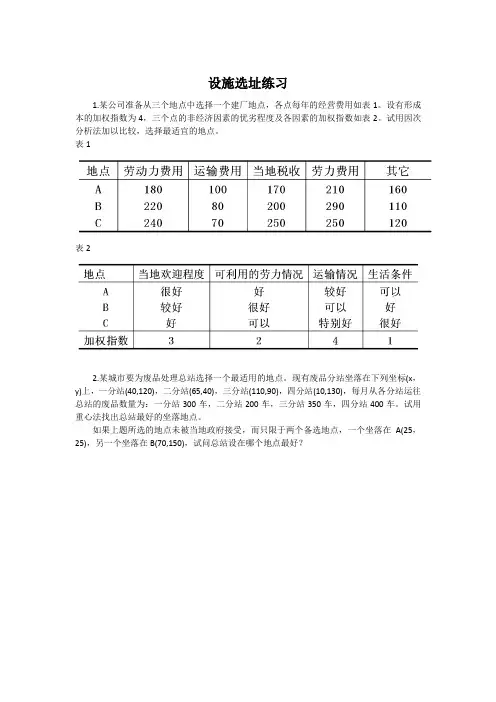
设施选址练习
1.某公司准备从三个地点中选择一个建厂地点，各点每年的经营费用如表1。

设有形成本的加权指数为4，三个点的非经济因素的优劣程度及各因素的加权指数如表2。

试用因次分析法加以比较，选择最适宜的地点。

表1
表2
2.某城市要为废品处理总站选择一个最适用的地点。

现有废品分站坐落在下列坐标(x，y)上，一分站(40,120)，二分站(65,40)，三分站(110,90)，四分站(10,130)，每月从各分站运往总站的废品数量为：一分站300车，二分站200车，三分站350车，四分站400车。

试用重心法找出总站最好的坐落地点。

如果上题所选的地点未被当地政府接受，而只限于两个备选地点，一个坐落在A(25，25)，另一个坐落在B(70,150)，试问总站设在哪个地点最好？。

2021年11月高级物流师考试计算题应试解析（10）已知ABC公司与库存的有关信息如下：(1)年需求数量为30000单位(假设每年360天);(2)购买价格每单位100元;(3)仓库储存成本是商品买价的30%;(4)订货成本每次60元;(5)公司希望的安全储备量为750单位;(6)订货的数量只能按100的倍数(四舍五入)确定;(7)订货至到货的时间为15天。

要求：(1) 经济订货量为多少?(2) 存货水平为多少时应补充订货?(3) 存货平均占用多少资金?解：(1)(2)再订货点=平均日需求x订货天数+安全储备量=30000/360x15+750=1250+750=2000(单位)(3)占用资金=(采购批量/2)x单价+安全储备量x单价=(300/2)x100+750x100=90000(元)2021年11月高级物流师考试计算题应试解析（9）某仓储企业投资项目有三个可行方案，建设周期分别为2年、3年和4年，其投资均为银行贷款，利率为15%。

这三个方案各年的投资额度(年初投入)以及建成后各年的盈利情况如下表。

(已知：(P/F,15%，1)=0.870; (P/F,15%，2)=0.757; ( P/F,15%，3)=0.658;(P/F,15%，4)=0.572;(P/F,15%,5) =0.497;(P/F,15%,6) = 0.432; (P/F,15%,7) =0.376;(P/F,15%,8)=0.327;(P/F,15%,9) =0.284;方案一方案二方案三年度投资利润年度投资利润年度投资利润1 80 1 60 1 402 90 2 70 2 503 3 3 504 40 4 30 45 50 5 40 5 506 60 6 50 6 657 60 7 60 7 608 70 8 50 8 70问题：1、长期投资决策有哪几种计算方法?2、长期投资时为什么要进行现值计算?3、运用现值指数法进行项目决策，并按不折现的情况计算各方案的投资利润率。

2单设施重心法选址2. 1实验目掌握单设施重心法选址原理，能够计算简单选址题目中待选设施位置; 掌握单设施重心选址算法流程，能够设计类似题目算法流程，并编写程序。

2. 2实验过程(1)单设施重心法选址原理重心法选址模型示意图如图2-1所示。

图2-1单设施重心法选址选址示意图求解目标：C-总成本最低MinC^fy i d li=\其中：f厂序号为i点运输费率；V厂序号为i点产量或者销量；d厂序号为i点到待选设施点相对距离。

待选设施位置计算公式：（丈- 7=1（土少//）(工邪/〃「)/=!其中：Xc-重心X坐标;Yc-重心Y坐标；X厂第i个地点X坐标；Y厂第i个地点Y坐标；4 7以厂£$ +(Z•-〃iyX(2)算法流程图，如图2-2所示。

图2-2算法流程图2. 3实验结果(1)单设施重心法选址程序参数设定及其求解界面如图2-3所示。

图2-3单设施重心法选址程序参数设定及其求解界面(2)参数设定及其求解界面变量声明部分(代码)Private Sub Commandl_Click()If Textl. Text 二"” ThenMsgBox 〃X-横坐标不允许为空〃Textl・ SetFocusExit SubElself IsNumeric(Textl・Text)二False ThenMsgBox 〃X-横坐标必须为数值型数据！〃Textl. Text 二"”Textl・ SetFocusExit SubEnd IfIf Text2・Text 二"” ThenMsgBox 〃Y-纵坐标不允许为空〃Text2・ SetFocusExit SubElself IsNumeric(Text2・Text)二False Then MsgBox 〃Y-纵坐标必须为数值型数据！〃Text2.Text ="”Text2・ SetFocusExit SubEnd IfIf Text3. Text 二ThenMsgBox 〃产量或销量不允许为空〃Text3・ SetFocusExit SubElself IsNumeric(Text3.Text)二False Then MsgBox 〃产量或销量应为数值型数据！〃Text3. Text ="”Exit SubMsgBox "产量或销量应为正数，否则无实际意义!Text3. Text 二Text3・ SetFocusExit SubEnd IfIf Text4.Text 二ThenMsgBox 〃运输费率不允许为空〃Text4. SetFocusExit SubElself IsNumeric(Text4・Text)二False Then MsgBox 〃运输费率应为数值型数据！”Text4. Text =Text4. SetFocusExit SubElself Vai(Text4. Text) < 0 ThenMsgBox 〃运输费率应为正数，否则无实际意义！”Text4. Text =Exit Sub End IfMsgBox 〃X0-横坐标不允许为空〃Text5・ SetFocusExit SubElself IsNumeric(Text5.Text)二False Then MsgBox 〃X0-横坐标必须为数值型数据！〃Text5. Text ="”Text5・ SetFocusExit SubEnd IfIf Text6. Text = "” ThenMsgBox 〃丫0-纵坐标不允许为空〃Text6・ SetFocusExit SubElself IsNumeric(Text6・Text)二False Then MsgBox 〃Y0-纵坐标必须为数值型数据！〃Text6. Text =Text6・ SetFocusExit SubEnd IfMsgBox 〃精度不允许为空〃Text7. SetFocusExit SubElself IsNumeric(Text7. Text) = False ThenMsgBox 〃精度应为数值型数据！〃Text7. Text ="”Text7. SetFocusExit SubElself Vai (Text7. Text) < 0 ThenMsgBox 〃精度应为正数，否则无实际意义！〃Text7. Text ="”Text7. SetFocusExit SubEnd IfFor i = 1 To Listl. ListCountIf Tex tl .Text = Vai (Listl. Lis t(i - 1)) And Tex t2. Text = Vai (List2. List(i - 1)) ThenMsgBox 〃及第〃 & i & 〃输入坐标值相同，请重新输入〃Textl.Text 二"”Text2.Text ="”Text3. Text ="”Text4. Text =""Textl. SetFocusExit SubEnd IfNext iList 1・Additem Textl.TextList2.AddItem Text2・TextList3・Addltem Text3.TextList4. Addltem Text4・TextTextl. Text 二"”Text2. Text ="”Text3.Text ="”Text4. Text =Textl・ SetFocusIf Listl・ ListCount ＞二 2 Then Command2・ Enabled 二True End IfEnd SubPrivate Sub Command2_Click()Xc = Vai(Text5. Text)Yc = Vai(Text6. Text)JD = Vai(Text7. Text)Dim SumCO As DoubleDim SumCN As DoubleDim Sumi As DoubleDim Sum2 As DoubleDim Sum3 As DoubleFor j = 1 To 10000SumCO 二0SumCN 二0Sumi 二0Sum2 二0Sum3 二0For i 二 1 To Listl・ListCountdi = Sqr ((Xc - Vai (Listl. List (i - 1))) " 2 + (Yc - Vai (List2. List (i - 1))) " 2)'距离公式SumCO 二SumCO + Val (List3・ List(i - D)* Val(List4. List(i - 1)) * diSumi 二Sumi + (Val (Listl.List(i - D)*Val (List3. List(i - 1)) * Val(List4.List(i - 1))) / diSum2 二Sum2 + (Val (List2. List(i - D)* Val (List3. List(i - 1)) * Val (List4. List(i - 1))) / diSum3 二Sum3 + (Val (List3・ List(i 一D)* Vai (List4. List(i - 1))) / diNext iXc = Sumi / Sum3Yc = Sum2 / Sum3For i 二 1 To Listl・ ListCountdi = Sqr ((Xc - Vai (Listl. List (i - 1))) 2 + (Yc - Vai (List2. List(i - 1)))八2)SumCN = SumCN + Vai (List3. List (i - 1)) * Vai (List4. List(i - 1)) * diNext iIf (SumCO - SumCN) <= JD ThenTextS・ Text 二XcText9. Text 二YcTextlO. Text 二SumCNTextl1. Text 二jExit ForEnd IfNext jEnd SubPrivate Sub Listl_Click()For i 二 1 To Listl・ListCountIf Listl・Selected(i - 1)二True Thenh = InputBoxC请输入要改参数参数修正〃)If h <> And IsNumeric (h)二True ThenListl. List (i - 1) = hElse: MsgBox 〃输入数据必须为数值型数据〃End IfEnd IfNext iEnd SubPrivate Sub List2_Click()For i = 1 To List2. ListCountIf List2.Selected(i - 1) = True Thenh = InputBoxC"请输入要改参数：“，〃参数修正〃)If h <> "” And IsNumeric(h) = True ThenList2. List (i - 1) = hElse： MsgBox 〃输入数据必须为数值型数据〃End IfEnd IfNext iEnd SubPrivate Sub List3_Click()For i = 1 To List3. ListCountIf List3.Selected(i - 1) = True Thenh = InputBoxC请输入要改参数:;'参数修正〃）If h <> "” And IsNumeric (h) = True And Vai (h) > 0 Then List3. List (i - 1) = hElse： MsgBox 〃输入数据必须为数值型数据〃End IfEnd IfNext iEnd SubPrivate Sub List4_Click()For i = 1 To List4. ListCountIf List4.Selected(i - 1) = True Thenh = InputBoxC"请输入要改参数：〃，〃参数修正〃)If h <> And IsNumeric (h) = True And Vai (h) > 0 Then List4. List (i - 1)二hElse: MsgBox 〃输入数据必须为数值型数据〃End IfEnd IfNext iEnd Sub (3)单设施重心法选址程序求解结果如图2-4所示。