时域数学模型
- 格式:pdf
- 大小:912.07 KB
- 文档页数:31

二阶系统的时域分析二阶系统的数学模型二阶系统指的是系统的动态特性可以由一个二阶微分方程描述的系统。
在控制工程中,二阶系统的时域分析主要包括对系统阶跃响应、脉冲响应、频率响应等进行分析。
下面将详细介绍二阶系统的数学模型以及各种时域分析方法。
二阶系统可以由一个二阶微分方程进行描述。
一般而言,二阶系统的数学模型可以写成如下形式:\[a_2\frac{{d^2y(t)}}{{dt^2}} + a_1\frac{{dy(t)}}{{dt}} +a_0y(t) = b_2\frac{{d^2u(t)}}{{dt^2}} + b_1\frac{{du(t)}}{{dt}}+ b_0u(t)\]其中,y(t)为系统的输出,u(t)为系统的输入,a_0、a_1、a_2以及b_0、b_1、b_2分别为系统的系数。
这个方程也可以写成常用的形式:\[\frac{{d^2y(t)}}{{dt^2}} + 2ζω_n\frac{{dy(t)}}{{dt}} +ω_n^2y(t) = K_p\frac{{d^2u(t)}}{{dt^2}} +T_i\frac{{du(t)}}{{dt}} + K_cu(t)\]其中,ζ为阻尼比,ω_n为自然频率,K_p为比例增益,T_i为积分时间常数,K_c为控制器增益。
2.二阶系统的阶跃响应阶跃响应是指系统在接受一个单位阶跃信号作为输入时的响应。
通过对二阶系统的数学模型应用拉普拉斯变换,可以得到系统的传递函数。
对于一个传递函数为G(s)的系统,其阶跃响应可以通过下面的公式得到:\[y(t) = A(1 - e^{-ζω_nt}\cos(ω_d t + ϕ))\]其中,A为阶跃响应的幅度,ω_d为阻尼振荡角频率,ϕ为相位角。
3.二阶系统的脉冲响应脉冲响应是指系统在接受一个单位脉冲信号作为输入时的响应。
与阶跃响应类似,通过对二阶系统的数学模型进行拉普拉斯变换,可以得到系统的传递函数。
对于一个传递函数为G(s)的系统,其脉冲响应可以通过下面的公式得到:\[y(t) = \frac{{A(1 - e^{-ζω_nt}\cos(ω_d t + ϕ))}}{{\sqrt{1-ζ^2}}}\]其中,A为单位脉冲信号的幅度。



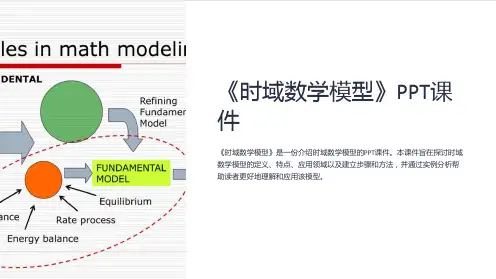


二阶系统的时域分析二阶系统的数学模型二阶系统是指由两个一阶系统级联或并联组成的动态系统。
它的数学模型可以表示为如下形式:$$s^2Y(s) + 2ξω_nsY(s) + ω_n^2Y(s) = X(s)$$其中,$s$是复频域变量,$Y(s)$和$X(s)$分别是系统的输出和输入拉普拉斯变换形式;$ξ$是阻尼比,$ω_n$是自然频率。
为了进行时域分析,我们需要将模型转换为时域表示。
我们可以通过拉普拉斯逆变换对模型进行求解。
首先,我们可以将拉普拉斯变换模型转换为分母为二次方程的形式:$$s^2 + 2ξω_ns + ω_n^2 = 0$$这是一个特征方程,也称为二阶系统的特征方程。
根据特征方程的解,我们可以获得系统的阻尼比和自然频率。
特别地,当阻尼比$ξ$小于1时,系统被称为欠阻尼;当阻尼比$ξ$等于1时,系统被称为临界阻尼;当阻尼比$ξ$大于1时,系统被称为过阻尼。
根据不同的阻尼比,我们可以对系统的时域响应进行分类:1.欠阻尼情况下,系统的时域响应会产生振荡。
振荡的频率为阻尼比与自然频率的乘积。
2.临界阻尼情况下,系统的时域响应会趋于稳定,但不会产生振荡。
3.过阻尼情况下,系统的时域响应会趋于稳定,没有振荡,并且速度较快。
在实际应用中,我们经常需要对二阶系统的时域响应进行分析和设计。
常见的时域响应指标包括步响应、阶跃响应和频率响应。
这些响应可以通过对特征方程进行求解来获得。
对于步响应,我们可以通过求解特征方程的根来获得系统的过渡时间、最大超调量和静态误差等信息。
通过调整控制器和系统参数,我们可以改变这些指标,以满足系统设计的要求。
对于阶跃响应,我们可以通过求解特征方程的根来获得系统的上升时间、峰值时间和调节时间等信息。
同样,通过调整控制器和系统参数,我们可以改变这些指标,以满足系统设计的要求。
对于频率响应,我们可以通过将特征方程转换为复频域变量来获得系统的频率响应函数。
频率响应函数可以帮助我们分析系统在不同频率下的增益和相位变化。


时域中常用的数学模型1.引言1.1 概述概述部分的内容可以按照以下方式编写:概述一节将介绍时域中常用的数学模型。
时域是指针对信号的时序特性进行建模和分析的领域,它关注信号随时间的变化过程。
在许多实际问题中,我们需要利用数学模型来描述和分析信号在时域上的行为。
通过建立适当的数学模型,我们可以深入理解信号的特点和规律,为问题的解决提供依据。
本文将主要介绍两种常用的时域数学模型。
第一种模型是XXX模型,它在解决问题时广泛应用于XXX领域。
XXX模型基于XXX原理,通过XXX方式来描述信号在时域上的变化。
该模型具有XXX的特点,可以有效地描述XXX的过程和行为。
第二种模型是XXX模型,它是XXX领域的一种主要数学工具。
XXX模型通过XXX方法来描述信号在时域上的演化过程,具有XXX的特点和优势。
本文的主要目的是介绍这两种常用的数学模型,深入探讨它们的原理和应用。
通过对这些模型的学习和理解,我们可以更好地应用它们解决实际问题。
此外,本文还将对这两种模型进行比较和分析,探讨它们的优劣和适用范围。
最后,本文将给出一些结论和展望,以期对读者更好地理解和应用时域中常用的数学模型提供帮助。
在下一节中,我们将重点介绍数学模型1。
通过对数学模型1的详细分析,我们将深入了解它的原理、特点和应用。
请继续阅读下一节,以获取更多有关数学模型1的内容。
以上便是概述部分的内容。
这部分主要对整篇文章进行开场引言,介绍文章将要讨论的内容和目的,为读者打下阅读的基础。
1.2文章结构文章结构部分的内容可以按照以下方式编写:1.2 文章结构本文将按照以下结构来介绍时域中常用的数学模型。
2. 正文2.1 数学模型12.2 数学模型2在正文部分,我们将详细介绍两个时域中常用的数学模型。
通过对每个数学模型的原理、应用场景以及解决问题的方法进行分析和说明,读者将能够深入了解数学模型在时域中的作用和应用。
3. 结论3.1 总结3.2 展望结论部分将对本文的主要内容进行总结,并展望未来时域中数学模型的发展趋势和研究方向。

电容的时域表达式
纯电阻电路
只有含有电阻(纯电阻负载)的交流电路成为纯电阻电路。
例:白炽灯、电阻炉、电烙铁等。
时域数学模型: u(t)=R i(t)
电容电路
如果把电接到交流电源上,由于交变电压时刻在变化,电极板上的电荷也就时刻在交替发生充放电,使电路中有电流流通,即呈通路状态。
电容量不同,电流也不相同。
时域数学模型: q(t)=Cu(t)
u(t)=\frac{1}{C} \int_{0}^{t}i(t) dt
电感电路
电感线圈是电工电子技术中最常用的元件之一,象电动机、变压器、交流接触器、断路器、继电器等等电气设备。
如果线圈中通过电流,电流会产生磁场,就会有磁通穿过线圈,当电流发生变化时,穿过线圈的磁通也随着发生变化,
从而在线圈的自身引起感应电动势——自感电动势。
自感电动势具有对抗电流变化的性质。
时域数学模型: \phi(t)=Li(t)
u(t)=L\frac{di(t)}{dt}
请看。
时域的实验建模方法系统辨识方法最常用的是最小二乘法,还介绍了渐消记忆辨识算法。
沃尔什变换方法优势:通过沃尔什变换可将一组沃尔什函数的积分运算用乘积运算代替。
这正是沃尔什函数能够用作动态建模的关键所在。
响应时间归一化:因为沃尔什函数被定义在[0,1)区间内,所以,传感器响应过程的时间也要单位化.与系统辨识建模法相比,沃尔什变换法所用数据少,所建模型的阶数的,直接得出微分方程的系数,减少转接误差。
但它不是的推算法,并对数据个数有严格要求。
最大嫡谱法AR模型和多维AR模型的优缺点适用场合。
自适应方法自适应模型在一定程度上能实时地处理测量数据和估计结果,自行调整模型参数。
井随着数据的不断采入,通过递推算法,自动地对模型参数加以修正,使其接近最佳值。
即值在尚不完全掌握数据序列特性的情况下也能得到满意的模型。
自适应模型的参数是由一组观察数据的线性组合进行自适应计算得到的。
本节分别采用最小均方差(LMS)递推算法和递推最小二乘(RLS)算法,建立六维力传感器和压力传感器自适应AR模型。
神经元网络方法人工神经元网络是一个大规模的非线性动力学系统,利用它可以对复杂的系统进行描述。
BP算法BP算法(反向传播算法)是一种建立在梯度下降法基础上的有导师的学习算法r5应用较多、较为成熟的算法之一。
网络结构为:一个输人层、一个输出层和若干个隐含层。
(1)对于确定性信号嚏棋,通过学习,可确定权重,建摄的误差小于2%,不存在时序方法随时间增长而不断变大的累积误差。
对于随机性较大的信号嚏棋,通过改变权重,能够跟踪信号的随机变化,具有较强的适应性。
(2)将神经元网络应用于动态嚏棋还有许多工作可做:如,提高运算速度;根据动态标定的输入、输出数据嚏棋;多输入、多输出系统建摸等。
FLANN方法本节将函数连接型神经网络(FLANN)引入传感器的动态建模。
FLANN在其输入端使用线性无关的增强权式表达,使用单层网络就可以形成各种超平面函数,而且不需要广义的6规则训练网络点用简单的6规则或一般的递推方法就可以很快收敛。