疲劳裂纹扩展.
- 格式:doc
- 大小:492.00 KB
- 文档页数:14



材料力学之材料疲劳分析算法:断裂力学模型:实验方法与材料疲劳性能测试1 材料疲劳分析基础1.1 疲劳分析的基本概念疲劳分析是材料力学的一个重要分支,主要研究材料在循环载荷作用下逐渐产生损伤并最终导致断裂的过程。
材料在承受重复或周期性的应力时,即使应力远低于材料的静态强度极限,也可能发生疲劳破坏。
这一现象在工程设计中极为关键,因为许多结构件如桥梁、飞机部件、机械零件等,都可能在使用过程中遭受循环载荷。
1.1.1 原理与内容疲劳分析的基本概念包括:-应力幅:循环应力中最大应力与最小应力之差的一半。
-平均应力:循环应力中最大应力与最小应力的平均值。
-应力比:最小应力与最大应力的比值。
-循环次数:材料承受循环载荷的次数,直到发生疲劳破坏。
-疲劳强度:材料在特定循环次数下不发生疲劳破坏的最大应力。
1.2 疲劳损伤累积理论疲劳损伤累积理论是评估材料在不同载荷循环下累积损伤程度的理论。
其中,最著名的理论是Miner线性损伤累积理论,该理论认为材料的疲劳损伤是线性累积的,即每一次载荷循环对材料的总损伤贡献是相同的。
1.2.1 原理与内容Miner线性损伤累积理论的公式为:D=∑N i N fni=1其中:-D是总损伤度。
-N i是在应力水平i下的循环次数。
-N f是在应力水平i下材料的疲劳寿命。
1.2.2 示例代码假设我们有以下数据:-材料在应力水平100MPa下的疲劳寿命为10000次。
-材料在应力水平200MPa下的疲劳寿命为5000次。
-材料在应力水平300MPa下的疲劳寿命为2000次。
在实际应用中,材料可能在这些应力水平下分别承受了5000次、2000次和1000次循环。
1.3 S-N曲线与疲劳极限S-N曲线是描述材料疲劳性能的重要工具,它表示材料的应力水平与所能承受的循环次数之间的关系。
疲劳极限是指在无限次循环下材料能够承受而不发生疲劳破坏的最大应力。
1.3.1 原理与内容S-N曲线通常通过实验数据绘制,实验中材料样品在不同应力水平下进行循环加载,直到发生疲劳破坏,记录下每个应力水平下的循环次数。



abaqus疲劳裂纹扩展材料常数
在ABAQUS中,疲劳裂纹扩展可以使用Paris定律来描述,该定律表示裂纹扩展速率与应力强度因子之间的关系。
Paris定律的一般形式如下:
da/dN = C*(ΔK)^m
其中,da/dN表示单位循环裂纹扩展量,C和m是材料常数,ΔK 表示应力强度因子范围。
在ABAQUS中,可以通过定义材料的疲劳参数来设置材料常数C和m。
具体步骤如下:
1. 创建材料:在ABAQUS/CAE界面中,选择“材料”模块,创建材料。
2. 定义疲劳参数:在材料属性对话框中,选择“机械”选项卡,在“疲劳”部分定义疲劳参数。
常见的疲劳参数包括裂纹扩展速率曲线、C 值和m值。
3. 设置疲劳分析:在ABAQUS/CAE界面中,选择“分析”模块,创建疲劳分析步。
4. 定义载荷:在疲劳分析步对话框中,设置加载条件,包括载荷大小、加载方式和加载方向。
5. 定义边界条件:在疲劳分析步对话框中,设置边界条件,包括固
定边界条件和约束条件。
6. 运行分析:保存模型并运行分析。
通过以上步骤,可以在ABAQUS中设置材料常数C和m,并进行疲劳裂纹扩展分析。
需要注意的是,具体的材料常数需要根据材料的实际疲劳性能进行确定。

疲劳裂纹扩展门槛值一、疲劳裂纹扩展的概念和原因疲劳裂纹扩展是指材料在受到周期性载荷作用下,裂纹逐渐扩展并最终导致材料失效的过程。
其原因主要是由于材料在受到外界载荷作用下,内部微观结构发生变化,从而导致裂纹的形成和扩展。
二、疲劳裂纹扩展门槛值的定义和意义疲劳裂纹扩展门槛值是指材料在一定条件下,能够抵抗疲劳载荷作用并保持稳定状态的极限载荷值。
它是评估材料抗疲劳性能的重要指标之一。
三、影响疲劳裂纹扩展门槛值的因素1. 材料本身性质:包括强度、韧性、硬度等。
2. 处理工艺:如表面处理、加工方式等。
3. 环境因素:如温度、湿度等。
4. 载荷条件:包括载荷大小、频率等。
四、测量疲劳裂纹扩展门槛值的方法1. 交变载荷法:通过不断增加载荷幅值,观察裂纹扩展情况,确定门槛值。
2. 段落法:将试样分成若干段,在每段施加不同的载荷幅值,观察裂纹扩展情况,确定门槛值。
3. 柔性几何法:通过对试样进行特定的几何形状设计,在不同载荷下观察裂纹扩展情况,确定门槛值。
五、提高疲劳裂纹扩展门槛值的方法1. 选择合适的材料:选择具有较高强度和韧性的材料可以提高门槛值。
2. 改善处理工艺:采用表面处理等工艺可以提高门槛值。
3. 控制环境因素:控制温度、湿度等环境因素可以提高门槛值。
4. 控制载荷条件:降低载荷频率、控制载荷大小等可以提高门槛值。
5. 加强试验管理:严格控制试验过程中的误差和偏差,保证测试结果的精确性。
六、结论疲劳裂纹扩展门槛值是评估材料抗疲劳性能的重要指标,影响因素较多,测量方法也较为复杂。
提高门槛值的方法有多种,需要根据具体情况进行选择和实施。

疲劳裂纹的亚临界扩展1疲劳裂纹的亚临界扩展弹簧的断裂都是有裂纹引起的,然而裂纹尖端附近的应力场对裂纹的静止、平衡和发展都有直接的影响。
当弹簧在承受静载荷的情况下,只要其工作应力小于其临界应力,弹簧在静应力水平下工作就是安全而且可靠的,除非在工作应力2临界应力情况下,弹簧才会发生脆性破坏。
但是弹簧在承受交变应力的情况下,有时即使是在很低的应力状况下进行工作,都会出现弹簧疲劳断裂的情况。
这是因为当弹簧中有初始裂纹时,它就会在交变应力的作用下发生缓慢的扩展,当其扩展到一定状态时,弹簧就会发生断裂。
裂纹从其初始值扩展到临界值的过程,称为疲劳裂纹的亚临界扩展,也就是宏观裂纹的剩余寿命阶段。
2.弹簧脆性断裂是什么弹簧在工作时所承受的应力大致有两种情况:静应力和变应力。
这两种不同的应力作用在弹簧上时,它们会产生两种完全不同的力学性能。
弹簧受静应力所产生的破坏叫做塑性变形或者是叫做脆性断裂。
然而零件或材料受变应力的破坏则叫做疲劳断裂。
3.弹簧疲劳断裂是什么弹簧在工作时所承受的应力大致有两种情况:静应力和变应力。
这两种不同的应力作用在弹簧上时,它们会产生两种完全不同的力学性能。
弹簧受静应力所产生的破坏叫做塑性变形或者是叫做脆性断裂。
然而零件或材料受变应力的破坏则叫做疲劳断裂。
4.弹簧变应力的类型弹簧变应力的类型分为稳定性循环变应力、不稳定循环变应力、随机变应力。
稳定性循环变应力:弹簧每次循环中,最大幅值和最小幅值都不随时间变化的变应力。
不稳定循环变应力:弹簧每次循环中,最大幅值和最小幅值都随时间变化的变应力。
随机变应力:不呈现出周期性变化,而且带有偶然性的变应力。
5.弹簧材料的疲劳极限一般情况下,材料疲劳性能试验所用的小尺寸光滑圆柱试件是标准试件。
通过材料的基本S-N曲线,我们可以看到它所展示的是在恒幅对称循环应力的作用下光滑材料的裂纹萌生寿命。
在应力比一定的情况下,对一组标准试件施加不同应力幅进行试验,记录其相应疲劳寿命,就可以得到S-N曲线。


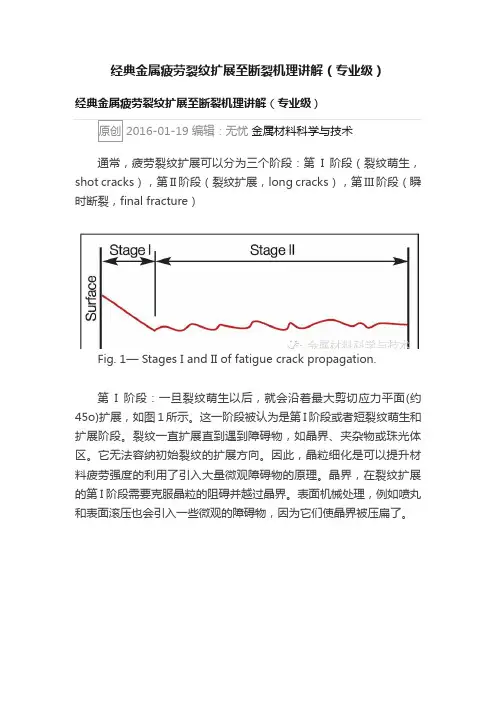
经典金属疲劳裂纹扩展至断裂机理讲解(专业级)经典金属疲劳裂纹扩展至断裂机理讲解(专业级)通常,疲劳裂纹扩展可以分为三个阶段:第I阶段(裂纹萌生,shot cracks),第II阶段(裂纹扩展,long cracks),第III阶段(瞬时断裂,final fracture)Fig. 1— Stages I and II of fatigue crack propagation.第I阶段:一旦裂纹萌生以后,就会沿着最大剪切应力平面(约45o)扩展,如图1所示。
这一阶段被认为是第I阶段或者短裂纹萌生和扩展阶段。
裂纹一直扩展直到遇到障碍物,如晶界、夹杂物或珠光体区。
它无法容纳初始裂纹的扩展方向。
因此,晶粒细化是可以提升材料疲劳强度的利用了引入大量微观障碍物的原理。
晶界,在裂纹扩展的第I阶段需要克服晶粒的阻碍并越过晶界。
表面机械处理,例如喷丸和表面滚压也会引入一些微观的障碍物,因为它们使晶界被压扁了。
Fig. 2 — Fatigue striations in (a) interstitial free steel and (b)aluminum alloy AA2024-T42. Figure (c) shows the fatigue fracture surface of a cast aluminum alloy, where a fatigue crack was nucleated from a casting defect, presenting solidification dendrites on the surface; fatigue striations are indicated by the arrow, on the top right side.第II阶段:由于裂纹扩展,实际载荷的上升,应力强度因子K不断增加,在裂纹尖端附近的不同平面上开始发生滑移,于是就进入了第II阶段。
第十四讲疲劳裂纹扩展上节回顾Dugdale模型(带状屈服模型)裂纹尖端张开位移(COD)无限大板的COD,有限宽板的CODCOD准则J积分,J积分的守恒性,J积分准则平面应力断裂的R阻力曲线1.疲劳裂纹扩展速率疲劳裂纹扩展的定量表示用da/dN,称为裂纹扩展速率,表示每个循环裂纹长度的平均增量。
da/dN-ΔK曲线与S-N、ε-N曲线类似,描述疲劳裂纹扩展规律的曲线为da/dN-ΔK曲线只有在拉伸应力作用下裂纹才能扩展,则疲劳裂纹应力强度因子幅度定义为ΔK = K max-K min R > 0ΔK = K max R < 0基本da/dN-ΔK曲线:R = 0的da/dN-ΔK曲线双对数坐标下da/dN-ΔK曲线的形状疲劳裂纹扩展的三个区域Array一般情况下,da/dN-ΔK曲线在双对数坐标上可分为三个区域1区:低速率区,该区内ΔK的微小降低,da/dN急剧下降。
存在ΔK的一个下限值ΔK th,该值处裂纹扩展速率近似为零,ΔK th称为门槛值。
ΔK th受R的影响较大。
2区:中速裂纹扩展区,裂纹扩展速率一般在10-9~10-5m/C范围内。
中速裂纹扩展区的da/dN-ΔK在双对数坐标上近似为线性关系。
3区:高速扩展区,即K max K C时,裂纹快速扩展,其寿命通常不考虑。
其上限值以铅垂渐近线表示2.裂纹扩展速率公式1)低速率区一般是进行裂纹不扩展设计ΔK < ΔK th2)中速裂纹扩展区,Paris公式Paris 对具有中心穿透裂纹平板拉伸实验数据归纳, 对中速裂纹扩展区(2区)提出的经验关系式m K C dNda)(∆= C ,m :材料常数m 不随构件的形状和荷载性质(拉伸或弯曲)改变,C 与材料性能相关。
由于存在门槛值ΔKth ,Donahue 等(Donahue ,1972)建议如下修正公式m th K K C dNda)(∆-∆= 3)高速扩展区可由下式估计裂纹扩展速率从2区向3区转变的应力强度因子 ys T E K σ00637.0max =K maxT :R = 0时的最大循环应力作用下的应力强度因子3.da /dN 的理论公式 塑性钝化模型C. Laird (1967)的观测结果裂纹尖端载循环荷载下出现反复钝化和 重新尖锐化的交替过程。
机械零件的疲劳裂纹扩展与寿命预测机械零件的疲劳裂纹扩展与寿命预测是材料科学和工程领域中的一项重要研究内容。
机械零件在运行过程中,由于受到载荷作用和材料本身的缺陷等原因,容易产生疲劳裂纹。
疲劳裂纹的扩展会导致零件的强度逐渐下降,最终导致零件的失效。
因此,了解疲劳裂纹的扩展规律以及预测零件的寿命对于确保机械设备的可靠性和安全性至关重要。
疲劳裂纹扩展是指在连续循环加载下,起初微小的裂纹随着时间的推移逐渐扩展。
疲劳裂纹扩展的速率与裂纹长度、应力幅、材料性能等因素密切相关。
通过对这些因素的研究,科学家们发现了裂纹扩展速率与裂纹尖端应力强度因子之间的关系。
应力强度因子是描述裂纹尖端应力集中程度的物理量,研究其变化规律对理解和预测裂纹扩展至关重要。
为了预测机械零件的寿命,研究者们发展了一系列的疲劳寿命预测模型。
其中最为常用的是基于裂纹扩展速率的模型。
该模型通过测定材料的疲劳裂纹扩展速率,结合裂纹的初始长度,预测零件的寿命。
这种寿命预测模型在实际工程中应用广泛且经验丰富。
除了裂纹扩展速率模型外,还有一些更为精确和复杂的寿命预测方法正在逐渐发展。
例如,基于有限元分析的寿命预测方法能够更加准确地模拟裂纹扩展过程,并预测零件的寿命。
这种方法考虑了零件在运行过程中的应力分布、应力集中情况等因素,能够更好地揭示裂纹扩展的机理。
然而,这种方法需要大量的计算资源和时间,适用范围相对较窄。
疲劳裂纹扩展与寿命预测的研究具有重要的实际应用价值。
通过理解裂纹扩展的机理和规律,工程师们可以设计更加可靠和寿命长久的机械零件。
对于一些关键部件,如飞机发动机叶片和汽车发动机曲轴等,预测其寿命至关重要,以保障设备的安全和稳定运行。
除了工程应用外,对于材料科学和力学领域的研究人员而言,疲劳裂纹扩展与寿命预测是提高材料性能和开发新型材料的重要途径之一。
通过深入研究疲劳裂纹扩展机理,科学家们可以设计出更好的材料,改善机械零件的使用寿命和可靠性。
此外,对材料的疲劳行为进行预测也有利于降低工程成本和能源消耗,从而实现可持续发展的目标。
机械结构的疲劳裂纹扩展特性分析与优化概述:机械结构的疲劳裂纹扩展特性是工程设计和使用过程中必须要考虑的重要问题之一。
疲劳裂纹扩展会导致结构强度下降,甚至引起严重事故。
因此,对机械结构的疲劳裂纹扩展特性进行深入分析和优化是至关重要的。
疲劳裂纹扩展的基本理论:疲劳裂纹扩展是指材料内部或表面的裂纹在受到交变载荷作用时逐渐扩展,在终止于结构破裂之前的过程。
裂纹扩展主要受到应力水平、载荷频率、环境条件以及材料的力学性能等因素的影响。
根据线弹性断裂力学理论,裂纹扩展速率可以用裂纹尖端位移增量和应力强度因子之间的关系来描述。
疲劳裂纹扩展的影响因素:1. 应力水平:应力水平是疲劳裂纹扩展的重要因素之一。
较高的应力水平会加速裂纹扩展过程,而较低的应力水平则会减缓裂纹扩展。
2. 载荷频率:载荷频率是指材料在受到交变载荷作用时的频率。
高频率下的载荷会加速裂纹扩展速度,而低频率下的载荷则会减缓裂纹扩展。
3. 环境条件:环境条件包括温度、湿度、腐蚀介质等因素。
某些环境条件下,如高温、高湿等,会导致材料的腐蚀和渗透,从而加速裂纹扩展。
4. 材料的力学性能:材料的强度、韧性和断裂韧性等力学性能会影响疲劳裂纹扩展的速率和路径。
疲劳裂纹扩展分析方法:1. 线性弹性断裂力学法:该方法假设材料具有线弹性行为,在结构的局部区域进行裂纹尖端位移和应力强度因子的计算。
2. 塑性力学法:该方法考虑材料的塑性行为,将材料的强度和塑性变形考虑在内,从而可以更准确地计算裂纹尖端位移和应力强度因子。
3. 数值模拟方法:数值模拟方法通过建立有限元分析模型,利用计算机进行裂纹扩展过程的模拟,得到裂纹尖端位移和应力强度因子。
疲劳裂纹扩展优化方法:1. 结构优化:通过改变结构的几何形状和尺寸,减少应力集中和应力激励,从而减缓裂纹扩展速率。
2. 材料优化:选择具有较高强度、韧性和断裂韧性的材料,可以增加结构的抵抗裂纹扩展的能力。
3. 加工和热处理优化:通过合理的加工和热处理工艺,降低材料中的缺陷和应力,减少裂纹扩展的可能性。
疲劳裂纹扩展的基本规律及其主要的影响因素疲劳是指在交变应力作用下发生在材料或结构某点局部、永久性的损伤递增过程。
疲劳在自然界和工程上比较普遍。
在金属结构的失效形式里,疲劳断裂是一种主要形式,约占失效结构的90%,而疲劳断裂是由于金属结构在循环载荷的作用下,由于各种原因(如应力集中等),引起疲劳强度降低而产生裂纹,最终由裂纹的扩展而导致结构失效。
疲劳裂纹扩展的规律疲劳裂纹在扩展过程中一般可分为三个阶段:近门槛值阶段、高速扩展阶段(Paris区)和最终断裂阶段。
在近门槛扩展阶段,疲劳裂纹的扩展速率很小,疲劳裂纹扩展速率随着应力强度因子范围△K的降低而迅速下降,直至da/dN→0,与此对应的△K值称为疲劳裂纹扩展门槛值,记为△K;在Paris区,疲劳裂纹扩展速率可以用Paris公式来定量地进行描述。
其中,C和m是试验确定的常数。
在高速扩展区,随着△K的提高,裂纹扩展速率升高,当疲劳循环的最大应力强度因子Kmax接近材料的Kic时,裂纹扩展速率急剧增加,最终导致构件断裂。
疲劳裂纹扩展一般由疲劳裂纹扩展速率da/dN表征,即在疲劳载荷作用下,裂纹长度a随循环次数N的变化率,反映裂纹扩展的快慢。
疲劳裂纹扩展速率da/dN的控制参量是应力强度因子幅度△K,表示材料的疲劳性能。
研究疲劳裂纹的扩展规律一般通过两种途径:一是过实验室观察,根据实验结果直接总结出裂纹扩展规律的经验公式;二是结合微观实验研究提出裂纹扩展机理的假设模型,推导出裂纹扩展规律的理论公式。
疲劳裂纹扩展规律的研究,主要是寻求裂纹扩展速率da/dN与各有关参量之间的关系。
疲劳裂纹扩展影响因素1. 残余应力对疲劳裂纹扩展的影响(1) 残余应力模型认为,在加载过程中裂纹张开,裂纹尖端附近形成一个塑性区,载荷峰值越大,则塑性区尺寸就越大:卸载后,由于塑性区周围的弹性区材料要恢复原来的尺寸,为了保持变形协调,已产生了永久变形的塑性区内的材料就要受到周围弹性区的压缩而产生残余压应力。
第五章疲劳裂纹扩展§5.1 概述前面介绍的内容为静载荷作用下的断裂准则。
构件在交变应力作用下产生的破坏为疲劳破坏,疲劳破坏的应力远比静载应力低。
一、疲劳破坏的过程1)裂纹成核阶段交变应力→滑移→金属的挤出和挤入→形成微裂纹的核(一般出现于零件表面)。
2)微观裂纹扩展阶段微裂纹沿滑移面扩展,这个面是与正应力轴成45°的剪应力作用面,是许沿滑移带的裂纹,此阶段裂纹的扩展速率是缓慢的,一般为10-5mm每循环,裂纹尺寸<0.05mm。
3)宏观裂纹扩展阶段裂纹扩展方向与拉应力垂直,为单一裂纹扩展,裂纹尺寸从0.05mm扩展至临a,扩展速率为10-3mm每循环。
界尺寸c4)断裂阶段a时,产生失稳而很快断裂。
当裂纹扩展至临界尺寸c工程上一般规定:①0.1mm~0.2mm裂纹为宏观裂纹;②0.2mm~0.5mm,深0.15mm表面裂纹为宏观裂纹。
N)宏观裂纹扩展阶段对应的循环因数——裂纹扩展寿命。
(pN)以前阶段对应的循环因数——裂纹形成寿命。
(i二、高周疲劳和低周疲劳高周疲劳:当构件所受的应力较低,疲劳裂纹在弹性区内扩展,裂纹的疲劳寿命较长。
(应力疲劳)低周疲劳:当构件所受的局部应力已超过屈服极限,形成较大的塑性区,裂纹在塑性区中扩展,裂纹的疲劳寿命较小。
(应变疲劳)工程中一般规定N≤105为低周疲劳。
f三、构件的疲劳设计1、总寿命法测定S-N曲线(S为交变应力,N为应力循环周次)。
经典的疲劳设计方法是循环应力范围(S-N)曲线法或塑性总应变法来描述导致疲劳破坏的总寿命。
在这些方法中通过控制应力幅或应变幅来获得初始无裂纹的实验室试样产生疲劳破坏所需的应力循环数和应变循环数。
N=Ni +Np(Ni萌生寿命,Np扩展寿命)2、损伤容限法(疲劳设计的断裂力学方法)容许构件在使用期内出现裂纹,但必须具有足够的裂纹亚临界扩展寿命,以保证在使用期内裂纹不会失稳扩展而导致构件破坏。
疲劳寿命定义为从某一裂纹尺寸扩展至临界尺寸的裂纹循环数。
§5.2应力疲劳条件下裂纹扩展速率一、疲劳裂纹扩展速率的概念裂纹扩展速率:如果在应力循环N ∆次后裂纹扩展为a ∆,则应力每循环一次裂纹扩展量为a N ∆∆(mm/次),称为裂纹扩展速率。
在极限条件下用微分da dN 表示。
在单轴循环交变应力下,垂直于应力方向的裂纹扩展速率,一般可写成如下形式:(),,c daf a c dNσ= 其中:N -应力循环次数σ-正应力a-裂纹长度c -与材料有关的常数研究疲劳裂纹扩展速率的概念的重要性:计算裂纹体的剩余寿命。
例:已知瞬时裂纹扩展速率dadN初始裂纹的长度0a ,临界裂纹的长度c a ,→裂纹扩展至断裂的循环次数:ca p a da N da dN=⎰研究疲劳裂纹的扩展规律一般通过两种途径:⑴通过实验室观察,根据实验结果直接总结出裂纹扩展规律的经验公式; ⑵结合微观实验研究提出裂纹扩展机理的假设模型,推导出裂纹扩展规律的理论公式。
二、疲劳裂纹扩展的经验公式Paris 应力强度因子理论与实验结果符合较好。
高周疲劳(应力疲劳)裂纹尖端塑性区的尺寸远小于裂纹长度,近似为线弹性断裂力学问题。
在线弹性断裂力学范围内,应力强度因子能恰当描述裂纹尖端的应力场强度→应力强度因子K 是控制dadN 的主要参量。
即dadN与应力强度因子幅值K ∆存在一定的函数关系,K ∆为由交变应力最大值max σ和最小值min σ所计算的应力强度因子之差,即max min K K K ∆=- (max max K σ→,min min K σ→)一般情况,daKdN -∆关系曲线在双对数坐标系内分为三阶段:第一阶段:K I ∆很低,当th K K I ∆<∆时,裂纹基本不扩展,th K ∆称为门槛值th K ∆受循环特征R 的影响很大,min max K R K =对于马氏体钢,巴尔涩姆(Barsom )得出如下经验公式:6.4(10.85)5.5th R K -⎧∆=⎨⎩ 0.10.1R R >≤ 第二阶段(直线型)Paris (巴里斯)最早用实验得到这一关系。
实验:控制载荷(应力)、中心穿透裂纹的平板拉伸试验或三点弯曲试样做疲劳试验。
记录每隔一段时间的i a 及对应的i i i da dN N K ⎫⎛⎫⎪⎪⇒⇒⎝⎭⎬⎪∆⎭各瞬时的双对数坐标系内计算对应的 ⇒⇒在一定范围内是一条直线经验公式mda C K dNI =∆()(Paris 公式) 式中:C -材料常数,与材料的力学性质有关。
m -材料常数。
大量实验表明:m C AB =,其中:11()()200002500A =普通钢,铝合金,155B =。
第三阶段:当max IC K K →时,发生迅速断裂。
实际上存在上限值,fL K →疲劳断裂韧度,当.6fL thK K o ∆∆时,dadN 急速增加。
由max lim IC K K da dN →⎛⎫=∞ ⎪⎝⎭max 1K K RI∆=-,又min max ,K R K ⎛⎫= ⎪⎝⎭为循环特征()()max 110lim lim lim IC IC IC K K K R K K R K da da da dN dN dN I I →∆→-∆--→⎛⎫⎛⎫⎛⎫⇒===∞ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()11IC daR K K dN-I ⇒--∆⇒⎡⎤⎣⎦具有的奇异性富尔曼(Foreman )公式()()1mIC C K da dN R K K I I∆=--∆⇒材料的断裂韧度和循环特征对疲劳裂纹扩展速率的影响。
§5.3影响疲劳裂纹扩展速率的因素通过实验观察:平均应力、应力条件、加载频率、温度、环境等对dadN 均有影响。
一、平均应力的影响⑴在同一K ∆下,平均应力越高,dadN 越大。
max min212m R σσσσσ+∆∆==--其中,min minmax max K R K σσ==,为循环特征(应力比)m daR dNσ⇒对的影响体现的影响。
由Foreman 公式:()()1mIC C K da dN R K K I I∆=--∆,dadN⇒R 增加增加。
(2)大量实验表明:th th daR K R K dN⇒∆∆不仅影响,而且影响,一般随增加,减小。
经验公式:()1mth th K K R ︒∆∆-=其中:00.5~0.9th K R m ︒∆==是的门槛值,一般。
工业上用到这一性质提高寿命。
得到:平均应力为压应力,相比于拉应力或为零的情况,dadN降低,th K∆上升,提高疲劳寿命。
这一特性的应用:高压容器→自增强处理航空零部件→表面的喷丸处理→形成表面残余压应力。
二、超载的影响过载峰对后面的低载恒幅下的裂纹扩展速度有延缓的作用,延缓作用限于一定的循环周期,以后dadN 逐渐恢复正常。
+ =σσt tt =tt t1、惠累尔(Wheeler )模型认为:过载峰使裂纹尖端形成大塑性区*R ,而塑性区*R 阻碍裂纹增长,使裂纹产生停滞效应。
若在恒定的下裂纹扩展速率为()mda C K dN I =∆用于大塑性区而延缓的裂纹扩展速率()mpi daC C K dNI =∆延缓其中:pi C 反映停滞效应的延缓参数,取值0-1。
,1,ay pi p R C a a ⎧⎛⎫⎪ ⎪ ⎪=-⎨⎝⎭⎪⎩y py p a R a a R a +<+>:y R 其中:恒定引起的塑性区。
p a :弹性区与塑性区的交界面的位置。
:n 形状参数。
2、埃尔伯(Elber )模型tN认为:超载后裂纹的闭合效应,使裂纹的扩展速率降低。
当施加过载峰时,裂纹尖端产生较大的残余拉应变,过载峰后,在随后的恒定K ∆作用下逐渐卸载过程中,因裂尖已形成残余拉应变,使裂纹尖端过早闭合,→裂纹的闭合效应→裂纹尖端实际的应力强度因子eff K ∆比实际外加值K I ∆小→延缓裂纹扩展速率。
eff K U K ∆=∆埃尔伯:max max minop U σσσσ-=-其中:式中:op σ裂纹开始张开应力。
()meff da C K dN⇒=∆延缓三、加载频率的影响1、加载频率减小,裂纹扩展速率增加,但随K ∆的减小,其影响逐渐减少。
2、高温下,加载频率对裂纹扩展速率的影响大些,在K ∆某转折点之内,加载频率越低,dadN 越高。
大量实验表明:(1)当K ∆较低时,dadN 基本不受频率的影响。
(2)当K ∆较大时,加载频率有较大影响。
加载频率降低,dadN 增高。
加载频率增高,dadN 降低。
()()mda f K dN⇒∆=A ()f f 其中:A 是加载频率的函数。
四、温度的影响用于核反应堆压力容器的304不锈钢,温度从24℃增加到650℃,dadN 随之增加。
阿汉纽斯(Arrhcnius )公式:()u K dadN RT ∆⎡⎤-⎢⎥⎣⎦=Aexp 式中:A-常数()u K ∆-激活能R-玻耳兹曼常量 T-绝对温度大量实验表明:(1)对于大多数材料,随温度的升高,dadN 增高。
(2)随dadN 的增高,温度对da dN 的影响减弱。
五、其他影响因素1、腐蚀介质明显提高dadN2、随机加载的影响在相同的max min m σσσ、、下随机加载的da dN 高,而实验室的程序加载dadN 低。
但随着dadN 的增加这种影响减小。
用实验室简单的程序加载得出的结论应用于随机加载情况计算是危险的。
低周疲劳:构件的槽底或拐角等处。
1、裂纹扩展速率Paris 公式:()mda C K dN ∆= 塑性区的裂纹扩展速率⑴J 积分表达式:ndaCJ dN =J J -其中:积分, C,n 为材料常数。
应变幅度表达式:()nda C dN ε∆=ε∆-其中:总应变幅,C,n 为材料常数。
⑵构件的剩余寿命 裂纹的扩展因数为:c a p a dada dN =⎰N使用年限内裂纹的扩展量:Ndaa dN dN∆=⎰其中:N-使用年限内的循环次数。
一般规定:交变载荷:启动→正常运转→停机为一次循环,工作年限内采用1000次循环计算。
⑶裂纹的形成寿命f i p N =N +Na p i N C ε∆=p a c ε∆-其中:塑性应变幅,、为材料常数。
e eεε∆∆=∆局部应变幅的计算:K e -其中:K 塑性应变集中系数e ∆-名义应变幅度p e εεε⇒∆=∆-∆ e E σε∆∆=注意:低周疲劳应考虑蠕变影响。
六、小结(1)与传统的疲劳极限相比,断裂力学中也存在一个极限值,th K ∆(门槛值),当th K K ∆<∆时不扩展。
(2)加速dadN 的因素:正平均应力、随机加载方式、温度、低频率减缓dadN 的因素:负平均应力、过载峰、高频率(3)除频率因素外,上述各因素对da dN 较小时影响显著,在dadN 较大时影响较小。