11菱形的性质与判定(2)2

第一章特殊平行四边形1. 菱形的性质与判定（2）一、学情与教材分析1.学情分析上节课，学生已经经历了独立探索发现菱形性质的过程，通过折纸等活动学生体会了“实验—猜想—证明—应用”的科学探索过程，认识了菱形与平行四边形的关系，这些都为本节课进一步探索和发现菱形的判定定理提供了较好的知识基础和活动经验基础。

2.教材分析本节课，学生将探究菱形的判定定理，应该说，有了上节课的铺垫，本节课可以更多地让学生自主探索。

第一个定理的证明中，需要首先明确判定定理与性质定理的关系，这样为后面一系列定理的证明打下基础；第二个定理教科书中是通过设置一个尺规作图的问题引入的，在学生自行完成尺规作图并明确了作法的可行性后，引导学生自主完成证明过程。

本节课中将通过学生的自主证明过程，提升学生的逻辑推理能力，通过经历尺规作菱形提升学生的动手操作能力和规范的语言表达能力.二、教学目标1.经历菱形的判定定理的探究及证明过程及其运用；2.掌握用尺规作菱形的方法；3.经历“探索——猜想——证明”的学习过程，进一步提高推理论证的能力.三、教学重难点重点：菱形判定定理的证明和应用.难点：通过尺规作图法作菱形.四、教法建议采用“展示交流——合作论证——知识运用（训练提升）”的教学模式，引导学生观察、思考、讨论、总结并形成结论，让学生在探究中体会所学知识.五、教学过程（一）课前设计1.预习任务：任务1：制作菱形①在一张纸上用尺规作图做出边长为10cm的菱形；②想办法用一张长方形纸剪折出一个菱形.③利用长方形纸你还能想到哪些制作菱形的方法.任务2：怎样去判定一个四边形是菱形呢菱形性质定理的逆命题是不是可以作为判定定理呢请回答下列问题：①：菱形的四条边相等的逆命题是什么②：①中的两个逆命题是否正确请尝试证明！对于不正确的命题请添加适当的条件，使它成立.2.预习自测：一、填空题1.如图，如果要是平行四边形是一个菱形，需要添加一个条件，那么你添加的条件是________________.B答案：AB=BC，或AC⊥BD（答案不唯一）解析：由定义知，当AB=BC时，平行四边形ABCD是一个菱形；由判定定理知道，当AC⊥BD时，平行四边形ABCD是一个菱形，所以两个答案都可以.点拨：熟练掌握菱形的判定方法即可解答此题.2.如图，等边△ABC中，点D,E,F分别是AB,BC,AC边上的中点，则图中有________个菱形.CB答案：3解析：∵△ABC是等边三角形，∴AB=AC=BC ，∵D 、E 、F 分别是AB 、BC 、CA 边上的中点，∴DF=12BC ，DE=12AC ，EF=12AB ， ∴DF=EF=ED=AD=AF=CF=CE=BE=BD ，∴有3个菱形：菱形ADEF ，菱形BDFE ，菱形CFDE ．故答案为3．B点拨：根据等边三角形和中位线的性质可得DF=EF=ED=AD=AF=CF=CE=BE=BD . 再根据菱形的判定定理即可解答此题3.如图，在等腰梯形ABCD 中，AB 添加一个你认为合适的条件_______________，使四边形AECD 为菱形.E A 答案：AD ∵AD=CD ，∴四边形AECD 为菱形.当AD=AE ，∵AD=CD ，∴AE=CD. 又∵AB ∴四边形AECD 为菱形.当∠CEB=∠B ； ∵等腰梯形中，∠A=∠B ，∴∠A=∠CEB.∴AD 又∵AB ∴四边形AECD 为菱形.点拨：利用平行四边形和菱形的判定定理，先证平行四边形，再证菱形.（二）课堂设计1、知识回顾C 图1—1内容：通过练习复习上节课所探究的菱形的性质.1)菱形ABCD中，AC=8，BD=6，则菱形的周长是______2)如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC与点F,垂足为点E，连接DF,则∠CDF等于________设计意图：通过课件中的问题回顾上节课探究过的菱形的性质定理，从而为本节课的继续探究，尤其是理论证明做铺垫。

菱形的性质与判定菱形是一种具有特殊性质的四边形，它的对角线长度相等，且相交于垂直的交点。

在几何学中，我们可以通过一些准确的判定方法来确定一个四边形是否为菱形。

本文将介绍菱形的性质，并详细探讨判定菱形的几种方法。

一、菱形的性质1. 对角线相等：菱形的两条对角线长度相等，即AC=BD。

这是菱形的最基本特征。

2. 对角线相交垂直：菱形的两条对角线相交于一个垂直的交点。

换句话说，∠ACD和∠BCD是两条相交直线上的垂直角。

3. 对边平行：菱形的两对边互相平行，即AB║CD且AD║BC。

4. 具有四个等边角：菱形的四个内角均相等，每个角度为90度。

二、判定菱形的方法1. 利用对角线相等判定：如果一个四边形的两条对角线相等，那么它就是一个菱形。

例如：已知一个四边形ABCD，我们可以测量AC和BD的长度，如果AC=BD，那么我们可以确定该四边形是一个菱形。

2. 利用对边平行判定：如果一个四边形的两对边互相平行，那么它就是一个菱形。

例如：已知一个四边形ABCD，我们可以测量AB、BC、CD、DA的长度，并检查相邻边是否平行。

如果AB║CD且AD║BC，那么可以确认该四边形是一个菱形。

3. 利用角度特征判定：如果一个四边形的四个内角均为90度，那么它就是一个菱形。

例如：已知一个四边形ABCD，我们可以测量∠ABC、∠BCD、∠CDA和∠DAB的度数，如果每个角度都等于90度，那么可以断定该四边形是一个菱形。

以上三种方法可以独立或结合使用，来判定一个四边形是否为菱形。

在实际问题中，根据提供的信息，我们可以选择最适合的方法进行判定。

值得注意的是，只满足菱形的一些性质，比如对角线相等，不一定就能判定一个四边形是菱形。

必须满足菱形的所有性质才能确定。

三、菱形的应用菱形在几何学中有很多应用，以下列举几个常见的应用：1. 菱形判断：在解决几何问题时，判定一个四边形是否为菱形可以帮助我们简化推理过程，节省解题时间。

2. 菱形面积计算：菱形的面积计算公式为S=a×b/2，其中a和b分别表示菱形的对角线长度。

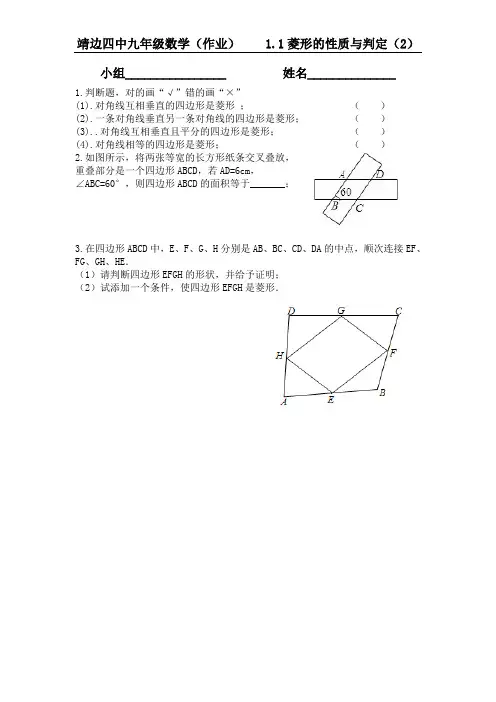
小组________________ 姓名______________
1.判断题，对的画“√”错的画“×”
(1).对角线互相垂直的四边形是菱形；（）
(2).一条对角线垂直另一条对角线的四边形是菱形；（）
(3)..对角线互相垂直且平分的四边形是菱形；（）
(4).对角线相等的四边形是菱形；（）
2.如图所示，将两张等宽的长方形纸条交叉叠放，
重叠部分是一个四边形ABCD，若AD=6cm，
∠ABC=60°，则四边形ABCD的面积等于_______；
3.在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，顺次连接EF、FG、GH、HE．
（1）请判断四边形EFGH的形状，并给予证明；
（2）试添加一个条件，使四边形EFGH是菱形．
3.如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．
(1)求证：四边形AECD是菱形；
(2)若点E是AB的中点，试判断△ABC的形状，并说明理由．
A
E
D
B C。

北师大九年级数学上 第三章 证明（三）一、温故互查：（二人小组互述）1. 菱形的定义是什么？2．平行四边形的判定方法有哪些？二、设问导读：阅读教材P 5-7完成下列问题：1.从“菱形的定义”中可知，要判定一个四边形菱形，首先要判定这个图形是__________四边形，再从边的角度考虑需满足条件_________________.2.将菱形的判定定理“对角线互相垂直的平行四边形是菱形”用数学符号语言表示为(对照教材图1—3)∵_____________________________ _____________________________ ∴四边形ABCD 是__________.3.教材中小颖的折纸方法利用了菱形的哪种判定方法？你还有其它的制作方法吗？ 4．已知：如教材图1—4，AB=BC=CD=AD. 求证：四边形ABCD 是菱形5.“例2”中，已知四边形ABCD 是平行四边形，再具备什么条件就可以成为菱形呢？这个条件是怎么找到的？三、自学检测：1.用两个全等的等边三角形，可以拼成下列哪种图形（ ）A ．矩形B ．菱形C ．正方形D ．等腰梯形2.如图，下列条件之一能使平行四边形ABCD 是菱形的为（ ）①AC ⊥BD ；②∠BAD=90°； ③AB=BC ； ④AC=BD ． A ．①③ B ．②③ C ．③④ D ．①②③3.如图，四边形ABCD 的对角线互相平分，要使它变为菱形，需要添加的条件是 _________ （只填一个你认为正确的即可）．1.2 菱形的性质与判定北师大九年级数学上 第一章 特殊平行四边形四、巩固训练：1.如图所示，将一个长为10cm ，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线） 剪下，再打开，得到的菱形的面积为________。

2.如图，已知点D 在△ABC 的BC 边上，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ． （1）求证：AE=DF ；（2）若AD 平分∠BAC ，试判断四边形AEDF 的形状，并说明理由．3.已知：如图，平行四边形ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别相交于点E 、F ．求证：四边形AFCE 是菱形．五、拓展探究：1．如图所示，在平行四边形ABCD 中，AE 是BC 边上的高，将△ABE 沿BC 方向平移，使点E 与点C 重合，得△GFC ． （1）求证：BE=DG ； （2）若∠B=60°，当AB 与BC 满足什么数量关系时，四边形ABFC 是菱形？证明你的结论．2.如图，等边△ABC 的边长为2，E 是边BC 上的动点，EF ∥AC 交边AB 于点F ，在边AC 上取一点P ，使PE=EB ，连接FP ． （1）请直接写出图中与线段EF 相等的两条线段；（不再另外添加辅助线） （2）探究：当点E 在什么位置时，四边形EFPC 是平行四边形？并判断四边形EFPC 是什么特殊的平行四边形，请说明理由。