当前位置：文档之家 › 大学物理电磁学部分07电介质的极化和介质中的高斯定理

大学物理电磁学部分07电介质的极化和介质中的高斯定理

  • 格式：ppt
  • 大小：347.58 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

介质的极化和介质中的高斯定理

介质的极化和介质中的高斯定理


部电都介产质生内附部加的电总场场E强'。E
E0
E'
E0
'
'
极化电荷所产生的附加电场不足以将介质中的外电
场完全抵消，它只能削弱外电场。称为退极化场。
介质内部的总场强不为零！ 在各向同性均匀电介质中： E
E0
r
r称为相对介电常数或电容率。
3
二、介质中的高斯定理 电位移矢量
1.介质中的高斯定理
d
D2S 0S D1 D2 0 , D2 0
E2
D2
0r
0 0r
11
I区：D1
0,
E1
0 0
0
II区：D2 0 ,
②.求电容C
E2
0 0r
由C q U ab
与 U ab
Ed
高 斯
C q
0S
面
U ab E1(d d ' ) E 2d '
d' 0
D P1 P2
r
d
质中的高斯定理求场强：先根据自由电荷的分布利用 介质中的高斯定理求出电位移矢量的分布，再根据电 位移矢量与场强的关系求出场强的分布。
7
例1：将电荷 q 放置于半径为 R 相对电容率为 r 的介
质球中心，求：I 区、II区的 D、E、 及 U。
解：在介质球内、外各作半径为 r 的
高斯球面。
SD dS q0
荷密度为 0 , 其间插有厚度为 d’ 、电容率为 r 的电介质。
求 ： ①. P1 、P2点的场强E；②.电容器的电容。
解： ①. 过 P1 点作高斯柱面, 左右底面分别经过导体
和 P1 点。
D SD dS q0
介质中的高斯定理

介质中的高斯定理

1 ' 0 1 r ' 0, r 1 ' 0 , r
真空中 导体中
结论3
P与E的关系
0 0 r 1 ( r 1 ) 0 E 0 r
令 r 1 为电极化率。
1 由 P ' 和 ' 0 1 r 0 1 P ' 0 1 r 1 r r
R2
εr2
εr1 R1
R
解：E 和D 的分布具有柱对称性
D dS D 2rl l
S
D ( R1 r R2 ) 2r D E1 ( R1 r R ) 0 r1 20 r1r
D E2 0 r 2 20 r 2 r ( R r R2 )
P 0E
结论4
无介质 充满介质
充满各向同性的均匀电介质的电容器
C0
0S
C rC0
A
B
d q0 C U AB
S
q0 q S q 0 0 r 0 C U AB Ed E0 0 d d r 0 r 0S rC0 d
d
平行板电容器为例
例11.9 真空中有一半径为R，带电量为q的金属 球壳。求： （1）电场的总能量； （2）带电球壳周围空间中，多大半径球面内的 电场所具有的能量等于总能量的一半。


q
p
q
E0
E0 F
F
在介质表面产生极化电荷。
三、极化强度 描写电介质极化程度的物理量。 定义：单位体积内的电偶极矩矢量和。
p P V
E0
注意
1.真空中 P = 0 ，真空中无电介质。
大学物理介质中的高斯定理

大学物理介质中的高斯定理


r1
r2
18
例:球形电容器由半径为R1的球体和内半径为R3的导 体球壳构成，带电 q，其间有两层均匀电介质，
分界面的半径为R2，相对介电常数分别为r1和r2 。 求：E, D 和C。
解：
D

dS

4
r
2

D

q
S
R2
R1 r2
D1

q 4r 2
D2

q 4r 2
R3
r1
在界面上电位移线会发生折射
tan1 1
tan2
2
2 1
若 2 > 1 2 > 1 ，电位移线将折离法线
*
上海交通大学 董占海
28
证明：
E1t E2t D1n D2n
E1sin1 E2sin2
D1 cos 1 D2 cos 2
D1 1E1 D2 2 E2
39
思考：带电金属球 (R、Q)，半个球处在电介质εr 中，则球正下方r > R 处的 E、D。
r
同上
上海交通大学 董占海
40
例5：一点电荷Q放在半无限大电介质为εr和真空的 界面处，求E、D。
解：空间的场强 = 两个点
电荷Q和q′产生的
故空间各点的E、为
r
点电荷的场，具有球
对称性
xd 2
2 DS 0 0 S0d
D

i
0
d
2
上海交通大学 董占海
d


r
0
Ox
23
xd 2
E

D
0r

0 x
第七节 有电介质时的高斯定理

第七节 有电介质时的高斯定理


3
第七节 有电介质时的高斯定理
1. 有极分子和无极分子
电介质
无极分子：（氢、甲烷、石蜡等）
有极分子：（水、有机玻璃等）
有极分子— 极性电介质
特点：分子正负电重心不重合，有固有电偶极矩；
4
第七节 有电介质时的高斯定理
无极分子 — 非极性电介质 例如 H2、O2、CO2、CH4
特点：分子正负电中心重合，无固有电偶极
布求得合场强的分布。
11
第七节 有电介质时的高斯定理
例 7-13 设一带电量为Q 的点电荷周围充满电容率 为 的均匀介质，求场强分布。 解： 根据介质中的高斯定理
2 D ds D 4 r q0
S
r
q0 D 4 r 2
1 q0 E 2 4 r D
8
第七节 有电介质时的高斯定理
（2）有电介质时的高斯定理
1 SE dS ε0 (Q0 Q)
Q0 由 εr Q0 - Q
Q0
Q
Q0 得 E dS S ε0 ε r

S
0 r E dS Q0
9
第七节 有电介质时的高斯定理

S
0 r E dS Q0
S
D 2 π rl l
D

2πr


D E ε0 ε r 2 π ε0 ε r r
( R1 r R2 )
R2
r
R1
14
第七章 静电场
一 电介质的极化
二 有电介质时的高斯定理
1
第七节 有电介质时的高斯定理
一、电介质的极化
电介质指的是导电性极差的物质。在电介质内 几乎不存在自由电子（或正离子）。通常条件下的
有电介质时的高斯定理

有电介质时的高斯定理

有电介质时的高斯定理
有电介质时的高斯定理是电学中的一个重要定理，它描述了电场的分布与电荷分布的关系。

此定理的公式表述为：电场穿过一个封闭曲面的通量等于该曲面内部的电荷总量的比例，即ΦE=Q/ε0，其中ΦE为电场的通量，Q为曲面内部的电荷总量，ε0为真空中的电介质常数。

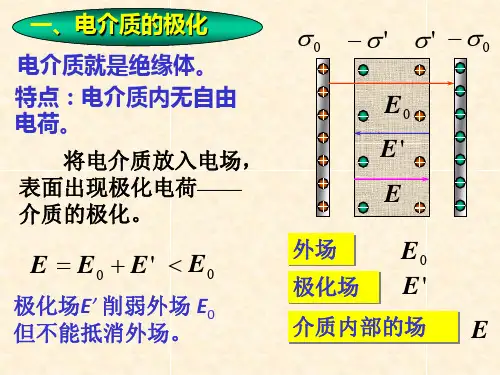
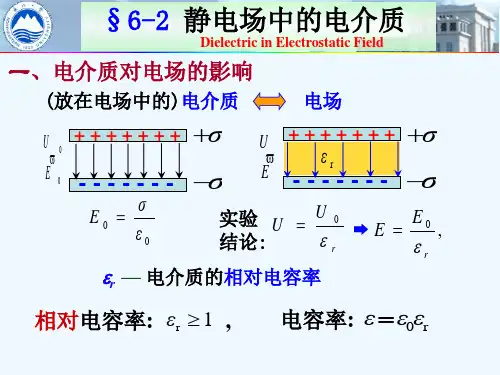
在有电介质时，电场的分布受到电介质的影响。

电介质的存在会使电场强度发生改变，这是因为电介质的分子会被电场极化，从而产生极化电荷。

这些极化电荷会改变电场的分布，使电场在电介质中的强度比在真空中的强度小。

因此，在有电介质时，要考虑电介质对电场的影响，才能准确地计算电荷的分布。

在应用高斯定理时，通常需要选择一个适当的曲面来计算电场的通量。

曲面的选择应当考虑到电荷分布的对称性，以便简化计算。

在有电介质时，曲面的选择也需要考虑到电介质的影响。

如果曲面穿过电介质，那么在计算电荷总量时，需要将电介质中的极化电荷也计算在内。

高斯定理的应用范围很广，包括电场的计算、电容器的设计、电荷分布的测量等。

在电场的计算中，高斯定理可以用来求解各种电场分布，例如电偶极子、均匀带电球面等。

在电容器的设计中，高斯定理可以用来计算电容器的电容量，从而确定电容器的电荷储存能
力。

在电荷分布的测量中，高斯定理可以用来测量电荷的总量，从而确定电荷的分布情况。

有电介质时的高斯定理是电学中的一个重要定理，它描述了电场的分布与电荷分布的关系。

在应用该定理时，需要考虑到电介质的影响，并选择适当的曲面来计算电场的通量。

高斯定理的应用范围很广，包括电场的计算、电容器的设计、电荷分布的测量等。

第四节电介质中的高斯定理

第四节电介质中的高斯定理

5电介质中高斯定理的应用应用电介质中的高斯定理可以很方便地求解电荷和电介质都对称分布时的电场的场强
《大学物理》
教师：
胡炳全
第四节
电介质中的高斯定理
1、推导 根据电介质中的电场只要考虑了 极化电荷就可以当成真空来处理 的基本思想。高斯定理可写为：
∫ E ⋅dS = ε
S
q内
0
P
E0
=
q0 − q '
ε0
S
由 : q' = − ∫ P ⋅ d S
S
∫ (ε
S
0
E + P ) ⋅ d S = q0
高斯定理可以重新写为：
令 : D = ε0 E + P
则有 : ∫ D ⋅ d S = q0
S
《大学物理》
教师：
胡炳全
2、电位移
D = ε0 E + P
叫电位移。它是一个矢量。它没 有直接的物理意义。
若电介质是线性极化的，则有：
S S S S
R2 ε Q r R1
= D 4πr = q0
2
Q r3 q0 = Q 3 R1
r > R1 r < R1
Q 4πr 2 D = Qr 4πR13
r > R1 r < R1
《大学物理》 根据
教师：
胡炳全
D =εE
ε 0 , r < R1 ε = ε , R1 < r < R2 ε , r>R 2 0 Qr 4πε R 3 , r < R1 0 Q , R1 < r < R2 E= 2 4πεr Q , r > R2 2 4πε 0 r
静电场7-电解质的极化,束缚电荷,电解质中的高斯定理,电位移矢量

静电场7-电解质的极化,束缚电荷,电解质中的高斯定理,电位移矢量

§10.9 电介质的极化束缚电荷
电偶极子. 一对相距为l 的等量异号点电荷，若从电荷连线的中点 向场点 P 画一位矢 r ，且满足： r >> l 的条件，则这一对 等量异号点电荷叫做电偶极子(electric dipole)。
定义电偶极矩 (electric moment)： p ql
S1


S1
A
1
S2 d1
2
B
D1 S1 S1
D1
同理，做一个圆柱形高斯面 S2 SD dS qi ( S 2内） D2
2
d2
D1 D 2
2014-4-12
E1 E 2
第十章 -- 静电场
西安电子科技大学
12
§8.9 电介质

E1 o r1
R1
E2
E1
R2
E1 2 .5 E 2
u
R 2 2 . 5 R1
R
R2
1
E dr
*
R
R2
1
R2 R1 E ln R1 E * ln 2 . 5 R1
2014-4-12
dr R1 E 2 0 r r
* R2
R
1
dr r
r
第十章 -- 静电场
d1
d2
西安电子科技大学
13
例 一单芯同轴电缆的中心为一半径为R1的金属导线，外层一金 属层。其中充有相对介电常数为r 的固体介质，当给电缆加 一电压后，E1 = 2.5E2 ，若介质最大安全电势梯度为E 求 电缆能承受的最大电压？ 解 用含介质的高斯定理 * E 2 R E 0 r 1 2 0 r r
电介质的高斯定理

电介质的高斯定理

电介质的高斯定理
高斯定理又称为电通量定理，是描述电场分布的一条基本定理，它是高斯定律的一部分。

高斯定理是指在电介质中，通过一个闭合曲面的电通量与该曲面所包围电荷的代数和成正比。

具体而言，电介质的高斯定理可以用如下公式表示：
∮E·dA = Q/ε
其中，∮E·dA表示通过闭合曲面的电场E与面元dA的点积之和，Q表示该闭合曲面所包围的电荷量，ε表示电介质的介电常数。

高斯定理表明，电场通过一个闭合曲面的总电通量与这个曲面所包围的总电荷成正比关系。

通过这个定理，可以方便地计算电场分布及电荷分布之间的关系。

在应用高斯定理时，需要注意以下几点：
1. 选择合适的闭合曲面：闭合曲面可以是球面、柱面、平面等等，具体的选择要根据实际情况来确定。

一般来说，如果电
荷分布比较对称，选择球面作为闭合曲面较为方便。

2. 计算电场通量：通过选择的闭合曲面计算电场与面元的点积之和，即计算∮E·dA。

这一步需要根据具体的电场分布来进行计算，可以利用库仑定律等来求解。

3. 计算电荷量：根据实际情况确定闭合曲面所包围的电荷量Q。

如果已知电荷分布，可以直接计算；如果未知，则需要根据已知的电场分布来进行推导。

4. 确定介电常数：介电常数ε是电介质的一个属性，它反映了电场在电介质中的传播速度和电荷分布的影响程度。

不同的介电常数对应不同的电介质材料，可以通过实验测量或者查找资料获得。

通过以上步骤，可以利用高斯定理计算电场的分布以及与电荷之间的关系。

高斯定理不仅适用于电介质，还可以用于真空中的电场分布计算，只是在真空中介电常数ε的值为真空介电常数ε0。

07电介质及其极化 介质中的高斯定理 电位移 静电场的能量

07电介质及其极化 介质中的高斯定理 电位移 静电场的能量


1D 1 1 2 V体 结果讨论：We E V体 EDV 体 2 2 2 •电容器所具有的能量与极板间电场 E 和 D 有关，E 和 D 是极板间每一点电场大小的物理量，所以能量与电场
存在的空间有关，电场携带了能量。
Fan
2
2
2
We 定义电场能量能量密度：w e V体
意义：单位体积内的电场能量。
2 1 2 1 1D w e E ED 2 2 2
•电容器所具有的能量还与极板间体积成正比，于是可 定义能量的体密度，它虽然是从电容器间有均匀场而 来但有其普遍性。
非均匀电场能量计算
We we dV
V
只要确定 we 就可计算电场能量 We。 Q2 1 2 W CU 强调：电容器的能量亦可由 e 计算。 2C 2
Fan
有极分子电介质：电介质中各分 子的等效正电中心与等效负电中 心不重合的电介质；正点中心和 负电中心分别可用等量异号电荷 代替，二者有一相对位移，这样 每个分子对外界的电性效果可以 等效为一个电偶极子的作用
H2O CO SO2
O 负电荷中心
Pe
+H 水分子 H 2O
+
Pe 0
+H 正电荷中心
0
A外 dA 0
Q
Q2 q dq C 2C
外力所作的功全部转化为储存于电容器中的电能。
Q2 We A外 2C
1 Q2 1 2 由 Q CU 有： We CU QU 2 2C 2
Q2 1 2 所以储存在电容器中的能量为： CU We 2C 2
Fan
r , 0 r 0
真空εr = 1 导体εr → ∞
介质中的高斯定理

介质中的高斯定理


v E
D
介质中的高斯定理
例 自由电荷面密度为0的平行板电容器，其极化电荷面密度
为多少？
解: 由介质中的高斯定理
-+´0
DS 0S D 0
D +´
E
D
0r
0 0 r
- 0
0 0
E0
0 0
E 0
E E0 E
0 r 0 0
1
1
r
0
E
dS S
++++++
-q - - - - - -
移出S面
qi
留在S面内
介质中的高斯定理
v v E dS
S
1
0
qi
1
0
vv P dS
S
S 0E P dS qi
定义电位移矢量: D 0 E P C m2
介质中的高斯定理: 在任何静电场中，通过任意闭合曲面 的电位移通量等于该曲面所包围的自由电荷的代数和.
D S
dS
qi
说明:
D S
dS
qi
介质中的高斯定理
1. 介质中的高斯定理虽说是从平板电容器这一特例推 导出，但它却有普适性.
2. 介质中的高斯定理包含了真空中的高斯定理.
真空中: P 0 所以: D 0E P 0E
v D dS
S
S 0E dS qi
vv E dS
S
1
0
qi
3. 电位移矢量D 是一个辅助量.描写电场的基本物理
介质中的高斯定理
大学物理
静电场中的导体和电介质
第4讲 介质中的高斯定理
介质中的高斯定理
§静电场中的电介质有介质时的高斯定理

§静电场中的电介质有介质时的高斯定理

C
S
i
R1 A Q
R2
B
D 4 r q 0 i,
2
r
D 0 , E 0
1 )r R 1
D 4 r2 0
2
i
Q Q 2, E 2 ) R r R 4 r q QD 2 0 i 1 2 D 4 r 4 r i

3 )r R 2
Q Q D 4 r q QD 2, E 0 i 2 4 r 4 r i 0
0 E 0 0
由实验： E
E0



0
r
0 r
' (1 )0 , r
1
εr 1 Q' Q0 εr
五、极化电荷与自由电荷的关系
充满 r 的各向同性均匀电介质的平行板电容器 r 1 0 + + + + + + + + + + + 0, Pσ' r P r E d P ( 1 ) E + + + + + r 0 0 - - - - - - - - - - -

H
+
H

0 104

H

O
CH4 H p 0

-
H2 O
pq r 0
三、电介质的极化
1、无极分子电介质
束缚电荷
无外场时
有外场时 位 移 极 化

p

束 缚 电 荷 ´
三、电介质的极化
2、有极分子电介质 无外场时 有外场时 取 向 极 化

大学物理电磁学部分07电介质的极化和介质中的高斯定理-PPT文档资料

1.介质中的高斯定理
q 0 真空中的高斯定理 E S 0d
S
在介质中，高斯定理改写为：
总场强 自由电荷
0
注意：决定介质极化的不是原来的场 E 0 而是介质内实 际的场 E 。 E '又总是起着减弱总场 E的作用，即起着减弱极化
的作用，故称为退极化场。
10
任一点的总场强为： E E E ' 0
作用下，电介质发生极化；极化强 总结： 在外电场 E 0 度矢量 P 和电介质的形状决定了极化电荷的面密度 ， 而 又激发附加电场 E ， 又影响电介质内部的总电 E 场 E ，而总电场又决定着极化强度矢量 P 。 各物理量的关 E p Pn 0
F
E 0
E0
这种由分子极矩的转向而引起的极化现象称为取向极化
6
外场越大，电矩趋于外场方向一致性越好，电矩 的矢量和也越大。 说明：电子位移极化效应在任何电介质中都存在，而 分子转向极化只是由有极分子构成的电介质所特有的， 只不过在有极分子构成的电介持中，转向极化效应比 位移极化强得多，因而是主要的。
系如下：
E E E ' 0
E'
在电介质中，电位移矢量、极化电荷、附加电场 和总场强这此量是彼此依赖、互相制约的。 为了计算它们当中的任何一个量，都需要和其它量 一起综合加以考虑。 这种连环套的关系太复杂，在实际计算中比较繁 琐。物理学追求“和谐、对称、简洁！
11
四、介质中的高斯定理 电位移矢量
P P cos 极化强度矢量在表面外法线方向上的分量 n
'为电介质表面极化电荷的面密度，
n
n
为极化强度矢量与外法线方向的夹角

07--4、电介质中的电场高斯定理

C U0 C0 U
＋ σ0 － σ’
＋ σ’ － σ 0
+ +
E0
+ -
+ +
+ -
+ E + d
电介质放入电场中，在电介质中
E 0是由自由电荷激发的 E 是由束缚电荷产生的
E E0 E
E0
E
根据电势差与电场间的关系：
U 0 E 0 d , U Ed
或由 E E 0 E 得 E E 0 E 1.02 10 6 2.57 10 5 7.6 10 5 V / m
由此可见，所得的结果相同。
二、有介质时的高斯定理 前面我们已学习了真空中的高斯定理，现在，我们将它推广 到有介质时的情况。我们仍以充满相对介电常数 εr 的平行板电 容器为例进行讨论： + + + + +σ0 极板上的自由电荷面密度为σ0 ， - - σ’ 相邻介质表面的极化电荷面密 度为 -σ’， 根据真空中的高斯定理，在 + + + 电场中任作一闭合曲面 S，通 过该闭合曲面的电通量为： 1 其中q（内）是曲面内所有电 E ds q(内) 荷的代数和。 S
(1) 我们是从平行板电容器这个特例推出有电介质的高斯 定理的，但它是普遍适用的，是静电场的基本规律之一；
D 矢量场，同时计算通过任意曲面的电位移通量，不过要 注意，D 线与 E 线是不同的；
(4) 引入电位移通量后，有介质时的高斯定理可以表述为： “在任意电场中，通过任意一个闭合曲面的电位移通量 等于该面所包围的自由电荷的代数和”。

0

为方便计，我们取如图的长方形闭合曲面 S ，其上、下底面 与极板平行，面积均为 A ，上底面在正极板内，下底面在电介 质内。

《大学物理》有介质的高斯定理


还可用串联求C 还可用串联求
e.g.3:平行板电容器 : 已知: 已知: ε r1 , ε r1 , S,± Q 0 求: , E, P, σ′, C, We 高 D 斯 Solution: 面 D = σ 0 i σ01S/2 + σ01S/2 = Q0 σ 0 i ε = ε 0 ε r1 E= ε = ε0εr 2 E1d = E 2 d ε
第三节 高斯定理
Gauss' Theorem With Dielectric 有介质的
1313-3-1电介质在静电场中 1. 分析 1)真空中的高斯定理 (1)真空中的高斯定理
1 Φ e = ∫∫ E dS = S ε0
+ σ0 σ′
i
+ σ′
E0
σ0
∑q
S in
高 斯 面
(2)有介质时 2)有介质时
D = ε0E + P P
ε r1
S 2 S 2
ε r1 ε r 2
d
Q Sε 0 C= ( ε r1 + ε r 2 ) U ± = E1d = E 2 d C = U± 2d
P = σ' σ'
还可用并联求C 还可用并联求
物理史 (1)
1 r
2+ ε
(History of Physics)
ε << 1 1769 Robinson 万有引力
高 斯 面
σ0
σ0 Q0 ∫∫SE dS = ε0εr s = ε0εr
E'
E
∫∫
S
( ε 0 ε r E ) dS = Q 0
2. 电位移矢量 D (1)分析 1)分析
(2)说明 2)说明 ① D 辅助矢量 M: ③ D, E, P 的关系

2.5 介质中的高斯定理


的介质球带电荷为q 例1：已知半径为a，介电常数为 ε 的介质球带电荷为q， 已知半径为a 球外为空气， 球外为空气，分别在下列情况下求空间各点的电场和介 质中的极化电荷分布： 质中的极化电荷分布： 电荷q均匀分布在球体内； 1）电荷q均匀分布在球体内； 电荷q集中在球心； 2）电荷q集中在球心； 电荷q均匀分布在球面上。 3）电荷q均匀分布在球面上。 解：1）电荷q均匀分布在球体内时，电场分布为 电荷q均匀分布在球体内时，
εK ∇⋅ P = − ρ = ∇⋅ D = ρP = (ε − ε 0 )r 2 ε − ε0 ε −ε0 ε ε
即
由此得到介质球内的自由电荷体密度为
总的自由电荷量
εK q = ∫ ρdV = V ε − ε0
∫
a
0
1 4πεaK 4πr 2 dr = ε − ε0 r2
14
3）介质球内、外的电场强度分别为 介质球内、
P K E1 = = er ε − ε0 ε 0 (ε − ε 0 )r 2 (r < a )
(r > a)
εaK E 2 = er = er 2 4πε 0 r ε 0 (ε − ε 0 )r 2
q
介质球内、 介质球内、外的电位分别为
ϕ1 = ∫ E ⋅ d l = ∫ E1dr + ∫ E2 dr = ∫
1 d 2 K K ρ P = −∇ ⋅ P = − 2 (r ⋅ ) = − 2 r r dr r 的球面上， 在 r = a 的球面上，束缚电荷面密度为 K σ P = n ⋅ P |r =a = e r ⋅ P r =a = a
13
2)由于 2)由于 D = ε 0 E + P ，所以
ε0 ∇ ⋅ D = ε 0∇ ⋅ E + ∇ ⋅ P = ∇ ⋅ D + ∇ ⋅ P ε ε0 (1 − )∇ ⋅ D = ∇ ⋅ P ε

介质中高斯定理的微分形式

介质中高斯定理的微分形式高斯定理是电磁学中的一个基本定理，它是通过研究电场的通量来描述电场的性质。

具体来说，高斯定理是由德国数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）在19世纪初提出的。

在电磁学中，高斯定理有两种形式：积分形式和微分形式。

这里我们将重点论述高斯定理的微分形式。

高斯定理的微分形式是通过研究电场的散度来描述电场分布情况的。

它的数学表达形式为：∇·E=ρ/ε₀（1）式中，∇·E表示电场E的散度；ρ表示电荷密度；ε₀表示真空中的电介质常数。

需要注意的是，由于微分形式仅仅描述了一个点的电场分布情况，因此我们通常将高斯定理的微分形式用于研究电场的局部性质。

要理解高斯定理的微分形式，我们首先需要了解电场的散度概念。

电场的散度表示电场在一个给定点上的流出和流入情况。

如果一个点的电场流出大于流入，那么电场的散度为正；如果一个点的电场流入大于流出，那么电场的散度为负；如果一个点的电场流入和流出相等，那么电场的散度为零。

因此，散度代表了电场的源和汇情况。

根据高斯定理的微分形式，我们可以得到以下几个重要结论：1.电场的散度与电荷密度的关系：根据式(1)，我们可以看出，电场的散度正比于电荷密度。

如果一个区域内部存在着电荷密度，那么该区域内的电场就具有正的散度；如果一个区域内的电荷密度为零，那么该区域内的电场散度也为零。

这意味着电场的散度能够描述电场源的分布情况。

2.空间中的电场流量：根据高斯散度定理，对于一个封闭曲面S，通过该曲面的电场流量等于该曲面内的电荷总量。

具体数学表达为：∮SE·dS=∫∫∫V(∇·E)dV=(∫∫∫Vρ/ε₀)dV（2）式中，∮S表示对封闭曲面S的面积分；∫∫∫V表示对整个空间V的体积分；ρ表示电荷密度；ε₀表示真空中的电介质常数。

由式(2)可知，封闭曲面S内的电场流量正比于该曲面内的电荷总量。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

10
总度结矢：量在P和外电电介场质E的0作形用状下决，定电了介极质化发电生荷极的化面；密极度化强，
而场各物E理又，量激而的发总关附电加场E电0又场决E定，着pE极又化影强响度电矢介量质内P部。Pn的总电
系如下：
EE0E' E'
在电介质中，电位移矢量、极化电荷、附加电场 和总场强这此量是彼此依赖、互相制约的。
计规律。
在外电场中，在有极分子电介
质表面出现极化电荷，
E 0 F
E0
这种由分子极矩的转向而引起的极化现象称为取向极化
6
外场越大，电矩趋于外场方向一致性越好，电矩 的矢量和也越大。
说明：电子位移极化效应在任何电介质中都存在，而 分子转向极化只是由有极分子构成的电介质所特有的， 只不过在有极分子构成的电介持中，转向极化效应比 位移极化强得多，因而是主要的。
代替电介质对电 场的影响。
在外电场
E
中，介质极化产生的束
0
缚部电都荷产， 生在 附其 加周 电围 场无E论'，介称质为内退部极还化是场外。
' '
退极化场
任一点的总场强为： EE0E'
注意：决定介质极化的不是原来的场
际的 场 E。
E
而是介质内实
0
E'又总是起着减弱总场 E的作用，即起着减弱极化
的作用，故称为退极化场。
为了计算它们当中的任何一个量，都需要和其它量 一起综合加以考虑。
这种连环套的关系太复杂，在实际计算中比较繁 琐。物理学追求“和谐、对称、简洁！
11
四、介质中的高斯定理 电位移矢量
1.介质中的高斯定理
真空中的高斯定理 SE0dS
q0
0
在介质中，高斯定理改写为：
总场强
自由电荷
1
EdS
S
0
S
(q0q')
束缚电荷
PdS q'
SE S(d0 S E P 1 0)SdS q 0 S10q0 SP dS •定义：DS电de位f移0E矢量PS
12
S(0EP )dS q0
• 定义：电d位ef移矢量
S
自由电荷
D0EP
SDdSq0
介质中的高斯定理
S
建立电位移线：
1）线上每一点的切线方向为该点电位移矢量的方向；
所产生的电荷称之为“极化电荷”。
E0
在电介质上出现的极化电荷是正负
电荷在分子范围内微小移动的结果，
所以极化电荷也叫“束缚电荷”。
2
电介质内部的总场强 EE0E' E0
极化电荷所产生的附加电场不足
以将介质中的外电场完全抵消，它只
E'
E0
E
能削弱外电场。 介质内部的总场强不为零！
在各向同性均匀电介质中：
2）通过垂直于电位移矢量的单位面积的电位移线数
目应等于该点电位移矢量的大小。
DSDdS
称为穿过闭合面S的电位移通量。
介质中的高斯定理：
DdS
S
q0
S
介质中的高斯定理意义：通过任一闭合曲面的电位移
1）不管是位移极化还是取向极化，其最后的宏观 效果都是产生了极化电荷。
综 2）两种极化都是外场越强，极化越厉害，所产生 述：的分子电矩的矢量和也越大。
3）极化电荷被束缚在介质表面，不能离开电介质 到其它带电体，也不能在电介质内部自由移动。它 不象导体中的自由电荷能用传导方法将其引走。
7
二、极化强度矢量
为极化强度 矢量与外法线方向的夹角 通常定义en为介质外法线方向。
下关在系电：介质的P内d部S，极化强q度' 与极化电荷之间有如 S Si n s i d e
在任一闭合曲面内极化电荷的负值等于极化强度的通量。
9
三、退极化场
+Q
–Q
电介质在外场中的性质相当于在
真空中有适当的束缚电荷体密度分布
在其内部。因此可用 ' 和 '的分布来
描述介质在电场中各点的极化状态（极化程度和方 向）的物理量。 在宏观上测量到的是大量分子电偶极矩的统计平均值，
（1）定义：介质中某一点的电极化强度矢量等于这一
点电处极单化位强体度积矢的量分：子P 电 偶极P矩ei 的矢单量位和：。[库仑/米2]
V
其中 pei是第i个分子的电偶极矩；
注意: 介质极化也 有均匀极化与非均
静电场中的电介质 介质中的高斯定理
(第五章第1~3节 )
1
从电场这一角度看，电介质就是绝缘体。 特点：电介质体内只有极少自由电子。
我们只讨论静电场与各向同性电介质的相互作用。
一、静电场对电介质的作用—荷。
这种在外电场作用下电介质表面
出现电荷的现象叫做电介质的极化。
E
E0
2.电介质极化的微观机制
r
r 称为相对
介电常数或
电容率。
从电学性质看电介质的分子可分为两类：无极分子、
有极分子。
每个分子负电荷对外影响均可等效为 单独一个静止的负电荷 的作用。其大小为 分子中所有负电之和，这个等效负电荷的 作用位置称为分子的“负电作用中心”。
-
3
同样，所有正电荷的作用也可等效一
位移极化主要是由电子的移动造成的。
5
（2）有极分子电介质的极化
•在没有外电场时，有极分子正负电
荷中心不重合，分子存在固有电偶
极矩。但介质中的电偶极子排列杂
乱,宏观不显极性。
•有外场时电偶极子在外场作用下
发生转向，使电偶极矩方向趋近于
与外场一致所致。
F
由于分子的无规则热运动，
这种转向只能是部分的，遵守统
++
+
H2O
+
4
（1）无极分子电介质的极化
•在没有外电场时，无极分子没有电偶极矩，分子不
显电性。
•有外场时呈现极性。
位移极化
这种由于正电中心和负 电中心的移动而形成的极 化现象叫做位移极化。
P
E0
均匀介质极化时在介质表面出
E0
现极化电荷，
非均匀介质极化时，介质的表
面及内部均可出现极化电荷。
外场越强，分子电矩的矢量和越大，极化也越厉害。
V宏观无限小微观无限大；
匀极化之分。
说明： 1.真空中 P = 0 ，真空中无电介质。 2.导体内 P = 0 ，导体内不存在电偶极子。
8
（2）极化（束缚）电荷与极化强度的关系
如下在关电系介：质的'表Pn面上P，c极o化s强P度与en极化电荷之间有 '为电介质表面极化电荷的面密度，
Pn Pcos极化强度矢量在表面外法线方向上的分量
个静止的正电荷的作用，这个等效正电 荷作用的位置称为“正电作用中心”。
+
无极分子：正负电荷作用中心重合的分子；
如H2、N2、O2、CO2
在无外场作用下整个分子无电矩。
+
+-
有极分子：正负电荷作用中心不重
合的分子。
H2
- 如H2O、CO、SO2、NH3…..
O
有极分子对外影响等效为一 H+
H+
-
个电偶极子，在无外场作用下存 在固有电偶极矩。