三角高程测量的计算实例

三角高程测量题目
题目：
已知A、B两点高差为HA = 36.72m，视差距离为DB = 36.50m，实际距离AB = 200m，试求A、B两点间的水平距离（用全站仪测量法）
回答：
三角高程测量是通过测量两个控制点之间的高差来求两点间水平距离的方法。

根据题意，已知A、B两点高差HA = 36.72m，视差距离DB = 36.50m，实际距离AB = 200m。

首先，我们需要确定全站仪的安置位置，通常选择在控制点C上。

然后，通过全站仪的视准线和三角高程测量方法，可以求得A、B两点间的水平距离。

具体步骤如下：
1. 将全站仪安置在控制点C上，对中、整平。

2. 将仪器望远镜对准A点棱镜中心，调整望远镜的垂直和水平微调，使十字丝对准棱镜中心。

3. 打开全站仪的测距按钮，测出A、B两点间的高差HAB。

4. 根据已知的HA和AB，可求得两点间的水平距离DAB。

根据三角高程测量的原理，有：HAB = HA + DB + DAB
其中，DAB即为A、B两点间的水平距离。

代入已知数据可得：DAB = AB - DB - HA = 200 - 36.5 - 36.72 = 126.88m
因此，A、B两点间的水平距离为126.88m。

总结：
通过三角高程测量方法，我们能够求得两个控制点之间的高差和水平距离。

在实际应用中，需要注意仪器的安置、对中、整平和读数误差等问题，以确保测量结果的准确性和可靠性。

同时，对于不同的情况和环境，可能需要采用不同的测量方法和仪器，因此需要灵活运用相关知识，结合实际情况进行选择和应用。

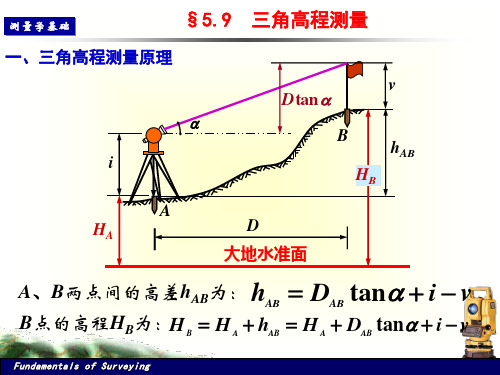
2.4三角高程2.4.1三角高程测量原理1、原理三角高程测量的基本思想是根据由测站向照准点所观测的垂直角（或天顶距）和它们之间的水平距离，计算测站点与照准点之间的高差。

这种方法简便灵活，受地形条件的限制较少，故适用于测定三角点的高程。

三角点的高程主要是作为各种比例尺测图的高程控制的一部分。

一般都是在一定密度的水准网控制下，用三角高程测量的方法测定三角点的高程。

如下图：现在计划测量A、B间高差,在A点架设仪器，B点立标尺。

量取仪器高，使望远镜瞄准B上一点M,它距B点的高度为目标高，测出水平和倾斜视线的夹角α，若A、B水平距离S已知，则：注意：上式中α可根据仰角或俯角有正负值之分，当取仪器高=目标高时，计算就方便了。

在已知点架站测的高差叫直占、反之为反战。

2、地球曲率与大气对测量的影响我们在水准测量中知道，高程的测量受地球曲率的影响，仪器架在中间可以消除，三角高程也能这样，但是对于一些独立交会点就不行了。

三角高程还受大气折射的影响。

如图：加设A点的高程为,在A点架设仪器测量求出B点的高程。

如图可以得出但如图有两个影响：1）、地球曲率，在前面我们已经知道，地球曲率改正2）、大气折射不易确定，一般测量中把折射曲线近似看作圆弧，其平均半径为地球半径的6~7倍，则：，在这里r就是图上的f2。

通常，我们令下面求，如图，在三角形中:，当测量范围在20km以内，可以用S代替L，然后对公式做一适当的改正，进行计算。

2.4.2竖盘的构造及竖角的测定1、竖盘构造1）、构造有竖盘指标水准管，如图：竖盘与望远镜连在一起，转动望远镜是竖盘一起跟着转动；但是竖盘指标和指标水准管在一起，他们不动，只有调节竖盘水准管微动螺旋式才会移动。

通常让指标水准管气泡居中时进行读数。

竖盘自动归零装置2）、竖盘的注记形式主要有顺时针和逆时针望远镜水平，读数为90度的倍数角度。

3）、竖角的表示形式高度角a：目标视线与水平方向的夹角天顶距z：目标视线与天顶距方向的夹角2、竖角及测定定义：竖直面内目标方向与水平方向的夹角。

三角高程测量原理及应用 Revised by Hanlin on 10 January 2021三角高程测量及其误差分析与应用一、三角高程测量的基本原理三角高程测量是通过观测两点间的水平距离和天顶距（或高度角）求定两点间的高差的方法。

它观测方法简单，不受地形条件限制，是测定大地控制点高程的基本方法。

如图1,所示，在地面上A,B两点间测定高差hAB,A点设置仪器，在B点竖立标尺。

量取望远镜旋转轴中心I至地面点上A点的仪器高i1，用望远镜中的十字丝的横丝照准B点标尺上的一点M，它距B点的高度称为目标高i2，测出倾斜视线与水平线所夹的竖角为a，若A,B两点间的水平距离已知为S，则由图可得图1如图1,所示，在地面上A,B两点间测定高差hAB,A点设置仪器，在B点竖立标尺。

量取望远镜旋转轴中心至地面点上A点的仪器高i，用望远镜中的十字丝的横丝照准B点标尺，它距B点的高度称为目标高v，测出倾斜视线与水平线所夹的竖角为a，若A,B两点间的水平距离已知为s，则由图可得，AB两点间高差的公式为：若A点的高程已知为HA,则B点的高程为：但是，在实际的三角高程测量中，地球曲率、大气折光等因素对测量结果精度的影响非常大，必须纳入考虑分析的范围。

因而，出现了各种不同的三角高程测量方法，主要分为：单向观测法，对向观测法，以及中间观测法。

1.1单向观测法单向观测法是最基本最简单的三角高程测量方法，它直接在已知点对待测点进行观测，然后在①式的基础上加上大气折光和地球曲率的改正，就得到待测点的高程。

这种方法操作简单，但是大气折光和地球曲率的改正不便计算，因而精度相对较低。

1.2对向观测法对向观测法是目前使用比较多的一种方法。

对向观测法同样要在A点设站进行观测，不同的是在此同时，还在B点设站，在A架设棱镜进行对向观测。

从而就可以得到两个观测量：直觇：h AB =S往tanα往+i往-v往+c往+r往②反觇：h BA =S返tanα返+i返-v返+c返+r返③S——A、B间的水平距离；α——观测时的高度角；i——仪器高；v——棱镜高；c——地球曲率改正；r——大气折光改正。

中点单觇法三角高程测量的误差及精度分析摘要：本文主要探讨了中点单觇法三角高程测量中可能出现的误差及其精度分析。

首先，介绍了中点单觇法三角高程测量的基本原理和方法，然后分析了误差来源及其影响因素，最后对精度进行了分析，并给出了精度计算公式和实例。

关键词：中点单觇法；三角高程测量；误差分析；精度分析正文：一、中点单觇法三角高程测量基本原理和方法中点单觇法是三角高程测量中常用的一种方法。

其基本原理是在一定水平距离上设置两个观测点（称为A点和B点），并以两个观测点及目标物（称为C点）形成的三角形为基础，通过测量三角形三个内角，计算出目标物的高程。

中点单觇法的测量方法如下：1. 在距离目标物一定距离的A、B两点上分别设置测距仪。

2. A、B两个测距仪同时测量目标物到各自测距仪的距离。

3. A、B两个测距仪同时记录目标物与A、B两点的连线在水平方向上的夹角。

4. 利用三角函数和测量数据计算出目标物的高程。

二、误差来源及其影响因素中点单觇法三角高程测量中可能存在的误差主要包括观测误差、仪器误差、环境误差和计算误差等。

其中观测误差是指由于人为或自然因素造成的误差；仪器误差是指由于仪器本身的精度、灵敏度等因素引起的误差；环境误差是指由于气象、地形、天气等环境因素引起的误差；计算误差是指由于计算方法和步骤引起的误差。

影响中点单觇法三角高程测量精度的因素主要包括：1. 测量设备的精度和灵敏度2. 测量人员的水平和经验3. 环境因素的影响4. 测量方法选择的科学性和合理性三、精度分析及计算公式为了提高中点单觇法三角高程测量的精度，需要针对误差来源和影响因素进行分析，并采取相应的措施加以消减。

一般情况下，中点单觇法的精度可以通过以下公式进行计算：（式中，K为系数，a为目标物与A点的距离，b为目标物与B点的距离，α、β、γ分别为A、B、C三角形三个内角）具体的精度计算实例如下：假设A、B两点距离为100米，目标物离A、B两点的距离分别为70米和50米，并且测量误差为±1毫米，则根据上述公式计算得到中点单觇法的测量精度为：K=0.00179α=54.44°β=35.56°γ=90.00°a=70mb=50m∆H=2.0303×10^-4m四、结论中点单觇法三角高程测量是一种简单、直观、可靠的高程测量方法，但其精度受到多种因素的影响。

J08-KC-08-A三角高程测量1 三角高程测量基本公式仪器高 1i觇标高 2v 参考椭球面 A ′B ′ 水准面 PE ，AF切线PC （水准面PE 的） 切线PM （也就是视线）光程曲线PN （切线PM 的光程曲线） 垂直角12α，实测的，但真正的垂直角应为0α，012αα-称为折光角图1 三角高程测量示意图高差计算公式为：NB MN EF CE MC BF h --++==12 （1）220120120221v s RK i s R tg s --++=α 2120120v i Cs tg s -++=α式中：C ——球气差系数，C =（1-K ）/2R0s ——为实测的水平距离221s R ——地球弯曲差22s R K ——大气垂直折光差，K 为折光系数，一般在0.1～0.16之间，可用实验方法测定。

2 三角高程导线测量基本要求（1） 三、四等及等外高程导线测量，每公里高差中数的偶然中误差∆M 和全中误差wM 应符合表1的规定。

表 1 mm（2） 高程导线天顶距测量，一测回观测值中误差Z M 应符合以下规定。

三等 "3.1≤Z M 四等 "5.1≤Z M（3） 各等级高程导线的路线长度应符合表2的规定。

表 2 km（4） 高程导线的环线、附合路线闭合差和检查已测测段高差之差，不得超过表3的规定。

表 3 mm（5） 高程导线的视线长度和视线倾角应符合表4的规定。

J08-KC-08-A4 m表表5 m表 6 （°）3 三角高程导线测量流程3.1 路线设计与埋石（1）高程导线的路线设计应根据任务书的要求，收集测区及附近的地形图、交通图、水准点、气象等方面的资料，设计最佳方案，编写技术设计。

（2）测站和置觇点宜选择在高出周围地面的地形特征点上，尽量提高视线的高度。

视线高度和地面障碍物的距离不小于1.5m。

（3）视线和置觇点应尽量避免通过有强烈背景光和强磁场的地方，以及有吸热、散热变化大的区域，视线离较宽的水面和高压输电线的距离应大于2m。

三角高程测量是一种常用的测量方法，它可以用来测量地面上点的准确高程。

在这篇文章中，我们将着重介绍三角高程测量中的往返观测计算公式。

一、三角高程测量原理三角高程测量是利用三角形的相似性原理，通过已知两点的高程和这两点到待测点的水平距离，来计算待测点的高程。

三角高程测量的基本原理如下：1. 在地面上选择一个已知高程的点A，以及要测量高程的点P。

2. 通过测量仪器测量点A和点P之间的水平距离d和两点的高程差h。

3. 通过三角函数计算出点P的高程。

二、三角高程测量的往返观测在实际测量中，为了提高精度，常常采用往返观测的方法进行测量。

往返观测的原理是利用观测仪器来回测量两点之间的距离和高程差，然后取平均值作为最终结果，以减小由于观测仪器误差、大气温度、大气压力等因素造成的误差。

三、三角高程测量往返观测计算公式往返观测的三角高程测量计算公式如下：1. 求点P的高程差首先需要计算出点P的高程差，使用以下公式：\[ \Delta h = h_1 - h_2 \]其中，\(h_1\) 为第一次测量的高程，\(h_2\) 为第二次测量的高程。

2. 求两次测量的平均距离将两次测量的距离\(d_1\)和\(d_2\)求均值，得到平均距离：\[ \bar{d} = \frac{d_1 + d_2}{2} \]3. 计算点P的高程利用三角函数计算出点P的高程：\[ H = h_2 + \frac{\Delta h \times \bar{d}}{d_2} \]其中，\(H\)为最终计算出的点P的高程。

四、注意事项在进行三角高程测量的往返观测时，需要注意以下几点：1. 观测仪器的选择和校准非常重要，需要保证其精度和稳定性。

2. 大气温度和大气压力对测量结果有较大影响，需要进行相应的修正。

3. 观测时需要注意周围环境的影响，避免受到建筑物、树木、地形等因素干扰。

4. 测量终点的选取应当避免大坡度地形，以减小误差。

通过以上介绍，我们了解了三角高程测量中的往返观测计算公式及其应用注意事项。