春季五年制小学奥数四年级奇数与偶数(上)

个人收集整理-ZQ例：······，结果是偶数还是奇数？分析与解答：方法一：利用求和公式直接求和，可判断和地奇偶性等差数列地和（首项末项）×项数÷······（）×÷（）×因为是偶数，偶数与任一自然数地积仍是偶数，所以和是偶数方法二：在自然数列中，奇数与偶数相同排列，在这个自然数中，奇数、偶数各有（个），个奇数或偶数地和都是偶数.两个偶数地和是偶数，所以······地和是偶数.个人收集整理勿做商业用途练习：、任意取出个连续自然数，它们地总和是奇数还是偶数？、用，，，······十个数字组成五个两位数，每个数字只用一次，要求它们地和是一个奇数，并且尽可能大，那么这五个两位数地和是多少？个人收集整理勿做商业用途、判断××××地积是偶数还是奇数？、已知，请判断是奇数还是偶数？例．有张扑克牌，画面向上.小明每次翻转其中地张，那么，他能在翻动若干次后，使张牌地画面都向下吗？个人收集整理勿做商业用途分析与解答：同学们可以试验一下，只有将一张牌翻动奇数次，才能使它地画面由向上变为向下.要想使张牌地画面都向下，那么每张牌都要翻动奇数次.个人收集整理勿做商业用途个奇数地和是奇数，所以翻动地总张数为奇数时才能使张牌地牌面都向下.而小明每次翻动张，不管翻多少次，翻动地总张数都是偶数.个人收集整理勿做商业用途所以无论他翻动多少次，都不能使张牌画面都向下.练习：、小明涮了个碗，碗口向上地摆在桌上，他想每次翻转个碗，使它们地碗口转向相反地方向.翻转到某一时候，他能不能使碗口都向下呢？如果是个碗，每次翻转个呢？个人收集整理勿做商业用途、有张扑克牌，画面朝上，小刚每次翻转其中地张.他能在翻转若干次后，使张牌地画面都向下吗？、个小朋友排成一排（站地方向相同），做“向后转”地游戏，每次其中地个小朋友做向后转地动作，能否经过若干次后使个小朋友全部改变站地方向？请说明理由.个人收集整理勿做商业用途、电影院里有盏电灯，每盏灯由一根灯绳控制，拉一下亮.个学生依次进入电影院，第一个学生把地倍数地灯绳拉一下，灯全亮了，第二个学生把地倍数地灯绳都拉一下，第三个学生把地倍数地拉一下，······第个学生把地倍数地拉一下，最后，礼堂里有哪些灯是亮地？个人收集整理勿做商业用途1 / 1。

3本讲知识点属于数论大板块内的“定性分析”部分，小学生的数学思维模式大多为“纯粹的定量计算”，拿到一个题就先去试数，或者是找规律，在性质分析层面几乎为0，本讲力求实现的一个主要目标是提高孩子对数学的严密分析能力，培养孩子明白做题前有时要“先看能不能这么做，再去动手做”的思维模式。

无论是小升初还是杯赛会经常遇到，但不会单独出题，而是结合其他知识点来考察学生综合能力。

一、奇数和偶数的定义 整数可以分成奇数和偶数两大类.能被2整除的数叫做偶数，不能被2整除的数叫做奇数。

通常偶数可以用2k （k 为整数）表示，奇数则可以用2k +1（k 为整数）表示。

特别注意，因为0能被2整除，所以0是偶数。

二、奇数与偶数的运算性质性质1：偶数±偶数=偶数，奇数±奇数=偶数性质2：偶数±奇数=奇数性质3：偶数个奇数的和或差是偶数性质4：奇数个奇数的和或差是奇数性质5：偶数×奇数=偶数，奇数×奇数=奇数，偶数×偶数=偶数三、两个实用的推论推论1：在加减法中偶数不改变运算结果奇偶性，奇数改变运算结果的奇偶性。

推论2：对于任意2个整数a,b ,有a+b 与a-b 同奇或同偶模块一、奇数偶数基本概念及基本加减法运算性质【例 1】 1231993++++……的和是奇数还是偶数？【巩固】 2930318788+++++……得数是奇数还是偶数？【巩固】 (200201202288151152153233++++-++++……）（……）得数是奇数还是偶数？例题精讲 知识点拨教学目标5-1奇数与偶数【巩固】123456799100999897967654321+++++++++++++++++++++的和是奇数还是偶数？为什么？【巩固】东东在做算术题时，写出了如下一个等式：1038137564=⨯+，他做得对吗？【例 3】能否在下式的“□”内填入加号或减号，使等式成立，若能请填入符号，不能请说明理由⑴1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9＝10⑵1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9＝27【例 4】能否从四个3，三个5，两个7中选出5个数，使这5个数的和等于22.【巩固】能否从四个6，三个10，两个14中选出5个数，使这5个数的和等于44.【例 5】一个自然数数分别与另外两个相邻奇数相乘，所得的两个积相差150，那么这个数是多少？【巩固】一个偶数分别与其相邻的两个偶数相乘，所得的两个乘积相差80，那么这三个偶数的和是多少？【例 6】多米诺骨牌是由塑料制成的1×2长方形，共28张，每张牌上的两个1×1正方形中刻有“点”，点的个数分别为0，1，2，…，6个不等，其中7张牌两端的点数一样，即两个0，两个1，…，两个6；其余21张牌两端的点数不一样，所谓连牌规则是指：每相邻两张牌必须有一端的点数相同，且以点数相同的端相连，例如：…………现将一付多米诺骨牌按连牌规则连成一条链，如果在链的一端为6点，那么在链的另一端为多少点?并简述你的理由．【巩固】一条线段上分布着n个点，这些点的颜色不是黑的就是白的，它们将线段分为n+1段，已知线段两端的两个点都是黑的，而中间的每一个点的两边各有一黑一白.那么白点的数目是奇数还是偶数？模块二、奇偶运算性质综合及代数分析法【巩固】是否存在自然数a、b、c，使得(a-b)(b-c)(a-c)=45327？【巩固】a、b、c三个数的和与它们的积的和为奇数，问这三个数中最多可以有几个奇数？【例 8】已知a,b,c中有一个是511，一个是622，一个是793。

一、奇数与偶数一、新学：1.奇数和偶数整数可以分成奇数和偶数两大 .能被 2 整除的数叫做偶数，不能被 2 整除的数叫做奇数。

偶数通常可以用 2k（k 整数）表示，奇数可以用 2k+1（k 整数）表示。

特注意，因 0 能被 2 整除，所以 0 是偶数。

2.奇数与偶数的运算性性 1：偶数±偶数 =偶数，奇数±奇数 =偶数。

性 2：偶数±奇数 =奇数。

性 3：偶数个奇数相加得偶数。

性 4：奇数个奇数相加得奇数。

性 5：偶数×奇数 =偶数，奇数×奇数 =奇数。

利用奇数与偶数的些性，我可以精巧地解决多.二、例例 11+2+3+⋯+1993的和是奇数？是偶数？例 2 一个数分与另外两个相奇数相乘，所得的两个相差150，个数是多少？例 3 元旦前夕，同学相互送年卡 .每人只要接到方年卡就一定回年卡，那么送了奇数年卡的人数是奇数，是偶数？什么？例 4 已知 a、b、c 中有一个是 5，一个是 6，一个是 7.求 a-1，b-2，c-3的乘一定是偶数。

例 5 任意改某一个三位数的各位数字的序得到一个新数 .新数与原数之和不能等于 999。

例 7桌上有 9 只杯子，全部口朝上，每次将其中 6只同时“翻转”请.说明：无论经过多少次这样的“翻转”，都不能使 9 只杯子全部口朝下。

例 8假设 n 盏有拉线开关的灯亮着，规定每次拉动（n-1）个开关，能否把所有的灯都关上？请证明此结论，或给出一种关灯的办法。

例 9 在圆周上有 1987 个珠子，给每一珠子染两次颜色，或两次全红，或两次全蓝，或一次红、一次蓝 .最后统计有 1987 次染红， 1987 次染蓝 .求证至少有一珠子被染上过红、蓝两种颜色。

例 10 某校六年级学生参加区数学竞赛，试题共 40 道，评分标准是：答对一题给 3 分，答错一题倒扣 1 分.某题不答给 1 分，请说明该校六年级参赛学生得分总和一定是偶数。

奇数与偶数例1：1+2+3+······+2008，结果是偶数还是奇数？分析与解答：方法一：利用求和公式直接求和，可判断和的奇偶性等差数列的和=（首项+末项）×项数÷21+2+3+······+2008=（1+2008）×2008÷2=（1+2008）×1004因为1004是偶数，偶数与任一自然数的积仍是偶数，所以和是偶数方法二：在自然数列中，奇数与偶数相同排列，在1-2008这2008个自然数中，奇数、偶数各有2008/2=1004（个），1004个奇数或偶数的和都是偶数。

两个偶数的和是偶数，所以1+2+3+······+2008的和是偶数。

练习：1、任意取出1994个连续自然数，它们的总和是奇数还是偶数？2、用0，1，2，3······9十个数字组成五个两位数，每个数字只用一次，要求它们的和是一个奇数，并且尽可能大，那么这五个两位数的和是多少？3、判断23×47×65×132×239的积是偶数还是奇数？4、已知83+95+77+89+A=2001，请判断A是奇数还是偶数？例2．有5张扑克牌，画面向上。

小明每次翻转其中的4张，那么，他能在翻动若干次后，使5张牌的画面都向下吗？分析与解答：同学们可以试验一下，只有将一张牌翻动奇数次，才能使它的画面由向上变为向下。

要想使5张牌的画面都向下，那么每张牌都要翻动奇数次。

5个奇数的和是奇数，所以翻动的总张数为奇数时才能使5张牌的牌面都向下。

而小明每次翻动4张，不管翻多少次，翻动的总张数都是偶数。

所以无论他翻动多少次，都不能使5张牌画面都向下。

5-1奇數與偶數的性質與應用教學目標本講知識點屬於數論大板塊內的“定性分析”部分，小學生的數學思維模式大多為“純粹的定量計算，拿到一個題就先去試數，或者是找規律，在性質分析層面幾乎為0，本講力求實現的一個主要目標是提高孩子對數學的嚴密分析能力，培養孩子明白做題前有時要“先看能不能這麼做，再去動手做”的思維模式。

無論是小升初還是杯賽會經常遇到，但不會單獨出題，而是結合其他知識點來考察學生綜合能力。

知識點撥一、奇數和偶數的定義整數可以分成奇數和偶數兩大類.能被2整除的數叫做偶數，不能被2整除的數叫做奇數。

通常偶數可以用2k（k為整數）表示，奇數則可以用2k+1（k 為整數）表示。

特別注意，因為0能被2整除，所以0是偶數。

二、奇數與偶數的運算性質性質1：偶數±偶數=偶數，奇數±奇數=偶數性質2：偶數±奇數=奇數性質3：偶數個奇數的和或差是偶數性質4：奇數個奇數的和或差是奇數性質5：偶數×奇數=偶數，奇數×奇數=奇數，偶數×偶數=偶數三、兩個實用的推論推論1：在加減法中偶數不改變運算結果奇偶性，奇數改變運算結果的奇偶性。

推論2：對於任意2個整數a,b ,有a+b與a-b同奇或同偶例題精講模組一、奇偶分析法之計算法【例 1】1231993++++……的和是奇數還是偶數？【考點】奇偶分析法之計算法【難度】2星【題型】解答【解析】在1至1993中，共有1993個連續自然數，其中997個奇數，996個偶數，即共有奇數個奇數，那麼原式的計算結果為奇數.【答案】奇數【例 1】從1開始的前2005個整數的和是______數(填：“奇”或“偶”)。

【考點】奇偶分析法之計算法【難度】2星【題型】填空【關鍵字】希望杯，4年級，初賽，5題【解析】1+2+3+…+2004+2005=(1+2005)×2005÷2=1003×2005是奇數【答案】奇數【巩固】2930318788+++++……得數是奇數還是偶數？【考點】奇偶分析法之計算法【難度】2星【題型】解答【解析】偶數。

第二讲：奇数与偶数教学目标本讲知识点属于数论大板块内的“定性分析”部分，小学生的数学思维模式大多为“纯粹的定量计算，拿到一个题就先去试数，或者是找规律，在性质分析层面几乎为0，本讲力求实现的一个主要目标是提高孩子对数学的严密分析能力，培养孩子明白做题前有时要“先看能不能这么做，再去动手做”的思维模式。

无论是小升初还是杯赛会经常遇到，但不会单独出题，而是结合其他知识点来考察学生综合能力。

知识点拨一、奇数和偶数的定义整数可以分成奇数和偶数两大类.能被2整除的数叫做偶数，不能被2整除的数叫做奇数。

通常偶数可以用2k（k为整数）表示，奇数则可以用2k+1（k为整数）表示。

特别注意，因为0能被2整除，所以0是偶数。

二、奇数与偶数的运算性质性质1：偶数±偶数=偶数，奇数±奇数=偶数性质2：偶数±奇数=奇数性质3：偶数个奇数的和或差是偶数性质4：奇数个奇数的和或差是奇数性质5：偶数×奇数=偶数，奇数×奇数=奇数，偶数×偶数=偶数三、两个实用的推论：推论1：在加减法中偶数不改变运算结果奇偶性，奇数改变运算结果的奇偶性。

推论2：对于任意2个整数a,b ,有a+b 与a-b 同奇或同偶模块一：奇数偶数基本概念及基本加减法运算性质【例 1】 1231993++++……的和是奇数还是偶数？【解析】 在1至1993中，共有1993个连续自然数，其中997个奇数，996个偶数，即共有奇数个奇数，那么原式的计算结果为奇数【巩固】 123456799100999897967654321+++++++++++++++++++++L L 的和是奇数还是偶数？为什么？【解析】 在算式中，1~99都出现了2次，所以123499999897964321++++++++++++++L L 是偶数，而100也是偶数，所以1234567991009998979676++++++++++++++++L L54321+++++的和是偶数．【巩固】 2930318788+++++……得数是奇数还是偶数？【解析】 偶数。

学生课程讲义
我们把学过的整数按从小到大的顺序写出来,可以写成：
0,1,2,3,4……
在学习和生活中,我们经常把上述这些数分成两大类,其中一类叫做偶数, 它们是：
0,2,4,6,8,10,……
另一类叫做奇数, 他们是：
1,3,5,7，9,……
如果一个整数可以被2整除,那么我们说这个数是偶数.如果一个整数不是偶数,那么它一定是奇数。

一个整数是偶数还是奇数,是这个整数自身的一种性质.这种性质,叫做奇
偶性
在这一讲中,我们向大家介绍奇数和偶数的三个最常见的性质
性质1任何一个奇数一定不等于任何一个偶数.(例如3≠4)
性质2相邻的两个自然数总是一奇
性质3有趣的运算规律
奇数士奇数=偶数
偶数士偶数=偶数
奇数士偶数=奇数
偶数士奇数=奇数
奇数×奇数=奇数
奇数×偶数=偶数
偶数×偶数=偶数
奇数不可能被偶数整除。

一、奇数与偶数一、新课学习：1.奇数和偶数整数可以分成奇数和偶数两大类.能被2整除的数叫做偶数，不能被2整除的数叫做奇数。

偶数通常可以用2k（k为整数）表示，奇数则可以用2k+1（k为整数）表示。

特别注意，因为0能被2整除，所以0是偶数。

2.奇数与偶数的运算性质性质1：偶数±偶数=偶数，奇数±奇数=偶数。

性质2：偶数±奇数=奇数。

性质3：偶数个奇数相加得偶数。

性质4：奇数个奇数相加得奇数。

性质5：偶数×奇数=偶数，奇数×奇数=奇数。

利用奇数与偶数的这些性质，我们可以精巧地解决许多实际问题.二、例题例11+2+3+…+1993的和是奇数？还是偶数？例2一个数分别与另外两个相邻奇数相乘，所得的两个积相差150，这个数是多少？例3元旦前夕，同学们相互送贺年卡.每人只要接到对方贺年卡就一定回赠贺年卡，那么送了奇数张贺年卡的人数是奇数，还是偶数？为什么？例4已知a、b、c中有一个是5，一个是6，一个是7.求证a-1，b-2，c-3的乘积一定是偶数。

例5任意改变某一个三位数的各位数字的顺序得到一个新数.试证新数与原数之和不能等于999。

例7桌上有9只杯子，全部口朝上，每次将其中6只同时“翻转”.请说明：无论经过多少次这样的“翻转”，都不能使9只杯子全部口朝下。

例8假设n盏有拉线开关的灯亮着，规定每次拉动（n-1）个开关，能否把所有的灯都关上？请证明此结论，或给出一种关灯的办法。

例9在圆周上有1987个珠子，给每一珠子染两次颜色，或两次全红，或两次全蓝，或一次红、一次蓝.最后统计有1987次染红，1987次染蓝.求证至少有一珠子被染上过红、蓝两种颜色。

例10某校六年级学生参加区数学竞赛，试题共40道，评分标准是：答对一题给3分，答错一题倒扣1分.某题不答给1分，请说明该校六年级参赛学生得分总和一定是偶数。

例12某学校一年级一班共有25名同学，教室座位恰好排成5行，每行5个座位.把每一个座位的前、后、左、右的座位叫做原座位的邻位.问：让这25个学生都离开原座位坐到原座位的邻位，是否可行？例13在中国象棋盘任意取定的一个位置上放置着一颗棋子“马”，按中国象棋的走法，当棋盘上没有其他棋子时，这只“马”跳了若干步后回到原处，问：“马”所跳的步数是奇数还是偶数？例14线段AB有两个端点，一个端点染红色，另一个端点染蓝色.在这个AB 线段中间插入n个交点，或染红色，或染蓝色，得到n＋1条小线段（不重叠的线段）.试证：两个端点例外色的小线段的条数一定是奇数。

奇数、偶数与奇偶分析整数按能否被2整除分为两大类：奇数和偶数，奇数与偶数有下列基本性质：1．奇数≠偶数2．两个整数相加(减)或相乘，结果的奇偶性如下表所示3．若干个奇数之积是奇数，偶数与任意整数之积是偶数；偶数个奇数的和为偶数，若干个偶数的和为偶数．4．设m、n是整数，则m土n，nm±的奇偶性相同．5．设m是整数，则m与m，m n的奇偶性相同．奇偶性是整数的固有属性，通过分析整数的奇偶性来解决问题的方法叫奇偶分析法．例题【例1】三个质数之和为86，那么这三个质数是．思路点拨运用奇数、偶数、质数、合数性质，从分析三个加数的奇偶性人手．注：18世纪的哥尼斯堡，有7座桥把这儿的普雷格尔河中两个小岛与河岸联系起来，在这迷人的地方，人们议论着一个有趣的问题．一个游人怎样才能不重复地一次走遍7座桥，而最后又回到出发点．1736年彼得堡院士欧拉巧妙地解决了这个问题．欧拉把一个复杂的实际问题化为一个简单的几何图形，他指出只要我们能从一点出发，不重复地一笔把这样的图形画出来，那么就可说明游人能够不重复地一次走遍这7座桥，这就是著名的“一笔画”问题的来历．利用奇偶分析不难得到一般的结论：凡是能一笔画成的图形，它上面除了起点和终点外的每一个点总是一笔进来，一笔出去．因此，除了起点和终点外的每一个点都有偶数条线和它相连．简单地说，当且仅当图形中的奇结点(每点出发有奇数字线)的个数不大于2时，这个图形才能一笔画．【例2】如果a、b、c是三个任意的整数，那么222accbba+++、、（）．A．都不是整数B．至少有两个整数C．至少有一个整数D．都是整数思路点拨举例验证或从a、b、c的奇偶性说明．【例3】(1)设1，2，3，…，9的任一排列为a l，a2，a3…，a9．求证：(a l l一1)( a2—2)…(a9—9)是一个偶数．(2)在数11，22，33，44，54，…20022002，20032003，这些数的前面任意放置“+”或“一”号，并顺次完成所指出的运算，求出代数和，证明：这个代数和必定不等于2003．思路点拨(1)转换角度考察问题，化积的奇偶性为和的奇偶性来研究；(2)由于任意添“十”号或“一”号，形式多样，因此不可能一一尝试再作解答，从奇数、偶数的性质人手．【例4】已知n x x x x 、、、、Λ321都是+1或一1，并且011433221=+++++-x x x x x x x x x x n n n Λ，求证：n 是4的倍数．思路点拨 可以分两步，先证n 是偶数2k ，再证明k 是偶数，解题的关键是从已知等式左边各项的特点受到启发，挖掘隐含的一个等式．【例5】 游戏机的“方块”中共有下面?种图形．每种“方块”都由4个l ×l 的小方格组成．现用这7种图形拼成一个7× 4的长方形(可以重复使用某些图形)．问：最多可以用这7种图形中的几种图形?思路点拨 为了形象化地说明问题，对7×4的长方形的28个小方格黑白相间染色，除“品字型”必占3个黑格1个白格或3个白格1个黑格，其余6个方格各占2个黑格2个白格．注：对同一个数学对象，从两个方向考虑(n 项和与积)，再将这两个方面合在一起整体考虑，得出结论，这叫计算两次原理，通过计算两次可以建立方程，证明恒等式等．在一定的规则下，进行某种操作或变换，问是否(或证明)能够达到一个预期的目的，这就是所谓操作变换问题，此类问题变化多样，解法灵活，解题的关键是在操作变换中，挖掘不变量，不变性．一些非常规数字问题需要恰当地数学化，以便计算或推理．引入字母与赋值法是数学化的两种常用方式方法．所谓赋值法就是在解题时，将问题中的某些元素用适当的数表示，然后利用这些数值的大小，正负性、奇偶性等进行推理论证的一种解题方法．【例6】桌上放着七只杯子；杯口全朝上，每次翻转四个杯子：问能否经过若干次这样的翻动，使全部的杯子口都朝下?思路点拨 这不可能．我们将口向上的杯于记为：“0”，口向下的杯子记为“1”．开始时，由于七个杯子全朝上，所以这七个数的和为0，是个偶数．一个杯子每翻动一次，所记数由0变为1，或由l 变为0，改变了奇偶性．每一次翻动四个杯子，因此，七个之和的奇偶性仍与原来相同．所以，不论翻动多少次，七个数之和仍为偶数．而七个杯子全部朝下，和为7，是奇数，因此，不可能．整数可以分为奇数和偶数两类．【例7】在1，2，3，…，2005前面任意添上一个正号或负号，它们的代数和是奇数还是偶数?思路点拨 两个整数之和与这两个整数之差的奇偶性相同，只要知道1+2+3+…+2005的奇偶性即可．因两个整数的和与差的奇偶性相同，所以，在1，2，3，…，2005中每个数前面添上正号或负号，其代数和应与1+2+3+…+2005的奇偶性相同，而1+2+3+…+2005=21(1+ 2005)×2005=1003 ×2005为奇数；因此，所求代数和为奇数．注：抓住“a+b 与a —b 奇偶性相同”，通过特例1十2十3十…十2005得到答案．【例8】“ 元旦联欢会上，同学们互赠贺卡表示新年的：良好祝愿．“无论人数是什么数，用来交换的贺卡的张数总是偶数．”这句话正确吗?试证明你的结论．思路点拨 用分类讨论的思想方法，从“无论人数是什么数”入手，考虑人数为奇数或偶数的两种情况．这句话是正确的．下面证明之．若联欢会上的人数为偶数，设为2m (m 为整数)，则每个人赠送给同学们的贺卡张数为奇数，即(2m —1)．那么，贺卡总张数为2m(2m —1)=4m 2-2m ，显然是偶数．若联欢会上的人数为奇数，设为2m+1(m 为整数，则每个人赠送给同学们的贺卡张数应是2m ，为偶数．贺卡总张数为(2m+1)·2m ，仍为偶数．故“用来交换的贺卡张数总是偶数”是对的．注：按奇数和偶数分类考虑问题是常见的解决此类问题的策略之一．【例9】桌面上放有1993枚硬币，第1次翻动1993枚，第2次翻动其中的1992枚，第3次翻动其中的1991枚，…，第1993次翻动其中一枚，试问：能否使桌面上所有的1993枚硬币原先朝下的一面都朝上?并说明理由．思路点拨 若要把一枚硬币原先朝下的一面朝上，应该翻动该硬币奇数次．因此，要把1993枚硬币原先朝下的一面都朝上，应该翻动这1993枚硬币的总次数为奇数．现在1993次翻动的总次数为1+2+3+…+1993=1993×(1+1993)/2=1993×997是个奇数，故猜想可以使桌面上1993枚硬币原先朝下的一面都朝上．理由如下：按规定，1993次翻动的总次数为1+2+3+…+1993=1993×(1+1993)/2=1993×997，所以翻动的次数为奇数，而且可见每个硬币平均翻动了997次．而事实上，只要翻动一枚硬币奇数次，就能使这枚硬币原先朝下的一面朝上．按如下的方法进行翻动： 第1次翻动全部1993枚，第2次翻动其中的1992枚，第1993次翻动第2次未翻动的那1枚，第3次翻动其中的1991枚，第1992次翻动第3次未翻动的2枚，第997次翻动其中的997枚，第998次翻动第997次未翻动的996枚．这样，正好每枚硬币被翻动了997次，就能使每一枚硬币原来朝下的一面都朝上． 注：灵活、巧妙地利用奇俩性分析推理，可以解决许多复杂而有趣的问题，并有意想不到的效果．【例10】在6张纸片的正面分别写上整数：1、2、3、4、5、6，打乱次序后，将纸片翻过来，在它们的反面也随意分别写上1-6这6个整数，然后，计算每张纸片的正面与反面所写数字之差的绝对值，得出6个数．请你证明：所得的6个数中至少有两个是相同的． 思路点拨 从反面人手，即设这6个数两两都不相等，利用bi a i -与i i b a - (i =1，2，3，4，5，6)的奇偶性相同，引入字母进行推理证明．设6张卡片正面写的数是654321a a a a a a 、、、、、，反面写的数对应为654321b b b b b b 、、、、、，则这6张卡片正面写的数与反面写的数的绝对值分别为11b a -，22b a -，33b a -，44b a -，55b a -，66b a -．设这6个数两两都不相等，则它们只能取0，1，2，3，4，5这6个值．于是11b a -+22b a -+33b a -+44b a -+55b a -+66b a -=0+1+2+3+4+5=15是个奇数． 另一方面，bi a i -与i i b a - (i =1，2，3，4，5，6)的奇偶性相同．所以11b a -+22b a -+33b a -+44b a -+55b a -+66b a -与(a 1一b 1)+(a 2一b 2)+(a 3一b 3)+(a 4一b 4)+(a 5一b 5)+(a 6一b 6)= )(654321a a a a a a +++++一)(654321b b b b b b +++++ =(1+2+3+4+5+6)一(1+2+3+4+5+6)=O 的奇偶性相同，而0是个偶数，15是奇数，两者矛盾．所以，11b a -，22b a -，33b a -，44b a -，55b a -，66b a -这6个数中至少有两个是相同的．注：反证法是解决奇、偶数问题中常用的方法．【例11】有一只小渡船往返于一条小河的左右两岸之间，问：(1)若最初小船是在左岸，往返若干次后，它又回到左岸，那么这只小船过河的次数是奇数还是偶数?如果它最后到了右岸，情况又是怎样呢?(2)若小船最初在左岸，它过河99次之后，是停在左岸还是右岸?思路点拨 (1)小船最初在左岸，过一次河就到了右岸，再过一次河就由右岸回到左岸，即每次由左岸出发到右岸后再回到左岸，都过了两次河．因此，小船由左岸开始，往返多次后又回到左岸，则过河的次数必为2的倍数，所以是偶数．同样的道理，不难得出，若小船最后停在右岸，则过河的次数必为奇数．(2)通过(1)，我们发现，若小船最初在左岸，过偶数次河后，就回到左岸；过奇数次河后，就停在右岸．现在小船过河99次，是奇数次．因此，最后小船该停在右岸．注 关键是对过河次数的理解：一个单程，即由左岸到右岸(或由右岸到左岸)就过河一次；往返一个来回就过河两次．【例12】黑板上写了三个整数，任意擦去其中一个，把它改写成另两个数的和减去1，这样继续下去，得到1995、1996、1997，问原来的三个数能否是2、2、2？思路点拨 如果原来的三个整数是2、2、2，即三个偶数，操作一次后，三个数变成二偶一奇，这时如果擦去其中的奇数，操作后三个数仍是二偶一奇．如果擦去的是其中的一个偶数，操作后三个数仍是二偶一奇．因此，无论怎样操作，得到的三个数都是二偶一奇，不可能得到1995、1996、1997．所以，原来的三个数不可能是2、2、2．注 解决本题的诀窍在于考查数字变化后的奇偶性．【例13】将正偶数按下表排成五列：第1列 第2列 第3列 第4列 第5列第1行 2 4 6 8第2行 16 14 12 10第3行 18 20 22 24… … 28 26根据上面的排列规律，则2000应位于( )A ．第125行，第1列B ．第125行，第2列C ．第250行，第1列D ．第250行，第2列思路点拨 观察表格，第1行最右边的数为8，第2行最左边的数为16，第3行最右边的数为24，于是可猜测：当行数为奇数时，该行最右边的数为8×行数；当行数为偶数时，该行最左边的数为8×行数．通过验证第4行、第5行、第6行知，上述猜想是正确的，因为2000=8×250，所以2000应在第250行，又因为250为偶数，故2000应在第250行最左边，即第250行第1列，故应选C ．注：观察、寻找规律是解决这类问题的妙招．【例14】如图18—1，两个标有数字的轮子可以分别绕轮子的中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字．若左轮子上方的箭头指着的数字为a ，右轮子上方的箭头指着的数字为b ，数对(a ，b)所有可能的个数为n ，其中a+b 恰为偶数的不同数对的个数为m ，则nm 等于( ) A ．21 B ．61 C ．125 D ．43 思路点拨 依题意可知所有的数对n=4×3=12，其中a+b 恰为偶数的数对m=3×1+1×2=5．因此，n m =125，故选C ． 【例15】已知a 、b 、c 中有两个奇数、一个偶数，n 是整数，如果S=(a+2n+1)(b+2n 十2)(c+2n 十3)，那么( )A ．S 是偶数B ．S 是奇数C ．S 的奇偶性与n 的奇偶性相同D ． S 的奇偶性不能确定思路点拨 弄清a+2n+1，b+2n+2，c+2n+3的奇偶性即可．依题得：(a+2n+1)+(b+2n+2)+(c+2n+3)=a+b+c+6(n+1)．∵a+b+c 为偶数，6(n+1)为偶数，∴a+b+c+6(n+1)为偶数∴a+2n+1，b+2n+2，c+2n+3中至少有一个为偶数，∴S 是偶数．故选A ．注：三个数的和为偶数，则至少有一个为偶数；三个数中有一个为偶数，则三数之和为偶数．学力训练 1．若按奇偶性分类，则12+22+32+…+20022002是 数．2．能不能在下式， 的各个方 框中分别填人“+”号或“一”号，使等式成立?答： ．3．已知三个质数a 、b 、c 满足a+b+c+abc ＝99，那么a c c b b a -+-+-的值等于 ．4．已知n 为整数，现有两个代数式：(1)2n+3，(2)4n 一1，其中，能表示“任意奇数”的( )A ．只有(1)B ．只有(2)C ．有(1)和(2)D ．一个也没有5．如果a ，b ，c 都是正整数，且a ，b 是奇数，则3a +(b 一1)2c 是( )．A ．只当c 为奇数时，其值为奇数B ．只当c 为偶数时，其值为奇数C ．只当c 为3的倍数，其值为奇数D ．无论c 为任何正楚数，其值均为奇数6．已知a ，b ，c 三个数中有两个奇数、一个偶数，n 是整数，如果S=(a+n+1)(b+ 2n+2)(c+3n+3)，那么( )．A ． S 是偶数B ．S 是奇数C ．S 的奇偶性与n 的奇偶性相同D ．S 的奇偶性不能确定7．(1)是否有满足方程x 2－y 2=1998的整数解x 和y?如果有，求出方程的解；如果没有，说明理由．(2)一个立方体的顶点标上+1或一1，面上标上一个数，它等于这个面的4个顶点处的数的乘积，这样所标的14个数的和能否为0?8．甲、乙两人玩纸牌游戏，甲持有全部的红桃牌(A 作1，J ，Q ，K 分别作11，12，13，不同)，乙持有全部的黑桃牌，两人轮流出牌，每次出一张，得到一对牌，出完为止，共得到13对牌，每对牌彼此相减，问这13个差的乘积的奇偶性能否确定?9．在1，2，3，…,1998之前任意添上“十”或“一”号，然后相加，这些和中最小的正整数是 ．10．1，2，3，…，98共98个自然数，能够表示成两整数平方差的数的个数是 ．11．在一次象棋比赛中，每两个选手恰好比赛一局，每局赢者记2分，输者记0分，平局每个选手各记1分，今有4个人统计百这次比赛中全部得分总数，由于有的人粗心，其数据各不相同，分别为1979，1980，1984，1985，经核实，其中有一人统计无误，则这次比赛共有 名选手参加．12．已知p 、q 、pq+1都是质数，且p 一q>40，那么满足上述条件的最小质数p ＝ ； q ＝ ．13．设a ，b 为整数，给出下列4个结论(1)若a+5b 是偶数，则a 一3b 是偶数；(2)若a 十5b 是偶数，则a 一3b 是奇数；(3)若a+5b 是奇数，则a 一3b 是偶数；(4)若a+5b 是奇数，则a 一3b 是奇数，其中结论正确的个数是( )．A ．0个B ．2个C ．4个D ． 1个或3个14．下面的图形，共有( )个可以一笔画(不重复也不遗漏；下笔后笔不能离开纸) ．A ．0B ．1C ．2D ．315．π的前24位数值为3.14159265358979323846264…，在这24个数字中，随意地逐个抽取1个数字，并依次记作a1，a2，…a24，则(a1一a2)( a3一a4)…(a23一a24)为( )．A．奇数B．偶数C．奇数或偶数D．质数16.没标有A、B、C、D、C、F、G记号的7盏灯顺次排成一行，每盏灯安装一个开关，现在A、C、E、G 4盏灯开着，其余3盏灯是关的，小刚从灯A开始，顺次拉动开关，即从A 到G，再从A始顺次拉动开关，即又从A到G…，他这样拉动了1999次开关后，问哪几盏是开的?17．有1997枚硬币，其中1000枚国徽朝上，997枚国徽朝下．现要求每一次翻转其中任意6枚，使它们的国徽朝向相反，问能否经过有限次翻转之后，使所有硬币的国徽都朝上?给出你的结论，并给予证明．18．对一个正整数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到1时操作停止，求经过9次操作变为l的数有多少个？19．高为50cm，底面周长为50cm的圆柱，在此圆柱的侧面上划分(如图所示)边长为lcm的正方形，用四个边长为lcm的小正方形构成“T”字形，用此图形是否能拼成圆柱侧面?试说明理由．参考答案。

奥数奇数和偶数知识要点：奇数和偶数的概念：整数可以分成奇数和偶数两大类。

能被2整除的数叫做偶数（双数），不能被2整除的数叫做奇数（单数）。

特别注意，因为0能被2整除，所以0是偶数。

因此最小的奇数是１，最小的偶数是0。

1、偶数与奇数的关系：偶数＋偶数=（）偶数－偶数=（）偶数＋奇数=（）偶数－奇数=（）奇数＋奇数=（）奇数－奇数=（）偶数×偶数=（）偶数×奇数=（）奇数×奇数=（）偶数÷偶数=（）偶数÷奇数=（）奇数÷奇数=（）2、奇数个奇数的和等于奇数，偶数个奇数的和等于偶数，任意个偶数的和等于偶数。

3、任意个奇数的积等于奇数，偶数与任意自然数之积是偶数。

4、若干个自然数的积是奇数，则每一个乘数都是奇数；若干个自然数之积是偶数，则其中必定有一个乘数是偶数。

5、相邻的两个整数必为一奇一偶，它们的积必为偶数，它们的和必为奇数。

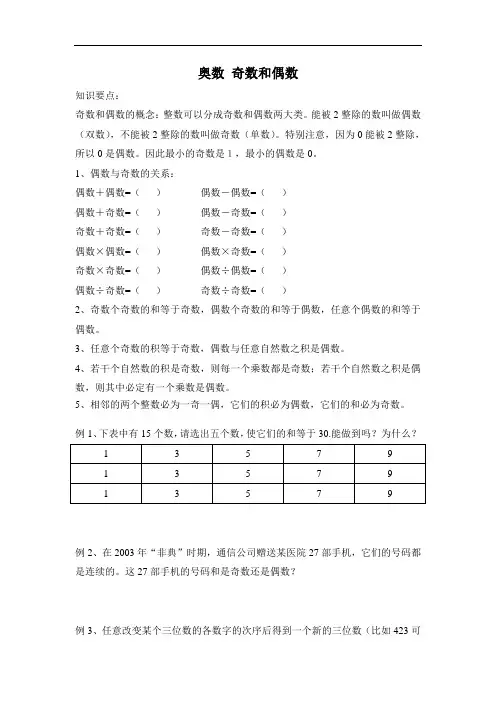
例1、下表中有15个数，请选出五个数，使它们的和等于30.能做到吗？为什么？例2、在2003年“非典”时期，通信公司赠送某医院27部手机，它们的号码都是连续的。

这27部手机的号码和是奇数还是偶数？例3、任意改变某个三位数的各数字的次序后得到一个新的三位数（比如423可改变为432、342等），试问这个新的三位数与原来的那个三位数的和能不能等于999？如果能，试举一例；如果不能，请说明理由。

例4、赵老师在黑板上写了三个整数。

然后擦去一个数，再写上其他两个数之和；然后再随意擦去一个数，再写出其他两个数之和。

就这样一直做下去，最后得到2004,2005,2006。

赵老师一开始写的三个数有没有可能是1,3,5？例5、张老师在黑板上依次写下0,1,3,8,21，…一列数，规律是：每个数的3倍等于它前后相邻的两个数字的和，那么张老师写的第20个数是奇数还是偶数？例6、a,b,c,d是四个不同的质数，且a﹢b﹢c＝d,那么a×b×c×d的积最小是多少？例7、已知a,b,c是三个连续的自然数，其中a是偶数，小红和小明两人的说法正确的是（）小红：那么﹙a＋1﹚, ﹙b＋2﹚, ﹙c＋3﹚这三个数的乘积一定是奇数。

奇数和偶数1．1+2+3+4+…+100+101是奇数还是偶数？2．在30到100中所有3的倍数的和是奇数还是偶数？3．有一列数：1，1，2，3，5，8，13，21，34，55，…，从第三个数开始，每个数都是前两个数的和．那么在前1000个数中，有多少个奇数？4．扑克牌中的J、Q、K分别表示11、12、13．甲取13张红心，乙取13张草花，两人都各自任意出一张牌凑成一对，这样一共可凑成13对．如果将每对求和，再将这13个和相乘，从积的奇偶性看，积应是____数．5．算式1×2+3×4+5×6+…+99×100的得数是奇数还是偶数？6．若一个能被5整除的两位数既不能被3整除，又不能被4整除，它的97倍是偶数，十位数字不小于6，则这个两位数是几？（第九届“希望杯”全国数学邀请赛第2试第4题）7．能否在下面的口内填人加号或减号，使得等式成立？为什么？1口2口3口4口5口6口7口8口9=IO8．算式1×2+3×4+5×6+…+99×100的得数是奇数还是偶数？9．若一个能被5整除的两位数既不能被3整除，又不能被4整除，它的97倍是偶数，十位数字不小于6，则这个两位数是几？（第九届“希望杯”全国数学邀请赛第2试第4题）10．能否在下面的口内填人加号或减号，使得等式成立？为什么？1口2口3口4口5口6口7口8口9=IO11．三个连续奇数的和是201，求这三个奇数．12．99+98 - 97+96 -95+…+2-1足奇数还是偶数？说明你的理由，13．已知三个整数a、b、c的和是奇数，并且a-b=3，那么a、b、c的奇偶性为( )．(A)三个都是奇数 (B)两个奇数一个偶数(C)一个奇数两个偶数 (D)三个都是偶数14．计算前100个正整数中所有奇数的和与所有偶数的和，从3，15，9，7，21，1，5，11，7中挑出7个数，使它们的和为50．能不能做到？说说你是怎么想的．15．用1，2，3，4，5这五个数两两相乘，可以得到10个不同的乘积．问乘积中是偶数多还是奇数多？16．在黑板上写3个整数，然后擦去一个换成其他两数之和或者差，这样继续操作下去，最后得到64，78，142.问：原来写的3个整数能否为1，3，57。

五年级上册奥数奇数与偶数及奇偶性的应用(例题含答案)第五讲：奇数与偶数及奇偶性的应用一、基本概念和知识1.奇数和偶数整数可以分为奇数和偶数两类。

能被2整除的数为偶数，不能被2整除的数为奇数。

偶数可表示为2k（k为整数），奇数可表示为2k+1（k为整数）。

需要注意的是，因为能被2整除，所以是偶数。

2.奇数与偶数的运算性质性质1：偶数±偶数=偶数，奇数±奇数=偶数。

性质2：偶数±奇数=奇数。

性质3：偶数个奇数相加得偶数。

性质4：奇数个奇数相加得奇数。

性质5：偶数×奇数=偶数，奇数×奇数=奇数。

二、例题利用奇数与偶数的性质，可以解决许多实际问题。

例如，求1+2+3+…+1993的和是奇数还是偶数？可以利用高斯求和公式直接求出和，再判别和的奇偶性。

但是，从加数的奇偶性考虑，同样可以判断和的奇偶性。

此题有两种解法。

解法1：因为997和1993是奇数，奇数×奇数=奇数，所以原式的和是奇数。

解法2：1～1993的自然数中，有996个偶数和997个奇数。

因为996个偶数之和一定是偶数，又因为奇数个奇数之和是奇数，所以997个奇数之和是奇数。

因为偶数+奇数=奇数，所以原式之和一定是奇数。

还有一个例题：一个数分别与另外两个相邻奇数相乘，所得的两个积相差150，这个数是多少？可以有两种解法。

解法1：因为相邻两个奇数相差2，所以150是这个数的2倍。

所以这个数是150÷2=75.解法2：设这个数为x，设相邻的两个奇数为2a+1和2a-1（a≥1）。

则有（2a+1）x-（2a-1）x=150，化简得2x=150，所以这个要求的数是75.最后一个例题：元旦前夕，同学们相互送贺年卡。

每人只要接到对方贺年卡就一定回赠贺年卡，那么送了奇数张贺年卡的人数是奇数还是偶数？为什么？解：因为是两人互送贺年卡，给每人分别标记送出贺年卡一次。

那么贺年卡的总张数应能被2整除，所以XXX的总张数应是偶数。

5-1奇數與偶數的性質與應用教學目標本講知識點屬於數論大板塊內的“定性分析”部分，小學生的數學思維模式大多為“純粹的定量計算，拿到一個題就先去試數，或者是找規律，在性質分析層面幾乎為0，本講力求實現的一個主要目標是提高孩子對數學的嚴密分析能力，培養孩子明白做題前有時要“先看能不能這麼做，再去動手做”的思維模式。

無論是小升初還是杯賽會經常遇到，但不會單獨出題，而是結合其他知識點來考察學生綜合能力。

知識點撥一、奇數和偶數的定義整數可以分成奇數和偶數兩大類.能被2整除的數叫做偶數，不能被2整除的數叫做奇數。

通常偶數可以用2k（k為整數）表示，奇數則可以用2k+1（k 為整數）表示。

特別注意，因為0能被2整除，所以0是偶數。

二、奇數與偶數的運算性質性質1：偶數±偶數=偶數，奇數±奇數=偶數性質2：偶數±奇數=奇數性質3：偶數個奇數的和或差是偶數性質4：奇數個奇數的和或差是奇數性質5：偶數×奇數=偶數，奇數×奇數=奇數，偶數×偶數=偶數三、兩個實用的推論推論1：在加減法中偶數不改變運算結果奇偶性，奇數改變運算結果的奇偶性。

推論2：對於任意2個整數a,b ,有a+b與a-b同奇或同偶例題精講模組一、奇偶分析法之計算法【例 1】1231993++++……的和是奇數還是偶數？【例 1】從1開始的前2005個整數的和是______數(填：“奇”或“偶”)。

【巩固】2930318788+++++……得數是奇數還是偶數？【巩固】123456799100999897967654321+++++++++++++++++++++的和是奇數還是偶數？為什麼？【巩固】(200201202288151152153233……）（……）得數是奇數還是偶數？++++-++++【例 2】12345679899+⨯+⨯+⨯++⨯的計算結果是奇數還是偶數，為什麼？【例 3】東東在做算術題時，寫出了如下一個等式：1038137564=⨯+，他做得對嗎？【例 4】一個自然數分別與另外兩個相鄰奇數相乘，所得的兩個積相差150，那麼這個數是多少？【巩固】一個偶數分別與其相鄰的兩個偶數相乘，所得的兩個乘積相差80，那麼這三個偶數的和是多少？【例 5】能否在下式的“□”內填入加號或減號，使等式成立，若能請填入符號，不能請說明理由。

奥数《奇偶问题》微课（教案）人教版数学四年级上册一、教学目标1. 让学生掌握奇数和偶数的概念，能够正确区分奇数和偶数。

2. 培养学生运用奇偶性解决实际问题的能力，提高学生的逻辑思维能力。

3. 激发学生对数学的兴趣，培养学生主动探索、合作交流的学习习惯。

二、教学内容1. 奇数和偶数的概念2. 奇数和偶数的性质3. 奇偶性在实际问题中的应用三、教学重点与难点1. 教学重点：奇数和偶数的概念，奇数和偶数的性质。

2. 教学难点：奇偶性在实际问题中的应用。

四、教学过程1. 导入新课利用生活中的实例，如：桌子上的苹果，让学生观察苹果的数量，引导学生发现苹果数量是偶数，激发学生对奇偶问题的兴趣。

2. 探究新知（1）让学生举例说明生活中的奇数和偶数。

（2）引导学生观察奇数和偶数的特征，总结出奇数和偶数的定义。

（3）让学生举例说明奇数和偶数的性质，如：奇数加奇数等于偶数，奇数乘奇数等于奇数等。

3. 实践应用（1）让学生解决实际问题，如：小明有10个苹果，他想把这些苹果分成两组，每组苹果的数量都是奇数或偶数，请问他有几种分法？（2）让学生通过小组合作，探讨奇偶性在实际问题中的应用，如：在游戏中，如何利用奇偶性来判断胜负？4. 总结提升引导学生回顾本节课所学内容，总结奇数和偶数的概念、性质以及在实际问题中的应用。

五、课后作业1. 判断下列数中，哪些是奇数，哪些是偶数：13、24、57、100、145。

2. 小明有15个苹果，他想把这些苹果分成若干组，每组苹果的数量都是奇数，请问他有几种分法？3. 请你举例说明在生活中，奇偶性是如何应用的？六、板书设计1. 奇数和偶数的概念2. 奇数和偶数的性质3. 奇偶性在实际问题中的应用七、教学反思本节课通过生活中的实例，引导学生探究奇数和偶数的概念和性质，让学生在实际问题中运用奇偶性，培养学生的逻辑思维能力。

在教学过程中，要注意关注学生的学习情况，及时给予指导和鼓励，让学生在轻松愉快的氛围中学习数学。

四年级奥数讲义:奇数、偶数与奇偶分析整数按能否被2整除分为两大类:奇数和偶数，奇数与偶数有下列基本性质:1．奇数≠偶数2．两个整数相加(减)或相乘，结果的奇偶性如下表所示3．若干个奇数之积是奇数，偶数与任意整数之积是偶数；偶数个奇数的和为偶数，若干个偶数的和为偶数．m 的奇偶性相同．4．设m、n是整数，则m土n，n5．设m是整数，则m与m，m n的奇偶性相同．奇偶性是整数的固有属性，通过分析整数的奇偶性来解决问题的方法叫奇偶分析法．例题【例1】三个质数之和为86，那么这三个质数是．思路点拨运用奇数、偶数、质数、合数性质，从分析三个加数的奇偶性人手．注: 18世纪的哥尼斯堡，有7座桥把这儿的普雷格尔河中两个小岛与河岸联系起来，在这迷人的地方，人们议论着一个有趣的问题．一个游人怎样才能不重复地一次走遍7座桥，而最后又回到出发点．1736年彼得堡院士欧拉巧妙地解决了这个问题．欧拉把一个复杂的实际问题化为一个简单的几何图形，他指出只要我们能从一点出发，不重复地一笔把这样的图形画出来，那么就可说明游人能够不重复地一次走遍这7座桥，这就是著名的“一笔画”问题的来历．利用奇偶分析不难得到一般的结论:凡是能一笔画成的图形，它上面除了起点和终点外的每一个点总是一笔进来，一笔出去．因此，除了起点和终点外的每一个点都有偶数条线和它相连．简单地说，当且仅当图形中的奇结点(每点出发有奇数字线)的个数不大于2时，这个图形才能一笔画．【例2】 如果a 、b 、c 是三个任意的整数，那么222a c c b b a +++、、（ ）． A ．都不是整数 B ．至少有两个整数 C ．至少有一个整数 D ．都是整数思路点拨 举例验证或从a 、b 、c 的奇偶性说明．【例3】 (1)设1，2，3，…，9的任一排列为a l ，a 2，a 3…，a 9．求证:(a l l 一1)( a 2 —2)…(a 9—9)是一个偶数．(2)在数11，22，33，44，54，…20022002，20032003，这些数的前面任意放置“+”或“一”号，并顺次完成所指出的运算，求出代数和，证明:这个代数和必定不等于2003．思路点拨 (1)转换角度考察问题，化积的奇偶性为和的奇偶性来研究；(2)由于任意添“十”号或“一”号，形式多样，因此不可能一一尝试再作解答，从奇数、偶数的性质人手．【例4】已知n x x x x 、、、、 321都是+1或一1，并且011433221=+++++-x x x x x x x x x x n n n ，求证:n 是4的倍数．思路点拨 可以分两步，先证n 是偶数2k ，再证明k 是偶数，解题的关键是从已知等式左边各项的特点受到启发，挖掘隐含的一个等式．【例5】 游戏机的“方块”中共有下面?种图形．每种“方块”都由4个l ×l 的小方格组成．现用这7种图形拼成一个7× 4的长方形(可以重复使用某些图形)．问:最多可以用这7种图形中的几种图形?思路点拨 为了形象化地说明问题，对7×4的长方形的28个小方格黑白相间染色，除“品字型”必占3个黑格1个白格或3个白格1个黑格，其余6个方格各占2个黑格2个白格．注:对同一个数学对象，从两个方向考虑(n 项和与积)，再将这两个方面合在一起整体考虑，得出结论，这叫计算两次原理，通过计算两次可以建立方程，证明恒等式等．在一定的规则下，进行某种操作或变换，问是否(或证明)能够达到一个预期的目的，这就是所谓操作变换问题，此类问题变化多样，解法灵活，解题的关键是在操作变换中，挖掘不变量，不变性．一些非常规数字问题需要恰当地数学化，以便计算或推理．引入字母与赋值法是数学化的两种常用方式方法．所谓赋值法就是在解题时，将问题中的某些元素用适当的数表示，然后利用这些数值的大小，正负性、奇偶性等进行推理论证的一种解题方法．【例6】桌上放着七只杯子；杯口全朝上，每次翻转四个杯子:问能否经过若干次这样的翻动，使全部的杯子口都朝下?思路点拨 这不可能．我们将口向上的杯于记为:“0”，口向下的杯子记为“1”．开始时，由于七个杯子全朝上，所以这七个数的和为0，是个偶数．一个杯子每翻动一次，所记数由0变为1，或由l 变为0，改变了奇偶性．每一次翻动四个杯子，因此，七个之和的奇偶性仍与原来相同．所以，不论翻动多少次，七个数之和仍为偶数．而七个杯子全部朝下，和为7，是奇数，因此，不可能．整数可以分为奇数和偶数两类．【例7】在1，2，3，…，2005前面任意添上一个正号或负号，它们的代数和是奇数还是偶数?思路点拨 两个整数之和与这两个整数之差的奇偶性相同，只要知道1+2+3+…+2005的奇偶性即可．因两个整数的和与差的奇偶性相同，所以，在1，2，3，...，2005中每个数前面添上正号或负号，其代数和应与1+2+3+...+2005的奇偶性相同，而1+2+3+ (2005)21(1+ 2005)×2005=1003 ×2005为奇数；因此，所求代数和为奇数．注:抓住“a+b 与a —b 奇偶性相同”，通过特例1十2十3十…十2005得到答案．【例8】“ 元旦联欢会上，同学们互赠贺卡表示新年的:良好祝愿．“无论人数是什么数，用来交换的贺卡的张数总是偶数．”这句话正确吗?试证明你的结论．思路点拨 用分类讨论的思想方法，从“无论人数是什么数”入手，考虑人数为奇数或偶数的两种情况．这句话是正确的．下面证明之．若联欢会上的人数为偶数，设为2m (m 为整数)，则每个人赠送给同学们的贺卡张数为奇数，即(2m —1)．那么，贺卡总张数为2m(2m —1)=4m 2-2m ，显然是偶数．若联欢会上的人数为奇数，设为2m+1(m 为整数，则每个人赠送给同学们的贺卡张数应是2m ，为偶数．贺卡总张数为(2m+1)·2m ，仍为偶数．故“用来交换的贺卡张数总是偶数”是对的．注:按奇数和偶数分类考虑问题是常见的解决此类问题的策略之一．【例9】桌面上放有1993枚硬币，第1次翻动1993枚，第2次翻动其中的1992枚，第3次翻动其中的1991枚，…，第1993次翻动其中一枚，试问:能否使桌面上所有的1993枚硬币原先朝下的一面都朝上?并说明理由．思路点拨 若要把一枚硬币原先朝下的一面朝上，应该翻动该硬币奇数次．因此，要把1993枚硬币原先朝下的一面都朝上，应该翻动这1993枚硬币的总次数为奇数．现在1993次翻动的总次数为1+2+3+…+1993=1993×(1+1993)/2=1993×997是个奇数，故猜想可以使桌面上1993枚硬币原先朝下的一面都朝上．理由如下:按规定，1993次翻动的总次数为1+2+3+…+1993=1993×(1+1993)/2=1993×997，所以翻动的次数为奇数，而且可见每个硬币平均翻动了997次．而事实上，只要翻动一枚硬币奇数次，就能使这枚硬币原先朝下的一面朝上．按如下的方法进行翻动:第1次翻动全部1993枚，第2次翻动其中的1992枚，第1993次翻动第2次未翻动的那1枚，第3次翻动其中的1991枚，第1992次翻动第3次未翻动的2枚，第997次翻动其中的997枚，第998次翻动第997次未翻动的996枚．这样，正好每枚硬币被翻动了997次，就能使每一枚硬币原来朝下的一面都朝上．注:灵活、巧妙地利用奇俩性分析推理，可以解决许多复杂而有趣的问题，并有意想不到的效果．【例10】在6张纸片的正面分别写上整数:1、2、3、4、5、6，打乱次序后，将纸片翻过来，在它们的反面也随意分别写上1-6这6个整数，然后，计算每张纸片的正面与反面所写数字之差的绝对值，得出6个数．请你证明:所得的6个数中至少有两个是相同的．思路点拨 从反面人手，即设这6个数两两都不相等，利用bi a i -与i i b a - (i =1，2，3，4，5，6)的奇偶性相同，引入字母进行推理证明．设6张卡片正面写的数是654321a a a a a a 、、、、、，反面写的数对应为654321b b b b b b 、、、、、，则这6张卡片正面写的数与反面写的数的绝对值分别为11b a -，22b a -，33b a -，44b a -，55b a -，66b a -．设这6个数两两都不相等，则它们只能取0，1，2，3，4，5这6个值．于是11b a -+22b a -+33b a -+44b a -+55b a -+66b a -=0+1+2+3+4+5=15是个 奇数． 另一方面，bi a i -与i i b a - (i =1，2，3，4，5，6)的奇偶性相同．所以11b a -+22b a -+33b a -+44b a -+55b a -+66b a -与(a 1一b 1)+(a 2一b 2)+(a 3一b 3)+(a 4一b 4)+(a 5一b 5)+(a 6一b 6)= )(654321a a a a a a +++++一)(654321b b b b b b +++++ =(1+2+3+4+5+6)一(1+2+3+4+5+6)=O 的奇偶性相同，而0是个偶数，15是奇数，两者矛盾．所以，11b a -，22b a -，33b a -，44b a -，55b a -，66b a -这6个数中至少有两个是相同的．注:反证法是解决奇、偶数问题中常用的方法．【例11】有一只小渡船往返于一条小河的左右两岸之间，问:(1)若最初小船是在左岸，往返若干次后，它又回到左岸，那么这只小船过河的次数是奇数还是偶数?如果它最后到了右岸，情况又是怎样呢?(2)若小船最初在左岸，它过河99次之后，是停在左岸还是右岸?思路点拨 (1)小船最初在左岸，过一次河就到了右岸，再过一次河就由右岸回到左岸，即每次由左岸出发到右岸后再回到左岸，都过了两次河．因此，小船由左岸开始，往返多次后又回到左岸，则过河的次数必为2的倍数，所以是偶数．同样的道理，不难得出，若小船最后停在右岸，则过河的次数必为奇数．(2)通过(1)，我们发现，若小船最初在左岸，过偶数次河后，就回到左岸；过奇数次河后，就停在右岸．现在小船过河99次，是奇数次．因此，最后小船该停在右岸．注 关键是对过河次数的理解:一个单程，即由左岸到右岸(或由右岸到左岸)就过河一次；往返一个来回就过河两次．【例12】黑板上写了三个整数，任意擦去其中一个，把它改写成另两个数的和减去1，这样继续下去，得到1995、1996、1997，问原来的三个数能否是2、2、2？思路点拨 如果原来的三个整数是2、2、2，即三个偶数，操作一次后，三个数变成二偶一奇，这时如果擦去其中的奇数，操作后三个数仍是二偶一奇．如果擦去的是其中的一个偶数，操作后三个数仍是二偶一奇．因此，无论怎样操作，得到的三个数都是二偶一奇，不可能得到1995、1996、1997．所以，原来的三个数不可能是2、2、2．注 解决本题的诀窍在于考查数字变化后的奇偶性．【例13】将正偶数按下表排成五列:第1列 第2列 第3列 第4列 第5列第1行 2 4 6 8第2行 16 14 12 10第3行 18 20 22 24… … 28 26根据上面的排列规律，则2000应位于( )A ．第125行，第1列B ．第125行，第2列C ．第250行，第1列D ．第250行，第2列思路点拨 观察表格，第1行最右边的数为8，第2行最左边的数为16，第3行最右边的数为24，于是可猜测:当行数为奇数时，该行最右边的数为8×行数；当行数为偶数时，该行最左边的数为8×行数．通过验证第4行、第5行、第6行知，上述猜想是正确的，因为2000=8×250，所以2000应在第250行，又因为250为偶数，故2000应在第250行最左边，即第250行第1列，故应选C ．注:观察、寻找规律是解决这类问题的妙招．【例14】如图18—1，两个标有数字的轮子可以分别绕轮子的中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字．若左轮子上方的箭头指着的数字为a ，右轮子上方的箭头指着的数字为b ，数对(a ，b)所有可能的个数为n ，其中a+b 恰为偶数的不同数对的个数为m ，则nm 等于( ) A ．21 B ．61 C ．125 D ．43 思路点拨 依题意可知所有的数对n=4×3=12，其中a+b 恰为偶数的数对m=3×1+1×2=5．因此，n m =125，故选C ．【例15】已知a、b、c中有两个奇数、一个偶数，n是整数，如果S=(a+2n+1)(b+2n十2)(c+2n十3)，那么( )A．S是偶数B．S是奇数C．S的奇偶性与n的奇偶性相同D．S的奇偶性不能确定思路点拨弄清a+2n+1，b+2n+2，c+2n+3的奇偶性即可．依题得:(a+2n+1)+(b+2n+2)+(c+2n+3)=a+b+c+6(n+1)．∵a+b+c为偶数，6(n+1)为偶数，∴a+b+c+6(n+1)为偶数∴a+2n+1，b+2n+2，c+2n+3中至少有一个为偶数，∴S是偶数．故选A．注:三个数的和为偶数，则至少有一个为偶数；三个数中有一个为偶数，则三数之和为偶数．学力训练 1．若按奇偶性分类，则12+22+32+…+20022002是 数．2．能不能在下式， 的各个方 框中分别填人“+”号或“一”号，使等式成立?答: ．3．已知三个质数a 、b 、c 满足a+b+c+abc ＝99，那么a c c b b a -+-+-的值等于 ．4．已知n 为整数，现有两个代数式:(1)2n+3，(2)4n 一1，其中，能表示“任意奇数”的( )A ．只有(1)B ．只有(2)C ．有(1)和(2)D ．一个也没有5．如果a ，b ，c 都是正整数，且a ，b 是奇数，则3a +(b 一1)2c 是( )．A ．只当c 为奇数时，其值为奇数B ．只当c 为偶数时，其值为奇数C ．只当c 为3的倍数，其值为奇数D ．无论c 为任何正楚数，其值均为奇数6．已知a ，b ，c 三个数中有两个奇数、一个偶数，n 是整数，如果S=(a+n+1)(b+ 2n+2)(c+3n+3)，那么( )．A ． S 是偶数B ．S 是奇数C ．S 的奇偶性与n 的奇偶性相同D ．S 的奇偶性不能确定7．(1)是否有满足方程x 2－y 2=1998的整数解x 和y?如果有，求出方程的解；如果没有，说明理由．(2)一个立方体的顶点标上+1或一1，面上标上一个数，它等于这个面的4个顶点处的数的乘积，这样所标的14个数的和能否为0?8．甲、乙两人玩纸牌游戏，甲持有全部的红桃牌(A 作1，J ，Q ，K 分别作11，12，13，不同)，乙持有全部的黑桃牌，两人轮流出牌，每次出一张，得到一对牌，出完为止，共得到13对牌，每对牌彼此相减，问这13个差的乘积的奇偶性能否确定?9．在1，2，3，…,1998之前任意添上“十”或“一”号，然后相加，这些和中最小的正整数是 ．10．1，2，3，…，98共98个自然数，能够表示成两整数平方差的数的个数是 ．11．在一次象棋比赛中，每两个选手恰好比赛一局，每局赢者记2分，输者记0分，平局每个选手各记1分，今有4个人统计百这次比赛中全部得分总数，由于有的人粗心，其数据各不相同，分别为1979，1980，1984，1985，经核实，其中有一人统计无误，则这次比赛共有名选手参加．12．已知p、q、pq+1都是质数，且p一q>40，那么满足上述条件的最小质数p＝；q＝．13．设a，b为整数，给出下列4个结论(1)若a+5b是偶数，则a一3b是偶数；(2)若a十5b是偶数，则a一3b是奇数；(3)若a+5b 是奇数，则a一3b是偶数；(4)若a+5b是奇数，则a一3b是奇数，其中结论正确的个数是( )．A．0个B．2个C．4个D．1个或3个14．下面的图形，共有( )个可以一笔画(不重复也不遗漏；下笔后笔不能离开纸) ．A．0 B．1 C ．2 D．315．π的前24位数值为3.14159265358979323846264…，在这24个数字中，随意地逐个抽取1个数字，并依次记作a1，a2，…a24，则(a1一a2)( a3一a4)…(a23一a24)为( )．A．奇数B．偶数C．奇数或偶数D．质数16.没标有A、B、C、D、C、F、G记号的7盏灯顺次排成一行，每盏灯安装一个开关，现在A、C、E、G 4盏灯开着，其余3盏灯是关的，小刚从灯A开始，顺次拉动开关，即从A到G，再从A始顺次拉动开关，即又从A到G…，他这样拉动了1999次开关后，问哪几盏是开的? 17．有1997枚硬币，其中1000枚国徽朝上，997枚国徽朝下．现要求每一次翻转其中任意6枚，使它们的国徽朝向相反，问能否经过有限次翻转之后，使所有硬币的国徽都朝上?给出你的结论，并给予证明．18．对一个正整数作如下操作:如果是偶数则除以2，如果是奇数则加1，如此进行直到1时操作停止，求经过9次操作变为l的数有多少个？19．高为50cm，底面周长为50cm的圆柱，在此圆柱的侧面上划分(如图所示)边长为lcm的正方形，用四个边长为lcm的小正方形构成“T”字形，用此图形是否能拼成圆柱侧面?试说明理由．参考答案。

奥数■奇数与偶数教案奥数奇数和偶数知识要点：奇数和偶数的概念：整数可以分成奇数和偶数两大类。

能被2 整除的数叫做偶数(双数)，不能被2 整除的数叫做奇数(单数) 。

特别注意，因为0 能被2 整除，所以0 是偶数。

因此最小的奇数是１，最小的偶数是0。

1、偶数与奇数的关系：偶数＋偶数= 偶数－偶数=偶数＋奇数= 偶数－奇数=奇数＋奇数= 奇数－奇数=偶数×偶数= 偶数×奇数=奇数×奇数= 偶数÷偶数=偶数÷奇数= 奇数÷奇数=2、奇数个奇数的和等于奇数，偶数个奇数的和等于偶数，任意个偶数的和等于偶数。

3、任意个奇数的积等于奇数，偶数与任意自然数之积是偶数。

4、若干个自然数的积是奇数，则每一个乘数都是奇数；若干个自然数之积是偶数，则其中必定有一个乘数是偶数。

5、相邻的两个整数必为一奇一偶，它们的积必为偶数，它们的和必为奇数。

例1、下表中有15 个数，请选出五个数，使它们的和等于30.能做到吗？为什么？例2、在2003年“非典”时期，通信公司赠送某医院27 部手机，它们的号码都是连续的。

这27 部手机的号码和是奇数还是偶数？例3 、任意改变某个三位数的各数字的次序后得到一个新的三位数 (比如423 可改变为432、342 等），试问这个新的三位数与原来的那个三位数的和能不能等于999？如果能，试举一例；如果不能，请说明理由。

例4 、赵老师在黑板上写了三个整数。

然后擦去一个数，再写上其他两个数之和；然后再随意擦去一个数，再写出其他两个数之和。

就这样一直做下去，最后得到2004,2005,2006。

赵老师一开始写的三个数有没有可能是1,3,5？例5 、张老师在黑板上依次写下0,1,3,8,21，⋯一列数，规律是：每个数的3 倍等于它前后相邻的两个数字的和，那么张老师写的第20 个数是奇数还是偶数？例6、a,b,c,d 是四个不同的质数，且a﹢b﹢c＝d,那么a×b×c×d 的积最小是多少？例7 、已知a,b,c 是三个连续的自然数，其中a 是偶数，小红和小明两人的说法正确的是（）小红：那么﹙a＋1﹚, ﹙b ＋2﹚, ﹙c＋3﹚这三个数的乘积一定是奇数。