SW6 外加强矩形截面壳体计算

不锈钢型材计算公式1.矩形、方形和圆形截面的面积计算公式：矩形截面的面积计算公式：A=b*h方形截面的面积计算公式：A=a^2圆形截面的面积计算公式：A=π*r^2其中，A代表截面的面积，b代表矩形截面的宽度，h代表矩形截面的高度，a代表方形截面的边长，r代表圆形截面的半径，π代表圆周率，约等于3.14162.不锈钢型材的截面惯性矩计算公式：截面惯性矩是评估不锈钢型材对于承载和抗弯刚度的能力的重要参数。

根据不同的截面形状和尺寸，其计算公式也会有所不同。

以下是一些常见的计算公式：矩形截面的惯性矩计算公式：I=b*h^3/12方形截面的惯性矩计算公式：I=a^4/12圆形截面的惯性矩计算公式：I=π*r^4/4其中，I代表截面的惯性矩。

3.不锈钢型材的截面模数计算公式：截面模数是评估不锈钢型材对于扭转和挤压的抵抗能力的参数。

以下是一些常见的计算公式：矩形截面的截面模数计算公式：W=b*h^2/6方形截面的截面模数计算公式：W=a^3/6圆形截面的截面模数计算公式：W=π*r^3/3其中，W代表截面的截面模数。

4.不锈钢型材的抗弯强度计算公式：抗弯强度是评估不锈钢型材对于外部力矩的抗性能力的参数。

以下是一种常见的计算公式：抗弯强度计算公式：M=σ*I/y其中，M代表外部力矩，σ代表不锈钢材料的抗弯强度，I代表截面的惯性矩，y代表截面的最大纵轴距离。

以上介绍了一些常见的不锈钢型材计算公式，希望对您的学习和工作有帮助。

需要注意的是，不同材料和结构的不锈钢型材计算公式可能会有所不同，因此在实际应用中，需要结合具体的情况和设计要求进行计算。

矿用隔爆型矩形箱体外壳强度设计计算2010-10-03 20:33:43 作者：phpcms 来源：浏览次数：330 引言矿用隔爆型外壳是电气设备的一种防爆形式，其外壳能够承受通过外壳任何接合面或结构间隙渗透到外壳内部的可燃性混合物在内部爆炸而不损坏，并且不会引起外部由一种、多种气体或蒸汽形成的爆炸性环境的点0 引言矿用隔爆型外壳是电气设备的一种防爆形式，其外壳能够承受通过外壳任何接合面或结构间隙渗透到外壳内部的可燃性混合物在内部爆炸而不损坏，并且不会引起外部由一种、多种气体或蒸汽形成的爆炸性环境的点燃。

1 矩形箱体外壳的外壁结构简化及强度计算该种结构外壳的外壁可简化为在整个板面上作用均布载荷，四边固定的等厚矩形板模型。

根据弹性力学计算，最大应力点发生在矩形长边的中心位置，即图 1中的P点。

最大挠度位置发生在板面中心位置，即0 点。

当板与板为锐角相交时，则应力将增加。

若用圆角相交时，应力集中将会降低所以在设计时尽量在板与板相交处靠圆角相交每块板的模型可以用图 1的结构简图表示板面中心的最大弯曲正应力：式中α、β——与矩形长和宽比值有关的系数( 见表 1 ) ；b——矩形板的宽度，m m；q——实验压力，MP a ；t——矩形板的厚度，m m；E——材料的弹性模量。

防爆外壳通常采用一般碳钢Q235 。

可以根据第三强度理论式中σs ——材料屈服点；n ——材料屈服极限的安全系数，一般碳钢n=1.25。

在不加加强肋的情况下，矩形外壳外壁厚度可根据式 ( 5 ) 得出在实际设计中，当边长较长，一般单边超过 3 0 0mm的矩形薄壁板在满足强度时，还要考虑壳体变形。

多采用焊接加强肋的办法来提高强度和刚度。

2 螺栓大小的计算矩形外壳的连接法兰单个螺栓轴向载荷分布不均匀，根据压力类容器计算方式，当 A ／ B>2时( 尺寸见图3 ) ，近似认为箱体内压力形成的轴向载荷由长边上的螺栓承担，单个螺栓最大载荷Q= 0 .66 B c q+ 2 d c m q ( 7 )式中 B——过螺栓中心矩形的短边长度， mm；c——螺栓中心距离， mm；d——密封垫有效宽度， m m；m——密封垫系数。

SW6计算问题汇总1. 什么叫波形膨胀节的加强圈？它起什么作用？答：指加于膨胀节直边段外侧的加强圈（一般为扁钢）。

该加强圈能减小波纹管直边段的周向薄膜应力。

2. 经常发生用水压试验压力代入后，波形膨胀节的薄膜应力较核通不过的情况。

但SW6-98未提出此要求。

答：不是SW6-98未提出此要求，而是膨胀节标准GB16749-1997未提出此要求。

3. 鞍座计算时，鞍座高度h是指鞍座的标准高度还是鞍座的腹板高度？答：由于h是用来计算鞍座腹板的平均应力s9，故应输入鞍座腹板中间处的最小高度。

4. GB151中，对筒体规定了一个最小厚度，但有时强度计算并不需这么厚，似乎有浪费，特别对于贵重有色金属设备更是如此。

答：GB151中规定的最小厚度是考虑了管束等内件重量使得在制造、安装时筒体所需要的刚度，这是必须要满足的。

但对于有色金属设备，GB151尚没有给出筒体的最小厚度，应建议标准编制单位补充该条规定。

5. 在固定管板换热器计算时，如用F19×2的管子，管子的压应力校核往往通不过，原因是计算得到的许用压应力很小，用何方法调整？答：首先，请注意管子的受压失稳当量长度是否按GB151的规定取值，该值对管子许用压应力的影响很大。

其次，管子的直径对许用压应力也有较大的影响，一般F25的管子要比F19的管子在许用压应力的计算值上大50％左右。

由于管子的直径一般不能改动，因其对换热面积有很大的影响，故工程上一般只能考虑减小折流板的间距。

当折流板的间距无法再改小时，只能由设计人员根据使用经验自行确定是否忽略换热管压应力的校核结果。

6. 计算锥形封头时，如压力很小（如p=0.1MPa），p/[s]t×f 的值往往小于0.002，这时程序不能计算，如何解决？答：由于GB150-1998中计算锥形壳体大、小端加强厚度时的Q值曲线图横座标的右端极限（p/[s]t×f）为0.002，故程序也限定此值为计算的界限。

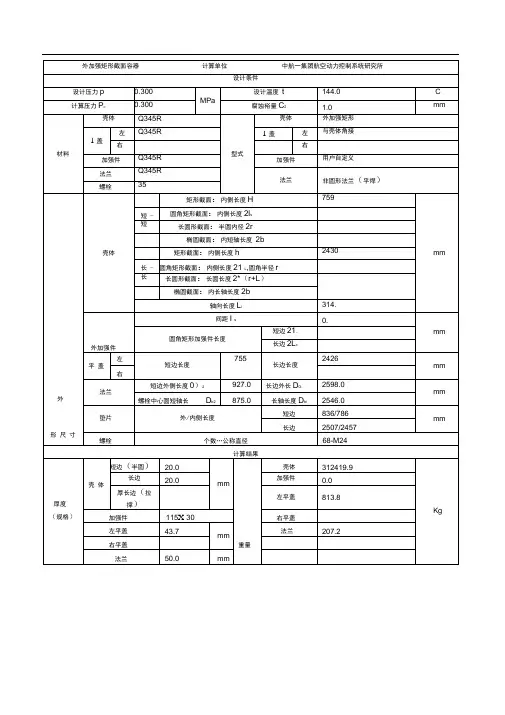
中航一集团航空动力控制系统研究所上封头计算计算单位设计条件计算压力p c 0.300 MPa设计温度t 144.0 C短轴长度a 927.0 mm平长轴长度b 2598.0 mm材料名称Q345R盖许用应力’181.0 MPa径向截面各开孔直径和0.0 mm中心圆短轴长度D b2 875.0 mm 螺中心圆长轴长度D b1 2546.0 mm 公称直径d B 24.0 mm 栓数量n 68 个材料35长轴外径长度2507.0 mm 垫短轴外径长度836.0 mm长轴内径长度2457.0 mm 短轴内径长度786.0 mm 片匕(见HG20582-2011 表12.2 -1) 120.0 k2(见HG20582-2011 表12.2 -1) 24.0i J,_a厂q1开孔削弱系数 1.00厚度设计GB150.3-2011 表5-10 序号2, 3, 4, 5, 8,结构平盖计算厚度S pGB150.3-2011 表5-10 序号9,10结构平盖计算厚度S P 结构特征系数K = 0.00形状系数Z=3.4-2.4 a= 0.000b且Z< 2.5厚度S p=a黑c= 0.0mm螺栓中心多边行周长L= 6842.0垫片受力点到螺栓中心圆间距I预紧状态时或操作状态时的螺栓设计载荷（参照HG20582-2011 计算）形状系数Z=3.4-2.4 a= 2.50bmmL G= 32.0 mmW= 966193.0 N且Z< 2.5结构特征系数K = 0.86厚度S p =a计算结果平盖有效厚度43.7 mm 校核合格37.85mm非圆形法兰（平焊）计算单位中航一集团航空动力控制系统研究所由内压引起的轴向总载荷 F 603870.62500 N 预紧状态下螺栓总载荷 W mF =966193.0 N 操作状态下螺栓总载荷 WW = m F = 966193.0N预紧状态下所需螺栓总截面积An AWm8258.1AA m[]b2mm 操作状态下所需螺栓总截面积 A pWpA P 十 9775.3[]b2mm 所需螺栓总截面积 A A 取 A m 和A p 中大者 A = 9775.32mm 实际螺栓总截面积AA b = n —dB 2= 21362.842mm设计条件-简所 口 右~i ：• ° 口 咼预紧状态下 M W1732821.0 N S w =32.0 mm M =WS = 55450272.0 Nmm操作状态下 MF D =553311.0 N S D =16.0 mm M = F D S +F T S T +WS W=40428428.0Nmm F T = 50559.6NS T = 13.0 mm计算力矩 M 取M 与【中大者 M = 53293536.0/ [J fNmmN S w =0.0 mm 计算力矩 M =0.5 F D S W 或 M =F D S W M = 0.0Nmm垫片位于螺栓内侧的法兰2.全垫片法兰F D =0.0。

3D建模，用SW画一个带加强筋的壳体，筋的位置是个容易
出错的地方
渲染图一
渲染图二
渲染图三
图纸
详细建模步骤：
1.在上视基准面画一个正方形，边长：80 。

然后拉伸凸台：10 。

2.在立方体顶面草绘图形。

3.拉伸切除，高度：6 。

4.在切除后的面上画圆，拉伸切除：4 。

5.在正立方体顶面画圆，拉伸高度：6 。

6.圆周阵列——两个拉伸切除——数量4个。

7.倒角：3*45度。

8.在立方体顶面草绘图形。

（这条中心线后面还要用来建基准面）
9.拉伸凸台，高度：4 ，不合并结果。

（这两步应该是：画一条斜线，然后用筋特征来完成。

后来发现，外侧边线长度不是20，所以改用这个方法）
10.新建基准面，参考上视基准面和中心线。

11.在新建基准面上画三角形。

12.拉伸切除，特征范围：只选两个立方体。

13.圆周阵列——实体。

14.组合。

15.抽壳，点底面，厚度：1 。

16.上视基准面上画圆。

17.拉伸切除。

18.还是上视基准面，等距实体。

延伸和剪裁
20.拉伸切除，完全贯穿。

21.圆周阵列4个。

22.测量体积，选项——精度高——8473.79，正确。

23.完成。

截面面积矩sw计算公式
截面面积矩是一个非常重要的物理量，它在工程学、物理学、材料科学等领域中都有着广泛的应用。

截面面积矩的计算公式是一个基本的数学公式，它可以用来计算各种形状的截面的面积矩，从而帮助我们更好地理解和分析物体的结构和性质。

截面面积矩的计算公式可以表示为：
S_w = ∫ y^2 dA
其中，S_w表示截面面积矩，y表示距离截面中心轴的距离，dA 表示微小面积元素。

这个公式的意义是将整个截面分成无数个微小的面积元素，然后对每个微小的面积元素进行计算，最后将所有的计算结果相加得到截面面积矩。

截面面积矩的计算公式可以用来计算各种形状的截面的面积矩，例如矩形、圆形、三角形、梯形等等。

对于不同形状的截面，我们需要根据其特点来选择不同的计算方法。

例如，对于矩形截面，我们可以直接使用公式S_w = bh^3/12来计算其面积矩；对于圆形截面，我们可以使用公式S_w = πr^4/4来计算其面积矩。

截面面积矩的计算公式在工程学中有着广泛的应用。

例如，在设计梁或柱子时，我们需要计算其截面面积矩，以确定其承载能力和稳定性。

在设计机械零件时，我们也需要计算其截面面积矩，以确定其强度和刚度。

在材料科学中，截面面积矩的计算公式也可以用来
计算材料的惯性矩和截面模量等重要参数。

截面面积矩的计算公式是一个非常重要的数学公式，它在工程学、物理学、材料科学等领域中都有着广泛的应用。

通过掌握这个公式，我们可以更好地理解和分析物体的结构和性质，从而为工程设计和科学研究提供有力的支持。

截面面积范围计算公式在工程设计和科学研究中，计算截面面积范围是一项非常重要的工作。

截面面积是指在某一平面上，所围成的图形的面积。

在不同的领域中，截面面积的计算公式也各不相同。

本文将介绍一些常见的截面面积计算公式，并举例说明其应用。

一、矩形截面面积计算公式。

矩形是一种常见的截面形状，其截面面积计算公式为：A = b h。

其中，A表示截面面积，b表示矩形的宽度，h表示矩形的高度。

例如，一个宽度为2米，高度为3米的矩形的截面面积为6平方米。

二、圆形截面面积计算公式。

圆形是另一种常见的截面形状，其截面面积计算公式为：A = π r^2。

其中，A表示截面面积，π表示圆周率，r表示圆的半径。

例如，一个半径为4米的圆的截面面积为16π平方米。

三、三角形截面面积计算公式。

三角形是一种常见的截面形状，其截面面积计算公式为：A = 0.5 b h。

其中，A表示截面面积，b表示三角形的底边长度，h表示三角形的高度。

例如，一个底边长度为5米，高度为6米的三角形的截面面积为15平方米。

四、梯形截面面积计算公式。

梯形是一种常见的截面形状，其截面面积计算公式为：A = 0.5 (a + b) h。

其中，A表示截面面积，a和b分别表示梯形的上底和下底长度，h表示梯形的高度。

例如，一个上底长度为3米，下底长度为5米，高度为4米的梯形的截面面积为16平方米。

五、复杂形状截面面积计算公式。

对于一些复杂的截面形状，可以通过将其分解成简单的几何形状，然后分别计算其截面面积，最后将各个部分的截面面积相加得到整体的截面面积。

这种方法可以适用于任意形状的截面。

在工程设计中，截面面积的计算常常涉及到不同形状的材料，比如钢材、混凝土等。

根据不同材料的特性和使用要求，需要选择合适的截面形状和尺寸。

通过计算截面面积范围，可以帮助工程师和设计师更好地选择合适的材料和尺寸，从而确保工程的安全和稳定。

总结起来，截面面积计算是工程设计和科学研究中的重要内容，不同形状的截面有不同的计算公式，通过计算截面面积可以帮助选择合适的材料和尺寸，确保工程的安全和稳定。

常用截面几何特性计算公式截面几何特性是指用于描述一个截面的形状和大小的参数，常用的包括面积、惯性矩、截面模量、截面半径等。

这些参数在工程中非常重要，因为它们能够直接影响截面的受力性能。

下面将介绍一些常用的截面几何特性计算公式。

1.截面面积计算公式：截面面积是指截面内部所有点的面积总和。

对于一些常见的截面形状，可以使用以下公式进行计算：-矩形截面面积：A=b*h，其中b为矩形的宽度，h为矩形的高度。

-圆形截面面积：A=π*r^2，其中r为圆的半径。

-等边三角形截面面积：A=(s^2*√3)/4，其中s为三角形的边长。

-梯形截面面积：A=(a+b)*h/2，其中a和b为梯形的上底和下底长度，h为梯形的高度。

2.截面惯性矩计算公式：惯性矩是描述截面抵御扭转和弯曲的能力的参数。

对于一些常见的截面形状，可以使用以下公式进行计算：-矩形截面惯性矩：I=(b*h^3)/12，其中b为矩形的宽度，h为矩形的高度。

-圆形截面惯性矩：I=π*r^4/4，其中r为圆的半径。

-等边三角形截面惯性矩：I=(s^4*√3)/64，其中s为三角形的边长。

-梯形截面惯性矩：I=[(b1*h1^3)+(b2*h2^3)]/12，其中b1和b2为梯形的上底和下底长度，h1和h2为梯形的高度。

3.截面模量计算公式：截面模量是描述截面抵御弯曲的能力的参数。

对于一些常见的截面形状，可以使用以下公式进行计算：-矩形截面模量：S=(b*h^2)/6，其中b为矩形的宽度，h为矩形的高度。

-圆形截面模量：S=π*r^3/3，其中r为圆的半径。

-等边三角形截面模量：S=(s^3*√3)/36，其中s为三角形的边长。

-梯形截面模量：S=[(b1*h1^2)+(b2*h2^2)]/6，其中b1和b2为梯形的上底和下底长度，h1和h2为梯形的高度。

4.截面半径计算公式：截面半径是描述截面的曲率半径的参数，通常用于弯曲性能的评估。

-矩形截面半径：r=h/2，其中h为矩形的高度。

不锈钢型材计算公式一、截面积计算公式：截面积是不锈钢型材的重要参数，用来衡量型材所能承受的载荷和抵抗变形的能力。

不锈钢型材的截面积计算可以根据形状的不同采用不同的公式，以下是一些常见形状的计算公式：1.矩形截面（宽b，高h）的截面积A：A=b×h2.圆形截面（半径r）的截面积A：A=π×r²3.圆管截面（外径d，内径d1）的截面积A：A=π×(d²-d1²)/44.L型截面（长边b，短边h）的截面积A：A=b×h5.T型截面（长边b，腰边h）的截面积A：A=b×h二、惯性矩和截面模量计算公式：惯性矩和截面模量是描述不锈钢型材抵抗弯曲和变形能力的重要参数。

它们的计算可以通过截面积和截面形状的几何参数来确定：1. 矩形截面的惯性矩I和截面模量W：I = bh³ / 12，W = bh² / 62.圆形截面的惯性矩I和截面模量W：I=πr⁴/4，W=πr³/43.圆管截面的惯性矩I和截面模量W：I=(π/4)×(d²-d1²)²，W=(π/4)×(d²-d1²)4. L型截面的惯性矩I和截面模量W：I = (bh³ - (b1h1³)) / 12，W = (bh² - b1h1²) / 65. T型截面的惯性矩I和截面模量W：I = (bh³ - (b1h1³)) / 12，W = (bh² - b1h1²) / 6三、抗弯强度计算公式：抗弯强度M=σ×W其中，σ为材料的抗弯应力，可以通过材料的抗弯强度和安全系数来确定。

四、屈服强度计算公式：屈服强度F=σ×A其中，σ为不锈钢的屈服应力。

以上是关于不锈钢型材计算的一些基本公式和方法，通过这些公式可以对不锈钢型材的尺寸和力学性能进行合理的估计和设计。

截面与体积的计算方法总结截面和体积的计算是在数学和物理学中经常遇到的问题。

正确地计算截面和体积对于解决各种应用问题至关重要。

本文将总结截面和体积计算的一些常见方法，并提供详细的计算步骤和示例。

一、平面几何中的截面计算方法1.1 矩形截面的计算方法矩形截面是最简单的一种截面形状。

要计算矩形截面的面积，只需要知道矩形的长度和宽度，然后将两者相乘即可。

例如，假设一个矩形的长度为4cm，宽度为3cm，则该矩形的面积为4cm * 3cm = 12cm²。

1.2 圆形截面的计算方法圆形截面在工程学和自然科学中经常出现。

要计算圆形截面的面积，需要知道圆的半径。

圆的面积计算公式为：面积= π * 半径²，其中π约等于3.14159。

例如，假设一个圆形的半径为5cm，则该圆形的面积为3.14159 *5cm * 5cm = 78.53975cm²。

二、立体几何中的体积计算方法2.1 立方体的计算方法立方体是最简单的一种立体形状。

要计算立方体的体积，只需要知道立方体的边长，然后将边长立方即可。

例如，假设一个立方体的边长为5cm，则该立方体的体积为5cm * 5cm * 5cm = 125cm³。

2.2 圆柱体的计算方法圆柱体常见于工程学和日常生活中。

要计算圆柱体的体积，需要知道圆的半径和圆柱体的高。

圆柱体的体积计算公式为：体积= π * 半径² * 高。

例如，假设一个圆柱体的半径为3cm，高为8cm，则该圆柱体的体积为3.14159 * 3cm * 3cm * 8cm = 226.19528cm³。

2.3 球体的计算方法球体是三维空间中的一种完全圆形。

要计算球体的体积，需要知道球的半径。

球体的体积计算公式为：体积= (4/3) * π * 半径³。

例如，假设一个球体的半径为6cm，则该球体的体积为(4/3) *3.14159 * 6cm * 6cm * 6cm = 904.77868cm³。

截面面积矩sw计算公式截面面积矩SW计算公式是一种常用的工程计算公式，它通常用来计算截面受力时的矩阵，包括一阶截面面积矩和二阶截面面积矩。

这些矩阵对于设计工程结构时非常重要，因为它们可以帮助工程师预测结构的性能和响应。

在本文中，我们将介绍截面面积矩SW计算公式的原理、用途及其详细运用。

我们还将提供一些实际工程案例，以帮助读者更好地理解截面面积矩的概念和计算方法。

一、原理截面面积矩SW计算公式基于两个基本原理。

第一个原理是面积定积分，这是一个基本的数学原理，用于计算曲线下面积。

这个原理对于计算截面面积矩非常重要，因为我们可以将截面分为无数小的面积元素，然后通过积分来计算面积。

第二个原理是微积分，它是一个基本的数学原理用于计算函数的导数和积分。

通过这个原理，我们可以计算截面的任意一阶和二阶矩阵。

二、用途截面面积矩SW计算公式广泛应用于各种工程领域，如建筑、机械、水利等。

它可以用于设计弯曲构件、挑战地梁、梁柱节点等结构的截面形状和大小。

通过计算截面面积矩，我们可以确定截面的惯性矩和截面模量，从而预测结构的刚度、挠度和强度等性能。

三、详细运用截面面积矩SW计算公式的运用需要从一元、二元、三元三维空间等不同角度来思考。

下面我们将针对这些不同角度来分别介绍其详细运用方法。

1. 一元计算一元计算是最基本的截面面积矩SW计算方法，它仅考虑结构的平面形状，通常用于计算梁的截面形状和大小。

以下是一元计算的具体步骤：（1）将梁截面划分为一系列小面积元素；（2）计算每个小面积元素的面积、重心和距离；（3）计算一阶截面面积矩和二阶截面面积矩；（4）计算截面的惯性矩和截面模量；（5）根据计算结果确定梁的截面形状和大小。

2. 二元计算二元计算是比一元计算更高级的截面面积矩SW计算方法，它考虑结构的平面形状和立面形状，通常用于计算柱子的截面形状和大小。

以下是二元计算的具体步骤：（1）将柱子截面划分为一系列小面积元素；（2）计算每个小面积元素的面积、重心和距离；（3）计算一阶截面面积矩和二阶截面面积矩；（4）计算柱子的惯性矩和截面模量；（5）根据计算结果确定柱子的截面形状和大小。

中航一集团航空动力控制系统研究所上封头计算计算单位设计条件计算压力p c 0.300 MPa设计温度t 144.0 C短轴长度a 927.0 mm平长轴长度b 2598.0 mm材料名称Q345R盖许用应力’181.0 MPa径向截面各开孔直径和0.0 mm中心圆短轴长度D b2 875.0 mm 螺中心圆长轴长度D b1 2546.0 mm 公称直径d B 24.0 mm 栓数量n 68 个材料35长轴外径长度2507.0 mm 垫短轴外径长度836.0 mm长轴内径长度2457.0 mm 短轴内径长度786.0 mm 片匕(见HG20582-2011 表12.2 -1) 120.0 k2(见HG20582-2011 表12.2 -1) 24.0i J,_a厂q1开孔削弱系数 1.00厚度设计GB150.3-2011 表5-10 序号2, 3, 4, 5, 8,结构平盖计算厚度S pGB150.3-2011 表5-10 序号9,10结构平盖计算厚度S P 结构特征系数K = 0.00形状系数Z=3.4-2.4 a= 0.000b且Z< 2.5厚度S p=a黑c= 0.0mm螺栓中心多边行周长L= 6842.0垫片受力点到螺栓中心圆间距I预紧状态时或操作状态时的螺栓设计载荷（参照HG20582-2011 计算）形状系数Z=3.4-2.4 a= 2.50bmmL G= 32.0 mmW= 966193.0 N且Z< 2.5结构特征系数K = 0.86厚度S p =a计算结果平盖有效厚度43.7 mm 校核合格37.85mm非圆形法兰（平焊）计算单位中航一集团航空动力控制系统研究所由内压引起的轴向总载荷 F 603870.62500 N 预紧状态下螺栓总载荷 W mF =966193.0 N 操作状态下螺栓总载荷 WW = m F = 966193.0N预紧状态下所需螺栓总截面积An AWm8258.1AA m[]b2mm 操作状态下所需螺栓总截面积 A pWpA P 十 9775.3[]b2mm 所需螺栓总截面积 A A 取 A m 和A p 中大者 A = 9775.32mm 实际螺栓总截面积AA b = n —dB 2= 21362.842mm设计条件-简所 口 右~i ：• ° 口 咼预紧状态下 M W1732821.0 N S w =32.0 mm M =WS = 55450272.0 Nmm操作状态下 MF D =553311.0 N S D =16.0 mm M = F D S +F T S T +WS W=40428428.0Nmm F T = 50559.6NS T = 13.0 mm计算力矩 M 取M 与【中大者 M = 53293536.0/ [J fNmmN S w =0.0 mm 计算力矩 M =0.5 F D S W 或 M =F D S W M = 0.0Nmm垫片位于螺栓内侧的法兰2.全垫片法兰F D =0.0。

壳体计算公式好的，以下是为您生成的文章：在咱们的日常生活和学习中，各种形状的壳体那可是无处不在。

就拿咱们常见的鸡蛋壳来说，它看起来普普通通，但其实蕴含着不少有趣的数学知识呢！今天咱们就来聊聊壳体计算公式。

说起壳体，大家可能会觉得有点陌生，但要是提到篮球、乒乓球、易拉罐，是不是一下子就觉得熟悉多啦？这些东西的形状都可以看作是壳体的一种。

那什么是壳体呢？简单来说，壳体就是由曲面构成的薄壁结构。

比如像灯泡的玻璃罩、汽车的油箱，它们的外表都是壳体。

接下来咱们就讲讲壳体的计算公式。

在这之前，咱们先得搞清楚一些基本的概念。

比如说，壳体的中面，这可是计算中非常重要的一个部分。

中面就是壳体厚度的中间那一层。

对于常见的旋转壳体，像球形壳体、圆柱形壳体，它们都有各自的计算公式。

就拿球形壳体来说吧，假如这个球的半径是 R ，那么它的表面积公式就是4πR² 。

想象一下，一个足球，咱们要计算它外表皮的面积，用这个公式就能轻松搞定。

再说说圆柱形壳体，如果圆柱的底面半径是 r ，高是 h ，那它的侧面积就是2πrh 。

这就好比一个易拉罐，咱们要知道它侧面那一圈的面积，用这个公式就能算出来。

我记得有一次，我带着学生们去工厂参观。

看到了好多正在加工的壳体零件。

当时有个学生就好奇地问工人师傅：“师傅，您怎么能这么准确地算出这些壳体的各种数据呢？”工人师傅笑着说：“那可多亏了这些计算公式啊，它们就像是我们的秘密武器，能让我们又快又准地完成工作。

”在学习壳体计算公式的时候，可不能死记硬背，得理解着来。

多做几道练习题，结合实际的物体去思考，这样才能真正掌握。

比如说，咱们可以自己动手做一个简单的纸质圆柱形壳体，然后通过测量和计算，来验证公式的正确性。

总之，壳体计算公式虽然看起来有点复杂，但只要咱们用心去学，多观察、多思考、多实践，就一定能把它拿下。

就像咱们解决生活中的其他难题一样，只要有耐心、有方法，就没有什么能难倒咱们的！希望大家通过对壳体计算公式的学习，能发现更多数学在生活中的奇妙应用，让数学成为咱们的好帮手，而不是头疼的难题。

一、基
柱截面宽b 柱截面高h 柱高L 原构件混凝土
强度等级
柱中纵向钢筋面积A s0'
500
500
5000
23.5
3140棱角的圆化半径r 纤维复合材的层数n f 纤维复合材每层厚度t f 加固构件的构件类别碳纤维布种类30
3
0.167
一般构件
高强度II级单向织物柱中纵向钢筋的配筋
率ρs
1.26%
加固前柱轴
压比U 0轴压比限制[U]
0.818
0.8
二、加
249227.40.4760.0040.6880.696
U加固≤[U],加固后柱轴压比满足要求
柱轴压比不满足要求，需要加固
可以采用环向围束法进行加固
设计依据：《混凝土结构加固设计规范》GB50367-2013中第10.4章1. 环向围束内混凝土面积A cor =bh－(4－π)r 2 (mm 2)2.环向围束的有效约束系数
3.环向围束体积比ρf ＝2n f t f (b＋h)/A cor
4.有效约束应力 (N/mm 2)
5.加固后柱轴压比U 加固=F/[bh*(f c0+4σl )]
200000
0.0045
加固前柱轴力设计值F （N）
3215000
柱是否满足长细比l/d≤14、截面高宽比h/b≤1.5、
截面高度h≤600mm
满足
矩形柱环向围束法加固
轴心抗压强度设计值f c0
混凝土强度影响系数βc
15.7
0.8
纤维复合材的弹性模量Ef
纤维复合材的有效拉应变设
计值εfe。

矩形梁截面强度计算书项目名称_____________构件编号_____________日期_____________ 设 计_____________校 对_____________审核_____________二、计算结果1．主筋1．1 相对界限受压区高度 ξbεcu = 0.0033 - (f cu,k - 50)×10-5 = 0.0033 - (30 - 50)×10-5 = 0.0035 > 0.0033取 εcu = 0.0033按规范公式(7.1.4-1)ξb = β11 + f y E s εcu = 0.801 + 3602.0×105×0.0033 = 0.521．2 受压区高度x按规范公式(7.2.1-1), A 's = 0, A 'p = 0 M = α1f c bx ⎝⎛⎭⎫h 0 - x 2x = h 0 - h 02 - 2M α1f c b = 565 - 5652 - 2×265.61×1061.00×14.30×300 = 123mm< ξb h 0 = 0.52×565 = 292.47mm, 按计算不需要配置受压钢筋1．3 受拉钢筋截面积A s按规范公式(7.2.1-2)α1f c bx = f y A s得 A s = α1f c bx f y = 1.00×14.30×300×123360 = 1465mm 21．4 验算配筋率验算最大配筋率时取ρ = A s bh 0 = 1465300×565×100% = 0.86%< ρmax = 2.50% 不超筋验算最小配筋率时取ρ = A s bh = 1465300×600×100% = 0.81%根据混凝土结构设计规范(GB50010-2002)表11.3.6-1⎭⎬⎫ρmin = 0.250%ρmin = 0.55f t /f y = 0.55×1.43/360 = 0.218%ρmin = 0.250% < ρ满足最小配筋率要求实配受拉钢筋(梁底): 5C 20, A s = 1571mm 2规范第11.3.7条,受压钢筋不能小于受拉钢筋面积的0.25倍，取A 's = 0.25×A s = 366mm 2实配受压钢筋(梁顶): 4C 12, A 's = 452mm 22．箍筋2．1 复核截面条件按规范公式(11.3.3)0.20βc f c bh 0 = 0.20×1.00×14.30×300×565 = 484.8×103NV = 142.4kN < 0.20×1.00×14.30×300×565 = 484.8kN, 截面尺寸满足要求2．2 验算构造配筋条件按规范公式(11.3.4-1)0.42f t bh 0 = 0.42×1.43×300×565 = 101.8×103N < V = 142.4kN应按计算配置箍筋2．3 求箍筋截面面积及间距按规范公式(11.3.4-1) V = 0.42f t bh 0 + 1.25f yv A sv s h 0即 142400 = 0.42×1.43×300×565 + 1.25×210.0×A sv s ×565 得 A sv s = 0.2737 mm 2/mm 根据混凝土规范第11.3.9条 V = 142.4kN > 0.42f t bh 0 = 101.8N 0.28bf t /f yv = 0.5720 mm 2/mm > A sv s = 0.2737 mm 2/mm 取 A sv s = 0.5720 mm 2/mm 根据计算配置四肢箍筋 A 8@90⎝⎛⎭⎫A sv s = 4×50.390 = 2.2340 mm 2/mm。