1圆面积和周长的对比(20201015165016)

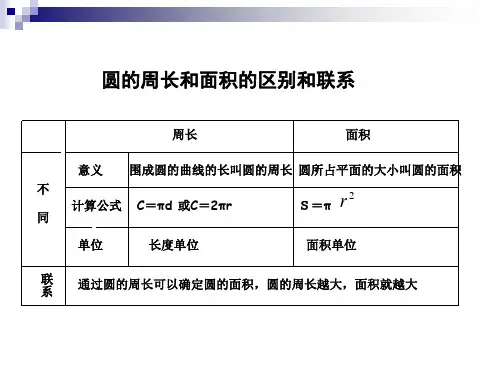
圆的面积和周长的关系可以通过公式表示。

具体来说，周长和直径之间有关系，用公式表示为C=πd或者C=2πr，其中C表示周长，d表示直径，r表示半径，π是圆周率，取值约为3.1415927。

同时，圆的面积和半径之间有关系，用公式表示为S=πr²或者S=π(d/2)²，其中S表示面积，r表示半径，d表示直径，π是圆周率。

通过观察公式可以发现，当直径或半径增大时，圆的周长也会随之增大，而面积则会增大得更快。

这是因为面积和半径的平方成正比，而周长和半径或直径成正比。

因此，当半径或直径增大时，面积的增长速度要比周长的增长速度更快。

总结来说，圆的面积和周长之间存在一定的关系，它们都与半径或直径有关。

公式可以用来表示这种关系。

圆的周长和面积学会计算圆的周长和面积圆是不规则几何图形中的一种，它具有许多特殊的性质，如圆的周长和面积。

本文将介绍如何计算圆的周长和面积，以帮助读者更好地理解和应用这两个重要的概念。

一、圆的周长计算方法圆的周长即圆周上所有点到圆心的距离之和。

为了计算圆的周长，我们需要知道圆的半径或直径。

1.1 圆的半径计算方法圆的半径是从圆心到圆周上任意一点所连接的线段的长度。

圆的半径通常用字母r表示。

如果我们已知圆的直径d，可以通过以下公式计算圆的半径：r = d/21.2 圆的周长计算公式当我们知道圆的半径r时，可以使用以下公式计算圆的周长C：C = 2πr其中，π（pi）是一个常数，约等于3.14159。

将半径代入公式，我们就可以得到圆的周长。

二、圆的面积计算方法圆的面积是指圆内部所有点所围成的部分的大小。

同样，为了计算圆的面积，我们需要知道圆的半径或直径。

2.1 圆的面积计算公式当我们知道圆的半径r时，可以使用以下公式计算圆的面积A：A = πr^2这个公式表示圆的面积等于半径的平方乘以π。

通过将半径代入公式，我们就可以计算圆的面积。

2.2 圆的面积与周长的关系可以发现，圆的面积和周长之间存在着一定的关系。

以半径为定值，当半径增加时，圆的周长和面积都会增加；当半径减小时，圆的周长和面积都会减小。

这说明了半径对于圆的周长和面积具有重要影响。

三、例题解析为了更好地理解和应用圆的周长和面积的计算方法，我们来看一个例题。

假设一个圆的半径为5cm，我们需要计算该圆的周长和面积。

首先，根据周长计算公式C = 2πr，代入已知的半径r = 5cm，可以得到周长的计算结果：C = 2π × 5 = 10π ≈ 31.42cm使用面积计算公式A = πr^2，代入已知的半径r = 5cm，可以得到面积的计算结果：A = π × 5^2 = 25π ≈ 78.54cm²因此，该圆的周长约为31.42cm，面积约为78.54cm²。

面积与周长的比较引言在几何学中，面积和周长是两个常用的度量。

面积表示一个二维形状所占据的空间大小，而周长则表示一个形状的边界长度。

在不同的几何形状中，面积与周长之间的关系可以各不相同。

本文将探讨面积与周长的比较，以及它们在不同形状中的关系。

矩形矩形是一种常见的几何形状，具有四条相互平行的边和四个角的特征。

一个矩形的面积可以通过将其长度和宽度相乘来计算。

而周长则可以通过将长度和宽度乘以2并相加来计算。

面积和周长的公式如下：面积 = 长度 × 宽度周长 = 2 × (长度 + 宽度)可以观察到，在固定长度下，增加宽度会增加矩形的面积和周长，而在固定宽度下，增加长度也会增加矩形的面积和周长。

因此，可以得出结论：面积和周长在矩形中是正相关的。

正方形正方形是一种特殊的矩形，具有四条相等的边和四个直角的特征。

由于正方形的边长相等，它的面积和周长的计算公式非常简单。

正方形的面积可以通过将边长平方来计算，周长可以通过将边长乘以4来计算。

面积和周长的公式如下：面积 = 边长 × 边长周长 = 4 × 边长可以观察到，在正方形中，当边长增加时，面积和周长都会以相同的比例增加。

因此，可以得出结论：面积和周长在正方形中也是正相关的。

圆圆是一个平面上到一个固定点距离相等的所有点的集合。

圆的面积可以通过将圆周率π乘以半径的平方来计算，周长则可以通过将圆周率π乘以直径来计算。

面积和周长的公式如下：面积= π × 半径²周长= π × 直径在圆中，半径和直径是相互关联的。

半径是一个圆周上的任意点到圆心的距离，而直径则是通过圆心的任意两点之间的距离的两倍。

由于半径和直径的关系是固定的，所以在圆中，面积和周长也是固定比例的。

结论综上所述，面积和周长在不同的几何形状中有不同的关系。

在矩形和正方形中，面积和周长是正相关的，即当一个增加时，另一个也会增加。

而在圆中，面积和周长是固定比例的，即面积和周长之间存在一个固定的关系。

圆的面积公式与周长公式圆是数学中一种重要的几何形体，其特点是每个点到圆心的距离都相等。

在日常生活中，我们经常会遇到各种圆形的物体，如轮胎、蛋糕、铅笔顶等，因此学习圆的面积公式和周长公式是非常重要的。

本文将为大家介绍圆的面积公式和周长公式。

首先，我们来介绍圆的面积公式。

圆的面积公式是指圆形的面积与半径的关系，用符号表示为S=πr²，其中S表示圆的面积，π是一个特殊的数字，称为圆周率，约等于3.14，r表示圆的半径。

根据圆的面积公式可以算出不同半径的圆的面积，例如，当半径为1时，圆的面积为3.14平方单位，当半径为2时，圆的面积为12.56平方单位。

其次，我们来介绍圆的周长公式。

圆的周长公式是指圆形的周长与半径的关系，用符号表示为C=2πr，其中C表示圆的周长，π是圆周率，r表示圆的半径。

根据圆的周长公式可以算出不同半径的圆的周长，例如，当半径为1时，圆的周长为6.28单位长度，当半径为2时，圆的周长为12.56单位长度。

需要注意的是，圆的周长和直径的关系为C=πd，其中d表示圆的直径。

对于学习与应用圆的面积与周长公式，有以下几点指导意义：首先，需熟记圆的面积与周长公式，以及圆周率的数值。

这是进行计算的基础。

其次，需要懂得如何应用圆的面积与周长公式解决实际问题。

例如，可以用圆的面积公式计算铁盘的表面积，用圆的周长公式计算车轮的周长，用直径和周长的关系解决各种问题。

最后，需要给出准确的答案，并正确使用单位。

在应用圆的面积与周长公式进行计算时，需要注意单位的问题，如面积的单位是平方单位，周长的单位是长度单位。

综上所述，圆的面积与周长是解决许多实际问题时不可或缺的数学工具，应正确学习和应用，才能更好地服务于我们的生活。

面积和周长的对比引言面积和周长是数学中常见的概念，在几何学和物理学等领域中起着重要的作用。

面积和周长既有相似之处，又有着独特的特点。

本文将探讨面积和周长的定义、计算方法和其在实际生活中的应用。

面积的定义和计算面积是一个平面图形所占据的空间大小的度量，常用单位有平方厘米、平方米等。

不同的图形有不同的计算方法。

矩形的面积计算公式矩形是最简单的图形之一，其面积计算公式为：面积 = 长 × 宽。

例如，一块长为10米，宽为5米的矩形的面积为 10 × 5 = 50 平方米。

圆的面积计算公式圆是一个没有边界的闭合曲线，其面积计算公式为：面积= π × 半径的平方。

其中，π（pi）是一个特殊的数，近似值为3.14159。

例如，一个半径为5厘米的圆的面积为 3.14159 × 5² = 78.54 平方厘米。

三角形的面积计算公式三角形是由三条边所围成的图形，其面积计算公式为：面积 = 底边长度 × 高 ÷ 2。

例如，一个底边长为6厘米，高为4厘米的三角形的面积为 6 × 4 ÷ 2 = 12 平方厘米。

周长的定义和计算周长是一个闭合曲线的长度，常用单位有厘米、米等。

同样，不同的图形有不同的计算方法。

矩形的周长计算公式矩形的周长计算公式为：周长 = 2 × (长 + 宽)。

例如，一个长为10米，宽为5米的矩形的周长为 2 × (10 + 5) = 30 米。

圆的周长计算公式圆的周长计算公式为：周长= 2 × π × 半径。

例如，一个半径为5厘米的圆的周长为 2 × 3.14159 × 5 = 31.42 厘米。

三角形的周长计算公式三角形的周长计算公式为：周长 = 边1 + 边2 + 边3。

例如，一个边1长为5厘米，边2长为6厘米，边3长为7厘米的三角形的周长为 5 + 6 + 7 = 18 厘米。

面积和周长的对比引言面积和周长是我们在日常生活和工作中经常用到的两个数学概念，它们通常被用来描述不同形状的图形。

面积是指一个平面图形所占据的空间大小，通常用平方单位来表示。

周长则是指图形边界上的长度，通常用长度单位来表示。

这两个概念在几何学中是非常重要的，因为它们可以帮助我们计算和比较不同形状的图形。

在本文中，我们将探讨面积和周长的不同特点，并分析它们在实际应用中的作用。

形状的不同不同的图形具有不同的形状，因此它们的面积和周长也会有所差别。

以下是一些常见图形的面积和周长计算公式：•正方形：面积=边长的平方，周长=4 * 边长•长方形：面积=长 * 宽，周长=2 * （长 + 宽）•圆形：面积=π * 半径的平方，周长=2 * π * 半径•三角形：面积=底边长度 * 高 / 2，周长=各边长度之和可以发现，不同图形的面积和周长计算公式的差异主要在于它们的形状。

例如，正方形和长方形都是矩形，其面积公式相同，但周长公式有所不同。

面积和周长的应用在实际应用中，面积和周长都有着广泛的应用。

以下是一些常见的案例：1. 建筑领域在建筑领域，面积和周长被用来计算建筑物的大小和形状。

例如，在设计一栋房屋时，需要计算房间的面积和周长，以确定需要多少材料。

同样，在设计一座大楼时，需要计算地面的面积和周长，以确定需要多少钢筋混凝土。

2. 地理信息系统在地理信息系统（GIS）中，面积和周长被用来计算地形和地貌的大小和形状。

例如，在计算一块土地的总面积时，可以使用面积公式。

同样，在计算一条河流的长度时，可以使用周长公式。

3. 科学计算在科学计算中，面积和周长被用来计算各种物理量。

例如，在计算圆形的体积时，需要计算其面积，并使用面积公式和高度计算。

同样，在计算三角形的重心时，需要计算其面积，并使用周长公式计算各条线段的距离。

面积和周长的对比虽然面积和周长都是描述不同形状的图形的重要概念，但它们的应用不同。

下面是一些面积和周长的比较：1. 相对大小面积通常比周长更重要，因为它可以用来计算所需的材料和资源。

圆的面积与周长圆是一种具有特殊几何属性的平面图形，它呈现出完美的对称性。

圆的面积和周长是研究圆的重要性质，本文将从不同的角度探讨这两个概念的关系。

一、圆的定义及基本属性在几何学中，圆是由一个固定点到平面上所有距离等于半径长度的点构成的。

圆的基本属性包括半径、直径、弧长和圆心角等，并且这些属性之间存在着一定的关系。

1. 圆的半径和直径圆的半径是从圆心到任一点的距离，通常用字母r表示。

直径是通过圆心的两个点之间的距离，用字母d表示。

根据定义，直径等于半径的两倍，即d = 2r。

2. 圆的周长圆的周长是指圆形边界的长度。

根据定义，圆的周长等于直径乘以π(pi)，即C = πd。

或者可以用半径表示，即C = 2πr。

3. 圆的面积圆的面积是指圆所占据的平面的大小。

根据定义，圆的面积等于半径平方乘以π，即A = πr²。

面积也可以用直径表示，即A = (π/4)d²。

二、圆的面积和周长的计算公式1. 面积计算公式根据上述定义，圆的面积计算公式是A = πr²。

这个公式表明，圆的面积与半径的平方成正比，与圆周率π成正比。

通过这个公式，我们可以计算出任意半径的圆的面积。

2. 周长计算公式根据上述定义，圆的周长计算公式是C = 2πr。

这个公式表明，圆的周长与半径成正比，与圆周率π成正比。

通过这个公式，我们可以计算出任意半径的圆的周长。

三、面积与周长的关系1. 面积和周长的比较面积和周长是圆的两个重要属性，它们之间存在着一定的关系。

从定义上来看，面积是单位长度的平面所占据的大小，而周长是单位长度的边界线的长度。

所以可以得出结论：对于相同半径的圆而言，面积比周长更能体现圆的大小。

2. 面积和周长的数值关系根据上述公式，我们可以进一步探讨面积和周长的数值关系。

在相同半径的情况下，当半径增加时，圆的面积和周长都会增大，但是面积增加的比例大于周长。

这是因为面积与半径的平方成正比，而周长与半径成正比。

圆的面积和周长的关系圆是一种基本的几何形体，其面积和周长是圆最基本的属性之一。

在学习圆的时候，我们需要重点学习和理解圆的面积和周长的关系。

本文将分步骤讲解圆的面积和周长的关系，以帮助大家更深刻地理解圆周率和圆的基本性质。

首先，我们需要了解圆的基本概念。

圆是一种闭合的曲线，其上的任意一点到圆心的距离都相同。

圆心是圆上所有点到中心的距离相等的点。

半径则是圆心到圆上任意一点的距离。

直径是圆上任意两点间距离的最大值，是圆的重要属性之一。

当我们知道圆的半径或直径时，我们可以通过公式计算出圆的周长和面积。

圆的周长是指圆周的长度，可以使用公式C = πd或C =2πr计算，其中C表示周长，d表示直径，r表示半径，π是一个常数，约为3.14159。

圆的面积是指圆内部的面积，可以使用公式A =πr^2计算，其中A表示面积。

其次，我们需要了解圆周率π的概念。

圆周率是圆的周长和直径比值，是一个无理数，其数值约为3.14159。

圆周率是圆的重要属性之一，是数学中的一个重要常数。

使用圆周率可以方便我们计算圆的周长和面积，是学习圆的重要基础知识。

最后，我们需要重点掌握圆的面积和周长的关系。

当我们使用圆周率π、半径或直径计算圆的周长和面积时，会发现其计算公式中均包含圆周率π。

这是因为圆的周长和面积和圆周率π密切相关。

当我们知道圆周率π和半径或直径时，就可以方便地计算出圆的周长和面积。

总之，圆的面积和周长是圆的基本属性之一。

当我们学习圆时，需要掌握圆的基本概念、圆周率π的概念以及圆的面积和周长的关系。

通过理解和掌握这些知识，我们可以更加深入地了解圆的性质和特点，为进一步学习几何学打下坚实的基础。

圆的面积与周长圆是一种非常特殊的几何形状，具有许多独特的性质。

在圆的性质中，面积和周长是非常重要的参数。

本文将探讨圆的面积和周长之间的关系，并介绍相关的公式和计算方法。

一、圆的面积圆的面积是指圆所包含的平面上的所有点构成的区域的大小。

要计算圆的面积，我们需要知道圆的半径或直径。

1. 圆的半径（r）：圆心到圆周上任意一点的距离。

2. 圆的直径（d）：通过圆心的一条线段，两端点都在圆上。

圆的面积公式为：S = πr² 或S = π(d/2)²，其中π是一个常数，近似值约为3.14159。

假设有一个半径为r的圆，其面积可以通过公式S = πr²来计算。

举个例子，假设一个圆的半径为5厘米，那么它的面积就是S = π(5²) = 25π平方厘米。

二、圆的周长圆的周长是指圆周上的线段的长度，也可以称为圆的周长。

要计算圆的周长，我们同样需要知道圆的半径或直径。

圆的周长公式为：C = 2πr 或C = πd，其中C表示圆的周长。

假设有一个半径为r的圆，其周长可以通过公式C = 2πr来计算。

举个例子，假设一个圆的半径为5厘米，那么它的周长就是C =2π(5) = 10π厘米。

三、圆的面积与周长的关系圆的面积和周长之间有一个特殊的关系，即当半径增加时，面积增加，周长也相应增加。

我们知道，圆的直径是半径的两倍，所以圆的周长可以表示为C = 2πr = πd。

可以看出，周长与半径（或直径）成正比。

而圆的面积公式为S = πr²，可以看出，面积与半径（或直径）的平方成正比。

因此，当半径增加时，面积的增加速度比周长更快。

这个关系在许多实际问题中都具有重要的意义，例如建筑设计、地理测量等领域。

四、计算实例为了进一步理解圆的面积和周长的关系，以下是几个计算实例：1. 已知圆的半径为3厘米，求其面积和周长。

解：根据公式S = πr²，我们可以计算出面积S = π(3²) = 9π平方厘米；根据公式C = 2πr，我们可以计算出周长C = 2π(3) = 6π厘米。