王式安-概率论与数理统计讲义
- 格式:pdf
- 大小:5.00 MB
- 文档页数:47

概率论与数理统计讲义稿HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】第一章随机事件与概率§1.1 随机事件1.1.1 随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只一个,且都是事先可以知道的;(3)每一次试验都会出现上述可能结果中的某一个结果,至于是哪一个结果则事前无法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英文字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别用希腊字母ω和Ω表示样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的目的。
假设抛掷一枚硬币两次,出于某些目的,也许只需要考虑三种可能的结果就足够了,两次都是正面,两次都是反面,一次是正面一次是反面。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反面的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正面-正面、反面-反面、正面-反面、反面-正面。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使用比绝对必要的样本空间较大的样本空间,因为它便于使用。
比如,在前面的例子中,由四个可能结果组成的样本空间便于问题的讨论,因为对于一个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
E:从最简单的试验开始,这些试验只有两种结果。
在抛掷硬币这一试验例1.1.11中出现“正面”或“反面”;在检查零件质量时,可能是“合格”或“不合格”;当用来模拟电子产品旋转的方向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正面,反面}。
E:更复杂一些,有的随机试验会产生多种可能的结果,比如掷一颗骰子,观察出2现的点数。

第一章随机事件与概率§1.1 随机事件1.1.1 随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只一个,且都是事先可以知道的;(3)每一次试验都会出现上述可能结果中的某一个结果,至于是哪一个结果则事前无法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英文字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别用希腊字母ω和Ω表示样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的目的。
假设抛掷一枚硬币两次,出于某些目的,也许只需要考虑三种可能的结果就足够了,两次都是正面,两次都是反面,一次是正面一次是反面。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反面的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正面-正面、反面-反面、正面-反面、反面-正面。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使用比绝对必要的样本空间较大的样本空间,因为它便于使用。
比如,在前面的例子中,由四个可能结果组成的样本空间便于问题的讨论,因为对于一个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
例1.1.1E:从最简单的试验开始,这些试验只有两种结果。
在抛掷硬币这1一试验中出现“正面”或“反面”;在检查零件质量时,可能是“合格”或“不合格”;当用来模拟电子产品旋转的方向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正面,反面}。
E:更复杂一些,有的随机试验会产生多种可能的结果,比如掷一颗骰子,2观察出现的点数。
样本空间为:{1,2,3,4,5,6}Ω=。
E: 掷两枚硬币(或者观察两个零件或两个电子产品),可以得到3Ω={(正面,正面)、(反面,反面)、(正面,反面)、(反面,正面)} 读者可以将其推广到掷n个硬币,样本空间里有多少样本点呢?E:再复杂一些,一名射手向某目标射击,直至命中目标为止,观察其命中目4标所进行的射击次数。


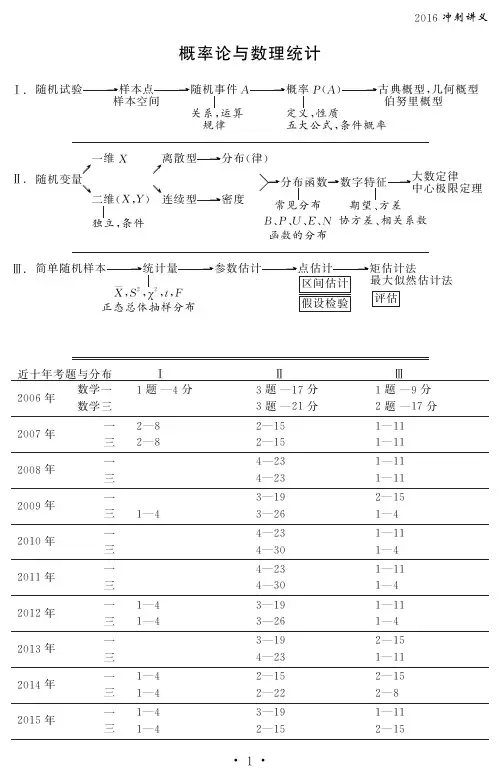


第一章 随机事件和概率 第一节 基本概念1、排列组合初步(1)排列组合公式)!(!n m m P n m -= 从m 个人中挑出n 个人进行排列的可能数。
)!(!!n m n m C n m -=从m 个人中挑出n 个人进行组合的可能数。
例1.1:方程xx x C C C 76510711=-的解是 A . 4 B . 3 C . 2 D . 1例1.2:有5个队伍参加了甲A 联赛,两两之间进行循环赛两场,试问总共的场次是多少?(2)加法原理(两种方法均能完成此事):m+n某件事由两种方法来完成,第一种方法可由m 种方法完成,第二种方法可由n 种方法来完成,则这件事可由m+n 种方法来完成。
(3)乘法原理(两个步骤分别不能完成这件事):m ×n某件事由两个步骤来完成,第一个步骤可由m 种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m ×n 种方法来完成。
例1.3:从5位男同学和4位女同学中选出4位参加一个座谈会,要求与会成员中既有男同学又有女同学,有几种不同的选法?例1.4:6张同排连号的电影票,分给3名男生和3名女生,如欲男女相间而坐,则不同的分法数为多少?例1.5:用五种不同的颜色涂在右图中四个区域里,每一区域涂上一种颜色,且相邻区域的颜色必须不同,则共有不同的涂法A.120种B.140种 C.160种D.180种(4)一些常见排列①特殊排列②相邻③彼此隔开④顺序一定和不可分辨例1.6:晚会上有5个不同的唱歌节目和3个不同的舞蹈节目,问:分别按以下要求各可排出几种不同的节目单?①3个舞蹈节目排在一起;②3个舞蹈节目彼此隔开;③3个舞蹈节目先后顺序一定。
例1.7:4幅大小不同的画,要求两幅最大的排在一起,问有多少种排法?例1.8:5辆车排成1排,1辆黄色,1辆蓝色,3辆红色,且3辆红车不可分辨,问有多少种排法?①重复排列和非重复排列(有序)例1.9:5封不同的信,有6个信箱可供投递,共有多少种投信的方法?②对立事件例1.10:七人并坐,甲不坐首位,乙不坐末位,有几种不同的坐法?例1.11:15人中取5人,有3个不能都取,有多少种取法?例1.12:有4对人,组成一个3人小组,不能从任意一对中取2个,问有多少种可能性?③ 顺序问题例1.13:3白球,2黑球,先后取2球,放回,2白的种数?(有序) 例1.14:3白球,2黑球,先后取2球,不放回,2白的种数?(有序) 例1.15:3白球,2黑球,任取2球,2白的种数?(无序)2、随机试验、随机事件及其运算(1)随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验。

王式安概率论必背积分公式 -回复王式安概率论必背积分公式在概率论领域中具有重要的作用,它能够帮助我们更好地理解和分析各种概率事件的发生概率。
在本文中,我们将深入探讨王式安概率论必背积分公式的相关知识,并结合具体的例子来解释其应用。
通过阅读本文,读者将能够全面理解和掌握这一重要的概念。
1. 王式安概率论必背积分公式的定义王式安概率论必背积分公式是概率论中的重要公式之一,它用于计算随机变量的概率分布函数。
具体表达式如下:[ P(X x) = _{-}^{x} f(u) du ]其中,( X ) 表示随机变量,( x ) 表示特定的取值,( f(u) ) 表示随机变量的概率密度函数。
2. 理解王式安概率论必背积分公式王式安概率论必背积分公式通过积分的方式来计算随机变量小于等于某一特定取值的概率。
这样的公式能够帮助我们更好地理解随机变量的分布规律,并能够应用在诸如连续型随机变量的概率计算中。
举个简单的例子来说明,假设有一个连续型随机变量X,其概率密度函数为( f(x) = 3x^2, 0 <= x <= 1 )。
那么,当我们想要计算随机变量X小于等于0.5的概率时,可以利用王式安概率论必背积分公式进行计算。
具体来说,就是将概率密度函数带入积分公式,进行积分计算即可得到结果。
3. 王式安概率论必背积分公式的应用王式安概率论必背积分公式在概率论领域中有着广泛的应用,特别是在连续型随机变量分布函数的计算中。
通过这一公式,我们可以更准确地计算各种随机变量的概率分布,从而更好地理解和分析概率事件的发生规律。
除了在理论研究中的应用外,王式安概率论必背积分公式也在实际问题的建模和求解中发挥着重要作用。
比如在金融领域中,利用概率密度函数和分布函数来描述资产价格的波动,从而进行风险管理和投资决策。
4. 个人观点和总结王式安概率论必背积分公式作为概率论中的重要工具,对于我们理解和分析各种随机事件的发生概率具有重要意义。



概率论与数理统计讲义稿第⼀章随机事件与概率§1.1 随机事件1.1.1 随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只⼀个,且都是事先可以知道的;(3)每⼀次试验都会出现上述可能结果中的某⼀个结果,⾄于是哪⼀个结果则事前⽆法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英⽂字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别⽤希腊字母ω和Ω表⽰样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的⽬的。
假设抛掷⼀枚硬币两次,出于某些⽬的,也许只需要考虑三种可能的结果就⾜够了,两次都是正⾯,两次都是反⾯,⼀次是正⾯⼀次是反⾯。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反⾯的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正⾯-正⾯、反⾯-反⾯、正⾯-反⾯、反⾯-正⾯。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使⽤⽐绝对必要的样本空间较⼤的样本空间,因为它便于使⽤。
⽐如,在前⾯的例⼦中,由四个可能结果组成的样本空间便于问题的讨论,因为对于⼀个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
例 1.1.1 1E :从最简单的试验开始,这些试验只有两种结果。
在抛掷硬币这⼀试验中出现“正⾯”或“反⾯”;在检查零件质量时,可能是“合格”或“不合格”;当⽤来模拟电⼦产品旋转的⽅向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正⾯,反⾯}。
2E :更复杂⼀些,有的随机试验会产⽣多种可能的结果,⽐如掷⼀颗骰⼦,观察出现的点数。
样本空间为:{1,2,3,4,5,6}Ω=。
3E : 掷两枚硬币(或者观察两个零件或两个电⼦产品),可以得到Ω={(正⾯,正⾯)、(反⾯,反⾯)、(正⾯,反⾯)、(反⾯,正⾯) }读者可以将其推⼴到掷n 个硬币,样本空间⾥有多少样本点呢?4E :再复杂⼀些,⼀名射⼿向某⽬标射击,直⾄命中⽬标为⽌,观察其命中⽬标所进⾏的射击次数。
概率论与数理统计讲义稿Company number:【0089WT-8898YT-W8CCB-BUUT-202108】第一章随机事件与概率§随机事件随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只一个,且都是事先可以知道的;(3)每一次试验都会出现上述可能结果中的某一个结果,至于是哪一个结果则事前无法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英文字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别用希腊字母ω和Ω表示样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的目的。
假设抛掷一枚硬币两次,出于某些目的,也许只需要考虑三种可能的结果就足够了,两次都是正面,两次都是反面,一次是正面一次是反面。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反面的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正面-正面、反面-反面、正面-反面、反面-正面。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使用比绝对必要的样本空间较大的样本空间,因为它便于使用。
比如,在前面的例子中,由四个可能结果组成的样本空间便于问题的讨论,因为对于一个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
E:从最简单的试验开始,这些试验只有两种结果。
在抛掷硬币这一试验中出例1现“正面”或“反面”;在检查零件质量时,可能是“合格”或“不合格”;当用来模拟电子产品旋转的方向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正面,反面}。
2E :更复杂一些,有的随机试验会产生多种可能的结果,比如掷一颗骰子,观察出现的点数。
样本空间为:{1,2,3,4,5,6}Ω=。
第一章随机事件与概率§随机事件随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只一个,且都是事先可以知道的;(3)每一次试验都会出现上述可能结果中的某一个结果,至于是哪一个结果则事前无法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英文字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别用希腊字母ω和Ω表示样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的目的。
假设抛掷一枚硬币两次,出于某些目的,也许只需要考虑三种可能的结果就足够了,两次都是正面,两次都是反面,一次是正面一次是反面。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反面的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正面-正面、反面-反面、正面-反面、反面-正面。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使用比绝对必要的样本空间较大的样本空间,因为它便于使用。
比如,在前面的例子中,由四个可能结果组成的样本空间便于问题的讨论,因为对于一个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
E:从最简单的试验开始,这些试验只有两种结果。
在抛掷硬币这一试验中例1出现“正面”或“反面”;在检查零件质量时,可能是“合格”或“不合格”;当用来模拟电子产品旋转的方向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正面,反面}。
E:更复杂一些,有的随机试验会产生多种可能的结果,比如掷一颗骰子,观察2出现的点数。
样本空间为:{1,2,3,4,5,6}Ω=。
E: 掷两枚硬币(或者观察两个零件或两个电子产品),可以得到3Ω={(正面,正面)、(反面,反面)、(正面,反面)、(反面,正面)}读者可以将其推广到掷n个硬币,样本空间里有多少样本点呢?E:再复杂一些,一名射手向某目标射击,直至命中目标为止,观察其命中目标所4进行的射击次数。
概率论与数理统计讲义稿-CAL-FENGHAI.-(YICAI)-Company One1第一章随机事件与概率§1.1 随机事件1.1.1 随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只一个,且都是事先可以知道的;(3)每一次试验都会出现上述可能结果中的某一个结果,至于是哪一个结果则事前无法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英文字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别用希腊字母ω和Ω表示样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的目的。
假设抛掷一枚硬币两次,出于某些目的,也许只需要考虑三种可能的结果就足够了,两次都是正面,两次都是反面,一次是正面一次是反面。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反面的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正面-正面、反面-反面、正面-反面、反面-正面。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使用比绝对必要的样本空间较大的样本空间,因为它便于使用。
比如,在前面的例子中,由四个可能结果组成的样本空间便于问题的讨论,因为对于一个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
E:从最简单的试验开始,这些试验只有两种结果。
在抛掷硬例1.1.11币这一试验中出现“正面”或“反面”;在检查零件质量时,可能是“合格”或“不合格”;当用来模拟电子产品旋转的方向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正面,反面}。
E:更复杂一些,有的随机试验会产生多种可能的结果,比如掷一颗骰2子,观察出现的点数。
样本空间为:{1,2,3,4,5,6}Ω=。