节约里程法
- 格式：doc
- 大小：403.50 KB
- 文档页数：7
下载文档原格式
合集下载
物流工程——节约里程法
物流配送——节约里程法(Saving Algorithm)
• 车辆调度程序法(Vehicle Scheduling Program:VSP) • 又称节约算法，是指用来解决运输车辆数目不确定的问题 的最有名的启发式算法。 核心思想: • 节约里程法核心思想是依次将运输问题中的两个回路合并 为一个回路，每次使合并后的总运输距离减小的幅度最大， 直到达到一辆车的装载限制时，再进行下一辆车的优化。 优化过程分为并行方式和串行方式两种。
（0.9）
P3
4
P2
以此类推，如果前面涉及了某些 路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
（1.7）
5
6 8
（1.4）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
5
（0.9）
P3
4
P2
（1.7）
配送线路1
（1.4）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
案例： • 宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见 下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优 化方法。公司客户分布在全国各地,这里主要以广东省内7家客户 及省外一家特殊客户的一次配送为例。
客户(i) 货运量 (qi) 东莞 江门 4.3 1.8 惠州 0.7 阳江 2.2 汕尾 3.6 揭阳 3.6 汕头 1.6 漳州 2
（2.4）
节约里程法
（0.9）
P3
（1.7）
P2
6 8
（1.4）
• 车辆调度程序法(Vehicle Scheduling Program:VSP) • 又称节约算法，是指用来解决运输车辆数目不确定的问题 的最有名的启发式算法。 核心思想: • 节约里程法核心思想是依次将运输问题中的两个回路合并 为一个回路，每次使合并后的总运输距离减小的幅度最大， 直到达到一辆车的装载限制时，再进行下一辆车的优化。 优化过程分为并行方式和串行方式两种。
（0.9）
P3
4
P2
以此类推，如果前面涉及了某些 路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
（1.7）
5
6 8
（1.4）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
5
（0.9）
P3
4
P2
（1.7）
配送线路1
（1.4）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
案例： • 宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见 下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优 化方法。公司客户分布在全国各地,这里主要以广东省内7家客户 及省外一家特殊客户的一次配送为例。
客户(i) 货运量 (qi) 东莞 江门 4.3 1.8 惠州 0.7 阳江 2.2 汕尾 3.6 揭阳 3.6 汕头 1.6 漳州 2
（2.4）
节约里程法
（0.9）
P3
（1.7）
P2
6 8
（1.4）
节约里程法PPT课件
的使用率和周转率。
实施效果
通过节约里程法的应用，共享单 车的调度系统得到了优化，高峰 时段的供不应求问题得到了缓解， 提高了共享单车的服务质量和用
户体验。
06
总结与展望
总结节约里程法的原理与应用
要点一
总结
要点二
应用
节约里程法的原理是基于车辆运输路径优化，通过合理安 排车辆行驶路线，减少车辆空驶和重复行驶的距离，达到 降低运输成本和提高运输效率的目的。在实际应用中，该 方法广泛应用于物流配送、公共交通和共享出行等领域。
节约里程法的应用场景
物流配送路线规划
总结词
节约里程法在物流配送路线规划中，能够优化车辆行驶路径，减少运输成本和 时间。
详细描述
通过计算各需求点之间的距离节约量，选择最佳的配送路线，使得车辆在满足 客户需求的同时，总行驶距离最短，从而达到节约成本和时间的目的。
公共交通路线规划
总结词
节约里程法在公共交通路线规划中， 能够提高线路效率和乘客出行体验。
里程法更注重求解的稳定性。
05
节约里程法的实际案例分 析
某快递公司的配送路线优化
01
02
03
背景介绍
某快递公司面临配送路线 不优化、成本高昂的问题， 需要采用节约里程法进行 配送路线的优化。
解决方案
利用节约里程法，对快递 公司的配送路线进行重新 规划，减少重复行驶和空 驶，提高车辆装载率。
实施效果
低运输成本。
它主要应用于多个发货点之间， 通过合并多个货物装载在同一辆
车上，实现运输效率最大化。
节约里程法的基本思想是通过优 化运输路线，减少车辆空驶和重 复行驶，提高运输效率，降低运
输成本。
适用范围与条件
实施效果
通过节约里程法的应用，共享单 车的调度系统得到了优化，高峰 时段的供不应求问题得到了缓解， 提高了共享单车的服务质量和用
户体验。
06
总结与展望
总结节约里程法的原理与应用
要点一
总结
要点二
应用
节约里程法的原理是基于车辆运输路径优化，通过合理安 排车辆行驶路线，减少车辆空驶和重复行驶的距离，达到 降低运输成本和提高运输效率的目的。在实际应用中，该 方法广泛应用于物流配送、公共交通和共享出行等领域。
节约里程法的应用场景
物流配送路线规划
总结词
节约里程法在物流配送路线规划中，能够优化车辆行驶路径，减少运输成本和 时间。
详细描述
通过计算各需求点之间的距离节约量，选择最佳的配送路线，使得车辆在满足 客户需求的同时，总行驶距离最短，从而达到节约成本和时间的目的。
公共交通路线规划
总结词
节约里程法在公共交通路线规划中， 能够提高线路效率和乘客出行体验。
里程法更注重求解的稳定性。
05
节约里程法的实际案例分 析
某快递公司的配送路线优化
01
02
03
背景介绍
某快递公司面临配送路线 不优化、成本高昂的问题， 需要采用节约里程法进行 配送路线的优化。
解决方案
利用节约里程法，对快递 公司的配送路线进行重新 规划，减少重复行驶和空 驶，提高车辆装载率。
实施效果
低运输成本。
它主要应用于多个发货点之间， 通过合并多个货物装载在同一辆
车上，实现运输效率最大化。
节约里程法的基本思想是通过优 化运输路线，减少车辆空驶和重 复行驶，提高运输效率，降低运
输成本。
适用范围与条件
节约里程法
第一步：计算最短距离。根据配送网络中的已知条件， 计算配送中心与客户及客户之间的最短距离，结果见表 11-11。 第二步：计算节约里程sij,结果见表11-12。
第三步：将节约sij,进行分类，按从大到小的顺序排 列，得表11-13
第四步：确定配送线路。从分类表中，按节约里程大小顺序，组成线路图
第三步考察S(i,j)对应的点i和j，检查是否满足下列条件。
若点i和j均不在已构成的线路上，则可连接点i和j，得到线路段0-i-j-0，转 第四步；
若点i和j在已构成的线路上，但不是线路的内点（即不与配送中心0直接 相连）。则可以连接，连接后得到线路0…-i-j-0,或0- i-j-…0，转第四
0.4
0.8
d
5
c
5
6
1.4
9
e
8
8
7
9
10
7
10
8
Q
7
f
3
4
1.5
6
g
0.6 2
h
0.8
配送网络图
1.5
b
4 0.7
a
4
0.6
11
j
10
8
i
9 0.5
第一步：选择初始方案：从Q点向各点分别派车送货。
第二步：作出最短距离矩阵，从配送网络图中
列出配送中心至用户相互间的最短距离矩阵 。
P0
P1 10 P1
顺序排位
1 2 3 4 4 6 6 6 9 9 11 12
连接线
A－B A－J B－C D－E C－D A－I E－F I－J A－C B－J B－D C－E
节约里程
15 13 11 10 10 9 9 9 8 8 7 6
节约里程法计算步骤
节约里程法计算步骤节约里程法是一种常用的路径规划方法，可以帮助人们在行程中选择最经济、最节约的路线。
它的原理是通过计算不同路径的总里程数，然后选择总里程最短的路径作为最佳行驶路线。
下面将介绍一下节约里程法的具体计算步骤。
1. 确定起点和终点在使用节约里程法进行路径规划之前，首先需要明确起点和终点的位置。
起点是出发地点，终点是目的地。
这两个位置可以通过地图或者其他导航工具确定。
2. 划分路径将整个行程划分为多个路径段，每个路径段是相邻两个关键点之间的路段。
关键点可以是交叉口、转弯点或者其他有特殊意义的地点。
路径段的划分可以根据实际情况进行调整，一般情况下，路径段的长度不宜过长，也不宜过短。
3. 计算路径段的里程对于每个路径段，需要计算其对应的里程数。
里程数可以通过地图测距工具或者导航软件进行计算，也可以通过实际驾驶或者步行测量得出。
在计算里程数时，需要考虑道路的实际情况，包括拥堵、道路类型等因素。
4. 计算总里程将所有路径段的里程数相加，得到总里程数。
这个总里程数就是整个行程的里程数。
5. 比较总里程如果有多个可选路径，需要将它们的总里程进行比较。
选择总里程最短的路径作为最佳行驶路线。
在比较总里程时，需要考虑到实际情况，比如是否有收费站、是否有交通拥堵等因素。
6. 考虑其他因素除了总里程之外，还应该考虑其他因素对路径选择的影响。
比如时间、费用、景点等因素都可以作为选择路径的参考依据。
在实际行驶中，人们往往会根据自己的需求和偏好来做出最终决策。
通过以上步骤，我们可以使用节约里程法来计算行程的最佳路线。
这种方法可以帮助人们选择最经济、最节约的路径，减少行驶里程，节省时间和费用。
在实际应用中，我们可以根据需要进行适当的调整和优化，以满足不同的需求和条件。
无论是驾车还是步行，节约里程法都是一种实用的路径规划方法，可以帮助我们更加高效地完成出行计划。
节约里程法
定义节约里程法又称节约算法或节约法，是指用来解决运输车辆数目不确定的问题的最有名的启发式算法。
[1]2核心思想节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
[1]3基本规定利用节约法确定配送路线的主要出发点是，根据配送中心的运输能力和配送中心到各个用户以及各个用户之间的距离来制定使总的车辆运输的吨公里数最小的配送方案。
另还需满足以下条件；（1）所有用户的要求；（2）不使任何一辆车超载；（3）每辆车每天的总运行时间或行驶里程不超过规定的上限；（4）用户到货时间要求。
[2]4基本思想为达到高效率的配送，使配送的时间最小距离最短成本最低，而寻找的最佳配送路线。
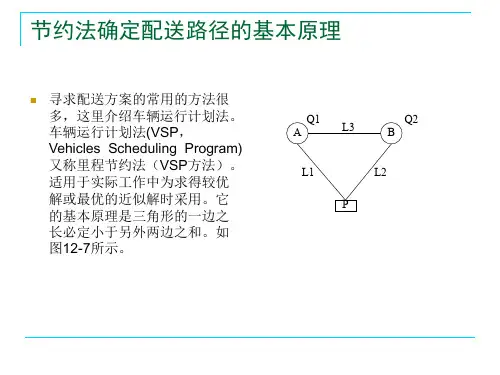
[2]5典型例题例题：已知配送中心P0向5个用户Pj配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图所示，配送中心有3台2t卡车和2台4t两种车辆可供使用。
利用节约里程法制定最优的配送方案。
[1]节约里程法例题用图第一步，作运输里程表，列出配送中心到用户及用户建的最短距离。
[1]第二步，按节约里程公式求得相应的节约里程数。
[1]第三步，将节约里程按从大到小顺序排列。
[1]第四步，根据载重量约束与节约里程大小，顺序连接各客户结点，形成两个配送线。
[1]P2P3－P3P4－P2P4－P4P5－P1P2－P1P5－P1P3－P2P5－P3P5－P1P4得出结果：配送线路一：运量=1.7+0.9+1.4=4t运行距离=8+4+5+7=24km用一辆4t车运送，节约距离为18km 配送线路二：运量=2.4+1.5=3.9t<4t运行距离=8+10+16=34km用一辆4t车运送，节约距离为2km[1]初始方案：配送线路5条，需要车5辆，配送距离=39*2=78km 优化后的方案：2条配送路线,2辆4t车，配送距离=24+34=78km[1]。
节约里程法介绍
一、6.车辆的装载技术
车辆合理调度的方法：
经验调度法：在能够保证满载的情况下，优先使用大型车辆，且先 载运大批量的货物。
运输定额比法：车辆的运送能力计算每种车运送不同的定额比。
二、配送路线优化设计方法——节约里程法
二、1.节约里程算法基本原理
• 基本原理是几何学中三角形一边之长必定小于另外两边之和。 • 节约里程法核心思想是依次将运输问题中的两个回路合并为一个回
节约里程法讲解
配送路线设计——节约里程法
一、1.配送路线设计说明
• 随着小批量多批次的及时配送的发展，物流配送费用正在逐年提升， 选择有效的的配送路线，已经成为控制物流成本的主要措施！
• 什么是有效的配送路线？ ✓ 有效的配送路线，实际上是保证货物准时到达客户指定地前提下，尽
可能的减少运输的车次和运输的总路程，在这种思想下，节约里程法 已经成为选择配送路线的主要方法。
二、2.案例分析：
• 例：由配送中心P向A—I等9个用户配送货物。图中连线 上的数字表示公路里程（km）ቤተ መጻሕፍቲ ባይዱ靠近各用户括号内的数 字，表示各用户对货物的需求量（t）。配送中心备有2t 和4t载重量的汽车，且汽车一次巡回走行里程不能超过 35km，设送到时间均符合用户要求，求该配送中心的最 优送货方案。
一、1.配送路线设计说明
通常认为，配送是近距离，小批量，品种比较复杂，按用户需要搭配 品种与数量的服务体系；从配送中心把货物送到所需要的各个用户， 有很多不同的路线选择方案。合理的选择配送路线，对企业和社会具 有很重要的意义： 优化配送路线，可以提高配送效率，对配送车辆做到 物尽其用尽可能的降低配送成本。 可以准时、快速地把货物送到客户的手中，能极大地提高 客 户满意度。 有利于企业提高效益。 对社会而言，它可以节省运输车辆，缓解交通紧张状况，减少噪音、 尾气排放等运输污染，为保护生态平衡、创造美好家园做出贡献。
节约里程法
节约里程法计算步骤
4、规划路线（考虑货车载重量和距离限制）
A 1.75 1.1 E 1.15 F G
路线1
1.75 + 1.15+1.1 = 4 全程长度：20+1+6+24=51
路线2
A
B
0.8 C 0.7
1.0 D 1.0+0.7+0.8=2.5 全程长度：9+9+10+12=40
节约法确定配送路径的基本原理
寻求配送方案的常用的方法很 多，这里介绍车辆运行计划法。 车辆运行计划法(VSP， Vehicles Scheduling Program) 又称里程节约法（VSP方法）。 适用于实际工作中为求得较优 解或最优的近似解时采用。它 的基本原理是三角形的一边之 长必定小于另外两边之和。如 图12-7所示。
5、计算总里程 51+40=91千米
案例12- 3：里程节约法确定配送路径
如图12-8所示某配送中心的配送网络图。由配送中心P向A、B、C、 D、E等五个用户配送物品。图中连线上的数字表示公路里程（km）。 图中靠近各用户括号里的数字，表示对货物的需求量（t）。配送中心 备有2t和4t载质量的汽车，且汽车一次巡回行驶里程不能超过30km。 求解该配送中心满意的送货方案。
节约里程法计算步骤
1、计算配送中心A到各配送点，各配送点之间的最短距离。
A A B C D E F G 0
B 9 0
C 12 9 0
D 12 19 10 0
E 20 29 32 25 0
F 24 33 29 19 6 0
G 21 30 33 25 1 6 0
节约里程法
客户(i) 东莞 江门 惠州 阳江 汕尾 揭阳 汕头 漳州
货运量 4.3 1.8 0.7 2.2 3.6 3.6 1.6 2 (qi)
节约里程法
• 广州配送中心为这次配送提供了三种车型,载重量分别为2 吨、5吨和8吨,不同车型的运输单价不一样,具体见运输单 价表。配送中心的配送是由外协商提供车辆,因此汽车的 数量没有限制
节约距离 =18km
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 节约距离=2km
节约里程法
（0.9）
P3
6
（1.4）
P4
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
初始方案：配送线路5条， 需要车5辆 配送距离=39×2=78KM
P1 (1.5)
节约里程法
第六步:最终方案的确定。
节约里程法
• 最终修改后的车辆调度结果：
节约里程法
• 通过对比初始方案与最终方案可知,通过优化可节约里程 (1768-1047)=721(公里),节约成本(4476.33384.55)=1091.75(元),仅8家客户的一次配送就节约了物 流配送成本1091.75。
• 车辆载重
2T 5T 8T
• 运价(元/公里) 2.4 2.7 3.65
节约里程法
2.步骤 第一步:各城市之间的距离：
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法
第三步:确定初始方案的运输线路及运输费用,现安排4辆2吨、4辆5吨的车给 每个客户送货。运输线路及运输费用见下表所示。
5
P1P2
货运量 4.3 1.8 0.7 2.2 3.6 3.6 1.6 2 (qi)
节约里程法
• 广州配送中心为这次配送提供了三种车型,载重量分别为2 吨、5吨和8吨,不同车型的运输单价不一样,具体见运输单 价表。配送中心的配送是由外协商提供车辆,因此汽车的 数量没有限制
节约距离 =18km
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 节约距离=2km
节约里程法
（0.9）
P3
6
（1.4）
P4
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
初始方案：配送线路5条， 需要车5辆 配送距离=39×2=78KM
P1 (1.5)
节约里程法
第六步:最终方案的确定。
节约里程法
• 最终修改后的车辆调度结果：
节约里程法
• 通过对比初始方案与最终方案可知,通过优化可节约里程 (1768-1047)=721(公里),节约成本(4476.33384.55)=1091.75(元),仅8家客户的一次配送就节约了物 流配送成本1091.75。
• 车辆载重
2T 5T 8T
• 运价(元/公里) 2.4 2.7 3.65
节约里程法
2.步骤 第一步:各城市之间的距离：
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法
第三步:确定初始方案的运输线路及运输费用,现安排4辆2吨、4辆5吨的车给 每个客户送货。运输线路及运输费用见下表所示。
5
P1P2
节约里程法
P2
5
6 8
（1.4） ）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4） ）
节约里程法
（0.9） ）
P3
4
（1.7） ）
P2
5 配送线路1
（1.4） ）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4） ）
（0.9） ）
节约里程法
5
P3
4
P2
（1.7） ）
配送线路1
（1.4） ）
P4
8
7
P0
10
8
P5
P
(配送中心)
b
B（客户）
运行距离为：2a+2b 节约行程： 节约行程#43;c
节约里程法
例题：已知配送中心P0向5个用户Pj配送货物，其配送路线网 络、配送中心与用户的距离以及用户之间的距离如下图所 示，配送中心有3台2t卡车和2台4t两种车辆可供使用。利 用节约里程法制定最优的配送方案。 ( 0.9 )
节约里程法
• 利用节约法制定出的配送方案除了使配送总吨公 里数最小外，还应满足以下条件：
– 满足所有用户的需求 –不使任何一辆车超载 –每辆车每天的总运行时间或行驶里程不超过规定的上 限； –用户到货时间要求。不得超过规定时间。
节约里程法
A（客户）
a a c
A（客户）
P
(配送中心) b
B（客户）
P1
(1.5)
（2.4） ）
配送线路2: 配送线路1： 运量=2.4+1.5=3.9t<4t 运量 = 1.7+0.9+1.4= 4t 运行距离＝8＋4＋5＋7＝24km 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 用一辆 4t车运送 节约距离=2km 节约距离 =18km
5
6 8
（1.4） ）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4） ）
节约里程法
（0.9） ）
P3
4
（1.7） ）
P2
5 配送线路1
（1.4） ）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4） ）
（0.9） ）
节约里程法
5
P3
4
P2
（1.7） ）
配送线路1
（1.4） ）
P4
8
7
P0
10
8
P5
P
(配送中心)
b
B（客户）
运行距离为：2a+2b 节约行程： 节约行程#43;c
节约里程法
例题：已知配送中心P0向5个用户Pj配送货物，其配送路线网 络、配送中心与用户的距离以及用户之间的距离如下图所 示，配送中心有3台2t卡车和2台4t两种车辆可供使用。利 用节约里程法制定最优的配送方案。 ( 0.9 )
节约里程法
• 利用节约法制定出的配送方案除了使配送总吨公 里数最小外，还应满足以下条件：
– 满足所有用户的需求 –不使任何一辆车超载 –每辆车每天的总运行时间或行驶里程不超过规定的上 限； –用户到货时间要求。不得超过规定时间。
节约里程法
A（客户）
a a c
A（客户）
P
(配送中心) b
B（客户）
P1
(1.5)
（2.4） ）
配送线路2: 配送线路1： 运量=2.4+1.5=3.9t<4t 运量 = 1.7+0.9+1.4= 4t 运行距离＝8＋4＋5＋7＝24km 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 用一辆 4t车运送 节约距离=2km 节约距离 =18km
节约里程法
b94b
c795c
d 8 14 10 5 d
e 8 18 14 9 6 e
f 8 18 17 15 13 7 f
g 3 13 12 10 11 10 6 g
h 4 14 13 11 12 12 8 2 h
i 10 11 15 17 18 18 17 11 9 i
ห้องสมุดไป่ตู้
j 7 4 8 13 15 15 15 10 11 8 j
5
5
d
c
b4
6
a
e
4
7 8
7 Q
j
f
3
10
g
h
2
9
i
最佳配送线路
8
配送线路的优化
节约里程法 1、节约里程的基本原理
用一辆车将所有客户的货物装在一起，沿着一条精心 选择的最佳路线，将货物送到客户手中。 目标：节约车辆、节约费用、缓解交通压力、减少环 境污染。
△S = S1 + S2 - S3
1
2、按节约里程法制定配送计划 例 有一配送中心（Q）要向10个用户配送，配送距离 （公里）和需用量（吨）如下图所示。 假设：采用最大载重量2吨、4吨、8吨三种汽车，并限 定车辆一次运行距离50公里。 用节约里程法选择最佳配送路线和车辆的调度。
j 13 8 1 0 0 0 0 0 9
节约里程计算过程
5
第四步：将节约里程按大小顺序排列分类。
节约里程顺序表
分类 Ⅰ
用户连接 线
a—b
节约里 程
15
分类 Ⅸ
用户连接 线
f—g
Ⅱ
a—j
13
Ⅸ
g—h
Ⅲ
b—c
11
节约里程法
=27+34=61(Km) 节约费用:C=(61/25)×45=109.8（元）
7
12 5
P5 （2.5） 9
（1.7） P2
4 8
P1 （2.8）
P0 19
11
（1.6）
P7 （1.8）
配送线路： ①P0→P2→P3→P4→P0（27Km）,派4t车1辆 ②P0→P5→P6→P7→P0(44Km),派6t车1辆 ③P0→P1→P0(16Km),派4t车1辆 节约里程数:△S=148－(27+44+16)=61(Km)
设配送中心P0向7个用户Pj配送货物，其配送路线网 络、配送中心与用户的距离以及用户之间的距离如下图1
与下表1所示，图中括号内的数字表示客户的需求量( 单位：t)，线路上的数字表示两结点之间的距离(单位 ：km)，现配送中心有2台4t卡车和2台6t卡车两种车辆 可供使用。
⑴试用节约里程法制定最优的配送方案。
O 图2
△L=L1－L2=2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c
2.节约里程法核心思想
节约里程法核心思想是依次将运输问题中的两个回路 合并为一个回路，每次使合并后的总运输距离减小的幅 度最大，直到达到一辆车的装载限制时，再进行下一辆 车的优化。
3.节约里程法的应用
⑵设配送中心在向用户配送货物过程中单位时间平均支 出成本为45元，假定卡车行驶的平均速度为25公里/ 小时，试比较优化后的方案比单独向各用户分送可节 约多少费用？
（0.8t）
P3
（1.7t） 4
5
P2
7
11
4
（1.4t）P4
12
10
7
12 5
P5 （2.5） 9
（1.7） P2
4 8
P1 （2.8）
P0 19
11
（1.6）
P7 （1.8）
配送线路： ①P0→P2→P3→P4→P0（27Km）,派4t车1辆 ②P0→P5→P6→P7→P0(44Km),派6t车1辆 ③P0→P1→P0(16Km),派4t车1辆 节约里程数:△S=148－(27+44+16)=61(Km)
设配送中心P0向7个用户Pj配送货物，其配送路线网 络、配送中心与用户的距离以及用户之间的距离如下图1
与下表1所示，图中括号内的数字表示客户的需求量( 单位：t)，线路上的数字表示两结点之间的距离(单位 ：km)，现配送中心有2台4t卡车和2台6t卡车两种车辆 可供使用。
⑴试用节约里程法制定最优的配送方案。
O 图2
△L=L1－L2=2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c
2.节约里程法核心思想
节约里程法核心思想是依次将运输问题中的两个回路 合并为一个回路，每次使合并后的总运输距离减小的幅 度最大，直到达到一辆车的装载限制时，再进行下一辆 车的优化。
3.节约里程法的应用
⑵设配送中心在向用户配送货物过程中单位时间平均支 出成本为45元，假定卡车行驶的平均速度为25公里/ 小时，试比较优化后的方案比单独向各用户分送可节 约多少费用？
（0.8t）
P3
（1.7t） 4
5
P2
7
11
4
（1.4t）P4
12
10
节约里程法的优化目标
节约里程法的优化目标【原创实用版】目录1.引言2.节约里程法的定义和意义3.节约里程法的优化目标4.节约里程法的实施策略5.节约里程法的效果评估6.结论正文【引言】随着社会经济的发展，资源浪费问题日益严重，特别是在交通运输领域，里程浪费现象普遍存在。
为了解决这一问题，节约里程法应运而生。
作为一种优化运输路线的方法，节约里程法旨在减少运输过程中的无效里程，提高运输效率，降低运输成本，从而实现资源节约和环境保护。
本文将从节约里程法的定义和意义、优化目标、实施策略和效果评估等方面进行阐述。
【节约里程法的定义和意义】节约里程法是一种优化运输路线的方法，主要通过减少运输过程中的无效里程，提高运输效率，降低运输成本，实现资源节约和环境保护。
在现代物流和交通运输领域，节约里程法具有重要的实用价值和意义。
【节约里程法的优化目标】节约里程法的优化目标是在保证运输质量和时效的前提下，通过优化运输路线，减少运输过程中的无效里程，提高运输效率，降低运输成本。
具体包括以下几个方面：1.最短路径：通过优化运输路线，使运输距离最短，从而减少无效里程。
2.最优路线：在保证运输质量和时效的前提下，选择最优的运输路线，降低运输成本。
3.资源整合：通过节约里程法，实现运输资源的整合，提高运输效率，降低空驶率。
【节约里程法的实施策略】要实现节约里程法的优化目标，需要采取一系列实施策略，包括：1.建立科学的运输网络：根据运输需求和资源分布，建立科学的运输网络，为节约里程法提供基础支持。
2.引入先进的运输规划技术：运用运输规划技术，如路径规划算法、遗传算法等，实现运输路线的优化。
3.建立健全的监测和管理体系：通过建立健全的监测和管理体系，对运输过程进行实时监控和调度，确保运输效率和质量。
【节约里程法的效果评估】节约里程法的效果评估主要从以下几个方面进行：1.运输距离的减少：通过比较实施节约里程法前后的运输距离，评估其效果。
2.运输成本的降低：通过比较实施节约里程法前后的运输成本，评估其效果。
两个例子-节约里程法
ቤተ መጻሕፍቲ ባይዱ原理
该方法基于节约思想，即在一辆运输车辆上装载多个客户的货物，通过合理规 划运输路线，使得车辆可以依次经过这些客户的所在地，并在满足车辆载重和 容量限制的前提下，实现运输里程的最小化。
发展历程及应用领域
发展历程
节约里程法最初由国外学者提出，后来经过不断改进和完善 ，逐渐形成了较为成熟的理论体系。目前，该方法已经在国 内外得到了广泛应用。
空间。
挑战
新技术的发展和应用需要大量的投入和研发，同时也需要面对技术更新换代快、数据安 全等问题。此外，新技术在节约里程法中的应用还需要与实际业务场景相结合，需要进
行不断的实践和调整。
行业应用拓展方向预测
物流行业
节约里程法在物流行业的应用已经比较成熟，未来可以进 一步拓展到智能物流、绿色物流等领域，实现更加高效、 环保的物流运输。
局限性
虽然节约里程法在优化运输路径方面具有一定的优势，但也存在一些局限性。例如，该方法只考虑了运输里程的 节约，而忽略了其他因素（如时间、服务质量等）对运输成本的影响。此外，在实际应用中，还需要考虑车辆的 载重和容量限制、道路状况、客户需求等多种因素，这也会增加该方法的复杂性和难度。
02 节约里程法实例一：物流 配送优化
01
节约里程法的时间复杂度主要取决于需求点的数量和合并运输的次数。
02
在需求点数量较多的情况下，算法可能需要较长的时间来寻找最优解。
03
为了优化算法，可以考虑采用启发式搜索策略，如贪婪算法、遗传算 法等，来加快搜索速度并提高解的质量。
04
此外，还可以考虑对需求点进行聚类处理，以减少合并运输的次数和 降低算法复杂度。
节约里程法在路线规划中应用
景点间距离与交通方式选择
该方法基于节约思想，即在一辆运输车辆上装载多个客户的货物，通过合理规 划运输路线，使得车辆可以依次经过这些客户的所在地，并在满足车辆载重和 容量限制的前提下，实现运输里程的最小化。
发展历程及应用领域
发展历程
节约里程法最初由国外学者提出，后来经过不断改进和完善 ，逐渐形成了较为成熟的理论体系。目前，该方法已经在国 内外得到了广泛应用。
空间。
挑战
新技术的发展和应用需要大量的投入和研发，同时也需要面对技术更新换代快、数据安 全等问题。此外，新技术在节约里程法中的应用还需要与实际业务场景相结合，需要进
行不断的实践和调整。
行业应用拓展方向预测
物流行业
节约里程法在物流行业的应用已经比较成熟，未来可以进 一步拓展到智能物流、绿色物流等领域，实现更加高效、 环保的物流运输。
局限性
虽然节约里程法在优化运输路径方面具有一定的优势，但也存在一些局限性。例如，该方法只考虑了运输里程的 节约，而忽略了其他因素（如时间、服务质量等）对运输成本的影响。此外，在实际应用中，还需要考虑车辆的 载重和容量限制、道路状况、客户需求等多种因素，这也会增加该方法的复杂性和难度。
02 节约里程法实例一：物流 配送优化
01
节约里程法的时间复杂度主要取决于需求点的数量和合并运输的次数。
02
在需求点数量较多的情况下，算法可能需要较长的时间来寻找最优解。
03
为了优化算法，可以考虑采用启发式搜索策略，如贪婪算法、遗传算 法等，来加快搜索速度并提高解的质量。
04
此外，还可以考虑对需求点进行聚类处理，以减少合并运输的次数和 降低算法复杂度。
节约里程法在路线规划中应用
景点间距离与交通方式选择
节约里程法
"节约里程法"节约里程法是用来解决运输车辆数目不确定的问题的最有名的启发式算法。
又称节约算法或节约法，可以用并行方式和串行方式来优化行车距离。
核心思想节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
基本规定利用节约法确定配送路线的主要出发点是，根据配送中心的运输能力和配送中心到各个用户以及各个用户之间的距离来制定使总的车辆运输的吨公里数最小的配送方案。
另还需满足以下条件；（1）所有用户的要求；（2）不使任何一辆车超载；（3）每辆车每天的总运行时间或行驶里程不超过规定的上限；（4）用户到货时间要求。
基本思想为达到高效率的配送，使配送的时间最小距离最短成本最低，而寻找的最佳配送路线。
计算公式计算方法如下图，假设O点为配送中心，它分别向地点A和B送货。
设O点到地点A和地点B的距离分别为a和b。
地点A和地点B之间的距离为c,现有两种运输方案,如图下(a)和(b)所示。
图(a) 两个地点单独运输计算公式图a图(b)两个地点合成一个回路进行运输计算公式图b容易得到：在上图(a)中运输距离为2(a+b)；图上(b)中运输距离为a+b+c；合并后的总运输距离之差为：2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c即得到计算公式是两点到中心的距离和减去两点间距离。
典型例题例题：已知配送中心P0向5个用户Pj配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如图1所示，配送中心有3台2t卡车和2台4t两种车辆可供使用。
利用节约里程法制定最优的配送方案。
第一步，作运输里程表，列出配送中心到用户及用户间的最短距离。
第二步，按节约里程公式求得相应的节约里程数。
第三步，将节约里程按从大到小顺序排列。
第四步，根据载重量约束与节约里程大小，顺序连接各客户结点，形成两个配送线。
节约里程法
工作人员的意见 各配送路线的负荷量尽量调整平衡 要充分考虑道路交道运输状况 预测需求的变化及发展 考虑等候时间
配送路线的选择
要考虑到司机的休息时间及指定的交货时间 由于交通状况及需求状况变化的影响，最好
利用仿真模拟研究对策
配送案例分析
已知配送中心(P0)向5个客户(P1~P5)配送 货物,其配送路线网络、配送中心与客户的 距离以及客户之间的距离（如图所示）图中 括号内的数字表示客户的需求量（单位： 吨），线路上的数字表示两节点之间的距离， 配送中线有3台2吨卡车和2台4吨两种车辆 可供使用。
组 合
EG FG
EF
DF CD BC DG CF
DE BD
E
FGE G
节
约 里
40 39 38 17 14 12
8
7
7
2
0
--- -
程
1)EG节约里程最大，它们的配送货物量 是:1.75+1.15=2.9T，在货车载重限度内，可以入选。
2)FG的配送货物量1.1T，正好可以与2.9T拼装为一辆4T 货车的载运量，它们相互衔接成为一条配送路线AEGFA。 全程为20＋1＋6＋24＝51KM。
连接点
f—g g—h h—i a—d b—i f—h b—e d—f g—i c—j e—g f—i
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
修正初始方案：按节约里程大小顺序，组成配送线路。
（0.4） 5
D
8
E
8
（0.8） 5
（1.5） B
4
C
线9 路1：运距
A
27km，4t车一
7
辆
10
配送路线的选择
要考虑到司机的休息时间及指定的交货时间 由于交通状况及需求状况变化的影响，最好
利用仿真模拟研究对策
配送案例分析
已知配送中心(P0)向5个客户(P1~P5)配送 货物,其配送路线网络、配送中心与客户的 距离以及客户之间的距离（如图所示）图中 括号内的数字表示客户的需求量（单位： 吨），线路上的数字表示两节点之间的距离， 配送中线有3台2吨卡车和2台4吨两种车辆 可供使用。
组 合
EG FG
EF
DF CD BC DG CF
DE BD
E
FGE G
节
约 里
40 39 38 17 14 12
8
7
7
2
0
--- -
程
1)EG节约里程最大，它们的配送货物量 是:1.75+1.15=2.9T，在货车载重限度内，可以入选。
2)FG的配送货物量1.1T，正好可以与2.9T拼装为一辆4T 货车的载运量，它们相互衔接成为一条配送路线AEGFA。 全程为20＋1＋6＋24＝51KM。
连接点
f—g g—h h—i a—d b—i f—h b—e d—f g—i c—j e—g f—i
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
修正初始方案：按节约里程大小顺序，组成配送线路。
（0.4） 5
D
8
E
8
（0.8） 5
（1.5） B
4
C
线9 路1：运距
A
27km，4t车一
7
辆
10
节约里程法
• 位势法
b
6
c
4
4
2
a
d
3
7 e
第三节 物流配送组织
• 分送式配送是指由一个供应点对多个客户的共同 送货。其基本条件是所有客户的需求量总和不大 于一辆车的额定载质量。送货时，由这一辆车装 着所有客户的货物，沿着一条精心选择的最佳线 路依次将货物送到各个客户手中，这样既保证按 时按量将用户需要的货物及时送到，又节约了文 辆，节省了费用，缓解了交通紧张的压力，并减 少了运输对环境造成的污染。
2—3：L2+L3-L23=8+17-10=15 2—4：L2+L4-L24=8+15-8=15 2—5：L2+L5-L25=8+15-9=14 2—6：L2+L6-L26=8+20-15=13 2—7：L2+L7-L27=8+17-13=12 2—8：L2+L8-L28=8+8-9=7 2—9：L2+L9-L29=8+6-12=2 2—10：L2+L10-L2、10=8+16-14=10 2—11：L2+L11-L2、11=8+21-18=11 2—12：L2+L12-L2、12=8+11-14=5 2—13：L2+L13-L2、13=8+15-20=3 3—4：L3+L4-L34=17+15-4=28 3—5：L3+L5-L35=17+15-14=18 3—6：L3+L6-L36=17+20-20=17
例：由配送中心P向A—I等9个用户配送货物。图中 连线上的数字表示公路里程（km）。靠近各用户 括号内的数字，表示各用户对货物的需求量（t）。 配送中心备有2t和4t载重量的汽车，且汽车一次 巡回走行里程不能超过35km，设送到时间均符合 用户要求，求该配送中心的最优送货方案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章层次分析法在苏北菜鸟物流中心选址上的应用4.1 层次分析法AHP 是由美国著名运筹学家、匹兹堡大学教授 T.L.Saaty 于二十世纪创立的，它是一种强有力的系统分析+运筹学方法，对多因素、多标准、多方案的综合评价及趋势预测相当有效。
面对由“方案层+因素层+目标层”构成的递阶层次结构决策分析问题，给出了一整套处理方法与过程。
AHP 最大的优点是可以处理定性和定量相结合的问题，可以将决策者的主观判断与政策经验导入模型，并加以量化处理，AHP 从本质上讲是一种科学的思维方式。
其主要的特点是：（1）面对具有层次结构的整体问题综合评价，采取逐层分解，变为多哥单准则评价问题，在多个单准则评价的基础上进行综合；（2）为解决定性因素的处理及可比性问题，Saaty 建议：以“重要性”（数学表现为 21权值）比较作为统一的处理格式.并将比较结果按重要程度以 1 至 9 级进行量化标度；（3）检验与调整比较链上的传递性，即检验一致性的可接受程度；（4）对汇集全部比较信息的矩阵集，使用线性代数理论与方法加以处理.挖掘出深层次的、实质性的综合信息作为决策支持。
当然层次分析法也是有其局限性的，具体表现在：（1）AHP 方法也有致命的缺点，它只能在给定的策略中去选择最优的，而不能给出新的策略；（2）AHP 方法中所用的指标体系需要有专家系统的支持，如果给出的指标不合理则得到的结果也就不准确；（3）AHP 方法中进行多层比较的时候需要给出一致性比较，如果不满足一致性指标要求，则AHP 方法方法就失去了作用；（4）AHP 方法需要求矩阵的特征值，但是在 AHP 方法中一般用的是求平均值（可以算术、几何、协调平均）的方法来求特征值，这对于一些病态矩阵是有系统误差的。
4.2 层次分析法的基本原理和步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模，大体上可按下面四个步骤进行：（1）建立递阶层次结构模型；（2）构造出各层次中的所有判断矩阵；（3）层次单排序及一致性检验；（4）层次总排序及一致性检验。
4.3 层次分析法实例应用4.3.1构造递阶层次结构模型根据苏北菜鸟物流中心选址影响因素的分析，菜鸟物流要在苏北淮安、徐州、连云港、宿迁、盐城这5个地方选择综合指标最好的地点作为物流中心建设地点，需要对这5个候选地的各项因素进行综合评价。
评判标准如下：（1）自然环境因素：越好则越有利于建造物流中心；（2）经营环境因素：越好则越有利于建造物流中心；（3）基础设施情况：越好则越有利于建造物流中心；（4）其他因素：越好则越有利于建造物流中心。
物流中心选址综合评价指标体系自然因素经营环境基础设施其他因素气候条件地质条件水文条件地形条件商品特征经营环境物流费用服务水平环境保护国土资源公共设施交通条件物流中心综合评价指标体系对这五个城市进行定性分析发现，连云港、盐城这两个城市位于苏北地区东部，地理位置较为偏僻。
而且这两个城市交通条件也与徐州、淮安、宿迁有一定差距。
其他物流公司也没有在连云港、盐城两个城市建立过苏北区的物流中心的例子。
因此，用定性分析便把这两个城市排除，最后再用层次分析法对徐州、淮安、宿迁三个城市进行分析计算。
选址G自然环境C 1经营环境C 2基础设施C 3其他因素C 4宿迁A 1徐州A 2淮安A 3利用层次分析法进行分析求出 宿迁、徐州、淮安这三个候选地适合程度的排序情况，在这里宿迁、徐州、淮安是我们要分析的决策变量，特别地，专家分析的自然环境因素和经营环境因素次层的变量重要程度相等，也就是说两两之比都为1。
为此，我们是把基础设施情况和其他因素的次层因素纳入分析范围。
表4-1 层次分析法判断标度标度 定义 简要说明1 同等重要 i 因素与j 因素同等重要 3 稍微重要 i 因素比j 因素略重要 5 较强重要 i 因素比j 因素较重要 7 强烈重要 i 因素比j 因素非常重要 9 绝对重要 i 因素比j 因素绝对重要2、4、6、8 上述两判断级的中间值为以上判断之间的中间状态对应的标度值 倒数反比较若i 因素与j 因素比较，得到判断值为，ji a =1/ ij a ，ii a =14.3.2构造各层次中的所有判断矩阵：先以第一层要素（选址层）为依据，对第二层（准则层）要素建立判断矩阵如下表所示。
表4-2 以选址层为依据对准则层要素建立判断矩阵表选址G C1C2C3C4优先级向量自然因素B1 1 8 5 3 0.567经营环境B2 1/8 1 1/2 1/6 0.056基础设施B3 1/5 2 1 1/3 0.104其他因素B4 1/3 6 3 1 0.273再以第二层要素（准则层）为依据，对第三层（方案层）要素建立判断矩阵。
由于此时有4个准则，故有4个判断矩阵，如下表所示。
表4-3 以自然因素为依据对各城市建立判断矩阵表自然因素C1A1A2A3优先级向量A1宿迁 1 1/3 1/9 0.068A2徐州 3 1 1/8 0.146A3淮安9 8 1 0.786表4-4 以经营环境为依据对各城市建立判断矩阵表自然因素C2A1A2A3优先级向量A1宿迁 1 3 9 0.640A2徐州1/3 1 8 0.306A3淮安1/9 1/8 1 0.054表4-5 以基础设施为依据对各城市建立判断矩阵表自然因素C3A1A2A3优先级向量A1宿迁 1 2 9 0.595A2徐州1/2 1 7 0.347A3淮安1/9 1/7 1 0.058表4-6 以其他因素为依据对各城市建立判断矩阵自然因素C4A1A2A3优先级向量A1宿迁 1 1/3 1/9 0.069A2徐州 3 1 1/7 0.155A3淮安9 7 1 0.7764.3.3层次单排序及其一致性检验)0(273.0104.0056.0567.0092.1418.0224.0266.2222.0316.0353.0201.0074.0105.0118.0121.0037.0053.0059.0075.0667.0526.0470.0603.01363131125161211813581WA =⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧−−−→−⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧−−−−→−⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧−−−−−−→−⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=归一化按行求和列向量归一化()T AW 273.0,104.0,056.0,567.0073.4273.0110.1104.0422.0056.0225.0567.0354.241110.1422.0225.0354.2273.0104.0056.0567.01363131125161211813581)0(max )0()0(==⎪⎭⎫⎝⎛+++=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=ωλ同理可计算出判断矩阵⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=179711391311171917121921,181918131931,1898113913114321B B B B ，对应的最大特征值与特征向量依次为：.776.0155.0069.0,083.3;058.0347.0595.0,024.3;054.0306.0640.0,216.3;786.0146.0068.0,111.34)1(max )4(3)1(max )3(2)1(max )2(1)1(max )1(⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==ωλωλωλωλ()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==776.0058.0054.0786.0155.0347.0306.0146.0069.0595.0640.0068.0,,,4)1(3)1(2)1(1)1()1(ωωωωω⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==667.0178.0155.0273.0104.0056.0567.0776.0058.0054.0786.0155.0347.0306.0146.0069.0595.0640.0068.0)0()1(ωωω用一致性指标进行检验：max 1nCI n λ-=-，RI CI CR =n 1 2 34 567 8 9 10 11RI0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51（1）对于判断矩阵A ，λ(0)max=4.073，RI=0.901.0027.090.0024.0024.0144073.4<====--=RI CI CR CI 表示A 的不一致程度在容许范围内，此时可用A 的特征向量代替权向量。
（2）同理，对于判断矩阵B1，B2，B3，B4利用上述原理均通过一致性检验。
4.3.4层次总排序及其一致性检验决策结果：是首选方案A3，其次是方案A2，再次是方案A1. 故选淮安作为苏北菜鸟物流中心。