节约里程法详解图
- 格式：doc
- 大小：121.50 KB
- 文档页数：6
下载文档原格式
合集下载
物流工程——节约里程法
物流配送——节约里程法(Saving Algorithm)
• 车辆调度程序法(Vehicle Scheduling Program:VSP) • 又称节约算法，是指用来解决运输车辆数目不确定的问题 的最有名的启发式算法。 核心思想: • 节约里程法核心思想是依次将运输问题中的两个回路合并 为一个回路，每次使合并后的总运输距离减小的幅度最大， 直到达到一辆车的装载限制时，再进行下一辆车的优化。 优化过程分为并行方式和串行方式两种。
（0.9）
P3
4
P2
以此类推，如果前面涉及了某些 路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
（1.7）
5
6 8
（1.4）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
5
（0.9）
P3
4
P2
（1.7）
配送线路1
（1.4）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
案例： • 宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见 下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优 化方法。公司客户分布在全国各地,这里主要以广东省内7家客户 及省外一家特殊客户的一次配送为例。
客户(i) 货运量 (qi) 东莞 江门 4.3 1.8 惠州 0.7 阳江 2.2 汕尾 3.6 揭阳 3.6 汕头 1.6 漳州 2
（2.4）
节约里程法
（0.9）
P3
（1.7）
P2
6 8
（1.4）
• 车辆调度程序法(Vehicle Scheduling Program:VSP) • 又称节约算法，是指用来解决运输车辆数目不确定的问题 的最有名的启发式算法。 核心思想: • 节约里程法核心思想是依次将运输问题中的两个回路合并 为一个回路，每次使合并后的总运输距离减小的幅度最大， 直到达到一辆车的装载限制时，再进行下一辆车的优化。 优化过程分为并行方式和串行方式两种。
（0.9）
P3
4
P2
以此类推，如果前面涉及了某些 路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
（1.7）
5
6 8
（1.4）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
5
（0.9）
P3
4
P2
（1.7）
配送线路1
（1.4）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
案例： • 宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见 下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优 化方法。公司客户分布在全国各地,这里主要以广东省内7家客户 及省外一家特殊客户的一次配送为例。
客户(i) 货运量 (qi) 东莞 江门 4.3 1.8 惠州 0.7 阳江 2.2 汕尾 3.6 揭阳 3.6 汕头 1.6 漳州 2
（2.4）
节约里程法
（0.9）
P3
（1.7）
P2
6 8
（1.4）
节约里程法PPT课件
的使用率和周转率。
实施效果
通过节约里程法的应用，共享单 车的调度系统得到了优化，高峰 时段的供不应求问题得到了缓解， 提高了共享单车的服务质量和用
户体验。
06
总结与展望
总结节约里程法的原理与应用
要点一
总结
要点二
应用
节约里程法的原理是基于车辆运输路径优化，通过合理安 排车辆行驶路线，减少车辆空驶和重复行驶的距离，达到 降低运输成本和提高运输效率的目的。在实际应用中，该 方法广泛应用于物流配送、公共交通和共享出行等领域。
节约里程法的应用场景
物流配送路线规划
总结词
节约里程法在物流配送路线规划中，能够优化车辆行驶路径，减少运输成本和 时间。
详细描述
通过计算各需求点之间的距离节约量，选择最佳的配送路线，使得车辆在满足 客户需求的同时，总行驶距离最短，从而达到节约成本和时间的目的。
公共交通路线规划
总结词
节约里程法在公共交通路线规划中， 能够提高线路效率和乘客出行体验。
里程法更注重求解的稳定性。
05
节约里程法的实际案例分 析
某快递公司的配送路线优化
01
02
03
背景介绍
某快递公司面临配送路线 不优化、成本高昂的问题， 需要采用节约里程法进行 配送路线的优化。
解决方案
利用节约里程法，对快递 公司的配送路线进行重新 规划，减少重复行驶和空 驶，提高车辆装载率。
实施效果
低运输成本。
它主要应用于多个发货点之间， 通过合并多个货物装载在同一辆
车上，实现运输效率最大化。
节约里程法的基本思想是通过优 化运输路线，减少车辆空驶和重 复行驶，提高运输效率，降低运
输成本。
适用范围与条件
实施效果
通过节约里程法的应用，共享单 车的调度系统得到了优化，高峰 时段的供不应求问题得到了缓解， 提高了共享单车的服务质量和用
户体验。
06
总结与展望
总结节约里程法的原理与应用
要点一
总结
要点二
应用
节约里程法的原理是基于车辆运输路径优化，通过合理安 排车辆行驶路线，减少车辆空驶和重复行驶的距离，达到 降低运输成本和提高运输效率的目的。在实际应用中，该 方法广泛应用于物流配送、公共交通和共享出行等领域。
节约里程法的应用场景
物流配送路线规划
总结词
节约里程法在物流配送路线规划中，能够优化车辆行驶路径，减少运输成本和 时间。
详细描述
通过计算各需求点之间的距离节约量，选择最佳的配送路线，使得车辆在满足 客户需求的同时，总行驶距离最短，从而达到节约成本和时间的目的。
公共交通路线规划
总结词
节约里程法在公共交通路线规划中， 能够提高线路效率和乘客出行体验。
里程法更注重求解的稳定性。
05
节约里程法的实际案例分 析
某快递公司的配送路线优化
01
02
03
背景介绍
某快递公司面临配送路线 不优化、成本高昂的问题， 需要采用节约里程法进行 配送路线的优化。
解决方案
利用节约里程法，对快递 公司的配送路线进行重新 规划，减少重复行驶和空 驶，提高车辆装载率。
实施效果
低运输成本。
它主要应用于多个发货点之间， 通过合并多个货物装载在同一辆
车上，实现运输效率最大化。
节约里程法的基本思想是通过优 化运输路线，减少车辆空驶和重 复行驶，提高运输效率，降低运
输成本。
适用范围与条件
劳动部物流师2级节约里程法
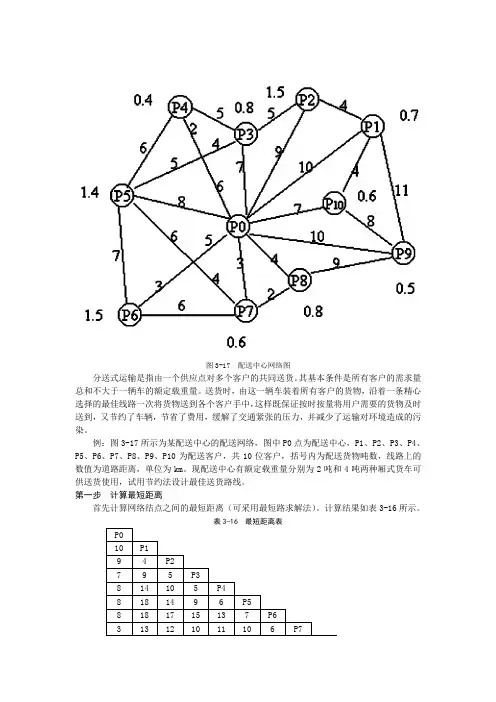
图3-17 配送中心网络图分送式运输是指由一个供应点对多个客户的共同送货。
其基本条件是所有客户的需求量总和不大于一辆车的额定载重量。
送货时，由这一辆车装着所有客户的货物，沿着一条精心选择的最佳线路一次将货物送到各个客户手中，这样既保证按时按量将用户需要的货物及时送到，又节约了车辆，节省了费用，缓解了交通紧张的压力，并减少了运输对环境造成的污染。
例：图3-17所示为某配送中心的配送网络，图中P0点为配送中心，P1、P2、P3、P4、P5、P6、P7、P8、P9、P10为配送客户，共10位客户，括号内为配送货物吨数，线路上的数值为道路距离，单位为km。
现配送中心有额定载重量分别为2吨和4吨两种厢式货车可供送货使用，试用节约法设计最佳送货路线。
第一步计算最短距离首先计算网络结点之间的最短距离（可采用最短路求解法）。
计算结果如表3-16所示。
表3-16 最短距离表第二步计算节约里程根据最短距离结果，计算出各客户之间的节约行程，结果见表3-17所示。
表3-17 节约里程表第三步将节约里程进行分类对节约行程按从大到小的顺序排列，如表3-18所示。
表3-18 节约里程排序第四步确定配送线路按节约里程大小顺序，组成线路图。
1、初始方案：如图3-18所示，从配送中心P0分别向各个客户进行配送，对每一客户分别单独派车送货，共有10条配送线路，总行程为148公里，需2吨货车10辆。
2、修正方案1：图3-18 图3-19按照节约行程的由大到小的顺序，连接P1和P2，P1和P10，P2和P3，P3和P4，形成巡回路线P0-P10-P1-P2-P3-P4-P0的配送线路，如图所示，装载货物4吨，这时配送路线总运行距离为109公里，配送线路6条，需4吨货车1辆，需2吨货车5辆，如图3-19所示。
3、修正方案2：按节约里程由大到小的顺序，连接P5和P6，P6和P7，形成巡回路线P0-P5-P6-P7-P0的配送线路，如图所示，装载货物3.5吨，这时配送路线总运行距离为85公里，配送线路4条，需4吨货车2辆， 图3-20 需2吨货车2辆，如图3-20所示。
节约里程法
算例：节约里程法以上一个二维码扫描算法算例为例，用节约里程法计算配送线路的安排。
解：① 首先根据上一个二维码扫描算法算例中的距离矩阵表计算出各点间的节约值矩阵表，如表1所示。
表1 节约值矩阵表② 从表1中选出节约值最大值为23，其对应的两个顶点为5、6。
5、6两处的需求量之和为8，未超过一辆车的运输能力14，因此，连接5、6成回路，即0—5—6—0。
再将顶点5与6的节约值赋为0，结果如表2所示。
表2 节约矩阵表计算过程1③ 从表2中再选出节约值最大值为20，其对应的两个顶点为7、8。
7、8两处的需求量之和为7，未超过一辆车的运输能力14，因此，连接7、8成回路，即0—7—8—0。
再将顶点7与8的节约值赋为0，结果如表3所示。
表3 节约矩阵表计算过程2④ 从表3中再选出节约值最大值为16，其对应的两个顶点为5、8或6、8。
如果连接5与8，则上述两条回路合并，其总需求量为15，超过一辆车的运输能力14，因此，5与8不能连接，同样6和8也不能连接，则将顶点5、8和6、8的节约值赋为0，结果如表4所示。
表4 节约矩阵表计算过程3⑤ 从表4中再选出节约值最大值为15，其对应的两个顶点为4、6。
如连接4与6，则形成：0—5—6—4—0回路，其总需求量为11，未超过一辆车的运输能力14，因此，连接4、6成新回路，即0—5—6—4—0。
再将顶点4与6的节约值赋为0，同时，由于顶点6成为回路的中间点，则与顶点6相关的节约值都赋为0。
表示顶点6不可能再与其他点相连，其结果如表5所示。
表5-33 节约矩阵表计算过程4⑥ 按算法步骤迭代运算，直到节约值矩阵表中的值均为0时，迭代结束。
最终的结果为：0—2—3—0，0—5—6—4—0，0—7—8—1—0这三条线路，其运输量分别为9、11、13，总里程数为93。
一般来说，节约里程法可以得到比较好的结果，但此算法也是一种贪婪启发式算法，对于一些特殊的算例，得不到最优解。
上一个二维码中算例的全局最优解是：选择0—1—3—0，0—2—7—8—0，0—5—6—4—0这三条线路，其运输量分别为11、11、11，总里程数为90。
节约里程法
定义节约里程法又称节约算法或节约法，是指用来解决运输车辆数目不确定的问题的最有名的启发式算法。
[1]2核心思想节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
[1]3基本规定利用节约法确定配送路线的主要出发点是，根据配送中心的运输能力和配送中心到各个用户以及各个用户之间的距离来制定使总的车辆运输的吨公里数最小的配送方案。
另还需满足以下条件；（1）所有用户的要求；（2）不使任何一辆车超载；（3）每辆车每天的总运行时间或行驶里程不超过规定的上限；（4）用户到货时间要求。
[2]4基本思想为达到高效率的配送，使配送的时间最小距离最短成本最低，而寻找的最佳配送路线。
[2]5典型例题例题：已知配送中心P0向5个用户Pj配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图所示，配送中心有3台2t卡车和2台4t两种车辆可供使用。
利用节约里程法制定最优的配送方案。
[1]节约里程法例题用图第一步，作运输里程表，列出配送中心到用户及用户建的最短距离。
[1]第二步，按节约里程公式求得相应的节约里程数。
[1]第三步，将节约里程按从大到小顺序排列。
[1]第四步，根据载重量约束与节约里程大小，顺序连接各客户结点，形成两个配送线。
[1]P2P3－P3P4－P2P4－P4P5－P1P2－P1P5－P1P3－P2P5－P3P5－P1P4得出结果：配送线路一：运量=1.7+0.9+1.4=4t运行距离=8+4+5+7=24km用一辆4t车运送，节约距离为18km 配送线路二：运量=2.4+1.5=3.9t<4t运行距离=8+10+16=34km用一辆4t车运送，节约距离为2km[1]初始方案：配送线路5条，需要车5辆，配送距离=39*2=78km 优化后的方案：2条配送路线,2辆4t车，配送距离=24+34=78km[1]。
节约里程法ppt课件
G
H
I
J
表2 最短距离表
第二步：由最短距离表，利用“节约里程”法计算出各连锁分店之间 的节约里程，做出节约里程表（见表3），计算结果有正有负，节约里 程为负数时，无实际意义，在表内写0。
表3 节约里程表
A A B C D E F G H I J
B
C
D
E
F
G
H
I
J
第三步：将节约里程由大到小顺序排列，列出节约里程排序表（见表 4），以便尽量使节约里程最多的点组合装车配送。
配送线路的优化
一、配送线路的优化方法 ㈡一对多配送的最短路线问题
节约里程法
原理：三角形一边之长必定小于另外两边之和。
A
L1 配 送 中 心 用 户 L1 配 送 中 心 L3
A
用 户
P
L2 往 返 发 货
P
L2 巡 回 发 货
B
用 户
B
用 户
在汽车载重量允许的情况下，采用巡回发货比采用往返发货可节约汽车走行 里程为：∆L=[2(L1+L2)]-(L1+L2+L3)=L1+L2-L3
• （1）初始方案：对每一客户分别单独派车 送货，结果如图11-10。
• 修正方案4
第四节
配送路线设计
一、配送路线选择问题
物流中心在组织货物配送时，有n个客户，处在同一城市不同地区，如 何取定最佳的配送路线？
例题：如图8-1所示的运输网络，试求出最优路线。
V1 10 V
3
10
V
6
V1
10
V310来自第一步：计算最短距离。根据配送网络中的已知条件， 计算配送中心与客户及客户之间的最短距离，结果见表 11-11。 第二步：计算节约里程sij,结果见表11-12。
配送路线优化(里程节约法)
5
P4
P5 2.4 10 16 18 16 12 P5
节约里程法
第2步：按节约里程公式求得相应的节约里程数
需求量 P0
1.5 8
P1
12 1.7 8
4
13 0.9 6
1
15 1.4 7
0
16 2.4 10
2
P2
4
10
P3
9
5
6
8
P4
18
16
12
0
0
5
P5
节约里程法
第 3 步：将节约里程按从大到小顺序排列
（0.9）
P3
4
（1.7）
P2
5
6
8
（1.4）
P4
7
P0
10
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
P1 (1.5)
节约里程法 （0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
P1 (1.5)
请为百家姓配送中心制定最优的配送方案。
第一步：计算最短距离。根据配送网络中的已知条件， 计算配送中心与客户及客户之间的最短距离，结果见表 11-11。 第二步：计算节约里程sij,结果见表11-12。
第三步：将节约sij,进行分类，按从大到小的顺序排 列，得表11-13
节约里程法
b94b
c795c
d 8 14 10 5 d
e 8 18 14 9 6 e
f 8 18 17 15 13 7 f
g 3 13 12 10 11 10 6 g
h 4 14 13 11 12 12 8 2 h
i 10 11 15 17 18 18 17 11 9 i
ห้องสมุดไป่ตู้
j 7 4 8 13 15 15 15 10 11 8 j
5
5
d
c
b4
6
a
e
4
7 8
7 Q
j
f
3
10
g
h
2
9
i
最佳配送线路
8
配送线路的优化
节约里程法 1、节约里程的基本原理
用一辆车将所有客户的货物装在一起，沿着一条精心 选择的最佳路线，将货物送到客户手中。 目标：节约车辆、节约费用、缓解交通压力、减少环 境污染。
△S = S1 + S2 - S3
1
2、按节约里程法制定配送计划 例 有一配送中心（Q）要向10个用户配送，配送距离 （公里）和需用量（吨）如下图所示。 假设：采用最大载重量2吨、4吨、8吨三种汽车，并限 定车辆一次运行距离50公里。 用节约里程法选择最佳配送路线和车辆的调度。
j 13 8 1 0 0 0 0 0 9
节约里程计算过程
5
第四步：将节约里程按大小顺序排列分类。
节约里程顺序表
分类 Ⅰ
用户连接 线
a—b
节约里 程
15
分类 Ⅸ
用户连接 线
f—g
Ⅱ
a—j
13
Ⅸ
g—h
Ⅲ
b—c
11
物流管理《8节约里程法及举例(郑克俊2019.11.30修订)》
节约里程法及举例1当由一个配送中心向多个客户进行共同送货，在一条线路上的所有客户的需求量总和不大于一辆车的额定载重量时，由这一辆车配装着所有客户需求的货物，按照一条预先设计好的最正确路线依次将货物送到每一客户手中，这样既可保证按需将货物及时送交，同时又能节约行驶里程，缩短整个送货时间，节约费用。
节约里程法正是用来解决这类问题的较成熟的方法。
用节约里程法确定配送路线的主要思路是，根据配送中心的运输能力及其到各客户之间的距离和各客户之间的相对距离，来制定使总的配送车辆吨公里数到达或接近最小的配送方案。
节约里程法的根本思路如下图，P 为配送中心所在地，A 和B 为客户所在地，相互之间道路距离分别为a 、b 、c 。
最简单的配送方法是利用两辆车分别为A 、B 客户配送，此时，如图〔b 〕所示，车辆运行距离为2a 2b 。
然而，如果按图〔c 〕所示改用一辆车巡回配送，运行距离为abc 。
如果道路没有什么特殊情况，可以节省的车辆运行距离为2a 2b –abc =ab –c >0，这个节约量“ab –c 〞被称为“节约里程〞。
AAABPPPB（a ）物流网络（c ）用一辆车配送ac ba cb ab c图 配送中心配送路线的选择1郑克俊仓储与配送管理〔第四版〕科学出版社 修订。
步骤：实际上如果给数十家、数百家客户配送，〔1〕应首先计算包括配送中心在内的相互之间的最短距离，〔2〕然后计算各客户之间的可节约的运行距离，〔3〕按照节约运行距离的大小顺序连结各配送地并设计出配送路线。
下面举例说明节约里程法的求解过程。
例节约里程法举例图为某配送网络，P为配送中心所在地，A～J为客户所在地，共10个客户，括号内的数字为配送量〔单位：吨〕，路线上的数字为道路距离〔单位：千米〕。
现有可以利用的车辆是最大装载量为2吨和4吨的两种厢式货车，并限制车辆一次运行距离在30千米以内。
为了尽量缩短车辆运行距离，试用节约里程法设计出最正确配送路线。
节约里程法
=27+34=61(Km) 节约费用:C=(61/25)×45=109.8（元）
7
12 5
P5 （2.5） 9
（1.7） P2
4 8
P1 （2.8）
P0 19
11
（1.6）
P7 （1.8）
配送线路： ①P0→P2→P3→P4→P0（27Km）,派4t车1辆 ②P0→P5→P6→P7→P0(44Km),派6t车1辆 ③P0→P1→P0(16Km),派4t车1辆 节约里程数:△S=148－(27+44+16)=61(Km)
设配送中心P0向7个用户Pj配送货物，其配送路线网 络、配送中心与用户的距离以及用户之间的距离如下图1
与下表1所示，图中括号内的数字表示客户的需求量( 单位：t)，线路上的数字表示两结点之间的距离(单位 ：km)，现配送中心有2台4t卡车和2台6t卡车两种车辆 可供使用。
⑴试用节约里程法制定最优的配送方案。
O 图2
△L=L1－L2=2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c
2.节约里程法核心思想
节约里程法核心思想是依次将运输问题中的两个回路 合并为一个回路，每次使合并后的总运输距离减小的幅 度最大，直到达到一辆车的装载限制时，再进行下一辆 车的优化。
3.节约里程法的应用
⑵设配送中心在向用户配送货物过程中单位时间平均支 出成本为45元，假定卡车行驶的平均速度为25公里/ 小时，试比较优化后的方案比单独向各用户分送可节 约多少费用？
（0.8t）
P3
（1.7t） 4
5
P2
7
11
4
（1.4t）P4
12
10
7
12 5
P5 （2.5） 9
（1.7） P2
4 8
P1 （2.8）
P0 19
11
（1.6）
P7 （1.8）
配送线路： ①P0→P2→P3→P4→P0（27Km）,派4t车1辆 ②P0→P5→P6→P7→P0(44Km),派6t车1辆 ③P0→P1→P0(16Km),派4t车1辆 节约里程数:△S=148－(27+44+16)=61(Km)
设配送中心P0向7个用户Pj配送货物，其配送路线网 络、配送中心与用户的距离以及用户之间的距离如下图1
与下表1所示，图中括号内的数字表示客户的需求量( 单位：t)，线路上的数字表示两结点之间的距离(单位 ：km)，现配送中心有2台4t卡车和2台6t卡车两种车辆 可供使用。
⑴试用节约里程法制定最优的配送方案。
O 图2
△L=L1－L2=2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c
2.节约里程法核心思想
节约里程法核心思想是依次将运输问题中的两个回路 合并为一个回路，每次使合并后的总运输距离减小的幅 度最大，直到达到一辆车的装载限制时，再进行下一辆 车的优化。
3.节约里程法的应用
⑵设配送中心在向用户配送货物过程中单位时间平均支 出成本为45元，假定卡车行驶的平均速度为25公里/ 小时，试比较优化后的方案比单独向各用户分送可节 约多少费用？
（0.8t）
P3
（1.7t） 4
5
P2
7
11
4
（1.4t）P4
12
10
节约里程法
工作人员的意见 各配送路线的负荷量尽量调整平衡 要充分考虑道路交道运输状况 预测需求的变化及发展 考虑等候时间
配送路线的选择
要考虑到司机的休息时间及指定的交货时间 由于交通状况及需求状况变化的影响，最好
利用仿真模拟研究对策
配送案例分析
已知配送中心(P0)向5个客户(P1~P5)配送 货物,其配送路线网络、配送中心与客户的 距离以及客户之间的距离（如图所示）图中 括号内的数字表示客户的需求量（单位： 吨），线路上的数字表示两节点之间的距离， 配送中线有3台2吨卡车和2台4吨两种车辆 可供使用。
组 合
EG FG
EF
DF CD BC DG CF
DE BD
E
FGE G
节
约 里
40 39 38 17 14 12
8
7
7
2
0
--- -
程
1)EG节约里程最大，它们的配送货物量 是:1.75+1.15=2.9T，在货车载重限度内，可以入选。
2)FG的配送货物量1.1T，正好可以与2.9T拼装为一辆4T 货车的载运量，它们相互衔接成为一条配送路线AEGFA。 全程为20＋1＋6＋24＝51KM。
连接点
f—g g—h h—i a—d b—i f—h b—e d—f g—i c—j e—g f—i
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
修正初始方案：按节约里程大小顺序，组成配送线路。
（0.4） 5
D
8
E
8
（0.8） 5
（1.5） B
4
C
线9 路1：运距
A
27km，4t车一
7
辆
10
配送路线的选择
要考虑到司机的休息时间及指定的交货时间 由于交通状况及需求状况变化的影响，最好
利用仿真模拟研究对策
配送案例分析
已知配送中心(P0)向5个客户(P1~P5)配送 货物,其配送路线网络、配送中心与客户的 距离以及客户之间的距离（如图所示）图中 括号内的数字表示客户的需求量（单位： 吨），线路上的数字表示两节点之间的距离， 配送中线有3台2吨卡车和2台4吨两种车辆 可供使用。
组 合
EG FG
EF
DF CD BC DG CF
DE BD
E
FGE G
节
约 里
40 39 38 17 14 12
8
7
7
2
0
--- -
程
1)EG节约里程最大，它们的配送货物量 是:1.75+1.15=2.9T，在货车载重限度内，可以入选。
2)FG的配送货物量1.1T，正好可以与2.9T拼装为一辆4T 货车的载运量，它们相互衔接成为一条配送路线AEGFA。 全程为20＋1＋6＋24＝51KM。
连接点
f—g g—h h—i a—d b—i f—h b—e d—f g—i c—j e—g f—i
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
修正初始方案：按节约里程大小顺序，组成配送线路。
（0.4） 5
D
8
E
8
（0.8） 5
（1.5） B
4
C
线9 路1：运距
A
27km，4t车一
7
辆
10
第九讲节约里程法案例详解
二、短期成本 (一)短期成本的分类 (二)各种短期成本的变动及其关系
（一）短期成本的分类 1.短期总成本 1.短期总成本 2.短期平均成本 2.短期平均成本 3.短期边际成本 3.短期边际成本
1.短期总成本 总成本：是企业生产某一产量的各项成本之和。 总成本：是企业生产某一产量的各项成本之和。 是企业生产某一产量的各项成本之和 STC=TFC+STVC
（5）分拣间接费用 分拣间接费用是指配送分拣管理部门为管理和组 织分拣作业，需要由分拣成本分担的各项管理费 用和业务费用。 分拣直接费用与间接费用就构成了配送环节的分 拣成本，即： 分拣成本=分拣直接费用+分拣间接费用
配装成本的计算 配装成本是指在完成配装货物过程中所发生 的各种费用之和。 （1）材料费：配装过程中消耗的各种材料，如 木材、包装纸、金属、塑料等。根据“材料发出 凭证汇总表”、“领料单”及“领料登记表”等 初始凭证，配装成本好用的金额计入成本。 （2）工资及职工福利费：工资是按规定支付给 装配作业职工的标准工资、奖金和津贴等。职工 福利费是按标准的工资总额和提取标准计提的职 工福利费。根据“工资分配汇总表”和“职工福 利费”中分配的配装成本的金额计入成本。
（二）配送成本的影响因素 配送成本是各种作业活动的费用，它的大小与下面的因素 有关： 1. 时间 配送时间持续的后果是占用了配送中心，耗用了配送 中心的固定成本。而这种成本往往表现为机会成本，使得 配送中心不能提供其他配送服务获得收入或者在其他配送 服务上增加成本 2. 距离 距离是构成配送运输成本的主要内容。距离越远，也 就意味着运输成本增高，同时造成运输设备增加，送货员 增加等。
1.配送运输费用 配送运输费用主要包括以下方面： （1）车辆费用。车辆费用指从事配送运输生产而发生的各 项费用。具体包括驾驶员及助手等工资及福利费、燃料、 轮胎、修理费、折旧费、养路费、车船使用税等项目。 （2）营运间接费用。这是指营运过程中发生的不能直接计 入各成本计算对象的站、队经费。包括站、队人员的工资 及福利费、办公费、水电费、折旧费等内容，但不包括管 理费用。
物流工程——节约里程法ppt课件
P2
8
8
P5
P1 (1.5)
配送线路1：
（2.4）
运量 = 1.7+0.9+1.4= 4t
运行距离＝8＋4＋5＋7＝24km
用一辆 4t车运送
节约距离 =18km（即2*21-24）
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 节约距离=2km（即2*18-34）
P2P3----P3P4-----P1P5
（1.7）
P2
5
6
8
（1.4）
P4
7
P0
10
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
练习题
某连锁零售店，下设有一个配送中心P和10个连 锁分店A～J，配送中心和各连锁分店及各连锁分店之 间的位置关系如下图1所示，两点间连线上的数字为 两点间的路线长度（单位：公里）。各连锁分店对某 种商品的需求量见表1，该商品由配送中心统一采购 并进行配送。配送中心备用2t和4t的货车，限定送货 车辆一次巡回距离不超过35公里，设送到时间均符合 用户要求，求配送中心的最优送货方案。
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
8
8
P5
P1 (1.5)
配送线路1：
（2.4）
运量 = 1.7+0.9+1.4= 4t
运行距离＝8＋4＋5＋7＝24km
用一辆 4t车运送
节约距离 =18km（即2*21-24）
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 节约距离=2km（即2*18-34）
P2P3----P3P4-----P1P5
（1.7）
P2
5
6
8
（1.4）
P4
7
P0
10
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
练习题
某连锁零售店，下设有一个配送中心P和10个连 锁分店A～J，配送中心和各连锁分店及各连锁分店之 间的位置关系如下图1所示，两点间连线上的数字为 两点间的路线长度（单位：公里）。各连锁分店对某 种商品的需求量见表1，该商品由配送中心统一采购 并进行配送。配送中心备用2t和4t的货车，限定送货 车辆一次巡回距离不超过35公里，设送到时间均符合 用户要求，求配送中心的最优送货方案。
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法PPT课件
授课：XXX
35
配送线路的优化
（一）直送式配送：位势法 （二）分送式配送：节约里程法 1、节约里程的基本原理
用一辆车将所有客户的货物装在一起，沿着一条精心 选择的最佳路线，将货物送到客户手中。 目标：节约车辆、节约费用、缓解交通压力、减少环 境污染。
△S = S1 + S2 - S3
授课：XXX
36
送货，需要2t货车10辆，走行授总课里：X程XX148km。
14
案例分析
• 例 ： 某 一 配 送 中 心 p0 向 10 个 客 户 pj(j=1,2,…,10) 配 送 货 物 ， 其 配 送 网 络 如 图 11-9所示。图中括号内的数字表示客户的需 求量（T），线路上的数字表示两节点之间 的距离。配送中心有2t和4t两种车辆可供使 用，试制定最优的配送方案。
节约里程
顺序排位
15
13
13
13
11
13
10
16
10
16
9
16
9
19
9
19
8
21
8
22
7
22
6
22
授课：XXX
连接线
F－ G G－ H H－ I B－ I A－ D F－ H B－ E D－ F G－ I C－ J E－ G F－ I
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
13
第四步：根据节约里程排序表和配送车辆载重及行驶里程等约束条件，
第四步：确定配送线路。从分类表中，按节约里程大小顺序，组成线路图
授课：XXX
19
• （1）初始方案：对每一客户分别单独派车 送货，结果如图11-10。
节约里程法详解图
例：有一配送（P）具有如图所示的配送网络，其中A-J表示收货站，（）内数字表示发送量（吨），路线上的数字表示道路距离（公里）。
问为使行走距离尽量小，应该如何去求配送线路？假设能够利用的车是2吨车（即最大载重量是2吨）和4吨车两种，并限制车辆一次运行的初步距离是30公里。
解题步骤：1.第一步：作出最短距离矩阵，首先从配送网络图中计算出配送中心与收货点之间以及收货点相互之间的最短距离矩阵，见下表所示：表一：最短距离矩阵（单位：公里）例如：计算A-B的节约里程项目如下：P-A的距离是：a=10P-B的距离是：b=9A-B的距离是：c=4节约里程项目为：a+b-c=10+9-4=15公里3.第三步：节约项目分类，再把节约项目由大到小顺序排列。
（1）.初次解。
线路数：10总行走距离：(10+9+7+8+8+8+3+4+10+7)*2=148公里车辆台数：2吨车10台（2）.二次解。
按节约里程由大到小的顺序，连接A-B，A-J，B-C连接线。
线路数：7总行走距离：148-15-13-11=109公里车辆台数：2吨车6台，4吨车1台（3）.三次解。
其次节约里程最大的是C-D和D-E。
C-D，D-E两者都有可能与二次解的线路A连接，但由于A的车辆载重量与行走距离有限，不能再增加收货点。
为此，略去C-D而连接D-E。
总行走距离：109-10=99公里车辆台数：2吨车5台，4吨车1台（4）.四次解。
接下来节约里程大的是A-I和E-F。
由于A已组合在完成的线路A中，所以略去，不能再增加收货点。
为此，略去A-I 而将E-F连接在线路B上。
线路数：5总行走距离：99-9=90公里车辆台数：2吨车3台，4吨车2台（5）.五次解。
再继续按节约里程由大到小排出I-J，A-C，B-J，B-D，C-E。
由于同一组总有一头或两头包含在已完成的线路A中，不能再作出新的线路。
只考虑把下一组F-G组合在完成的线路B中。
总行走距离：85公里车辆台数：2吨车2台，4吨车2台线路A：4吨车，总行走距离27公里，装载量3.6吨。
第十四讲 节约里程法
第十四讲节约里程法学习目标●掌握配送线路优化的目标与约束条件●理解节约里程法的原理;●掌握节约里程法的运用步骤;●能运用节约里程法制订简单的配送线路方案;一、配送活动的七要素1、货物：指配送标的物的种类、形状、重量、包装、材质、装运要求等。
2、客户：指委托人、收货人3、车辆：指配送工具4、人员：指司机或配送业务员5、路线：指配送路线6、地点：指配送的起点和终点7、时间：不仅仅指在途时间，还包括装卸搬运时间。
二、配送线路优化选择1、配送线路优化选择的意义●配送路线：是指各送货车辆向各个用户送货时所要经过的路线。
●配送路线是否合理对配送速度、成本、效益影响很大。
●主要方法有：方案评价法、数学计算法和节约里程法等。
2、配送线路优化的目标●以效益最高为目标；●以成本最低为目标；●以路程最短为目标；●以吨公里数最小为目标；●以准确性最高为目标；●运力利用最合理、劳动消耗最低为目标。
3、配送路线优化选择的约束条件●满足所有收货人对货物品种、规格、数量的要求；●满足收货人对货物送达时间范围的要求；●在允许通行的时间段内进行配送；●各配送路线的货物量不得超过车辆空间和载重量的限制；●在配送中心现有运力允许的范围内。
三、节约里程法1、节约里程法的概念节约里程法（Saving Algorithm）又叫节约算法，是用来解决配送车辆数目不确定的VRP问题的最有名的启发式算法。
它的核心思想是依次将配送作业中的两个回路合并为一个回路，使得每次合并后的总运输距离减少的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
2、节约里程法的原理三角形两边之和大于第三边。
3、节约里程法的应用步骤步骤1：计算配送网络结点之间的最短距离。
步骤2：计算通过共同配送模式使得各客户之间的可节约的运行距离（a+b －c）。
其中，a、b分别为配送中心P到各用户的最短距离，c为两用户之间的最小距离。
步骤3：对节约里程数按大小顺序进行排列。
运输路线优化
将A、表B、：C和D连在一起，距离O—A—B—
C—D—O，超过了75千米，不予采纳。
选择另节一约个值最计大的算节表约值10，将B、C
和D连接在一起，距离O—B—C—D—O，
超过了75 千米，仍然不采纳。
选择另O一个A最大B的节C约值D5 ，将A、C
和大于D连A7接5千在—米一，起—不，采距纳2离0。O—5 A—5D—C—O，约值开第始二，步将：客从户最连大接的在节
LOGO
物流运输管理
运输线路的优化
（2）运输线路的选择 节约里程法 最短路径法
图表作业法 图上作业法
1．Байду номын сангаас约里程法
从仓库O要运送货物
外一种路线，从O到A
在车辆路线设给计客方户案A和中B ，“节约法”到 为B：是，a＋再最b到广＋Ox。为。总将人距客离
知的方法，它也形成了人工和计算机载荷户结计合划考系虑，统在的第二
表示两地的距离
500 c 45
300 C
小飞守角制作
步骤3：制定商品运输方案
a
300
B
200
D
50 A 75
80 b 95
700
400
70
800
600
0
200 400
60
600
500 c
300
45C
300
小飞守角制作
步骤4：填入商品平衡表
A
B
C
D 调入量
a
400 300
700
b
200
600 800
步骤2
找出与出发点相邻但未标号点的 最小距离值并在相应点标号。
找出与
已标号点相邻 但未标号点的 最小距离值并 在相应点标号 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例：有一配送（P）具有如图所示的配送网络，其中A-J表示收货站，（）内数字表示发送量（吨），路线上的数字表示道路距离（公里）。
问为使行走距离尽量小，应该如何去求配送线路？假设能够利用的车是2吨车（即最大载重量是2吨）和4吨车两种，并限制车辆一次运行的初步距离是30公里。
解题步骤：
1.第一步：作出最短距离矩阵，首先从配送网络图中计算出配送中心与收货点之间以及收货点相互之间的最短距离矩阵，见下表所示：
表一：最短距离矩阵（单位：公里）
例如：计算A-B的节约里程项目如下：
P-A的距离是：a=10
P-B的距离是：b=9
A-B的距离是：c=4
节约里程项目为：a+b-c=10+9-4=15公里
3.第三步：节约项目分类，再把节约项目由大到小顺序排列。
（1）.初次解。
线路数：10
总行走距离：(10+9+7+8+8+8+3+4+10+7)*2=148公里
车辆台数：2吨车10台
（2）.二次解。
按节约里程由大到小的顺序，连接A-B，A-J，B-C连接线。
线路数：7
总行走距离：148-15-13-11=109公里
车辆台数：2吨车6台，4吨车1台
（3）.三次解。
其次节约里程最大的是C-D和D-E。
C-D，D-E两者都有可能与二次解的线路A连接，但由于A的车辆载重量与行走距离有限，不能再增加收货点。
为此，略去C-D而连接D-E。
总行走距离：109-10=99公里
车辆台数：2吨车5台，4吨车1台
（4）.四次解。
接下来节约里程大的是A-I和E-F。
由于A已组合在完成的线路A中，所以略去，不能再增加收货点。
为此，略去A-I 而将E-F连接在线路B上。
线路数：5
总行走距离：99-9=90公里
车辆台数：2吨车3台，4吨车2台
（5）.五次解。
再继续按节约里程由大到小排出I-J，A-C，B-J，B-D，C-E。
由于同一组总有一头或两头包含在已完成的线路A中，不能再作出新的线路。
只考虑把下一组F-G组合在完成的线路B中。
总行走距离：85公里
车辆台数：2吨车2台，4吨车2台
线路A：4吨车，总行走距离27公里，装载量3.6吨。
线路B：4吨车，总行走距离30公里，装载量3.9吨。
线路C：2吨车，总行走距离23公里，装载量1.3吨。
这样整个配送线路做完，共3条线路总行走距离80公里，必要车辆是2吨车1台，4吨车2台。
采用节约里程法注意事项：
1.适用于需要稳定的顾客。
2.对于非固定需要的顾客，采用其它途径配车，或并入有宽裕的
线路中。
3.最终确定的配送线路，要有司机和现场意见。
4.挑战配送线路的负荷量使其平衡。
5.充分考虑道路交通情况。
6.考虑需要的变动。
7.考虑在收货站的停留的时间。
8.注意司机的休息时间和指定交货时间。
9.为找出交通情况和需要变化所造成的影响，研究采用模拟方式
的可能性。
10.车辆安排程序作为大部分计算机应用程序组已很完善，对规模
较大的网络，需要采用电子计算机处理。