有理数的加法(2)
- 格式:docx
- 大小:11.00 KB
- 文档页数:3
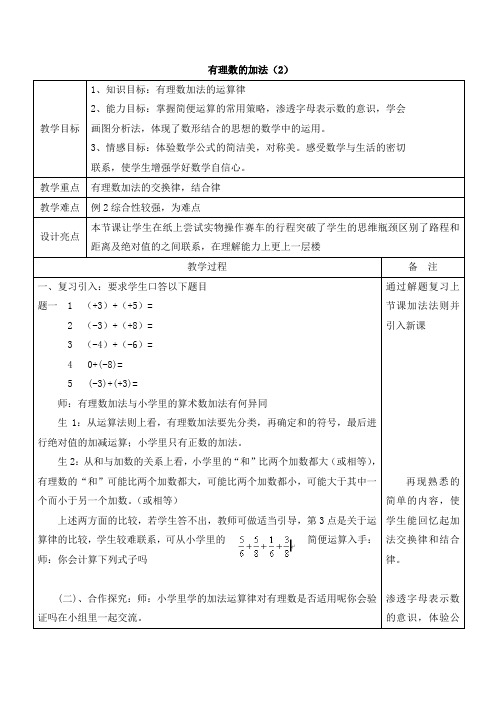
有理数的加法(2)一、复习引入:要求学生口答以下题目题一 1 (+3)+(+5)=2 (-3)+(+8)=3 (-4)+(-6)=4 0+(-8)=5 (-3)+(+3)=师:有理数加法与小学里的算术数加法有何异同生1:从运算法则上看,有理数加法要先分类,再确定和的符号,最后进行绝对值的加减运算;小学里只有正数的加法。
生2:从和与加数的关系上看,小学里的“和”比两个加数都大(或相等),有理数的“和”可能比两个加数都大,可能比两个加数都小,可能大于其中一个而小于另一个加数。
(或相等)上述两方面的比较,若学生答不出,教师可做适当引导,第3点是关于运算律的比较,学生较难联系,可从小学里的简便运算入手:师:你会计算下列式子吗(二)、合作探究:师:小学里学的加法运算律对有理数是否适用呢你会验证吗在小组里一起交流。
让小组代表发言,师板书:在有理数的运算中,加法交换律和结合律仍成立。
加法交换律:两个数相加,交换加数的位置,和不变 a+b=b+a加法结合律:三个数相加,先把前两个数相加,或则先把后两个数相加,和不变。
(a+b )+c=a+(b+c )例3、计算:(1) 15+(-13)+18;(2) (-2.48)+4.33+(-7.52)+(-4.33)(3) +(-)+(-)+(-)师生共同完成。
小结:1、任意若干个数相加,无论各数相加的先后次序如何,其和不变2、简便运算的常用策略:1、可以把正数或负数分别结合在一起相加2、有相反数的先把相反数相加3、能凑整的先凑整有分母相同的4、先把同分母的数相加 练一练:P 32 2、用简便方法计算,并说明有关理由: (1)(+14)+(-4)+(-1)+(+16)+(-5) (2)(-18.65)+(-7.25)+18.75+7.25(3)(-2.25)+(-)+(-)+0.125(4)(-3.5)+[3+(-1.5)]解决实际问题例4、小明遥控一辆玩具赛车,让它从A 地出发,先向东行驶15m ,再向西行驶25m ,然后又向东行驶20m ,再向西行驶35m ,问玩具赛车最后停在何处一共行驶了多少米师:这两问中,你有把握解决哪一问师:第一问包含几个意思 生:两个,要求方向和距离。




参考答案1. C【解析】这个运算中运用了加法的结合律和交换律.故选C.2. (-2)113【解析】将四个数中的同号两数组合即可,即(-7)+11+3+(-2)=[(-7)+(-2)]+(11+3).3. 解:(1)原式=[(-87)+37]+[42+(-22)]=(-50)+20=-30.(2)原式=[(-2.1)+5]+[3.35+(-3.35)]+[4.7+(-4.7)]=2.9+0+0=2.9.4. C【解析】(+128.5)+(-140)+(-95.5)+280=(128.5+280)+[(-140)+(-95.5)]= 408.5+(-235.5)=173.故选C.5. 东1【解析】(-4)+(+7)+(-9)+(+8)+(+6)+(-4)+(-3)=[(+7)+(+8)+(+6)]+[(-4)+(-9)+(-4)+(-3)]=21+(-20)=1(千米).故收工时在A地东边1千米处.6. 解:-6-3+5-1+7+2-3+4-3+3=21-16=5千克,这10袋小麦总计超过5千克;10×50+5=500+5=505(千克),10袋小麦总质量是505千克.7. C【解析】11+[(-13)+7]=11-6=5,故选项A错误;(-2.5)+[5+(-2.5)]=-2.5+2.5=0,故选项B错误;[312+(-312)]+(-2)=0-2=-2,故选项C正确;3.14+[(-4)+3.14]=3.14-0.86=2.28,故选项D错误.故选C.8. B【解析】根据绝对值的性质可知大于-2 019而小于2 018的所有整数是0,±1,±2,±3,…,±2 018,-2019,每一组绝对值相等的数均互为相反数,故大于-2 019小于2 018的所有整数的和为-2 019.故选B.9. D【解析】最高成绩为90+10=100,故A错误;最低成绩为90+(-7)=83分,故B错误;平均分为:90+15[1+(-2)+10+(-7)+0]=90.4,C错误,D正确.故选D.10. A【解析】(-2错误!未找到引用源。

有理数的加法(二)
互为相反数的两数的和为0. 加法的交换律:a+b=b+a 加法的结合律:(a+b)+c=a+(b+c)例(1)-2+2=0 (2) 0.6+(-0.6)=0 (3)(-3/5)+(+3/5)=0 (4)a+(-a)=0
1 填空
1)如果X与3的和为0,那么X的值为___。
2)绝对值不大于8的所有整数的和为___。
3)如果两个加数的和为0,其中一个加数为-1/3,则另一个加数为___。
4)有理数2、10、0,-14的和为___。
5) -1+2=___,7+(-2)=___。
6) 3.5的相反数与2的和为___。
7) 有理数a与-3的相反数的和为0,则a的值为___。
8)有理数a与b互为相反数,那么a+b=___。
9)某地一天早晨的气温是-6 0C,中午气温上升了12 0C,半夜气温又上升了-4 0C,半夜气温是___。
2 计算
1)-3+5 2)-8/13+1/26 3)(-1/2)+(-1/3) 4)-2.7+(-3.6)
3 纽约与北京的时差*为-13小时,小明在北京乘坐早晨8:00的航班飞行大约20小时后到达纽约,那么小明在到达时纽约的时间大约是几点?
4 某中学对七年级女生进行了仰卧起坐进行了测试,以能做20个为标准,超
过的次为正数,不足的次数用负数表示,这8名女生的成绩如下:
+5 , 0 ,-2 ,+4 , 2, -1 , 3 , -1
1)这8个女生有几个达到标准?
2)她们共做了多少个仰卧起坐?
5 若|X-3|与|2y-4|互为相反数,求3x+y的值。
有理数的加法
教学目标:
知识与技能:
1、理解有理数加法的意义,掌握有理数加法法则中的符号法则和绝对值运算法则;
2、能根据有理数加法法则熟练地实行有理数加法运算,弄清有理数加法与非负数加法的区别;
3、本节课通过行程问题说明有理数的加法法则的合理性,然后又通过实例说明如何使用
法则实行计算,让学生感知到数学知识来源于生活,并应用于生活。
教学重点:依据有理数的加法法则熟练实行有理数的加法运算。
教学难点:有理数的加法法则的理解
教学准备:多媒体教室,配套课件。
教学过程:
一、引入,
师:同学们,老师听说了一个很有意思发生在南方的故事,是一个数学计算题,题目是,小明去商场花60 元买了一个好看的书包,回家后碰到了小刚,小刚非常喜欢小明的包,愿意花70 元买走此包,小明同意
了。
第二天,小红也非常喜欢此包,于是找到了小明,希望小明能够想办法,帮忙从小刚手里转卖给她,
自己愿意花90 元,于是小明花了80 元从小刚手里买回了包,接着卖给小红90 元。
问题是,在整个过程中,小明一共赚了多少钱?
生1 :很简单,赚了10 元钱。
理由是,第一次卖,赚了10 元钱,第二次买,亏本10 元
钱,再卖,又赚了10元钱。
所以一共赚了10 元钱。
生2 :赚了30 元钱。
理由是,第一次卖,赚了10 元钱,第二次又赚了10 元钱,第三次又赚了10元钱,所以一共赚了30 元钱。
生3:赚了20 元钱。
老师:商人的做法是,这就是两次生意,第一次进价是60 元,卖70 元,赚了10 元钱;第二次进价是80 元,卖90元,又赚了10 元钱。
总共赚了20元钱。
商人的做法用纯数学的理论表示就是:-60+70-80+90=20 元。
师:同学们想像这个商人一样聪明吗?
生:想!
师:通过这节课的学习,同学们一定能学会!
、突出主题,突出主体师:看大屏幕,独立思考下列问题,然后回答问题。
某人从原点0 出发,如果第一次走了5米,第二次接着又走了3 米,求两次行走后某人在什么地方?
(两次行走后距原点0 为8 米,应该用加法。
) 为区别向东还是向西走,这里规定向东走为正,向西走为负.这两数相加有以下三种情况:
1. 同号两数相加
师:某人向东走 5米,再向东走 3 米,两次一共走了多少米? 这是求两次行走的路程的和.
生:5+3 = 8
师:很好,用数轴表示 师:从数轴上表明,两次行走后在原点 0 的东边 .离开原点的距离是 8 米 .所以两次一共向 东走了 8 米。
我们从这个图上得出说明结论呢?
生 1:生 2 :生 3 师:结论:正数加正数,其和仍是正数,和的绝对值等于这两个加数的绝对值的和。
2. 师:某人向西走 5 米,再向西走 3 米,两次一共向东走了多少米? 生:两次一共向西走了 8 米。
师:(-5)+(-3) = -8 用数轴表示如图。
师:从数轴上表明,两次行走后在原点 0 的西边,离开原点的距离是
8 米.所以两次一共
向东走了 -8 米。
我们从这个图上又能得出说明结论呢? 由学生讨论。
师生共同得出结论: 负数加负数, 其和仍是负数, 和的绝对值也是等于两个加数的绝对值 的和。
师:同号两数相加的规律生什么呢? 学生再讨论。
师生共同得出结论:同号两数相加,取相同的符号,并把绝对值相加。
2.异号两数相加 (1) 某人向东走 5米,再向西走 5米,两次一共向东走了多少米? 师:由数轴上表明,两次行走后,又回到了原点,两次一共向东走了多少米? 生:5+(-5) = 0
师:互为相反数的两个数相加,和为零。
(2) 某人向东走 5米,再向西走 3米,两次一共向东走了多少米? 师:两次行走后在原点 o 的东边,离开原点的距离是 2米.所以,两次一共向东走了 2 米. 生:5+(-3) = 2
(3) 某人向东走 3米,再向西走 5米,两次一共向东走了多少米? 师:同学们试着老师刚才的做法,画一个数轴,在数轴上表明两次行走的结果。
由学生讨论自己完成。
师:请同学们想一想, 异号两数相加的法则是怎么规定的?强调和的符号是如何确定的? 和的绝对值如何确定?
师生最后归纳: 绝对值不相等的异号两数相加, 取绝对值较大的加数的符号, 并用较大的 绝对值减去较小的绝对值,互为相反数的两个数相加得 0。
零与任何数相加等于任何数。
师: 如果我们把两个加数的和分为符号和绝对值两部分,
“正”相加和为正,两“负”相加和为负,异号相加跟着大(绝对值)
的跑 谣,同(两个加数同号)相加,异(两加数异号)相减(大减小)。
三、体现新时代教师是学生学习的合作者
在绝大部分学生完成课本阅读和解答好课本问题、 上述问题的基础上, 请学生们自主讨论、 复习本节课内容,以加深印象。
师:(强调)( 1)有理数加法法则;
( 2)养成算必讲理的良好习惯。
【课堂小结一改教师全盘包办,学生麻木的被“听”。
学生的课堂,让学生自己说,让学 生带着兴趣去学! 最大可能激发出学生的主观能动性。
为以后学习更复杂的数学计算打下深 厚的基础!】
四、基础巩固与知识延伸
1、口答竞赛:
(1)4+9;(2)4+(-9);(3)-4+9;(4)(-4)+(-9) ;(5)4+(-4) ;(6)9+(-2) ;(7)(-9)+2 ;(8)-9+0;
可把和的符号规律编成歌谣, 两 ;和的绝对值歌
2、计算
(1)5+(-22) ;(2)(-1.3)+(-8) ;(3)(-0.9)+1.5 ;(4)2.7+(-3.5) 、
五课堂小结:1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝
对值减去较小的绝对值,互为相反数的两个数相加得0。
零与任何数相加等于任何数。
六、布置作业
七、课后反思:
数学课堂中对概念的记忆非常重要。
歌德曾说:哪里没有兴趣,哪里就没有记忆。
在课堂的开始,通过一个非常感兴趣的故事开始,激发了学生的求知欲望;在课堂的末尾,协助他们从句子中提炼出朗朗上口“歌谣”,增强学生们记忆的兴趣,让他们带着兴趣记忆,达到了事半功倍的效果。