塑性力学复习纲要DOC
- 格式:doc
- 大小:1.26 MB
- 文档页数:17

复习纲要第一章绪论1.弹性与弹性变形物体受到不大的外力作用后产生的变形,在外力除去后可以全部恢复,物体仍保持原有的形状和尺寸。
这种性质称为材料的弹性,这种可以全部恢复的变形叫弹性变形。
这时称物体处于弹性状态。
2.塑性与塑性变形当外力超过一定限度后,在物体某些部分内,任意点上的应变将不随应力的消失而恢复。
这种变形不可恢复的性质称为塑性,不随应力消失而恢复的那部分变形称为塑性变形。
3.弹性区与塑性区在加载过程中,物体的一部分产生塑性变形时,称该部分已进入塑性状态,同时将该部分称为物体的塑性区,未进入塑性状态的区域则为弹性区。
4.塑性变形的特点(1)塑性应变和应力之间不再有一一对应的关系。
塑性变形不仅与当前的应力状态有关,还与加载的历史有关。
(2)应力与应变(或应变率)之间呈非线性关系。
5.塑性力学研究的主要内容(1)建立在塑性状态下应力与应变(或应变率)之间的关系。
(2)研究物体受外力作用进入塑性状态后产生的应力和变形,包括研究在加载过程中的每一时刻,物体内各点的应力和变形。
以及确定弹性区与塑性区的界限。
(3)有时根据需要还可以绕过加载过程中应力与变形的变化而直接去求物体达到极限状态(塑性变形无限制发展,物体已达到它对外力的最大承载能力)时的荷载,即极限荷载。
这种研究方法通常称为极限分析。
6.塑性力学的基本假设1、材料的塑性行为与时间、温度无关(在我们所研究的范围内,通常不考虑时间因素对变形的影响(如弹性后效、蠕变等),而且只限于考虑在常温下和缓慢变形的情形,所以也忽略温度和应变速度对材料性质的影响。
)2、材料具有无限的韧性3、材料是均匀的、连续的,并在初始屈服前为各向同性,且拉伸和压缩的应力-应变曲线一致;4、任何状态下的总应变可以分解为弹性和塑性两部分,且材料的弹性性质不因塑性变形而改变;5、对应于塑性变形部分的体积变化为零,静水压力不产生塑性变形。
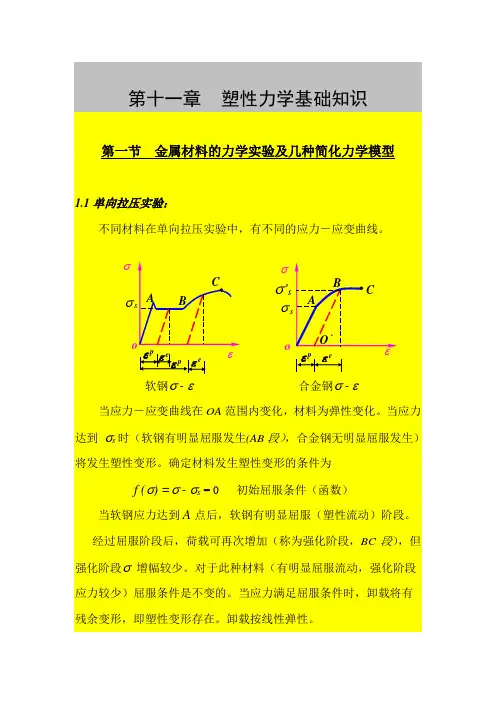
7.简单拉伸与压缩试验 (1)拉伸试验由拉伸应力—应变曲线可知:图1.1 图1.2①拉伸开始阶段σ和ε成正比,变形全是弹性的。

《弹塑性力学》复习提纲1. 弹性力学和材料力学在求解的问题以及求解方法方面的主要区别是什么?研究对象的不同:材料力学,基本上只研究杆状构件,也就是长度远远大于高度和宽度的构件。
非杆状结构则在弹性力学里研究研究方法的不同:材料力学大都引用一些关于构件的形变状态或应力分布的假定,得到的解答往往是近似的,弹性力学研究杆状结构一般不必引用那些假定,得到的结果比较精确。
并可用来校核材料力学得出的近似解。
2. 弹性力学有哪些基本假设?(1)连续性,(2)完全弹性,(3)均匀性,(4)各向同性,(5)假定位移和形变是微小的3. 弹性力学有哪几组基本方程?试写出这些方程。
(1)平面问题的平衡微分方程:平面问题的几何方程:平面应力问题的物理方程:(在平面应力问题中的物理方程中将E换为,换为就得到平面应变问题的物理方程)(2)空间问题的平衡微分方程;空间问题的几何方程;空间问题的物理方程:4. 按照应力求解和按照位移求解,其求解过程有哪些差别?(1)位移法是以位移分量为基本未知函数,从方程和边界条件中消去应力分量和形变分量,导出只含位移分量的方程和相应的边界条件,解出位移分量,然后再求形变分量和应力分量。
要使得位移分量在区域里满足微分方程,并在边界上满足位移边界条件或应力边界条件。
(2)应力法是以应力分量为基本未知函数,从方程和边界条件中消去位移分量和形变分量,导出只含应力分量的方程和边界条件,解出应力分量,然后再求出形变分量和位移分量。
满足区域里的平衡微分方程,区域里的相容方程,在边界上的应力边界条件,其中假设只求解全部为应力边界条件的问题。
5. 掌握以下概念:应力边界条件和位移边界条件;圣文南原理;平面应力与平面应变;逆解法与半逆解法。
位移边界条件:若在部分边界上给定了约束位移分量和,则对于此边界上的每一点,位移函数u和v和应满足条件=,=(在上)应力边界条件:若在部分边界上给定了面力分量(s)和(s),则可以由边界上任一点微分体的平衡条件,导出应力与面力之间的关系式。


《塑性力学及成形原理》知识点汇总第一章绪论1.塑性的基本概念2.了解塑性成形的特点第二章金属塑性变形的物理基础1.塑性和柔软性的区别和联系2.塑性指标的表示方法和测量方法3.磷、硫、氮、氢、氧等杂质元素对金属塑性的影响4.变形温度对塑性的影响;超低温脆区、蓝脆区、热脆区、高温脆区的温度范围补充扩展:1.随着变形程度的增加,金属的强度硬度增加,而塑性韧性降低的现象称为:加工硬化2.塑性指标是以材料开始破坏时的塑性变形量来表示,通过拉伸试验可以的两个塑性指标为:伸长率和断面收缩率3.影响金属塑性的因素主要有:化学成分和组织、变形温度、应变速率、应力状态(变形力学条件)4.晶粒度对于塑性的影响为:晶粒越细小,金属的塑性越好5.应力状态对于塑性的影响可描述为(静水压力越大):主应力状态下压应力个数越多,数值越大时,金属的塑性越好6.通过试验方法绘制的塑性——温度曲线,成为塑性图第三章金属塑性变形的力学基础第一节应力分析1.塑性力学的基本假设2.应力的概念和点的应力状态表示方法3.张量的基本性质4.应力张量的分解;应力球张量和应力偏张量的物理意义;应力偏张量与应变的关系5.主应力的概念和计算;主应力简图的画法公式(...3.-.14..)应力张量不变量的计算...........122222223()2() x y zx y y z z x xy yz zx x y z xy yz zx x yz y zx z xyJ J Jσσσσσσσσστττσσστττστστστ=++=-+++++=+-++公式(...3.-.15..)应力状态特征方程.........321230J J J σσσ---= (当已知一个面上的应力为主应力时,另外两个主应力可以采用简便计算公式(...3.-.35..).的形式计算)6.主切应力和最大切应力的概念计算公式..(.3.-.25..).最大切应力.....)(21min max max σστ-= 7.等效应力的概念、特点和计算主轴坐标系中......公式..(.3.-.31..).8σ=== 任意坐标系中......公式..(.3.-.31a ...).σ=8.单元体应力的标注;应力莫尔圆的基本概念、画法和微分面的标注 9.应力平衡微分方程 第二节 应变分析1.塑性变形时的应变张量和应变偏张量的关系及其原因 2.应变张量的分解,应变球张量和应变偏张量的物理意义 2.对数应变的定义、计算和特点,对数应变与相对线应变的关系 3.主应变简图的画法 3.体积不变条件公式(...3.-.55..).用线应变....0x y z θεεε=++=;用对数应变.....(主轴坐标系中)........0321=∈+∈+∈ 4.小应变几何方程公式(...3.-.66..).1;()21;()21;()2x xy yx y yzzy z zx xz u u v x y x v v w y z yw w u z x zεγγεγγεγγ∂∂∂===+∂∂∂∂∂∂===+∂∂∂∂∂∂===+∂∂∂ 第三节 平面问题和轴对称问题1.平面应变状态的应力特点;纯切应力状态的应力特点、单元体及莫尔圆公式(...3.-.8.6.).12132()z m σσσσσ==+= 第四节 屈服准则1.四种材料的真实应力应变曲线 2.屈雷斯加屈服准则 公式(...3.-.96..).max 2s K στ== 3.米塞斯屈服准则公式(...3.-.10..1.).2222222262)(6)()()(K s zx yz xy x z z y y x ==+++-+-+-στττσσσσσσ 2221323222162)()()(K s ==-+-+-σσσσσσσ公式(...3.-.102...).s sσσσσ==== 4.两个屈服准则的相同点和差别点5.13s σσβσ-=,表达式中的系数β的取值范围 第五节 塑性变形时应力应变关系 1.塑性变形时应力应变关系特点 2.应变增量的概念,增量理论公式(...3.-.125...).'ij ij d d εσλ= 公式(...3.-.129...).)](21[z y x x d d σσσσεε+-=;xy xy d d τσεγ23= )](21[z x y y d d σσσσεε+-=;yz yz d d τσεγ23=)](21[y x z z d d σσσσεε+-=;zx zx d d τσεγ23=3.比例加载的定义及比例加载须满足的条件 第六节 塑性变形时应力应变关系 1.真实应力应变曲线的类型第四章 金属塑性成形中的摩擦1.塑性成形时摩擦的特点和分类;摩擦机理有哪些?影响摩擦系数的主要因素 2.两个摩擦条件的表达式3.塑性成形中对润滑剂的要求;塑性成形时常用的润滑方法 第五章 塑性成形件质量的定性分析 1.塑性成形件中的产生裂纹的两个方面2.晶粒度的概念;影响晶粒大小的主要因素及细化晶粒的主要途径 3.塑性成形件中折叠的特征 第六章 滑移线场理论简介1.滑移线与滑移线场的基本概念;滑移线的方向角和正、负号的确定 2.平面应变应力莫尔圆中应力的计算;公式(...7.-.1.).ωτωσσωσσ2cos 2sin 2sin K K K xy m y m x =+=-= 3.滑移线的主要特性;亨盖应力方程公式(...7.-.5.).2ma mb ab K σσω-=± 4.塑性区的应力边界条件;滑移线场的建立练习题一、应力1、绘制⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=410140002ij σ的单元体和应力莫尔圆,并标注微分面。

结构力学计算复习大纲2011-9-19结构力学部分1.平面体系的机动分析1.1计算自由度1.2几何不变体系的基本组成规则1.3几何构造与静定性的关系2.静定梁、刚架、拱、桁架2.1 单跨和多跨的静定梁2.2 静定平面刚架2.3 三铰拱的计算和合理拱轴线2.4 静定平面桁架的计算3.结构位移的计算3.1 静定结构在荷载作用下的位移计算3.2 图乘法3.3 线弹性结构的互等定理4.力法4.1 力法的基本原理、典型方程和计算步骤4.2 超静定结构的位移计算4.3 温度变化、支座位移时超静定结构位移5.位移法5.1 转角位移方程5.2位移法的原理、典型方程和计算步骤5.3 对称性的利用6.能量法6.1 弹性体的应变能、应变余能、体积和形状变形应变能6.2 虚位移原理6.3 最小势能原理6.4 Ritz法、伽辽金法、功的互等定律7.矩阵位移法7.1 单元刚度矩阵及其坐标变换7.2 结构刚度矩阵和边界条件的引入7.3 非节点荷载的处理7.4 矩阵位移法的计算步骤8.影响线及其应用8.1 单跨梁的影响线8.2 多跨静定梁的影响线8.3 桁架的影响线8.4 超静定结构的影响线9.薄板的小挠度弯曲9.1 圆板和圆环的弯曲9.2 矩形薄板的弯曲计算力学部分1.平面杆系结构的有限元方法2.1 局部坐标系下的单元刚度矩阵2.2 单元刚度矩阵的坐标变换2.3 整体刚度矩阵的组集2.4 边界条件的引入和非节点荷载的处理2.平面问题的有限单元方法2.1 位移模式、应力矩阵2.2 单元刚度矩阵2.3 整体分析、整体刚度矩阵3.较精密的平面单元3.1 矩形单元3.2 六节点三角形单元3.3 等参数单元参考书目:[1] 李廉锟,结构力学,高等教育出版社[2] 刘尔烈等,有限单元法及程序设计,天津大学出版社。

塑性力学 第一章 绪 论§1-1 引 言1、研究对象及物点塑性体σεσε⎧⎪-⎨⎪⎩残余变形非线性关系非一一对应的-关系2、学习目的及要求1)掌握基本概念、原理和方法 2)基本应用及简例3)数值解法(有限元)、近似解法(属板变曲)4)为研究非线性材料(砼、岩石、土壤等)结构打下理论基础 3、主要参政书1)《工程塑性力学》,丁大钩、单炳样编 2)《塑性理论简明教程》徐秉业等编3)《塑性理论基础》卡恰诺夫著,周承倜等译 4)《有限元法读讲》,李大潜等编5)《弹性力学与塑性力学解题指导及习题集》徐秉业等编 6)《塑性力学基础》蒋泳秋、穆霞编 4、课程内容的安排 第一章 绪 论第二章 应力状态和应变状态(物理关系) 第三章 塑性理论基本方法 第四章 简单弹塑性问题第五章 理想刚塑性平面应变问题 第六章 塑性理论有限元法 第七章 剪板弹塑性弯曲§1-2 单向拉伸、静水压力(实验资料)1、单向拉伸 A —比例极限p σ B —弹性 e σ BC —屈服阶段屈服应力 D —强度极限B σ FG —卸 载 OG —残余变形应变的分解:(见下页图)e pe Eεεεσε=+=2、静水压力(各向均匀受压) 实验→结论1)体积应变(H )与压力P 基本上为线性关系2voH ap bp v ==-,2bp 很小2)H 为弹性的(卸载后完全恢复) 3)H 〈〈p x ε,……p exy r ……H~e x ε,……e xy r ……4)P 对屈服极限影响不大,可以忽略(不运合非金属材料) 根据以上的结论,塑性力学中通常忽略静水压力的影响。
§1-3简化模型1、理想弹塑性模型(低碳钢)2、线性强化弹塑性(高碳钢)3、幂强化模型§1-4三杆桁架的弹塑性分析,各杆面积A=1 1、平衡方程1212230p N N COSσ=+=2、几何关系1122312,cos303344vv hvvRδεδδεε=======变形协调条件3、物理关系(线性强化)1S()()() (>)Ss S SS SEEEεεεσσεεεσεεεε<⎧⎪===⎨⎪+-⎩(常数,用物理常数表示)4、弹性解由213(),4jσσ=(应力协调)12,1σσ>∴杆光屈服由1(),)(1k EV j p hσ=△弹性极限荷载13(1e p p σ==+弹性阶段,()()()121212,,,j k p v N N εεσσ−−→−−→−−→−−→ 5、弱塑性解12(,) s p p σσ>≤但1111221111 E (1)3(1)4((1)S i kjs s E EP V Ev E h E hE E EV h E Eεσσεσσ+-+++-=+-△当2s σσ=,开始全塑性,2S E εσ= 此时/111111()(1)S S Es S S E E E E εσσσεεεσ==+-+-1211132112(1)(1)44334(1)33jS Sj s S S E P PE EEV h E h h EE EP E E εσσσευσσ=+-++-=∴=++1=E 又6、塑性解122(,)s s p p σσσσ>>>(),()11111211(1)(1)](1(1)(1j k S S js E E pE E EEEV E h Eεσεσσ+-++-++-+7、全过程P-V 图对理想弹塑性或理想刚塑性材料,三杆全部进入塑性阶段后,P 不再增加而V 继续增加,2U P P =(极限荷载),对刚塑性,22)P P P P <<<时v=0,(P 时杆 对线性强化材料,不存在u p ,P 随υ不断增加受部分限制不变形,但在比例三阶段逐步减小,(刚速变小)8、卸载,重新加载(略)、荷载路径问题(略)第二章 应力状态和应变状态§2-1 点的应力状态1、应力解量ij σ (在直角坐标系i x 中) 下标 , j i 均从1至3变化i x ∴代表1,2,3(,,)x x x x y zij σ代表11,12,13,21,22,23,31,32,33σσσσσσσσσ 共九个分量,或,,,x xy xz z σττσij σ为二阶段对解量 2、斜面上的应力斜面法线N111122133112233cos()cos()cos() j jN X n N X m n N X n n T T e T e T e T e =======++=由平衡条件111112213322112222333311322333T n n n T n n n T n n n σσσσσσσσσ=++⎫⎪=++⎬⎪=++⎭或i ij j T n σ=3、应力能量的坐标变换原点标系:1,2,3x x x 新点标系:1,2,3x x x ''' 方赂余弦:,cos()j j ij x x x '=原点坐标系中的解量ij σ在新坐标系中为i j σ'(分量不同,实则代表同一点的应力状态)则ij ik je ke σαασ'=上式由二阶解量坐标变换的通式直接换来,可按以下步骤验证:1)以垂直于i x '的面(法线为i x '为“斜面”)用式(2-1)求该面上应力在原坐标系中的三个分量,2)将上述应力向新坐标投影 还可以验证:ij σ'仍为对称能量特例:xy 平面内的平方应力,3x '与3x 重合,132331320αααα====设图2-1中N 为立向(,,)m n ,则下为立应力n σ,n σ与作用线N 重合,故123N N N T T m T nσσσ=== 上式右边与(2-1)右边相等,约2()0()0()0X N xy XZ xy y n yz xy xz n m n m n m n σστττσστττσσ⎫-++=⎪+-+=⎬⎪++-=⎭而2221m n ++=,,,m n 不可能均为零,故321230N N N I I I σσσ∆=-+-=其中 2222212332x y z mx y y z z x xy yz zxx y z xy yz zx x y yz xy I I I σσσσσσσσσστττσσστττστστ⎫=++=⎪⎪=++---⎬⎪=+--⎪⎭式(2-3)有三个实根1,2,3σσσ,其值与坐标系无关,故1I 、2I 、3I 与坐标系无关,称为应力能量的三个不变量。


塑性力学期末复习总结塑性力学—期末复习,,第一章绪论,弹性与弹性变形,塑性与塑性变形,塑性力学的基本假设,弹性区与塑性区,塑性变形的特点,塑性力学的主要研究内容,重点:基本概念简化模型,比例极限,弹性极限,屈服极限,虎克定律,强化阶段,塑性阶段,后继屈服极限,简单拉伸实验,压缩试验,包辛格效应,静水压力试验,简化模型,(1)理想塑性材料①理想弹塑性②理想刚塑性,(2)强化材料①线性强化弹塑性②线性强化刚塑性③幂强化,,第二章应力状态理论,一点的应力状态剪应力互等定理主应力应力张量不变量八面体应力,重点:一点的应力状态、平面应力状态和空间应力状态的基本公式,主应力与主平面,斜截面上的正应力和剪应力:,主应力方程:,应力张量不变量:,由主应力方程可求得三个主应力将求得的任一个主应力代入:,方向余弦满足条件:,即,联立得到,求出主应力所在平面方位,平均应力,应力球张量——不引起塑性变形,应力偏张量——引起塑性变形,,,,应力偏张量不变量,,八面体面(或等倾面),正应力和剪应力,,,,,=,等效应力(或应力强度),,,等效剪应力(或剪应力强度),最大最小剪应力:,,斜面Ⅲ上的剪应力,莫尔应力圆,表示应力状态的Lode参数:,,应力Lode参数的物理意义:,1、与平均应力无关,2、其值确定了应力圆的三个直径之比,3、如果两个应力状态的Lode参数相等,就说明两个应力状态对应的应力圆是相似的,即偏量应力张量的形式相同,Lode参数是排除球形应力张量的影响而描绘应力状态特征的一个参数。
它可以表征偏应力张量的形式。
,例2.1已知一点的应力状态由以下一组应力分量所确定,即======1,应力单位为MPa。
试求该点的主应力值。
,解:,解得主应力为:,代入,例2.2已知结构内某点的应力张量如式,试求该点的球形应力张量、偏量应力张量、等效应力及主应力数值。
,解:,等效应力:,主应力:,也可由主应力求等效应力,,第三章应变状态理论,小变形情况下,应变分量与位移分量的关系,(几何方程/柯西几何关系),,,,张量形式,重点:应变分量、主应变及应变不变量的定义,应变张量不变量,,,平均线应变,,应变球张量及偏张量,,,如体积不变,,应变偏张量不变量,,,,还可以写成:,,,八面体面上的正应变:,,剪应变:,,,等效应变(应变强度),,等效剪应变(剪应变强度),,Γ=,最大剪应变,,表示应变状态的Lode参数,,几何意义:应变莫尔圆上Q2A与Q1A之比,应变协调方程(判断某点应变场成立),保证物体在变形后不会出现‘撕裂’,‘套叠’的现象,,第四章屈服条件和塑性本构关系,重点:屈服条件、加载规律和塑性流动法则,屈服函数,应力空间,等倾线,π平面,屈服曲面和屈服轨迹,应变空间,π平面上的点所代表的应力状态是偏张量,其球张量为零,等倾线上的点所代表的应力状态是球张量,其偏张量为零,Tresca屈服条件,认为最大剪应力达到极限值时开始屈服:,Tresca屈服条件的完整表达式,Tresca屈服条件常用在主应力大小顺序为已知的问题上,p平面上的屈服曲线(正六边形),主应力空间内的屈服条件(正六边形柱面),平面应力状态的屈服条件(s3=0),常数k值由简单拉伸实验或纯剪实验确定,ss=2ts,Mises 屈服条件,用连接p平面上的Tresca六边形的六个顶点的圆来代替原来的六边形,即:,,,常数C值由简单拉伸实验或纯剪实验确定,在主应力空间中,Mises屈服面将是圆柱面,在的平面应力情形,Mises屈服条件可写成:,两种屈服条件的关系,若规定简单拉伸时两种屈服条件重合,则Tresca六边形内接于Mises圆,且,若规定纯剪时两种屈服条件重合,则Tresca六边形外接于Mises圆,且,加载条件和加载曲面,初始屈服曲面,加载曲面(后继屈服面),强化现象,加载函数,加载准则,对强化材料,对理想塑性材料,当采用Mises屈服条件时,当采用Mises屈服条件时,注意:加载或卸载都是对一个点上的整个应力状态而言。

《塑形力学》课程教学大纲课程名称:塑形力学英文名称:Mechanics of Plasticity课程编码:51416017学时/学分:36 / 2课程性质:必修适用专业:工程力学先修课程:材料力学、弹性力学一、课程的目的与任务塑性力学是固体力学的一个重要分支,是一门技术基础课程。
它与生产实践有着十分重要的联系。
开设塑性力学课程的目的是为了让力学专业的研究生学习和掌握塑性力学中的基本概念和处理问题的方法,包括变形体的模型,应变的表示方法,屈服条件的概念,Tresca及Mises屈服条件等,掌握形变理论与增量理论及有关基本内容,掌握简单弹塑性力学的分析求解方法,掌握平面弹塑性问题的滑移线方法等。
使学生能够正确地计算材料或结构超出弹塑性极限后的应力应变分布规律,充分发挥材料的潜能,并合理地制定出结构的安全系数,同时也为金属塑性加工工艺设计提供有用的数据和资料。
该课程要求学生在掌握塑性力学中的基本理论的方法的同时还学会运用所学理论处理和解决工程中简单相关问题的能力。
二、教学内容及要求第一章绪论教学目的和要求:了解课程的性质、任务和研究对象;了解变形体的模型、应变的表示方法,屈服条件的概念,Tresca及Mises屈服条件基本概念;理解并牢记形变理论与增量理论及有关基本内容;了解塑性变形的基本特征。
教学难点和重点:重点是屈服条件、Tresca及Mises屈服条件的概念;平面弹塑性问题的滑移线方法。
教学方法和手段:以讲授为主,辅以举例。
课时安排:2学时。
一、材料的塑性二、塑性力学的任务三、塑性力学的发展简史四、塑性力学与其它课程的联系复习与作业要求:塑形力学的基本任务,变形固体基本假设。
考核知识点:塑形力学的任务;塑形力学的发展史;塑形力学和其他学科的关系。
辅助教学活动:运用多媒体介绍背景知识。
第二章应力状态与应变状态教学目的和要求:目的应力张量、应变张量、应变率和应变增量的计算问题,也为求屈服强度和屈服函数等问题作准备。

塑性力学课程复习1. 名词解释:塑性变形:指物体在除去外力后所残留下来的永久变形在给定的外力下,物体的变形并不随时间而改变。
韧性与脆性:如果变形很久就破坏,便称是脆性的;如果经受了很大的变形才破坏,便称材料具有较好的韧性。
应变强化:材料在超过弹性极限以后,在任一点卸载后再重新加载,则新得到的屈服应力将大于初始屈服应力,即材料经过塑性变形后得到了强化,这种现象称为应变强化。
等向强化:拉伸时的强化屈服应力和压缩时的强化屈服应力(绝对值)始终是相等的,称为等向强化。
随动强化:考虑到包氏效应,认为拉伸屈服应力和压缩屈服应力(的代数值)之差,即弹性响应的范围始终是不变的,称为随动强化。
屈服面:Mises 屈服条件:Tresca 屈服条件:双剪应力屈服条件与最大偏应力屈服条件:加载面:Drucker 公设(33式子):正交流动法则:加载准则:全量理论:亦称为形变理论,它是研究用应变全量表示弹塑性应力应变关系的理论。
这个理论的数学表达式简单,但不能反应复杂的加载历史。
增量理论:亦称为塑性流动理论,它是用应变增量表示弹塑性本构关系的理论。
简单加载、简单加载定理、静力场与机动场、上限定理与下限定理。
2. 基本概念:1)弹塑性材料在简单拉压时的应力应变响应曲线;2)轴向拉伸时的塑性失稳;3)理想弹塑性材料简单桁架的弹性极限、塑性极限、卸载后的残余应力与残余变形、加载路径的影响;4)体积变形为弹性(塑性不可压缩)的概念;5)等效应力、等效剪应力、等效应变、等效剪应变定义公式;6)主应力空间中应力状态在π平面上的投影;7)初始各向同性材料在π平面上屈服曲线的对称性质;8)薄壁圆管试件在拉-扭载荷或内压-轴向拉伸载荷下的屈服条件;9)Tresca 屈服条件与Mises 屈服条件;10) Drucker 公设、加载面的外凸性、塑性流动的正交性及加载准则;11)与Mises 屈服条件相关连的正交流动定律与塑性本构关系;12)简单加载的概念;13)全量理论与增量理论。
研究生《弹塑性力学》教学大纲陈明祥一、应力分析二、应力矢量与应力张量的概念, 斜面应力公式, 平衡微分方程与力边界条件;应力分量的坐标变换;主应力、应力张量不变量和最大剪切应力;Mohr应力圆;应力张量的分解、偏应力张量及其不变量;八面体上的应力和等效应力;主应力空间与(平面三、应变变形和应变的概念;应变张量和几何方程;刚体转动与转动张量;体积应变;应变张量的性质;应变率和应变增量;变形协调方程。
四、弹性本构方程应力-应变关系的一般表达;各向异性线弹性体的本构方程;各向同性线弹性体的本构方程;弹性应变能与弹性应变余能。
五、弹性力学基本方程与求解方法弹性力学的基本方程;求解方法;解的基本性质;圣维南原理;空间问题求解实例。
六、平面问题平面问题分类;平面问题的基本方程;平面问题的应力解法与实例分析;极坐标表示的基本方程;使用极坐标求解的几个问题。
七、薄板弯曲板的基本概念与薄板的基本假定;应力应变与挠度的关系;薄板弯曲微分方程;薄板横截面上的内力及内力表示的平衡微分方程;薄板的边界条件;薄板的广义力、广义变形和应变能;考虑横向剪切的Mindlin板理论。
八、温度应力问题热传导基本概念;热弹性基本方程;求解方法与举例。
九、能量原理与变分方法可能功原理;虚位移原理与最小势能原理;使用位移变分原理近似求解;虚应弹塑性力学目录力原理、最小余能原理及其近似求解;卡氏定理;有限元方法的基本概念。
九、塑性力学的基本概念塑性力学的主要内容;有关塑性本构关系的基本试验资料;应力路径与加载历史的基本概念;塑性本构关系的主要研究内容和研究方法;塑性变形的物理机制。
十、屈服条件屈服条件的概念与假设, 屈服面在主应力空间中的一般形状;Tresca屈服条件;Mises屈服条件;Tresca屈服条件和Mises屈服条件的比较及实验验证;后继屈服面与内变量;一致性条件;硬化模型。
十一、塑性本构关系塑性应变增量的概念;加卸载判别准则;Drucker公设和Ilyushin公设;加载面外凸形和正交流动法则;塑性势理论;理想塑性材料的增量本构关系;硬化材料的增量本构关系;增量本构关系的一般表达;关于增量理论的讨论;全量理论及适用范围;十二、简单弹塑性边值问题增量和全量理论的边值问题;梁的弹塑性弯曲;理想塑性材料的厚壁圆筒受内压作用。
2019年塑性力学课程复习*1.名词解释:塑性变形、应变强化、等向强化、随动强化、屈服面、Mises屈服条件、Tresca屈服条件、加载条件与加载面、Drucker公设、正交流动法则、加载准则、静力场与机动场、用于极限分析的上限定理与下限定理。
塑性变形:物体在除去外力后所残留下来的永久变形,在给定的外力下,物体的变形并不随时间而改变(p1)应变强化:重新拉伸后,材料并不在初始屈服点处进入塑性状态,而是在最后的卸载点附近进入塑性状态。
进入塑性状态后,应力应变曲线渐与初始应力应变曲线重合。
经历塑性变形后,材料受到了强化,屈服应力有了提高。
这种现象称为应变强化或应变硬化。
(p4)等向强化:认为拉伸时的强化屈服应力和压缩时的强化屈服应力绝对值相等。
也就是说当在拉伸变形时使得材料强化时,这种强化作用对拉伸和压缩都是相同的。
即压缩屈服应力得到了相同的提高。
随动强化:考虑到包兴格效应,认为拉伸屈服应力和压缩屈服应力(代数值)之差是不变的。
也就是弹性响应的范围始终不变。
屈服面:在复杂应力状态下。
初始弹性状态的界限为屈服条件,若以σij 作为坐标轴,屈服条件用F(σij)=0表示,则应力空间中F=0将表示为一个曲面,称为屈服曲面。
Mises屈服条件:注意到Tresca屈服条件不考虑中间主应力的影响,主方向不知道的情况下用J’2=0去拟合实验点,并称之为Mises屈服条件。
Tresca屈服条件:当最大剪应力达到某一极限值k时,材料开始产生屈服。
如果规定σ1 >=σ2 >=σ3,Tresca屈服条件可写为τmax=(σ1 -σ3)/2=k加载条件与加载面:经过变化的屈服条件称之为加载条件;在应力空间中对应的表面称为加载面。
Drucker公设:单轴实验表明,在平面上,回路(1)→(2)→(3)总是顺时针的。
这表明在一个应力闭循环中,需要外界注入功而不可能提取有用功。
在三维应力状态,这一性质可以表述为:当材料的物质微元在应力空间的任意应力闭循环中的余功非正时,即称材料满足Drucker公设。
《弹塑性力学》课程第一篇 基础理论部分第一章 应力状态理论1.1 基本概念1. 应力的概念应力:微分面上内力的分布集度。
从数学上看,应力sPF s ∆∆=→∆0lim ν由于微分面上的应力是一个矢量,因此,它可以分解成微分面法线方向的正应力νσ和微分面上的剪应力ντ。
注意弹塑性力学中正应力和剪应力的正负号规定。
2. 一点的应力状态(1)一点的应力状态概念凡提到应力,必须同时指明它是对物体内哪一点并过该点的哪一个微分面。
物体内同一点各微分面上的应力情况,称为该点的应力状态。
(2)应力张量物体内任一点不同微分面上的应力情况一般是不同的,这就产生了一个如何描绘一点的应力状态的问题。
应力张量概念的提出,就是为了解决这个问题。
在直角坐标系里,一点的应力张量可表示为⎪⎪⎪⎪⎭⎫⎝⎛=z zy zx yz yyx xz xy x ij στττστττσσ若已知一点的应力张量,则过该点任意微分面ν上的应力矢量p就可以由以下公式求出:n m l p xz xy x x ττσν++= (1-1’a ) n m l p yz y yx y τστν++=(1-1’b )n m l p z zy zx z σττν++=(1-1’c )由式(1-1),还可进一步求出该微分面上的总应力p 、正应力νσ和剪应力v τ: 222z y x p p p p ++=(1-2a )nl mn lm n m l zx yz xy z y x τττσσσσν222222+++++=(1-2b )22ννστ-=p(1-2c )(3)主平面、主方向与主应力由一点的应力状态概念可知,通过物体内任一点都可能存在这样的微分面:在该微分面上,只有正应力,而剪应力为零。
这样的微分面即称为主平面,该面的法线方向即称为主方向,相应的正应力称为主应力。
主应力、主方向的求解在数学上归结为求解以下的特征问题:}{}]{[i n i ij n n σσ=(1-3)式中,][ij σ为该点应力张量分量构成的矩阵,n σ为主应力,}{i n 为主方向矢量。
《弹塑性力学》课程第一篇 基础理论部分第一章 应力状态理论1.1 基本概念1. 应力的概念应力:微分面上内力的分布集度。
从数学上看,应力sPF s ∆∆=→∆0lim ν由于微分面上的应力是一个矢量,因此,它可以分解成微分面法线方向的正应力νσ和微分面上的剪应力ντ。
注意弹塑性力学中正应力和剪应力的正负号规定。
2. 一点的应力状态(1)一点的应力状态概念凡提到应力,必须同时指明它是对物体内哪一点并过该点的哪一个微分面。
物体内同一点各微分面上的应力情况,称为该点的应力状态。
(2)应力张量物体内任一点不同微分面上的应力情况一般是不同的,这就产生了一个如何描绘一点的应力状态的问题。
应力张量概念的提出,就是为了解决这个问题。
在直角坐标系里,一点的应力张量可表示为⎪⎪⎪⎪⎭⎫⎝⎛=z zy zx yz yyx xz xy x ij στττστττσσ若已知一点的应力张量,则过该点任意微分面ν上的应力矢量p就可以由以下公式求出:n m l p xz xy x x ττσν++= (1-1’a ) n m l p yz y yx y τστν++=(1-1’b )n m l p z zy zx z σττν++=(1-1’c )由式(1-1),还可进一步求出该微分面上的总应力p 、正应力νσ和剪应力v τ: 222z y x p p p p ++=(1-2a )nl mn lm n m l zx yz xy z y x τττσσσσν222222+++++=(1-2b )22ννστ-=p(1-2c )(3)主平面、主方向与主应力由一点的应力状态概念可知,通过物体内任一点都可能存在这样的微分面:在该微分面上,只有正应力,而剪应力为零。
这样的微分面即称为主平面,该面的法线方向即称为主方向,相应的正应力称为主应力。
主应力、主方向的求解在数学上归结为求解以下的特征问题:}{}]{[i n i ij n n σσ=(1-3)式中,][ij σ为该点应力张量分量构成的矩阵,n σ为主应力,}{i n 为主方向矢量。
塑性力学复习纲要第一章绪论1.弹性与弹性变形物体受到不大的外力作用后产生的变形,在外力除去后可以全部恢复,物体仍保持原有的形状和尺寸。
这种性质称为材料的弹性,这种可以全部恢复的变形叫弹性变形。
这时称物体处于弹性状态。
2.塑性与塑性变形当外力超过一定限度后,在物体某些部分内,任意点上的应变将不随应力的消失而恢复。
这种变形不可恢复的性质称为塑性,不随应力消失而恢复的那部分变形称为塑性变形。
3.弹性区与塑性区在加载过程中,物体的一部分产生塑性变形时,称该部分已进入塑性状态,同时将该部分称为物体的塑性区,未进入塑性状态的区域则为弹性区。
4.塑性变形的特点(1)塑性应变和应力之间不再有一一对应的关系。
塑性变形不仅与当前的应力状态有关,还与加载的历史有关。
(2)应力与应变(或应变率)之间呈非线性关系。
5.塑性力学研究的主要内容(1)建立在塑性状态下应力与应变(或应变率)之间的关系。
(2)研究物体受外力作用进入塑性状态后产生的应力和变形,包括研究在加载过程中的每一时刻,物体内各点的应力和变形。
以及确定弹性区与塑性区的界限。
(3)有时根据需要还可以绕过加载过程中应力与变形的变化而直接去求物体达到极限状态(塑性变形无限制发展,物体已达到它对外力的最大承载能力)时的荷载,即极限荷载。
这种研究方法通常称为极限分析。
6.塑性力学的基本假设(1)材料是均匀连续的;(2)在进入塑性状态前为各向同性(特别说明时除外);(3)物体承受荷载之前处于没有初应力的自然状态。
在我们所研究的范围内,通常不考虑时间因素对变形的影响(如弹性后效、蠕变等),而且只限于考虑在常温下和缓慢变形的情形,所以也忽略温度和应变速度对材料性质的影响。
7.简单拉伸与压缩试验(1)拉伸试验由拉伸应力—应变曲线可知:图1.1 图1.2①拉伸开始阶段σ和ε成正比,变形全是弹性的。
P 点的纵坐标P σ称为比例极限。
②应力超过P σ后,σ与ε不再成正比,但变形仍是弹性的。
Q 点的纵坐标e σ称为弹性极限。
③应力超过e σ后,在SA 段内应力不再增加,而应变继续增长,这种现象称为屈服现象。
对应于R 点的应力称为上屈服极限,对应于SA 的应力称为下屈服极限。
一般把下屈服极限称为屈服极限,以s σ表示。
④对于没有明显的屈服阶段,常规定以产生某一指定的残余应变(例如0.2%时的应力作为屈服极限。
记为2.0σ。
常常认为(P σ=e σ=s σ),在σ≤s σ阶段,服从虎克定律σ=εE 。
这里E 是弹性模量,它也是σ—ε曲线初始直线段的斜率。
⑤A 点以后如欲继续产生变形,则需继续加载,σ—ε关系如曲线ABF ,这一阶段称为强化阶段。
在这一阶段中,任一点上曲线的斜率εσd d E =1称为强化模量,一般E 1<E 。
在进入塑性阶段(即应力σ≥s σ)以后,设从任一点B 处开始卸载,则σ—ε曲线为通过B 点且与初始直线段OP 平行的直线BCD ,当全部应力卸完时即达到横坐标轴上的D 点,原来在B 点时整个应变ε为OH ,卸载后DH 段消失,故DH 段即为相应于B 点的弹性应变e ε,而残余应变OD 段,即为相应于B 点的塑性应变p ε。
故有ε=e ε+p ε。
同时可以看出,卸载至任意点C 时,卸掉的应力σ'与恢复的应变ε'之间也应当服从虎克定律,即εσ'='E (见图1.1)由图1.1也可以看出BD 线上的C 点与OP 线上的C ‘点具有同样的纵坐标,也就是说受有同样大小的应力,而其横坐标,也就是产生的应变却完全不同。
这也说明在塑性力学中应力和应变没有一一对应的关系。
所产生的应变,不仅和所受的应力有关,而且和加载历史有关。
设从D 点再重新加载。
σ—ε曲线几乎完全沿原来的卸载直线DCB 上升,直至非常接近B 点处才略有弯曲最后到达BF 段上的一点S ‘,(非常接近B 点,也可以近似地认为与B 点重合)。
这样可以看到,经过一次塑性变形以后再重新加载的试件,其弹性段增大了(图中S ’点或B 点高于S 点),屈服极限提高了(可以认为S ‘点或B 点的纵坐标为重新加载时的屈服极限)。
这种现象称为强化现象,相当于S ’点或B 点的应力称为后继屈服极限。
自S ’点以后再继续加载时将仍沿原来未经卸载的σ—ε曲线S ‘F 前进。
⑥图1.1中σ—ε曲线至F 点后开始下降,这意味着应力降低而应变仍可继续增长,直至C 点试件破坏。
实际上这是由于在F 点处试件已开始出现颈缩现象,试件截面积A 与原始截面积A 0相差甚大,仍以A 0除P 得到的已不是试件的真实应力。
以瞬时截面积A 去除P 才可较真实地反映试件中的应力,这时AP=σ称为真应力。
图1.1中的虚线FG ’即表示在这一阶段真应力与应变之间的关系。
(2)压缩试验 Buschinger 效应试验表明,对大多数金属在小变形阶段,压缩σ—ε曲线与拉伸σ—ε曲线基本一致。
可认为两者的弹性模量,屈服极限是相同的,如图(a )所示。
(a ) (b )具有强化性质的材料在经过拉伸进入塑性以后再卸载并反向加载时会导致压缩屈服极限的降低,这种现象称为Bauschinger 效应。
(如图(b )所示)(3)静水压力试验在不太大的压力作用下,可以认为体积应变与静水压力p 呈线性关系:Kp=θ即对一般金属,体积应变完全是线性弹性的,并且静水压力不产生塑性变形,它对屈服极限的影响完全可以忽略不计。
8.几种简化模型 (1)理想塑性材料 ① 理想弹塑性模型对有相当长屈服阶段的材料可以假设这段水平线一直延伸直至破坏,而忽略后面的强化,这种模型叫做理想弹塑性模型。
如图(a )所示。
这种模型的材料应力应变关系为(a ) (b )⎪⎩⎪⎨⎧>≤=s ss E εεεσεεεσ当当 sgn式中sgn 为符号函数sgn ε=⎩⎨⎧<->。
当,当0 101εε② 理想刚塑性模型。
如果所研究的问题具有较大的塑性变形,因而弹性变形可以忽略时,可以假设无弹性变形,只有塑性变形。
这种模型叫做理想刚塑性模型。
如图(b )所示。
这种模型的材料的应力应变关系为εσσs g n s = (2)强化材料对没有明显屈服阶段的材料,不能将进入塑性状态以后的应力应变关系用一条水平线来描述,根据曲线的形状可以采用以下几种模型:(a ) (b ) (c )① 线性强化弹塑性模型图(a )所示为线性强化弹塑性模型,它的应力应变关系为:⎪⎩⎪⎨⎧>-+≤=s s s s E E εεεεεσεεεσ当当sgn )]([ 1② 线性强化刚塑性模型如果可以忽略弹性变形,即成为图(b )所示的线性强化刚塑性模型,其应力应变关系为:εεεσσsgn )]([1s s E -+=③ 幂强化模型曲线如图(c )所示,其应力应变关系为:εεσsgn nB =其中0≤n ≤1,当n =1时,成为直线方程εσB =,服从虎克定律(此时B =E )。
当n =0时,成为εσsgn B =,成为理想刚塑性模型(此时B=s σ)。
第二章 应力状态和应变状态1.应力张量及其分解图2.1 图2.2取直角坐标系x ,y ,z ,则物体内任意点处的应力状态可以表示为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡z zy zx yz y yx xz xy x στττστττσ 或ij σ=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211 σσσσσσσσσ由剪应力互等定理知yz zy xz zx yx xy ττττττ=== , , 。
2.主应力及主平面及其求法物体每一点都存在三个互相正交的平面,在其上只有正应力而没有剪应力,称为主平面,其上的正应力称为主应力。
设通过一点的某截面的法线n 的方向余弦为l x ,l y ,l z ,或者简记为l i (i =1,2,3)。
则有 斜截面上的正应力:n σ=ij σl i l j =133221232221222l l l l l l l l l zx yz xy z y x τττσσσ+++++斜截面上的剪应力:2222222n z y x n n p p p p σστ-++=-=其中p 是斜截面上的总应力。
主应力方程: 其中,以求得的任一个主应力σj (j = 1,都可以得到关于I 1,I 2,I 3联立可解出主应力σj (j = 1,2 3叫做平均应力。
在各方向同时作用有大小为m σ的应力时,相当于静水压力(或反向的静水压力),它不产生塑性变形,所以从应力张量中将各向相同的分离出来,对于研究塑性变形更为方便,即* 如果令则*ijs称为应力偏张量,简称应力偏量,引起塑性变形。
当x,y还可写为:ijijjiijzxyzxyzyxsssssssJ2121)](2[212222222==+++++=τττkjjkijxzzxzyyzyxxyzxyzxyzyxssssssssssssJ31)](3)(3)(36[312223333=+++++++++=ττττττ4.几种特定截面上的应力图2.3 图2.4在图2.4中,主平面用Ⅰ表示,Ⅱ表示与三个主轴成相等倾斜角的斜截面,称为八面体面(或等倾面)。
其方向余弦为:⎪⎪⎪⎪⎪⎪⎬⎫±=±=±=313131321lll八面体面上的正应力:八面体面上的剪应力:也就是说,i 代替。
也就是说,来代替。
图2.4中斜面Ⅲ上的剪应力:⎪⎪⎪⎭⎪⎪⎪⎬⎫-=-=-=222213312321σστσστσστσ1≥σ2≥σ3,则5.三维应力圆 在图2.5中的σ轴上取OP 1、OP 2、OP 3之长分别等于三个主应力σ1、σ2、σ3,以P 2P 3,P 1P 3 ,P 1P 2为直径作三个圆,命名为圆A ,圆B 及圆C ,则圆A 即代表平行于σ1的所有截面上的正应力和剪应力,圆B 和C 分别代表平行于σ2和平行于σ3所有截面上的正应力和剪应力。
阴影区则表示不与任何主应力平行的斜截面上的正应力和剪应力。
在σ轴上取OM =σm ,并将τ轴移至过M 点处,则在以M 为原点的σ、τ'轴上,此三维应力圆即为应力偏张量的应力圆。
此时有图2.5 MP 1 = 11s m =-σσMP 2 =22s m =-σσMP 3 = 33s m =-σσ三维应力圆以及应力偏张量是由P 1、P 2 ,P 3三点的相对位置来确定的。
(1)单向拉伸:321,有:σ=-1。
(2)纯剪切:312,0σσσ-==,有:σμ=0。
(3)单向压缩:0,0321<==σσσ,有σμ=1 6.应变张量及其分解、应变不变量在小变形情况下,应变分量与位移分量的关系为:⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂==∂∂=∂∂+∂∂==∂∂=∂∂+∂∂==∂∂=z u x w z w y w z v y v x v y u x u xz zx z zy yz y yx x x γγεγγεγγε , , ,y因为xz zx zy yz yx xy γγγγγγ=== , ,,所以,决定应变状态的独立应变分量有六个。