
二次函数动点问题的学习归纳
模式1:平行四边形
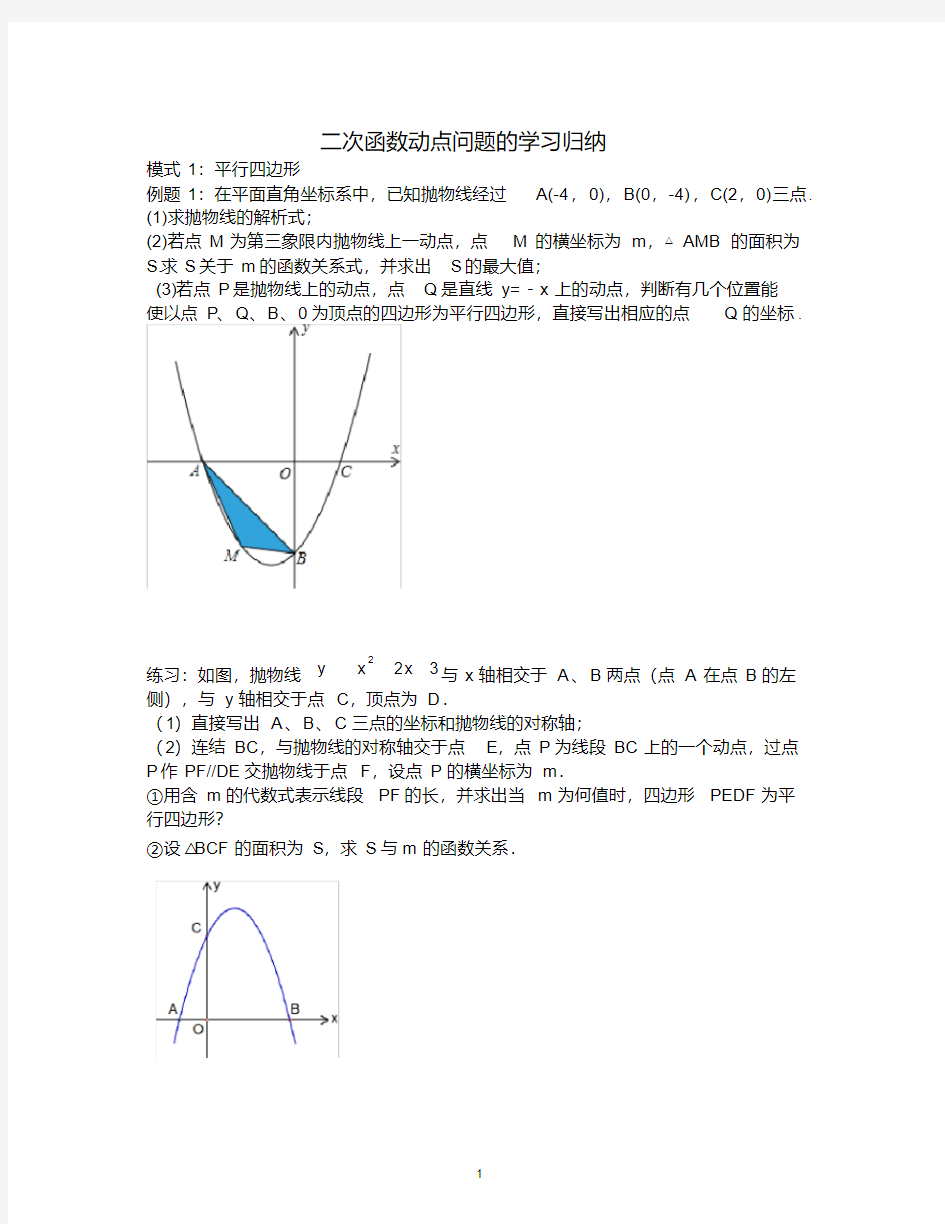
例题1:在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值;
(3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.
练习:如图,抛物线322
x x y
与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .
(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;
(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF//DE 交抛物线于点F ,设点P 的横坐标为m .
①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.
例题2:如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次函数
y=ax2+bx+c的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2.
(1)求二次函数y=ax2+bx+c的解析式;
(2)设一次函数y=0.5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.
练习:如图1,直线
4
3
4
x
y
和x轴、y轴的交点分别为B、C,点A的坐标是
(-2,0).
(1)试说明△ABC是等腰三角形;
(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他
们都停止运动.设M运动t秒时,△MON的面积为S.
①求S与t的函数关系式;
②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t 值;若不存在请说明理由;
③在运动过程中,当△MON为直角三角形时,求t的值.
A B C
O
P Q
D y
x
例题3:已知:如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE DC ,交OA 于点E .
(1)求过点E 、D 、C 的抛物线的解析式;
(2)将△EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的
横坐标为65
,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.
练习:已知抛物线y =ax 2+bx +c(a >0)经过点B(12,0)和C(0,-6),对称轴x =2.
(1)求该抛物线的解析式.
(2)点D 在线段AB 上且AD =AC ,若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一个动点Q 以某一速度从C 出发沿线段CB 匀速运动,问是否存在某一时刻,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t(秒)和点Q 的运动速度;若存在,请说明理由.
(3)在(2)的结论下,直线x =1上是否存在点M ,使△MPQ 为等腰三角形?若存在,请求出所有点M 的坐标;若不存在,请说明理由.
例题4:已知:在平面直角坐标系中,抛物线32x ax y (0a )交x 轴于
A 、
B 两点,交y 轴于点
C ,且对称轴为直线2x
.(1)求该抛物线的解析式及顶点D 的坐标;
(2)若点P (0,t )是y 轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD 的面积为S ,令W =t ·S ,当0<t <4时,
W 是否有最大值?如果有,求出W 的最大值和此时t 的值;
如果没有,说明理由;
探究二:如图2,是否存在以P 、A 、D 为顶点的三角形与Rt △AOC
相似?如果存在,求点P 的坐标;如果不存在,请说明理由.
练习:如图,已知抛物线经过A (﹣2,0),B (﹣3,3)及原点O ,顶点为C
(1)求抛物线的函数解析式.
(2)设点D 在抛物线上,点E 在抛物线的对称轴上,且以AO 为边的四边形AODE 是平行四边形,求点D 的坐标.
(3)P 是抛物线上第一象限内的动点,过点P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以P ,M ,A 为顶点的三角形与△BOC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.
y
x
O C
B A
D
二次函数的动点问题 1.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒. (1)求正方形ABCD 的边长. (2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度. (3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标. (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =o ∠的点P 有 个. (抛物线()2 0y ax bx c a =++≠的顶点坐标是2424b ac b a a ?? -- ??? ,.
[解] (1)作BF y ⊥轴于F . ()()01084A B Q ,,,, 86FB FA ∴==,. 10AB ∴=. (2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=Q ,. P Q ∴,两点的运动速度均为每秒1个单位. (3)方法一:作PG y ⊥轴于G ,则PG BF ∥. GA AP FA AB ∴ =,即610 GA t =. 35GA t ∴=. 3 105OG t ∴=-. 4OQ t =+Q , ()113410225S OQ OG t t ? ?∴= ??=+- ?? ?.
y x O 二次函数中的动点问题(二) 平行四边形的存在性问题 一、技巧提炼 1、二次函数y=ax 2 +bx+c 的图像和性质 a >0 a <0 图 象 开 口 对 称 轴 顶点坐标 最 值 当x = 时,y 有最 值是 当x = 时,y 有最 值是 增减 性 在对称轴左侧 y 随x 的增大而 y 随x 的增大而 在对称轴右侧 y 随x 的增大而 y 随x 的增大而 2、平行四边形模型探究 如图1,点A ()11,x y 、B ()22,x y 、C ()33,x y 是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D ,使得以A 、B 、C 、D 四点为顶点的四边形为平行四边形,如果存在,请求出点D 的坐标。 A B C x y 图1 图2 如图2,过A 、B 、C 分别作BC 、AC 、AB 的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。
由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。 3、平面直角坐标系中直线和直线l2: 当l1∥l2时k1= k2; 4、二次函数中平行四边形的存在性问题: 解题思路:(1)先分类(2)再画图(3)后计算 二、精讲精练 1、已知抛物线y=ax2+bx+c与x轴相交于A、B两点(A、B分别在原点的左右两侧),与y轴正半轴相交于C 点,且OA:OB:OC=1:3:3,△ABC的面积为6,(如图1) (1)求抛物线的解析式; (2)坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形若存在,请求出点M的坐标;若不存在,请说明理由; (3)如图2,在直线BC上方的抛物线上是否存在一动点P,△BCP面积最大如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.
一、二次函数线段最值问题 1、平行于x轴的线段最值问题 1)首先表示出线段两个端点的坐标 2)用右侧端点的横坐标减去左侧端点的横坐标 3)得到一个线段长关于自变量的二次函数 4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值 2、平行于y轴的线段最值问题 1)首先表示出线段两个端点的坐标 2)用上面端点的纵坐标减去下面端点的纵坐标 3)得到一个线段长关于自变量的二次函数解析式 4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值 3、既不平行于x轴,又不平行于y轴的线段最值问题 1)以此线段为斜边构造一个直角三角形,并使此直角三角形的两条直角边分别平行于x轴、y轴 2)根据线段两个端点的坐标表示出直角顶点坐标 3)根据“上减下,右减左”分别表示出两直角边长 4)根据勾股定理表示出斜边的平方(即两直角边的平方和) 5)得到一个斜边的平方关于自变量的二次函数 6)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值 7)根据所求得的斜边平方的最值求出斜边的最值即可 二、二次函数周长最值问题 1、矩形周长最值问题 1)一般会给出一点落在抛物线上,从这点向两坐标轴引垂线构成一个矩形,求其周长最值 2)可先设此点坐标,点p到x轴、y轴的距离和再乘以2,即为周长 3)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值 2、利用两点之间线段最短求三角形周长最值 1)首先判断图形中那些边是定值,哪些边是变量 2)利用二次函数轴对称性及两点之间线段最短找到两条变化的边,并求其和的最小值3)周长最小值即为两条变化的边的和最小值加上不变的边长 三、二次函数面积最值问题 1、规则图形面积最值问题(这里规则图形指三角形必有一边平行于坐标轴,四边形必有一组对边平行于坐标轴) 1)首先表示出所需的边长及高 2)利用求面积公式表示出面积 3)得到一个面积关于自变量的二次函数 4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值 2、不规则图形面积最值问题 1)分割。将已有的不规则图形经过分割后得到几个规则图形 2)再分别表示出分割后的几个规则图形面积,求和 3)得到一个面积关于自变量的二次函数 4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值 或1)利用大减小,不规则图形的面积可由规则的图形面积减去一个或几个规则小图形的面积来得到
二次函数与几何图形结合 ---探究面积最值问题 〖方法总结〗: 在解答面积最值存在性问题时,具体方法如下: ①根据题意,结合函数关系式设出所求点的坐标,用其表示出所求图形的线段长; ②观察所求图形的面积能不能直接利用面积公式求出,若能,根据几何图形面积公式得到点的坐标或线段长关于面积的二次函数关系式,若所求图形的面积不能直接利用面积公式求出时,则需将所求图形分割成几个可直接利用面积公式计算的图形,进行求解; ③结合已知条件和函数图象性质求出面积取最大值时的点坐标或字母范围。 (2014?达州)如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4). (1)求过O、B、A三点的抛物线的解析式. (2)在第一象限的抛物线上存在点M,使以O、A、B、M为顶点的四边形面积最大,求点M的坐标. (3)作直线x=m交抛物线于点P,交线段OB于点Q,当△PQB为等腰三角形时,求m的值.
(2014自贡)如图,已知抛物线c x ax y +- =232与x 轴相交于A 、B 两点,并与直线221-=x y 交于B 、C 两点,其中点C 是直线22 1-=x y 与y 轴的交点,连接AC . (1)求抛物线的解析式; (2)证明:△ABC 为直角三角形; (3)△ABC 内部能否截出面积最大的矩形DEFG ?(顶点D 、E 、F 、G 在△ABC 各边上)若能,求出最大面积;若不能,请说明理由.
(2014黔西南州)(16分)如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE. (1)求抛物线的函数解析式,并写出顶点D的坐标; (2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值; (3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
函数解题思路方法总结: ⑴求二次函数的图象与x轴的交点坐标,需转化为一元二次方程; ⑵求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶根据图象的位置判断二次函数ax2+bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断 图象的位置,要数形结合; ⑷二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸与二次函数有关的还有二次三项式,二次三项式ax2+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系: 动点问题题型方法归纳总结 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由. (3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标. 注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P 坐标----①C 为顶点时,以C 为圆心CM 为半径画弧,与对称轴交点即为所求点P ,②M 为顶点时,以M 为圆心MC 为半径画弧,与对称轴交点即为所求点P ,③P 为顶点时,线段MC 的垂直平分线与对称轴交点即为所求点P 。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC 平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。 共同点:
函数解题思路方法总结: ⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数ax 2+bx+c=0中a,b,c 的符号,或由二次函数中a,b,c 的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式ax 2+bx+c ﹙a ≠0﹚本身就是所含字母x 的二次函数;下面以a >0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系: 动点问题题型方法归纳总结 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。 二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式;
(2) 设抛物线的对称轴与x轴交于点M ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由. (3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标. 注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为 顶点时,以C为圆心CM为半径画弧,与对称轴交点即为所求点P,②M为顶点时,以M 为圆心MC为半径画弧,与对称轴交点即为所求点P,③P为顶点时,线段MC的垂直平 分线与对称轴交点即为所求点P。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值);方 法二,先求与BC平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。
二次函数的最值问题 二次函数2 (0)y ax bx c a =++≠是初中函数的主要内容,也是高中学习的重要基础.在初中阶段大家 本节我们将在这个基础上继续学习当自变量x 在某个范围内取值时,函数的最值问题.同时还将学习二次函数的最值问题在实际生活中的简单应用. 二次函数求最值(一般范围类) 例1. 当22x -≤≤时,求函数2 23y x x =--的最大值和最小值. 例2. 当12x ≤≤时,求函数21y x x =--+的最大值和最小值. 例3. 当0x ≥时,求函数(2)y x x =--的取值范围. 例4. 当1t x t ≤≤+时,求函数215 22 y x x =--的最小值(其中t 为常数). 在实际生活中,我们也会遇到一些与二次函数有关的问题: 二次函数求最值(经济类问题) 例1.为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y (台)与补贴款额x (元)之间大致满足如图①所示的一次函数关系.随着补贴款额x 的不断增大,销售量也不断增加,但每台彩电的收益Z (元)会相应降低且Z 与x 之间也大致满足如图②所示的一次函数关系. (1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元? (2)在政府补贴政策实施后,分别求出该商场销售彩电台数y 和每台家电的收益Z 与政府补贴款额x 之间的函数关系式; (3)要使该商场销售彩电的总收益w (元)最大,政府应将每台补贴款额x 定为多少?并求出总收益w 的最大值. 例2.凯里市某大型酒店有包房100间,在每天晚餐营业时间,每间包房收包房费100元时,包房便可全部租出;若每间包房收费提高20元,则减少10间包房租出,若每间包房收费再提高20元,则再减少10间包房租出,以每次提高20元的这种方法变化下去. (1)设每间包房收费提高x (元),则每间包房的收入为y 1(元),但会减少y 2间包房租出,请分别写出y 1、y 2与x 之间的函数关系式. (2)为了投资少而利润大,每间包房提高 x (元)后,设酒店老板每天晚餐包房总收入为y (元),请写出y 与x 之间的函数关系式,求出每间包房每天晚餐应提高多少元可获得最大包房费收入,并说明理由.
函数解题思路方法总结: ⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数ax 2+bx+c=0中a,b,c 的符号,或由二次函数中a,b,c 的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求与已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标、 ⑸ 与二次函数有关的还有二次三项式,二次三项式ax 2+bx+c ﹙a ≠0﹚本身就就是所含字母x 的二次函数;下面以a >0时为例,揭示二次函数、二次三项式与一元二次方程之间的内在联系: 二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)与点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上就是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由. (3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.
注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时,以C为圆心CM为半径画弧,与对称轴交点即为所求点P,②M为顶点时,以M为圆心MC为半径画弧,与对称轴交点即为所求点P,③P为顶点时,线段MC的垂直平分线与对称轴交点即为所求点P。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。 ①特殊四边形为背景; ②点动带线动得出动三角形; ③探究动三角形问题(相似、等腰三角形、面积函数关系式); ④求直线、抛物线解析式; ⑤探究存在性问题时,先画出图形,再根据图形性质探究答案。 二次函数的动态问题(动点)
必修一二次函数在闭区间上的最值 一、 知识要点: 一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。一般分为:对称轴在区间的左边,中间,右边三种情况. 设f x ax bx c a ()()=++≠2 0,求f x ()在x m n ∈[],上的最大值与最小值。 分析:将f x ()配方,得顶点为--?? ???b a ac b a 2442,、对称轴为x b a =-2 当a >0时,它的图象是开口向上的抛物线,数形结合可得在[m ,n]上f x ()的最值: (1)当[] -∈b a m n 2,时,f x ()的最小值是f b a ac b a f x -?? ???=-2442,()的最大值是f m f n ()()、中的较大者。 (2)当[]-?b a m n 2,时 若-最新二次函数最值问题类型题总结
二次函数 y = ax 2 bx c(a = 0)的最大值或最小值问题 知识点:1、配方法:将二次函数的一般式 y =ax 2 ? bx c(a =O,a,b,c 都是常数)化为顶 点式 y=a(x+m$+k (1 )若a 0,y 有最小值?当x - _m 时,y 取得最小值k (2)若a :::0,y 有最大值?当x 二_m 时,y 取得最大值k (2)若a ::: 0,y 有最大值,没有最小值,当 考察方向:一、1、已知二次函数的图像确定二次函数的最值 2 例1、二次函数y =ax ? bx ? c(a =0)的部分图象如图1.3-3所示,则该函数有最 __________________ 值, 最值为 __________________ . ;①在函数整个定义域内求 函数最值 〔②在给定定义域区间范围内求函 数最值 ①在函数整个定义域内求函数最值 2、公式法:直接利用二次函数图像的顶点坐标 (1 )若a 0,y 有最小值,没有最大值,当 b 2a 4ac-b 2 4a x =「b 时, 2a 求解. 4ac-b 2 y 最小值二 ■ 4a 4ac-b 2 y 最大值- ■ 4a 2、已知二次函数表达式求函数最值
例2、二次函数2 y =X 2X -5有() A.最大值-5 B. 最小值-5 C.最大值-6 D. 最小值-6 ② 在给定定义域区间范围内求函数最值 二次函数在自变量m乞x空n的给定范围内,对应的图象是抛物线上的一段?那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值. 根据二次函数对称轴的位置,函数在所给自变量x的范围的图象形状各异. 下面给出些常见情况: 2 例3、当」2乞x^2时,求函数y = x -2x-3的最大值和最小值
函数性问题专题—动点问题 函数及其图象是初中数学中的主要内容之一,也是初中数学与高中数学相联系的纽带.它与代数、几何、三角函数等知识有着密切联系,中考命题中既重点考查函数及其图象的有关基础知识,同时以函数为背景的综合性问题也是命题热点之一,多数省市作压轴题.因此,在中考复习中,关注这一热点显得十分重要.以函数为背景的综合性问题往往都可归结为动点性问题,我们把它归纳为以下七种题型(附例题) 一、因动点而产生的面积问题 例1:如图10,已知抛物线P :y =ax 2 +bx +c (a ≠0 与x 轴交于A 、B 两点(点A 在x 轴的正半轴上,与y 轴交于点C ,矩形DEFG 的一条边DE 在线段AB 上,顶点F 、G 分别在线段BC 、AC 上,抛物线P 上部分点的横坐标对应的纵坐标如下: (1 求A 、B 、C 三点的坐标; (2 若点D 的坐标为(m ,0 ,矩形DEFG 的面积为S ,求S 与m 的函数关系,并指出m 的取值范围; (3 当矩形DEFG 的面积S 取最大值时,连接DF 并延长至点M ,使FM =k ·DF ,若点M 不在抛物线P 上,求k 的取值范围. 若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2、(3小题换为下列问题解答(已知条件及第(1小题与上相同,完全正确解答只能得到5分: (2 若点D 的坐标为(1,0 ,求矩形DEFG 的面积 . 例2:如图1,已知直线
12 y x =-与抛物线2 164 y x =- +交于A B ,两点. (1)求A B ,两点的坐标; (2)求线段A B 的垂直平分线的解析式; (3)如图2,取与线段A B 端点分别固定在A B ,两处.用铅笔拉着这根橡皮筋使笔尖P 在直线A B 动点P 将与A B ,构成无数个三角形,这些三角求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.图2 图1 图10 第-2-页共4页 例3:如图1,矩形ODEF 的一边落在矩形ABCO 的一边上,并且矩形ODE F ∽矩形ABCO ,其相似比为1 : 4,矩形ABCO 的边 AB=4,BC=4
二次函数与几何图形 模式1:平行四边形 分类标准:讨论对角线 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形,则可分成以下几种情况 (1)当边AB 是对角线时,那么有BC AP // (2)当边AC 是对角线时,那么有CP AB // (3)当边BC 是对角线时,那么有BP AC // 1、本题满分14分)在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.
2、如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系.
模式2:梯形 分类标准:讨论上下底 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成梯形,则可分成以下几种情况 (1)当边AB 是底时,那么有PC AB // (2)当边AC 是底时,那么有BP AC // (3)当边BC 是底时,那么有AP BC // 3、已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 3 2 -=与边BC 相交于点D . (1)求点D 的坐标; (2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式; (3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.
二次函数的最值问题 二次函数y ax2bx c ( a 0) 是初中函数的主要内容,也是高中学习的重要基 础.在初中阶段大家已经知道:二次函数在自变量x 取任意实数时的最值情 况(当 a 时, 函数在 x b处取得最小值4ac b2,无最大值;当 a 0时,函数在 x b处取得 2a 4a 2a 4ac b2,无最小 值. 最大值 4a 本节我们将在这个基础上继续学习当自变 量x 在某个范围内取值时,函数的最值问 题.同时还将学习二次函数的最值问题在实际生活中的简单应 用. 二次函数求最值(一般范围类) 例 1.当 2 x 2 时,求函数 y x22x 3 的最大值和最小值. 分析:作出函数在所给范围的及其对称轴的草 图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变 量x 的值. 解:作出函数的图象.当x 1时, y min 4 ,当 x 2 时, y max 5. 例 2.当 1 x 2 时,求函数yx2x 1的最大值和最小值. 解:作出函数的图象.当 x 1 时, y min1,当 x 2 时, y max5 . 由上述两例可以看到,二次函数在自变量 x 的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置,函数在所给自变量 x 的范围的图象形状各异.下面给出一些常见情况: 例 3.当 x 0 时,求函数y x(2 x) 的取值范围.
资料
解: 作出函数 y x(2 x ) x 2 2x 在 x 0 内的图 象. 可以看出: 当 x 1 时, y min 1,无最大值. 所以,当 x 0 时,函数的取值范围 是 y 1 . 例 4. 当 t x t 1 时,求函数 y 1 x 2 x 5 的最小值 (其中 t 为常 数 ). 2 2 分析: 由于 x 所给的范围随着 t 的变化而变化,所以需要比较对称轴与其范围的相 对位 置. 解: 函数 y 1 x 2 x 5 的对称轴为 x 1 .画出其草图. 2 2 1 5 (1 ) 当对称轴在所给范围左侧.即 t 1 时: 当 x t 时, y min t 2 t ; t 1 t 1 0 t 1 2 2 (2 ) 当对称轴在所给范围之间.即 时: 当 x 1时, y min 1 12 1 5 3; 2 2 (3 ) 当对称轴在所给范围右侧.即 t 1 1 t 0 时: 当 x t 1 时, y min 1 (t 1)2 (t 1) 5 1 t 2 3. 2 2 2 1 t 2 3, t 0 2 综上所述: y3,0 t 1 1 t 2 t 5 , t 1 2 2 在实际生活中,我们也会遇到一些与二次函数有关的问题: 二次函数求最值 ( 经济类问题 ) 例 1.为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定 对购买彩电的农户实行政府补贴. 规定每购买一台彩电, 政府补贴若干元, 经调查某商场销售彩电台数 y (台)与补贴款额 x (元)之间大致满足如图①所示的一次函数关系.随着补 贴款额 x 的不断增大, 销售量也不断增加, 但每台彩电的收益 Z (元)会相应降低且 Z 与 x 之间也大致满足如图②所示的一次函数关系.
2018年04月28日187****6232的初中数学组卷 一.解答题(共5小题) 1.如图,已知抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0)和点C(0,3). (1)求抛物线的解析式和顶点E的坐标; (2)点C是否在以BE为直径的圆上?请说明理由; (3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R 的坐标,若不存在,请说明理由. 2.如图,已知抛物线y=ax2+bx+c过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D. (1)求抛物线的解析式; (2)设点M(1,m),当MB+MD的值最小时,求m的值; (3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E 作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.
3.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(点A在点B的左侧),直线l与抛物线交于A,C两点,其中点C的横坐标为2. (1)求A,B两点的坐标及直线AC的函数表达式; (2)P是线段AC上的一个动点(P与A,C不重合),过P点作y轴的平行线交抛物线于点E,求△ACE面积的最大值; (3)若直线PE为抛物线的对称轴,抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点,则在x轴上是否存在一点N,使四边形DMNQ 的周长最小?若存在,求出这个最小值及点M,N的坐标;若不存在,请说明理由. (4)点H是抛物线上的动点,在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由. 4.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
二次函数求最值方法总结-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
XX 教育辅导教案 学生姓名 性别 年级 学科 数学 授课教师 上课时间 年 月 日 第( )次课 共( )次课 课时: 课时 教学课题 二次函数求最大值和最小值 教学目标 利用二次函数的图像和性质特点,求函数的最大值和最小值 教学重点 与难点 含有参数的二次函数最值求解。 课堂引入: 1) 由二次函数应用题最值求解问题引申至一般二次函数求最值问题,阐述二次函数求最值问题 方法的重要性(初高中衔接、高中必修一重点学习内容)。 2) 当22x -≤≤时,求函数223y x x =--的最大值和最小值. (引导学生用初中所学的二次函数知识求解,为下面引出二次函数求最值方法总结做铺垫) 二次函数求最值方法总结: 一、设)0(2≠++=a c bx ax y ,当n x m ≤≤时,求y 的最大值与最小值。 1、当0>a 时,它的图象是开口向上的抛物线,数形结合可求得y 的最值: 1) 当n a b m ≤-≤2时,a b x 2-=时,y 取最小值:a b a c y 442min -=;y 的最大值在m x =或n x =处取到。 2) 若m a b <-2,二次函数在n x m ≤≤时的函数图像是递增的,则m x =时,y 取最小值;则n x =时,y 取最大值。 若n a b >- 2,二次函数在n x m ≤≤时的函数图像是递减的,则n x =时,y 取最小值;则m x =时,y 取最大值。
【变式训练】 变式1、当12x ≤≤时,求函数21y x x =--+的最大值和最小值. 分析:作出函数在所给范围的及其对称轴的草图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值. 解:作出函数的图象.当1x =时,1max -=y ,当2x =时,5min -=y . 【例题解析】 例2、当1t x t ≤≤+时,求函数21522 y x x =--的最小值(其中t 为常数). 分析:由于x 所给的范围随着t 的变化而变化,所以需要比较对称轴与其范围的相对位置. 解:函数21522 y x x =--的对称轴为1x =.画出其草图. (1) 当对称轴在所给范围左侧.即1t >时: 当x t =时,2min 1522y t t =--; (2) 当对称轴在所给范围之间.即1101t t t ≤≤+?≤≤时: 当1x =时,2min 1511322 y =?--=-; (3) 当对称轴在所给范围右侧.即110t t +
中考二次函数动点问题(含答案) 1.如图①,正方形的顶点的坐标分别为,顶点在第一象限.点从点出发,沿正方形按逆时针方 向匀速运动,同时,点从点出发,沿轴正方向以相同速度运动.当点到达点时,两点同时停止 运动,设运动的时间为秒. (1)求正方形的边长. (2)当点在边上运动时,的面积(平方单位)与时间(秒)之间的函数图象为抛物线的一部分 (如图②所示),求两点的运动速度. (3)求(2)中面积(平方单位)与时间(秒)的函数关系式及面积取最大值时点的坐标.(4)若点ABCD保持(2)中的速度不变,则点ABCD沿着ABCD边运动时,ABCD的大小随着时间ABCD的增大而增大;沿着ABCD边运动时,ABCD的大小随着时间ABCD的增大而减小.当点ABCD沿着这两边运动时,使ABCD的点ABCD有个. (抛物线ABCD的顶点坐标是. [解] (1)作轴于. , . . (2)由图②可知,点从点运动到点用了10秒. 又. 两点的运动速度均为每秒1个单位. (3)方法一:作ABCD轴于ABCD,则ABCD. ABCD ,即 ABCD . ABCD .ABCD .ABCD,
ABCD . 即 ABCD . ABCD ,且 ABCD , ABCD当 ABCD 时,ABCD有最大值. 此时 ABCD , ABCD点ABCD的坐标为 ABCD .(8分) 方法二:当ABCD时, ABCD . 设所求函数关系式为. 抛物线过点, . ,且, 当时,有最大值. 此时, 点的坐标为. (4). [点评]本题主要考查函数性质的简单运用和几何知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难。 . 2. 如图①,中,,.它的顶点的坐标为,顶点的坐标为,,点从点出发,沿的方向匀速运动,同时点从点出发,沿轴正方向以相同速度运动,当点到达点时,两点同时停止运动,设运动的时间为秒. (1)求的度数. (2)当点在上运动时,的面积(平方单位)与时间(秒)之间的函数图象为抛物线的一部分,(如图②),求点的运动速度. (3)求(2)中面积与时间之间的函数关系式及面积取最大值时点的坐标. (4)如果点ABCD保持(2)中的速度不变,那么点ABCD沿ABCD边运动时,ABCD的大小随着时间ABCD的增大而增大;沿着ABCD边运动时,ABCD的大小随着时间ABCD的增大而减小,当点ABCD沿这两边运动时,使ABCD的点ABCD有几个?请说明理由. 解: (1)ABCD.
二次函数动点问题的学习归纳 模式1:平行四边形 例题1:在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标. 练习:如图,抛物线 322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF//DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系.
例题2:如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次函数 y=ax2+bx+c的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2. (1)求二次函数y=ax2+bx+c的解析式; (2)设一次函数y=0.5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标. 练习:如图1,直线 4 3 4 + - =x y 和x轴、y轴的交点分别为B、C,点A的坐标是 (-2,0). (1)试说明△ABC是等腰三角形; (2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S. ①求S与t的函数关系式; ②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t 值;若不存在请说明理由; ③在运动过程中,当△MON为直角三角形时,求t的值.
二次函数求最值参数分类讨论的方法 分类讨论是数学中重要的思想方法和解题策略,它是根据研究对象的本质属性 的相同点和不同点,将对象分为不同种类然后逐类解决问题. 一般地,对于二次函数y=a (x m )2+n ,x ∈[t ,s ]求最值的问题;解决此类问题的基本思路为:根据对称轴相对定义域区间的位置,利用分类讨论思想方法。为做到 分类时不重不漏,可画对称轴相对于定义域区间的简图分类。 ①表示对称轴在区间[t ,s ]的左侧,②表示对称轴在区间[t ,s ]内且靠近区 间的左端点,③表示对称轴在区间内且靠近区间的右端点,④表示对称轴在区间[t ,s ]的右侧。然后,再根据口诀“开口向上,近则小、远则大”;“开口向下,近则大、 远则小”即可快速求出最值。 含参数的二次函数求最值的问题大致分为三种题型,无论哪种题型都围绕着对称 轴与定义域区间的位置关系进行分类讨论 题型一:“动轴定区间”型的二次函数最值 例1、求函数2()23f x x ax =-+在[0,4]x ∈上的最值。 分析:先配方,再根据对称轴相对于区间的位置讨论,然后根据口诀写出最值。 解:222()23()3f x x ax x a a =-+=-+- ∴此函数图像开口向上,对称轴x=a ①、当a <0时,0距对称轴x=a 最近,4距对称轴x=a 最远, ∴x=0时,min y =3,x=4时,max y =19-8a ②、当0≤a<2时,a 距对称轴x=a 最近,4距对称轴x=a 最远, ∴x=a 时,min y =3-a2,x=4时,max y =19-8a ③、当2≤a<4时,a 距对称轴x=a 最近,0距对称轴x=a 最远, ① ② ③ ④ t t +s 2s
二次函数的动点问题 1如图,已知抛物线经过原点O 和x 轴上另一点A ,它的对称轴x =2 与x 轴 交于点C ,直线y =-2x -1经过抛物线上一点B (-2,m ),且与y 轴、直线x =2分别交于点D 、E . (1)求m 的值及该抛物线对应的函数关系式; (2)求证:① CB =CE ;② D 是BE 的中点; (3)若P (x ,y )是该抛物线上的一个动点,是否存在这样的点P ,使得PB =PE ,若存在,试求出所有符合条件的点P 的坐标;若不存在,请说明理由 分析 (1)由点B (-2,m )在直线12--=x y 上,可求得m 的值及 点B 的坐标,进而求得抛物线的解析式; (2)通过分别求得CB 和CE 的长来说明CB =CE, 过点B 作BG ∥x 轴,与y 轴交于F 、直线x =2交于G ,过点E 作EH ∥x 轴,交y 轴于H ,由△DFB ≌△DHE,证得D 是BE 的中点; (3)若存在点P 使得PB=PE,则点P 必在线段BE 的中垂线CD 上, 动点P 又在抛物线上,通过解直线CD 和抛物线对应的函数关系式所联列的方程组,其解即为所求点的坐标. 解(1)∵ 点B (-2,m ) 在直线12--=x y 上, ∴ m =-2×(-2)-1=3. ∴ B (-2,3) ∵ 抛物线经过原点O 和点A ,对称轴为x =2, ∴ 点A 的坐标为(4,0) . 设所求的抛物线对应函数关系式为y =a (x -0)(x -4). 将点B (-2,3)代入上式,得3=a (-2-0)(-2-4),∴ 4 1=a . ∴ 所求的抛物线对应的函数关系式为)4(41-= x x y ,即x x y -=24 1 . (2)①直线y =-2x -1与y 轴、直线x =2的交点坐标分别为D (0,-1) E (2,-5).
二次函数)0(2 ≠++=a c bx ax y 的最大值或最小值问题 知识点:1、配方法:将二次函数的一般式),,,0(2 都是常数c b a a c bx ax y ≠++=化为顶点式()k m x a y ++=2 (1)若0>a ,y 有最小值.当m x -=时,y 取得最小值k (2)若0a ,y 有最小值,没有最大值,当a b x 2-=时,a b a c y 442-=最小值. (2)若0 ①在函数整个定义域内求函数最值 例2、二次函数522-+=x x y 有( ) A.最大值5- B.最小值5- C.最大值6- D.最小值6- ②在给定 定义域区间范围内求函数最值 二次函数在自变量n x m ≤≤的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值. 根据二次函数对称轴的位置,函数在所给自变量x 的范围的图象形状各异.下面给出一些常见情况: 例3、当22≤≤-x 时,求函数322 --=x x y 的最大值和最小值