
有趣的“斐波那契数列”
“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契,他被人称作“比萨的列昂纳多”。1202年,他撰写了《珠算原理》一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。
斐波那契数列指的是这样一个数列:0,1,1,2,3,5,8,13,21……
一、生活中的斐波那契现象
1、细察下列各种花,它们的花瓣的数目具有斐波那契数:延龄草、野玫瑰、南美血根草、大
波斯菊、金凤花、耧斗菜、百合花、蝴蝶花。
2、细察以下花的类似花瓣部分,它们也具有斐波那契数:紫宛、大波斯菊、雏菊。
斐波那契数经常与花瓣的数目相结合:
3………………………百合和蝴蝶花
5………………………蓝花耧斗菜、金凤花、飞燕草
8………………………翠雀花
13………………………金盏草
21………………………紫宛
34,55,84……………雏菊
3、斐波那契数还可以在植物的叶、枝、茎等排列中发现。例如,在树木的枝干上选一片叶
子,记其为数0,然后依序点数叶子(假定没有折损),直到到达与那息叶子正对的位置,则其间的叶子数多半是斐波那契数。叶子从一个位置到达下一个正对的位置称为一个循回。叶子在一个循回中旋转的圈数也是斐波那契数。在一个循回中叶子数与叶子旋转圈数的比称为叶序(源自希腊词,意即叶子的排列)比。多数的叶序比呈现为斐波那契数的比。
二、在杨辉三角中隐藏着斐波那契数列
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……
过第一行的“1”向左下方做45度斜线,之后做直线的平行线,将每条直线所过的数加起来,即得一数列1、1、2、3、5、8……
三、斐波那契数列与黄金比值
相继的斐波那契数的比的数列:它们交错地或大于或小于黄金比的值。该数列的极限为。这种联系暗示了无论(尤其在自然现象中)在哪里出现黄金比、黄金矩形或等角螺线,那里也就会出现斐波那契数,反之亦然。
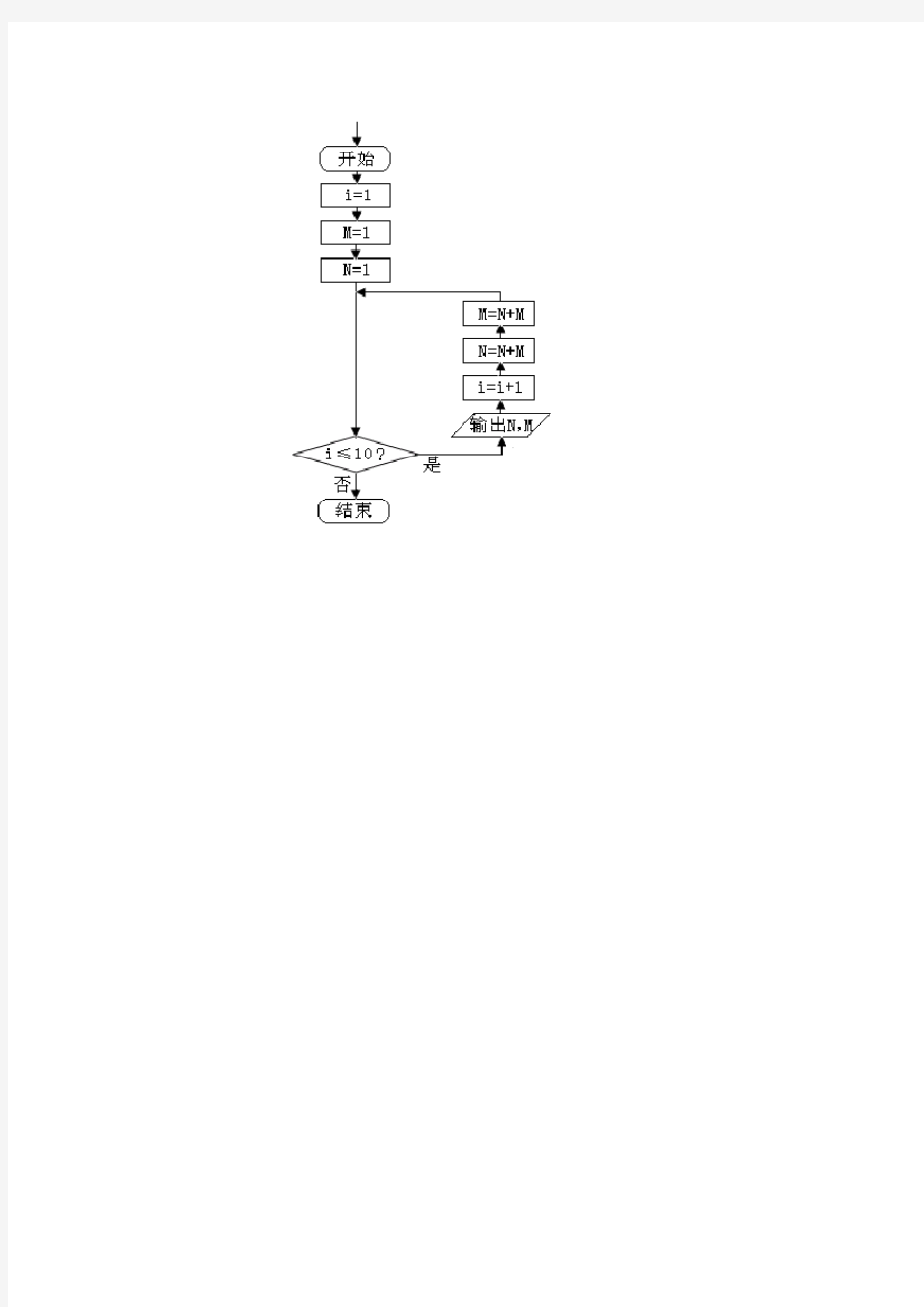
四、斐波那契数列蕴藏着算法思想
在科学计算中,有许多有规律的重复计算,如数列求项、求和等问题,非常适合计算机处理,需要借助于算法的循环结构。
例如:设{F
n }是斐波那契数列1、1、2、3、5、8、13、21、34、55、89……,则F
1
=F
2
=1,
F n =F
n-1
+F
n-2
画出程序框图,表示输出斐波那契数列的前20项。
斐波那契数列
斐波那契数列 一、简介 斐波那契数列(Fibonacci),又称黄金分割数列,由数学家斐波那契最早以“兔子繁殖问题”引入,推动了数学的发展。故斐波那契数列又称“兔子数列”。 斐波那契数列指这样的数列:1,1,2,3,5,8,13,……,前两个数的和等于后面一个数字。这样我们可以得到一个递推式,记斐波那契数列的第i项为F i,则F i=F i-1+F i-2. 兔子繁殖问题指设有一对新生的兔子,从第三个月开始他们每个月都生一对兔子,新生的兔子从第三个月开始又每个月生一对兔子。按此规律,并假定兔子没有死亡,10个月后共有多少个兔子? 这道题目通过找规律发现答案就是斐波那契数列,第n个月兔子的数量是斐波那契数列的第n项。 二、性质 如果要了解斐波那契数列的性质,必然要先知道它的通项公式才能更简单的推导出一些定理。那么下面我们就通过初等代数的待定系数法计算出通项公式。 令常数p,q满足F n-pF n-1=q(F n-1-pF n-2)。则可得: F n-pF n-1=q(F n-1-pF n-2) =q2(F n-2-pF n-3) =…=q n-2(F2-pF1) 又∵F n-pF n-1=q(F n-1-pF n-2) ∴F n-pF n-1=qF n-1-pqF n-2 F n-1+F n-2-pF n-1-qF n-1+pqF n-2=0 (1-p-q)F n-1+(1+pq)F n-2=0 ∴p+q=1,pq=-1是其中的一种方程组 ∴F n-pF n-1= q n-2(F2-pF1)=q n-2(1-p)=q n-1 F n=q n-1+pF n-1=q n-1+p(q n-2+p(q n-3+…))=q n-1+pq n-2+p2q n-3+…+p n-1 不难看出,上式是一个以p/q为公比的等比数列。将它用求和公式求和可以得到: 而上面出现了方程组p+q=1,pq=-1,可以得到p(1-p)=-1,p2-p-1=0,这样就得到了一个标准的一元二次方程,配方得p2-p+0.25=1.25,(p-0.5)2=1.25,p=±√1.25+0.5。随意取出一组解即可: 这就是著名的斐波那契数列通项公式。有了它,斐波那契数列的一些性质 也不难得出了。比如斐波那契数列相邻两项的比值趋向于黄金分割比,即:
生活中我们常常相信亲眼所见,但又常常为自己的眼睛所骗,魔术就是一个很好的例子。数学中也有这种欺骗我们眼睛的奇妙的数学魔术,我们还是来看一个简单的问题吧,将图3中面积为13×13=169的正方形裁剪成图中标出的四块几何图形,然后重新拼接成图4,计算可知长方形的面积为8×21=168,比正方形少了一个单位的面积,真不可思议! 这两个问题是这样的令人惊奇和难以理解,我们在白纸上将正方形量好画出,剪成四块,重新安排后拼成长方形,除非图形做得很大并且作图和剪裁都十分精确,我们一般是不会发现拼接成的长方形在对角线附近发生了微小的重叠,正是沿对角线的微小重叠导致了一个单位面积的丢失。要证实这一点我们只要计算一下长方形对角线的斜率和正方形拼接各片相应边的斜率,比较一下就会清楚了。 问题2中涉及到四个数据5、8、13和21,有一定数学基础的同学会认出这是著名的斐波那契数列中的四项,斐波那契数列的特征是它的每一项都是前两项之和:1,1,2,3,5,8,13,21,34,……。我们还可以使用这个数列中的其他相邻四项来试验这个过程,无论选取哪四项,都可以发现正方形和长方形的面积是不会相等的,有时正方形的面积比长方形多一个单位面积,有时则正好相反。多做几次上述实验,我们就会得出斐波那契数列的一个重要性质:这个数列任意一项的平方等于它前后相邻两项之积加1或减1。用公式表示就是:。其中表示正方形的面积,表示长方形的面积。知道了这个事实,我们就可以自己构造类似于问题2的几何趣题。 爬梯子问题(斐波那契数列应用) 1.小明要上楼梯,他每次能向上走一级、两级或三级,如果楼梯有10级,他有几种不同的走法? 这里我们不妨也来研究一下其中的规律:如果楼梯就一级,他有1种走法;如果楼梯有两级,他有2种走法;如果楼梯有三级,他有4种走法;如果有五级楼梯,他有7种走法. 既:楼梯的级数:12345678... 上楼梯的走法:124713244481... 这其中的规律就是,这里从第4个数开始,每一个数都等于它前面的3个数之和。
斐波那契数列与黄金分割 应用研究 作者姓名 院系6系 学号
摘要 “斐波那契数列(Fibonacci)”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年,籍贯大概是比萨)。他被人称作“比萨的列昂纳多”。斐波那契数列是一个古老而有趣的问题,由于其所具有的各种特殊属性,它与最优美的黄金分割有这密不可分的关系。在数学领域以及自然界中随处可见,而且正逐渐被应用在人们的日常生活与娱乐中。 关键词:斐波那契,黄金分割,应用 1 引言 斐波那契数列又称“斐波那契神奇数列”,是由13世纪的意大利数学家斐波那契提出的,当时是和兔子的繁殖问题有关的,它是一个很重要的数学模型。假设一对成年兔子放于围栏中,每月可生下一对一雌一雄的小兔,而小兔出生一个月后便可以生育小兔,且每月都生下一对一雌一雄的小兔.问把这样一对初生的小兔置于围栏中,一年后围栏中共有多少对兔子(假定兔子没有死亡)?据此,可得月份与兔子对数之间的对应关系如下: 月份0 1 2 3 4 5 6 7 ? 大兔对数0 1 1 2 3 5 8 13 ? 小兔对数 1 0 1 1 2 3 5 8 ? 兔子总对数 1 1 2 3 5 8 13 21 ? 如果用F n 表示第n个月兔子的总对数,那么F n能构成一个数列:1,1,2,3,5,8,13,21,34,55,89?.这个数列显然有如下的递推关系: F n =F n-1 +F n-2 (n>1,n为正整数),F0 =0,F1 =1 (1) 满足(1)式的数列就叫做斐波那契数列,这是一个带有初值的用递推关系表示的数列。这个数列一问世就吸引了无数数学家的兴趣,以下是费氏数列的定义及通项公式。 费氏数列是是由一连串的数字所组成的(1、1、2、3、5、8、13、…),而且这串数字之间具有一定的规则,就是每一个数字必须是前两个数字的和( an =
浅谈斐波那契数列的真善美 小七怪小组 摘要自斐波那契数列产生至今,人们对其研究的热情经久不衰。本文探究斐波那契数列的真、善、美,简单介绍斐波那契数列到底真在何处、善在何处、美在何处,并且得出斐波那契数列真、善、美三者之间的联系。 关键词斐波那契数列真善美 一、斐波那契数列的由来 13 世纪意大利数学家斐波那契在他的《算盘书》的修订版中增加了一道著名的兔子繁殖问题。问题是这样的:如果每对兔子(一雄一雌) 每月能生殖一对小兔子( 也是一雄一雌,下同)每对兔子第一个月没有生殖能力,但从第二个月以后便能每月生一对小兔子假定这些兔子都没有死亡现象,那么从第一对刚出生的兔子开始,12个月以后会有多少对兔子呢? 这个问题的解释如下:第一个月只有一对兔子;第二个月仍然只有一对兔子;第三个月这对兔子生了一对小兔子,共有1+l =2 对兔子;第四个月最初的一对兔子又生一对兔子,共有2+l =3对兔子;则由第一个月到第十二个月兔子的对数分别是: l , l , 2 , 3 , 5 , 8 ,13 , 21 , 34 , 55 ,89,144 , …… , 后人为了纪念提出兔子繁殖问题的斐波那契,将这个兔子数列称为斐波那契数列,学术界又称为黄金分割数列。 二、斐波那契数列与真 何为真?“真有两个含义, 一是指客观世界存在的客观物质, 二是指客观世界的本质规律。”[1]在自然界中,许多事物本身蕴含的规律都跟斐波那契数列有关。例如树木的生长,由于新生的枝条,往往需要一段“休息”时间,供自身生长,之后才萌发新枝。因此,一株树苗在一 段时间间隔后,例如一年,会长出一条新枝; 第二年新枝“休息”,老枝依旧萌发;此后, 老枝与“休息”过一年的枝同时萌发,当年生 的新枝则次年“休息”。这样,一株树木各个 年份的枝桠数,便构成斐波那契数列。这就是 图1 树木生长与斐波那契数列
斐波那契数列的通项公式推导 山西省原平市原平一中任所怀 做了这些年的数学题,我时常有这样的感受。一个新的数学题初次接触时,会觉得这个题的解题技巧很妙,甚至有点非夷所思,但如果把同类型问题多做几个,你就会发现原来所谓的技巧,其实是一种再正常不过的想法,是一种由已知到未知的必然之路。这样我们就由解题的技巧而转化到了通解通法,进一步就会形成解题的思想,所以我对于数学爱好者建议,做题时要把同类型题多种总结和分析,这样你的数学才会有长足的进步。 下面我们就由递推推导通项的问题,进行对比分析。 例1在数列中,,求数列的通项。(普通高中课程标准实验教科书人教A版必修5第69页6题) 分析:此题可分两步来进行,首先由构造一个等比数列,其中 ,并写出的通项;然后利用,两边同除以得 ,由累加法,就可求出数列的通项。 解:( 设,则()所以数列为等比数列,且首项为 ,公比为3。所以。 于是有,两边都除以得 设,则有 由累加法可得
因为所以() 于是有。 总结:上面的求解过程实质,求是一个把已知条件逐步化简的过程,由相邻三项的递推关系化为相邻两项的递推关系,进一步求出通项公式。 下面我们来研究一下著名的斐波那契数列的通项。 已知数列,其中,,求数列的通项。 解:首先我们要构造一个等比数列,于是设 则有。(1) 则由已知得(2) 对照(1)(2)两式得解得或。 我们取前一解,就会有。 设,则有 所以数列为等比数列,首项为,公比为
所以。即(3) 再次构造等比数列,设 则有 对照(3)式,可得所以 x=. 于是有 设,则有数列为等比数列,首项为,公比为,于是= 所以有。
一、选择题 1.一个.java文件中可以有()个public类。 A.一个B.两个C.多个D.零个 2.一个算法应该是() A.程序B.问题求解步骤的描述 C.要满足五个基本特性D.A和C 3.用计算机无法解决“打印所有素数”的问题,其原因是解决该问题的算法违背了算法特征中的()A.唯一性B.有穷性C.有0个或多个输入D.有输出 4.某校有6位学生参加学生会主席竞选,得票数依次为130,20,98,15,67,3。若采用冒泡排序算法对其进行排序,则完成第二遍时的结果是() A.3,15,130,20,98,67B.3,15,20,130,98,67 C.3,15,20,67,130,98 D.3,15,20,67,98,130 5.下列关于算法的描述,正确的是() A.一个算法的执行步骤可以是无限的B.一个完整的算法必须有输出 C.算法只能用流程图表示D.一个完整的算法至少有一个输入 6.Java Application源程序的主类是指包含有()方法的类。 A、main方法 B、toString方法 C、init方法 D、actionPerfromed方法 7.找出满足各位数字之和等于5的所有三位数可采用的算法思路是() A.分治法B.减治法C.蛮力法D.变治法 8.在编写Java Application程序时,若需要使用到标准输入输出语句,必须在程序的开头写上( )语句。 A、import java.awt.* ; B、import java.applet.Applet ; C、import java.io.* ; D、import java.awt.Graphics ; 9.计算某球队平均年龄的部分算法流程图如图所示,其中:c用来记录已输入球员的人数,sum用来计算有效数据之和,d用来存储从键盘输入的球员年龄值,输入0时表示输入结束。
斐波那契数列趣闻 目录 摘要 (1) 第一章斐波那契数列的提出 (2) 第二章斐波那契数列的应用 (2) 2.1 斐波那契数列与花朵的花瓣数 (2) 2.2 斐波那契数列与仙人掌的结构 (2) 2.3 斐波那契数列与向日葵种子排列方式 (3) 2.4 斐波那契数列与台阶问题 (3) 2.5 斐波那契数列与蜜蜂的家谱 (3) 2.6 斐波那契数列的其他应用 (3) 第三章黄金分割 (4) 第四章黄金分割的应用 (4) 4.1 黄金分割的美学应用 (4) 4.2 黄金分割在灾害科学中的应用 (5) 第五章总结 (5) 参考文献 (5) 摘要 自从斐波那契数列被提出以后,众多科学研究者对其产生了极大的兴趣,并由此导出了一些有趣的性质和结论,本文主要介绍与斐波那契数列的一些变式及其与自然、生活科学等方面的一些奇妙的联系,并谈及黄金分割率在生活中的应用。 关键字:斐波那契数列,黄金分割,应用 斐波那契数列是一个非常美丽、和谐的数列,它的形状可以用排成螺旋状的一系列正方形来说明,起始的正方形的边长为1,在它左边的那个正方形的边长也是1,在这两个正方形的上方再放一个正方形,其边长为2,以后顺次加上边长为3、5、8、13、2l……等等的正方形。这些数字每一个都等于前面两个数之和,它们正好构成了斐波那契数列。
第一章斐波那契数列的提出 意大利数学家斐波那契在《算盘全集》中提出了一个有趣的兔子繁殖问题:如果每队兔子(一雄一雌)每月能生殖一对小兔子(也是一雄一雌,下同)每队兔子第一个月没有生殖能力,但从第二个月以后便能每月生一对小兔子。假定这些兔子都不死亡现象,那么从一对刚出生的兔子开始,一年只有会有多少对兔子呢?解释说明为:一个月:只有一对兔子;第二个月:仍然只有一对兔子;第三个月:这对兔子生了一对小兔子,共有1+1=2对兔子。第四个月:最初的一对兔子又生一堆兔子,共成为2+1=3对兔子。后人为了纪念兔子繁殖问题的斐波纳契将这个兔子数列成为斐波那契数列。也就是把1,1,2,3,5,8,13,21,34…这样的数列称为斐波那契数列。 第二章斐波那契数列的应用 人类很早就从自然界中看到了数学特征:蜜蜂的繁殖规律,树的分枝,钢琴音阶的排列以及花瓣对称排列在花托边缘、整个花朵几乎完美无缺地呈现出辐射对称状……,所有这一切向我们展示了许多美丽的数学模式。而对这些自然、社会以及生活中的许多现象的解释,最后往往都能归结到Fibonacci数列上来。 斐波那契数列在数学理论上有许多有趣的性质,不可思议的是在自然界中也存在着这个性质,似乎完全没有秩序的植物的纸条彼此相隔的距离或叶子的生长凡是,都被斐波那契数列支持着。 2.1 斐波那契数列与花朵的花瓣数 花瓣数是极有特征的。多数情况下,花瓣的数目都是3,5,8,13,21,34,55,…这些数恰好是斐波那契数列的某些项,例如,百合花有3瓣花瓣,至良属的植物有5瓣花瓣;许多翠雀属植物有8瓣花瓣;万寿菊的花瓣有13瓣,更有趣的是,有一位学者细心地数过一朵花的花瓣,发现这朵花的花瓣刚好有157瓣。且他又发现其中有13瓣与其他144瓣有显著的不同,是特别长并卷曲向内,这表明这朵花的花瓣树木是由F1=13和F2=144合成的。 2.2 斐波那契数列与仙人掌的结构 在仙人掌的结构中有这一数列的特征。研究人员分析了仙人掌的形状、叶片厚度和一系列控制仙人掌情况的各种因素,并将所得数据输入电脑,结果发现仙人掌的Fibonacci数列结构特征能让仙人掌最大限度地减少能量消耗,适应其在
数学与几个生活实例的联系 一摘要 (1)概率论与日常生活 20世纪30年代科尔莫格罗夫提出概率公理化以来,概率论在生活的各个方面得到了广泛应用。 拉普拉斯名言———“生活中最重要的问题,绝大部分其实只是概率问题。” (2)数学与艺术 爱因斯坦说过:“这个世界可以由音乐和音符组成,也可以由数学的公式组成。” 古希腊数学家对音乐的认识开创了数学研究音乐的历史; 著名的黄金分割在音乐与数学上的应用。 (3)中国数学教育的缺陷 中国教育对于数学的不正确引导使得青年甚至儿童对于数学有了畏惧心理与抗拒心理。功利化的考查制度也让真正对于数学感兴趣的人部分或者完全丧失了学习数学的动力与兴趣。 43A13418 张弘毅
二正文 第一章概率论与日常生活 “要成为现代社会中有文化的人,必须对博弈论有大致的了解”——著名经济学家萨缪尔森 中世纪欧洲盛行掷骰子赌博,帕斯卡,费马与旅居巴黎的荷兰数学家惠更斯用组合数学研究了许多于掷骰子有关的概率问题。20世纪30年代科尔莫格罗夫提出概率公理化以来,概率论在生活的各个方面得到了广泛应用。 由于本人水平有限,对于概率论无研究,只能简单举例并粗略计算 (1)纽约乐透一人中两次头奖 就单次来说,中头奖概率是1/22500000,那么按照常识,一人中两次概率为1/506250000000000 但是单纯的平方计算没有考虑到开奖次数的问题。每年开奖104次,15年大约1500次开奖。所谓的赌徒心理会让中过奖的人继续买彩票,每次总注数超过3000注。15年内再次中奖概率则大于五分之一,所以连中头奖才是真正的小概率事件。十几年内如果中两次头奖,从概率角度则不算太稀奇。 (2)概率学分析华南虎造假事件 2007年陕西省林业厅声称发现华南虎并提供照片。照片与年画极其相似,经过鉴定,相似率高达99% 概率学上来说,由于华南虎所处环境,动作神态每时每刻都会发生变化,与年画如此相似的概率无限趋近0 (3)综述 由以上两个例子可以看出,生活中从与普通民众相关的彩票博弈到鉴别照片真伪等问题都有概率学的影子。如今的初中,高中考试等等都会有类似问题提出。本人是江苏毕业生,清楚的记得江苏高考中附加题的最后一题常常是概率问题,在各种附加条件之下求出事件发生概率。其中要多次用到排列组合,对于逻辑思维能力有很高的要求。但是概况论面向普通民众推广时则极为便利。从彩票股票,赌博跑马(当然还有学生蒙答案也会用到概率)到天气预报,灾害预警等等与生活息息相关的方面都用到概率学原理。但是对于真正的概率学研究来说又是没有很大的促进作用,但是能调动群众的积极性这点还是有着重要意义。总结一下,概率学,上手容易,精通难;推广容易研究难。
浅谈斐波那契数列在生活中的应用 发表时间:2019-07-29T11:38:49.093Z 来源:《基层建设》2019年第14期作者:孙烨赵倩[导读] 摘要:数学是一门来自生活又高于生活的科学,数学研究是人类社会进步的动力。 山东协和学院山东济南 250107摘要:数学是一门来自生活又高于生活的科学,数学研究是人类社会进步的动力。数列知识在生活中也有着广泛的应用,例如生物种群数量的变化,银行的利息计算,人口增长,粮食增长、住房建设等,都会用到数学知识。本文介绍斐波那契数列的简单情况,可以帮助学生提高对数列的知识。数列是数学学习中一个非常重要的分支,并且因为数列的研究和计算与社会经济和资源生活紧密相关,加上灵活 多变的计算,有趣的问题等,都使得对于数列的研究受到越来越多人的关注。 关键词:斐波那契数列应用黄金分割 1 引言 数列在我们的生活中具有广泛的应用,例如资源计算等问题,并且在解决诸如投资分配,汇率计算和资源利用分配等问题方面具有无可比拟的优势。本文将简要介绍数列广泛应用,分析斐波那契数在上述几个生活领域中的应用。 斐波那契数列在现实生活中被广泛使用,研究它以使其服务于我们的生活具有很大的意义。 人类很早就看到了大自然的数学特征:蜜蜂的繁殖规律,树枝、钢琴音阶的排列以及花瓣在花托边缘的对称分布、整个花朵几乎完美无缺地呈现出辐射对称性……,所有这一切向我们展示了许多美丽的数学模式。对自然、社会和生活中的许多现象的解释,通常可归因于斐波那契数列上来。 斐波那契数列在数学理论中有许多有趣的特性,似乎在自然界中也存在着这个性质,都被斐波那契数列支持。 2 斐波那契数列的应用 (1)斐波那契数列和花瓣数花瓣数是极有特征的。多数情况下,花瓣的数目都是3,5,8,13,21,34,55,…这些数恰好是斐波那契数列的某些项,例如,海棠2瓣花瓣,铁栏、百合花和兰花以及茉莉花都有3瓣花瓣,洋紫荆、黄蝉和蝴蝶兰是5瓣花瓣。万寿菊的花瓣有13瓣;至良属的植物有5瓣花瓣;许多翠雀属植物有8瓣花瓣;雏菊属植物有89、55或者34个瓣花瓣。 (2)斐波那契数列和仙人掌的结构在仙人掌的结构中有这一数列的特征。研究人员分析了仙人掌的形状、叶片的厚度以及控制仙人掌情况的其他因素,并将数据输入计算机,结果发现仙人掌的斐波那契序列结构使仙人掌能够最大限度地减少能量消耗并适应干旱沙漠中的生长环境。 (3)斐波那契数列和向日葵种子排列向日葵种子的排列是典型的数学模型。仔细观察向日葵盘,你会发现两组螺旋,一组顺时针旋转,另一组螺旋逆时针旋转,彼此嵌套。虽然不同向日葵品种的种子选装方向和螺旋线的数量有所不同,但往往不会超出34和55、55和89或者89和144这3组数字,每组数字就是斐波那契序列中的两个相邻数字。前一个数字是顺时针旋转的线数,后一个数字是逆时针旋转的线数。回想起向日葵。种子全都紧密排列在花盘当中,每个种子都保证按照适合的角度生长大小还基本保持一致又疏密得当,与此同时,螺旋的数目也是斐波那契序列中的数字,世界如此繁琐,却又如此的井然有序。 (4)斐波那契数列与台阶问题当只有一个台阶时,只有一种移动方式,F1=1两个台阶,有2种走法,一步上两个台阶或者一阶一阶的上,所以F2=2。三个台阶时,走法有一步一阶,2阶再1阶,1阶再2阶,因此,F3=3。四个台阶时,走法有(1,1,1,1),(1,1,2),(1,2,1),(2,1,1)(0,2,2),共5种方法,所以F4=5依此类推,有数列:1,2,3,5,8,13,21,34,55,89,144,233,...斐波那契与自然,生活和科学上有很多联系,但是从这几个例子中,我们可以看到斐波那契数列的应用的广泛性,我们可以看到数学之美无处不在。它是一门科学,同时也是一种艺术,一种语言,它就像一朵盛开的茉莉花,白皙而优雅,简言而之,数学伴随着自然生活共同发展。 (5)斐波那契数列与蜜蜂的家谱蜜蜂的“家谱”:蜜蜂的繁殖规律十分有趣。雄蜂只有一个母亲,没有父亲,因为蜂后所产的卵,未受精的孵化为雄蜂,受精的孵化为雌蜂(即工蜂或蜂后)。人们在追踪雄蜂的家谱时,发现1只雄蜂的第n代子孙的数目刚好就是斐波那契数列的第n项f(n)。 (6)黄金分割与斐波那契的联系斐波那契和黄金比例(也称黄金分割,Φ,取三位小数1.618)密切相关。黄金法则,也称为黄金比率,是指将直线分成两部分,使得一部分与整体的比率等于剩余部分与该部分的比率,即0.618/1=0.382/0.618。0.618是斐波那契数列相邻两项之比的近似值,一般称之为黄金分割数。这是古希腊哲学家、数学家毕达哥拉斯于公元前6世纪由提出,后被著名的希腊美学家柏拉图称为“黄金比例率”。 (7)斐波那契数列和鳞片的关系菠萝果实上的菱形鳞片排成一列,8排向左倾斜,13排向右倾斜;挪威云杉的球果在一个方向上有3排鳞片,在另一个方向上有5排鳞片;常见的落叶松是一种针叶树,松果上有鳞片,两个方向也排成5行8行;美国松树松鳞片在两个方向上排成3行和5行。 (8)影视作品中的斐波那契数列斐波那契数列在欧美可以说是是每个人都知道,在电影这种通俗艺术中也经常的出现,例如在风靡一时的《达芬奇密码》当中它就作为一个重要的符号和情节线索出现,在《魔法玩具城》当中也出现过。由此可见此数列就像黄金分割那样的流行。可是虽说叫得上名,大多数人并没有深入理解研究。在电视剧中也经常看到斐波那契数列的影子,比如:日剧《考试之神》的第五回,义嗣做全国模拟考试题中的最后一道数学题。还在FOX热播美剧《Fringe》中也是多次引用,甚至被当做全剧宣传海报的主要设计元素。 3 结束语 除了上文中涉及的几个方面外,斐波那契数列在生活的其他领域当中例如现代物理、准晶体结构、化学等领域,斐波纳契数列都有着广泛的应用。这个奥秘神奇的序列就在我们生活中任何常见的事物中隐藏,植被如一朵向日葵,一棵花菜,宏观如飓风以及星系,微观小至细胞的分裂,斐波那契数列都有存在。而且,通过对上文数列在生活中应用的几个方面的分析,也希望能激发大家对斐波那契数列的兴趣,感受数学的魅力。
详解由递推公式求斐波那契数列的通项公式 武汉市黄陂区第四中学 蔡从江 斐波那契数列的递推公式是121==a a ,11-++=n n n a a a (2≥n 且N n ∈),那么它的通项公式是怎样的呢?不少同学经常问到这个问题。 下面详细解答用待定系数法构造过渡数列求其通项公式。 由递推公式11-++=n n n a a a ,可设)(11-++=+n n n n a a a a λμλ,比较得1=-λμ且1=μλ,即012=-+λλ,解得251±-= λ。若251+-=λ,则251+=μ;若251--=λ,则2 51-=μ。 先以2 51+-=λ,251+=μ求解, 此时)2)(2 15(21521511≥-++=-+-+n a a a a n n n n , 所以)2()215()215()215(2151211≥+=-++=-+ -+n a a a a n n n n , 即)2()2 15(2511≥++-=+n a a n n n , 再另)2]()215([251)215( 11≥+--=+-++n x a x a n n n n 即n n n x x )2 15()215(215)215(1+=+-+++, 所以12 15215=-++x x 即55=x , 所以 ])215(55[251)215(5511n n n n a a +--=+-++, )2]()2 15(551[)251()215(552111≥+--=+--++n a n n n ,
所以)2]()2 15(551[)251()215(552111≥+--=+--++n a n n n , )2]()251()251[(5 1])215(551[)251()215(55112111≥--+=+--++=++-++n a n n n n n 所以)3]()251()251[(5 1≥--+=n a n n n , 又121==a a 适合上式,故 *)]()251()251[(51N n a n n n ∈--+=, 同理可得251--=λ,2 51-=μ时,*)]()251()251[(51N n a n n n ∈--+=, 因此斐波那契数列的通项公式是 *)]()251()251[(51N n a n n n ∈--+=
浅谈菲波纳契数列的内涵和应用价值 99数学本四班 莫少勇 指导教师 孙丽英 摘 要 本文从菲波那契数列出发,通过探究其数学内涵和它在实际生活中的应用,提高学生对数学的欣赏能力,初步建立数学建模的思想,从而提高用数学知识分析实际问题的能力。 关键词 Fibonacci 数列 黄金数 优选法 数学美不仅有形式的和谐美,而且有内容的严谨美;不仅有语言的简明、精巧美,而且有公式、定理的结构整体美;不仅有逻辑、抽象美,而且有创造应用美。古希腊的毕达哥拉斯学派,首先从数的比例中求出美的形式,发现了黄金数。神奇的菲波纳契数列正是黄金数之后的一大发现,它又被誉为“黄金数列”。 一. F ibonacci 数列的由来 Fibonacci 数列的提出,当时是和兔子的繁殖问题有关的,它是一个很重要的数学模型。这个问题是:有小兔一对,若第二个月它们成年,第三个月生下小兔一对,以后每月生产一对小兔,而所生小兔亦在第二个月成年,第三个月生产另一对小兔,以后亦每月生产小兔一对,假定每产一对小兔必为一雌一雄,且均无死亡,试问一年后共有小兔几对? 对于n=1,2,……,令F n 表示第n 个月开始时兔子的总对数,B n 、A n 分别是未成年和成年的兔子(简称小兔和大兔)的对数,则F n = A n +B n 根据题设,有 显然,F 1=1,F 2=1,而且从第三个月开始,每月的兔子总数恰好等于它前面两个月的兔子总数之和,于是按此规律我们得到一个带有初值的递推关系式: ?? ?==∈≥+=1 F 1,F Z)n 3,(n F F F 212-n 1-n n 若我们规定F 0=1,则上式可变为 ?? ?==∈≥+=1F 1,F Z)n 2,(n F F F 102-n 1-n n 这就是Fibonacci 数列的通常定义,也就是数列1,1,2,3,5,8,13,21,34,55,89,……, 这串数列的特点是:其中任一个数都是前两数之和。 这个兔子问题是意大利数学家梁拿多(Leomardo )在他所著的《算盘全集》中提出的,而梁拿多又名菲波纳契(Fibonacci ),所以这个数列称作菲波纳契数列,其中每一项称作Fibonacci 数。 它的通项是F n =51[(25 1+)n+1-(251-)n+1 ],由法国数学家比内(Binet )求出的。 二.Fibonacci 数列的内涵 (1)Fibonacci 数列的通项的证明我们可以通过求解常系数线性齐次递推关系或者利用生成函数法来实现。 证法一:
斐波那契数列 斐波那契数列,又称黄金分割数列、因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。 定义 斐波那契数列指的是这样一个数列1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368........ 自然中的斐波那契数列 这个数列从第3项开始,每一项都等于前两项之和。 斐波那契数列的定义者,是意大利数学家列昂纳多·斐波那契,生于公元1170年,卒于1250年,籍贯是比萨。他被人称作“比萨的列昂纳多”。1202年,他撰写了《算盘全书》(Liber Abacci)一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点于阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。 通项公式 递推公式 斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... 如果设F(n)为该数列的第n项(n∈N*),那么这句话可以写成如下形式::F(n)=F(n-1)+F(n-2) 显然这是一个线性递推数列。 通项公式
Xxxxxxxxxxx大学 课程论文(2013-2014学年春季学期) 论文题目: 课程名称: 任课教师: 班级: 学号: 姓名:
浅谈斐波那契数列 摘要: 斐波那契数列,又称作黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21……这个数列从第三项开始,每一项都等于前两项之和。斐波那契数列的发明者,是意大利数学家列昂纳多?斐波那契(Leonardo Fibonacci)。本文主要就斐波那契数列的提出与特征进行简要分析,通过举例重点说明斐波那契数列在实际生活当中的表现与应用,进而得到启示。 关键词: 斐波那契数列; 特征; 应用 Research on Fibonacci sequence (Institute of Technology, China Agricultural University, FENG-Wei) Abstract: Fibonacci sequence, also known as the golden series, referring to such a sequence: 1,1,2,3,5,8,13,21…… this sequence beginning from the third term, each of which equal to the sum of the first two terms. The inventor of Fibonacci series was an Italian mathematician——Leonardo Fibonacci. This tractate focuses on the characteristics of Fibonacci sequence and has a brief analysis, as well as giving examples to analyze the performance and application of Fibonacci sequence in real life, and then get inspirations. Key words: Fibonacci sequence; Characteristics; Application
斐波那契数列说课稿 【教材的地位、作用分析】 本节课的内容选自人教社《必修5》第二章“数列”中的章头图和阅读思考材料,是在学习了数列的基本概念的基础上,对数列问题的进一步研究和拓展。设计说明: 大家请看,这是数列单元的章头图,以向日葵的花冠、树木的分杈、花瓣的数量等自然现象遵循斐波那契数列来让学生感受大自然的丰富多彩,体会“大自然是懂数学的”。 阅读材料中则详细介绍了斐波那契数列的由来和定义,进一步阐述了章头图中提出的斐波那契数列在植物界中的应用,鼓励有兴趣的同学搜集资料,深入了解和研究斐波那契数列。 课本中安排的章头图和阅读思考材料贴近学生的生活实际,具有趣味性、科学性、实用性等功能,是教材不可分割的一部分,也是教师对教材进行二次开发的有效素材,因而不能被淡化或忽视,应该充分发挥它的教育功能。
【教学模式、课型分析】 本节课的课型定位为数学项目活动课。 由教师结合课本引入斐波那契数列这一数学知识,指导学生利用课余时间自主探究斐波那契数列在各领域中的应用,最后以小组汇报的形式将研究成果向同学和老师们展示。 真正做到以教师为主导,学生为主体,将课堂和数学学习的主动权交给学生。设计说明:我国新课程改革的目标特别强调有效的数学学习应该重视开展独立而积极的数学活动,让学生通过动手实践、自主探索与合作交流来学习数学,获得广泛的数学活动经验。 数学项目活动学习这一类型的数学课是帮助活动参与者达到上述目的的有效手段。在国外已有广泛的普及,在国内尚处于起步阶段。本人在高一年级选取了斐波那契数列这一古老的数学问题,开展数学项目活动学习,是对新课程改革的一种尝试。 【学情分析】 从学生已有的认知基础来看,学生刚刚接触数列这一新知识,初步掌握了数列的基本概念。 在进一步学习数列知识之前引入斐波那契数列的研究性课题,可以使学生在接下来的数列学习中带着问题去学,更具针对性和发展性。 特别是在学习完数列整个章节后,再用数列知识解释现实生活中的问题,有助于深化学生对数列知识的认识,从而进一步提升数学素养和水平。 从能力基础看,学生具有较强的信息技术能力和广博的见识,完
实验二Linux 进程创建 实验目的 ?加深对进程概念的理解 ?练习使用fork()系统调用创建进程 ?练习Linux操作系统下C程序设计 实验准备知识 1. fork()函数:创建一个新进程. ?调用格式: #include
输出。在退出程序之前,父进程调用wait()等待子进程完成。 要求提供必要的错误检测以保证在命令行传递的参数是非负数. 实验程序: #include
有趣的斐波那契数列 谈起斐波那契数列,我想很多人会想到《达芬奇密码》中的故事:午夜,卢浮宫博物馆年迈的馆长被人杀害在大陈列馆的镶木地板上.在人生的最后时刻,馆长脱光了衣服,明白无误的用自己的身体摆成了达.芬奇名画维特鲁维人的样子,还在尸体旁边留下了一个令人难以捉摸的密码.符号学专家罗伯特.兰登与密码破译天才索菲.奈夫,在对一大堆怪异的密码进行整理的过程当中,发现一连串的线索竟然隐藏在达.芬奇的艺术作品当中。而这串密码就是斐波那契数列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... 然而它们到底是怎样的一串数字呢?今天就让我们一起来认识一下吧!斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*) 递推公式 斐波那契数列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, (1) 如果设F(n)为该数列的第n项(n∈N*),那么这句话可以写成如下形式:[1] 显然这是一个线性递推数列。[1] 通项公式 (如上,又称为“比内公式”,是用无理数表示有理数的一个范例。) 注:此时a1=1,a2=1,an=a(n-1)+a(n-2)(n>=3,n∈N*) 待定系数法构造等比数列2(初等代数解法) 已知a1=1,a2=1,an=a(n-1)+a(n-2)(n>=3),求数列{an}的通项公式。 解:设an-αa(n-1)=β(a(n-1)-αa(n-2))。 得α+β=1。 αβ=-1。 构造方程x^2-x-1=0,解得α=(1-√5)/2,β=(1+√5)/2或α=(1+√5)/2,β=(1-√5)/2。 所以。 an-(1-√5)/2*a(n-1)=(1+√5)/2*(a(n-1)-(1-√5)/2*a(n-2))=[(1+√5)/2]^ (n-2)*(a2-(1-√5)/2*a1)`````````1。 an-(1+√5)/2*a(n-1)=(1-√5)/2*(a(n-1)-(1+√5)/2*a(n-2))=[(1-√5)/2]^ (n-2)*(a2-(1+√5)/2*a1)`````````2。 由式1,式2,可得。
用初等数学方法求斐波那契数列的通项公式 斐波那契 (Fibonacci) 数列是着名的数列,有很高的实用价值。多年来,学者们一直在探究它的通项公式的求解方法,已经涌现出了多种方法。但据笔者们所知,这些方法大都需要比较高深的数学知识,例如组合数学的方法、概率的方等等,让人比较难理解,不容易接受。基于此,研究给出了一种简易的初等数学方法,先探求它们的特征多项式,然后通过求解线性方程组的思想,得出它们的通项公式。这种方法深入浅出,有一定的实用价值。 1.斐波那契数列的由来 13 世纪意大利数学家斐波那契在他的《算盘书》的修订版中增加了一道着名的兔子繁殖问题. 问题是这样的: 如果每对兔子(一雄一雌)每月能生殖一对小兔子(也是一雄一雌,下同),每对兔子第一个月没有生殖能力,但从第二个月以后便能每月生一对小兔子.假定这些兔子都没有死亡现象,那么从第一对刚出生的兔子开始,12 个月以后会有多少对兔子呢解释说明为:一个月:只有一对兔子;第二个月:仍然只有一对兔子;第三个月:这对兔子生了一对小兔子,共有1+1=2 对兔子.第四个月:最初的一对兔子又生一对兔子,共有2+1=3对兔子.则由第一个月到第十二个月兔子的对数分别是:1,1,2,3,5,8,13,21,34,55,89,144,……,人为了纪念提出兔子繁殖问题的斐波纳契,将这个兔子数列称为斐波那契数列,即把 1,1,2,3,5,8,13,21,34…这样的数列称为斐波那契数列。 2.斐波那契数列的定义 定义:数列F1,F2,… ,Fn,…如果满足条件121==F F ,21--+=n n n F F F (对所有的正整数n ≥ 3),则称此数列为斐波那契(Fibonacci)数列。
黄金螺旋线教学设计 一、教学背景分析 1.教材分析: 新北京版教材经教育部审定后于2014年下半年开始正式使用。而《黄金螺旋线》则是新教材在六年级上学期首次加入的教学内容。教材呈现上是先介绍鹦鹉螺旋线,再通过对螺旋线画法的研究发现扇形半径所组成的数列规律,也就是著名的斐波那契数列。我们从教材的呈现可以看出:首先教材对学生的要求不高,只要能在螺旋线中发现半径的长度所组成数列的简单规律(从第三项起后一项等于前两项数字之和)就可以了。其次,教材为学生留下了广阔的探索空间,我们可以想象如果学生单单学习教材他们必然会产生一些问题。比如这个数列有没有名字?数列还有什么其他特点?学习黄金螺旋线有什么用……而这节课上就可以让学生把这些质疑解开。学生在展示自己的发现并在汇报中进一步帮助学生积累数学活动经验和数学思想方法。 2.学情分析: 这是一节新课,但书上内容对于六年级的学生来说并不难,学生对于实践活动课的热情很高。在学过的知识中,找数列规律对于学生们来说并不困难,只要把小扇形的半径仔细观察就会得出规律。所以根据学生的学习特点,我并没有把找斐波那契数列的特点作为重点,而是在此基础上拓宽学生思维,让学生们探寻这个数列其他特殊之处。另外学生在感受到这种美后,自然的想有亲自创造美的思想火花。最后孩子们经历了画斐波那契数列的时候真正做到了培养和锻炼了孩子的能力。 二、教学目标和重难点。 1、通过学生填表讨论,初步了解斐波那契数列的简单规律认识到斐波那契数列与鹦鹉螺旋线之间存在关系,发展学生学习数学的兴趣。 2、在汇报过程中进一步理解斐波那契数列,体会其与鹦鹉螺旋线的关系。发展学生观察、分析、推理、归纳的能力。帮助学生积累数学活动经验和数学思想方法。 3、在绘制黄金螺旋线的过程中,提升学生欣赏数学美、创造数学美的能力。 教学重点:进一步理解斐波那契数列,体会其与黄金螺旋线的关系。 教学难点:利用斐波那契数列与黄金螺旋线之间的关系绘制黄金螺旋线。 三、教学过程 (一)导入新课