勾股定理
中考考点
掌握勾股定理的内容，能利用勾股定理进行计算与证明。
考点讲解
勾股定理：直角三角形两直角边的平方和等于斜边的平方。即：c2=a2+b2(c为斜边)。
它反映了直角三角形三边之间的数量关系，是解决直角三角形中计算问题以及解直角三角
形的主要依据之一。
一、问题的提出：
小明放学回家要经过一块长方形的麦地。如图：
1、小明本来应走大路从A经B到C可是他却直接从
A到C，为什么？
2、为什么近、近多少？
3、用数学知识如何解答？
二、量一量，算一算：
1、直角三角形的两条直角边的长度分别为3㎝，4㎝和5㎝，12㎝请你量出斜边的长度。
2、进行有关的计算。
3、得出结论：
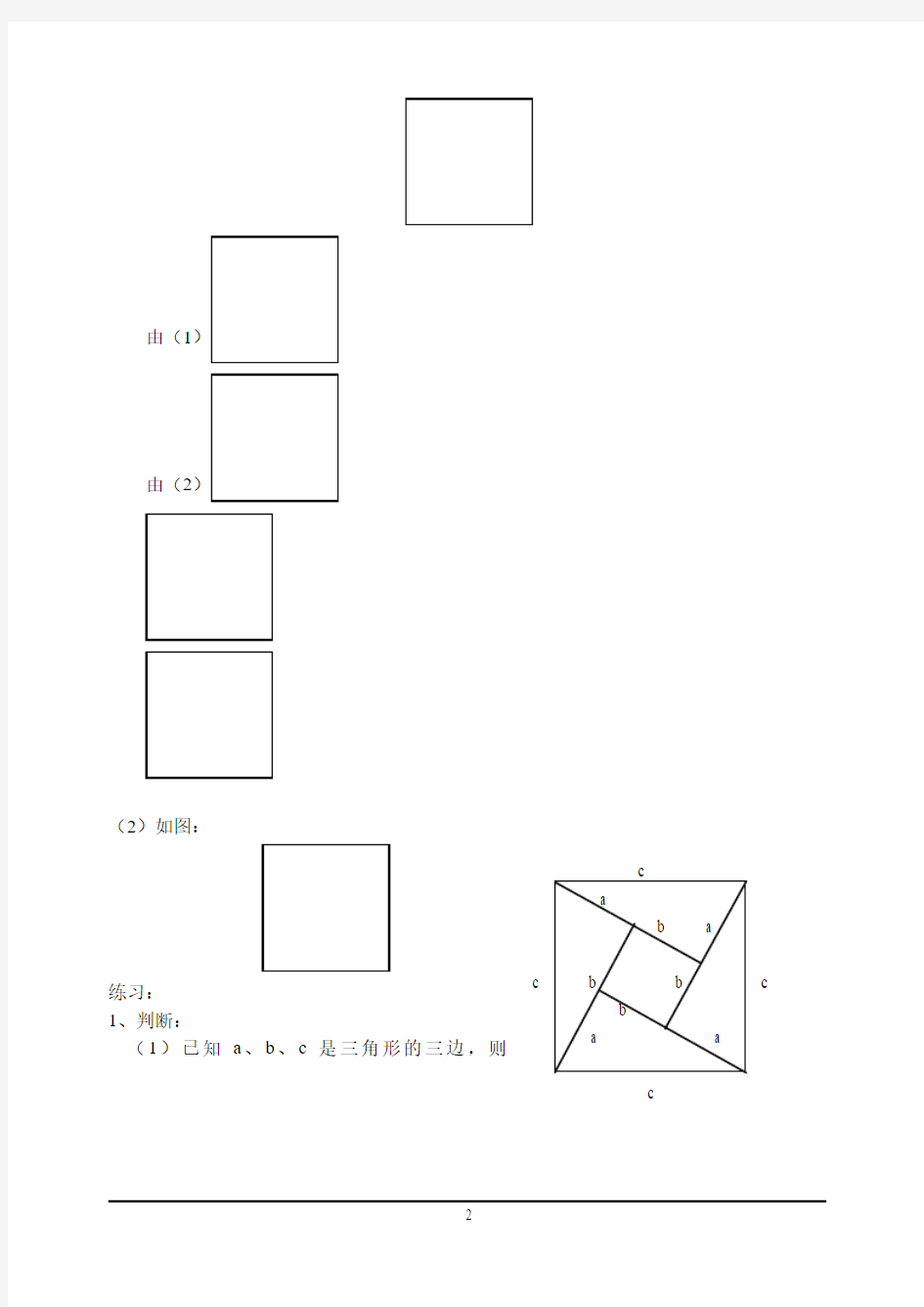
三、证明结论：
利用拼合三角形的方法，如下：（1）A
B
C
D 3cm
6cm
8cm
由（1
由（2
（2）如图：
练习：
1、判断：
（1）已知a、b、c是三角形的三边，则
c
a
b a
c b b c
b
a a
c
（ ）
（2）在直角三角形中两边的平方和等于第三边的平方。 （ ）
（3 90=B
（ ）
2（1）如果a=3，b=4，则c= （2）如果a=6，b=8，则c= （3）如果a=5，b=12，则c= (4) 如果a=15，b=20，则c= 3、 解决新课开始提出的问题 中考考点 1．把握勾股定理的逆定理；
2，用勾股定理的逆定理判定一个三角形是不是直角三角形。
考点讲解
1．勾股定理的逆定理：如果三角形的三边长a 、b 、c 有下面关系：
a 2
+b 2
= c 2
，那么这个三角形是直角三角形。
注意：勾股定理是直角三角形的性质定理，而勾股定理的逆定理是直角三角形的判定
定理。 1．用勾股定理的逆定理判定一个三角形是否是直角三角形的步骤： （1）首先求出最大边（如c ）；
（2）验证a 2
+b 2
与c 2
是否具有相等关系；
若c 2=a 2+b 2，则△ABC 是以∠C=90°的直角三角形。 若c 2 ≠a 2+b 2，则△ABC 不是直角三角形。
2．直角三角形的判定方法小结：
（1）三角形中有两个角互余； （2）勾股定理的逆定理；
3．紧记一些常用的勾股数，将为我们应用勾股定理逆定理带来方便，如3、4、5；5、
12、13；6、8、10；12、16、20等。
四、典型例题
例1.
D ，求证：
（1
（2
分析：
以求证。 证明：
（1
C
A D B
（2
例2、
AC
边上的高线的长。
分析：首先通过所给的三角形的三边长，判断出所求高线长的三角形为直角三角形，并且要求的为斜边上的高线，通过勾股定理可解，未知量可用方程的思想求得。
B
12 5
C 13
D A
D
答：AC
例3.已知：如图，△ABC 中，AB =AC ，D 为BC 上任一点，
求证：AB 2－AD 2=BD ·DC
思路分析：通常遇到等腰三角形问题，都是作底边上的高转化为直角三角形，再按解直角三角形的思路探索。本例首先作AE ⊥BC 于E ，便出现两个全等的直角三角形。
由AB ==EC
结论又以平方差“面目”出现，也就告知我们应用勾股定理是打开思路的好方法，那么在Rt △ABE ，Rt △ADE 中，由勾股定理，得
由于BE 、DE 均在一条直线BC 上，通常是平方差公式进行因式分解，转化为求同一条线段的和差问题，使结论明朗化，于是 AB 2－AD 2=(BE +DE )(BE －DE ) 结合图形知：BE +DE =BD BE －DE =CE －DE =CD
例4.如图，已知四边形ABCD 的四边
DA 的长分别为3、4、13、12，∠CBA =90°,求S 四边形ABCD 思路分析：遇到四边形，通常是连对角线转化为三角形问题，对本例连对角线AC 为佳，因∠CBA =90°，便出现了直角三角形ABC ，由勾股定理可求
AC 2=AB 2+BC 2=32+42=25
在△CAD 中，我们又可发现： AC 2+AD 2=25+122=169 DC 2=132=169
∴AC 2+AD 2=CD 2，由勾股定理逆定理知 ∴△ACD 为Rt △，且∠DAC =90°
此时，已清晰可知，这个四边形由两个直角三角形构成，求其面积便容易了。
S 四边形ABCD =S △ABC +S △ACD
例5、在正方形ABCD 中, F 为DC 的中点, E 为BC 上一点, 且
EC 求证: ∠EF A = 90︒
分析: 通过图形结构和求证本题思路十分明显, 就是要找那就是
要通过勾股定理逆定理来完成。 证明: 设正方形ABCD 的边长为4a 则EC = a , BE = 3a , CF = DF = 2a
在
在
在
为且AE是最大边, 即∠AFE = 90︒
例6、已知：如图，在正方形ABCD中，E，F分别AB，AD上的点，又AB=12，
EF=10，△AEF的面积等于五边形EBCDF AE，AF
的长。
思路分析：依题意知△AEF为Rt△用勾股定理，立马而定，于是有
EF2=AE2+AF2
设AE=x,AF=y,又EF2=100,则x2+y2=100 ①
