
面面垂直测试题
1.如图,ABCD 是正方形,O 是正方形的中心,PO 底面ABCD ,E 是PC 的中点。
2.如图,在三棱锥中,,平面,,分别为,的
中点.
(1)求证:平面;
(2)求证:平面平面.
3如图在三棱锥中,分别为棱的中点,已知
,
求证(1)直线平面;
(2)平面平面.
4.如图,在四棱锥中,底面是正方形,侧面底面.
(Ⅰ)若,分别为,中点,求证:∥平面;
(Ⅱ)求证:;
(Ⅲ)若,求证:平面平面.
,,PC AC AB ,,D E F -P ABC F E
D A
C B P
PCD PAB ⊥22
PA PD AD ==CD PA ⊥PAD EF BD PC F E ABCD PAD ⊥ABCD P ABCD -F
E
A
C P
B AB
C ⊥BDE DEF //PA ,6,8,5PA AC PA BC DF ⊥===PAB AEF ⊥ABC //EF PC PB F E
ABC PA ⊥90ABC ∠=P ABC -⊥求证:(1)PA ∥平面BDE
(2)平面PAC ⊥平面BDE
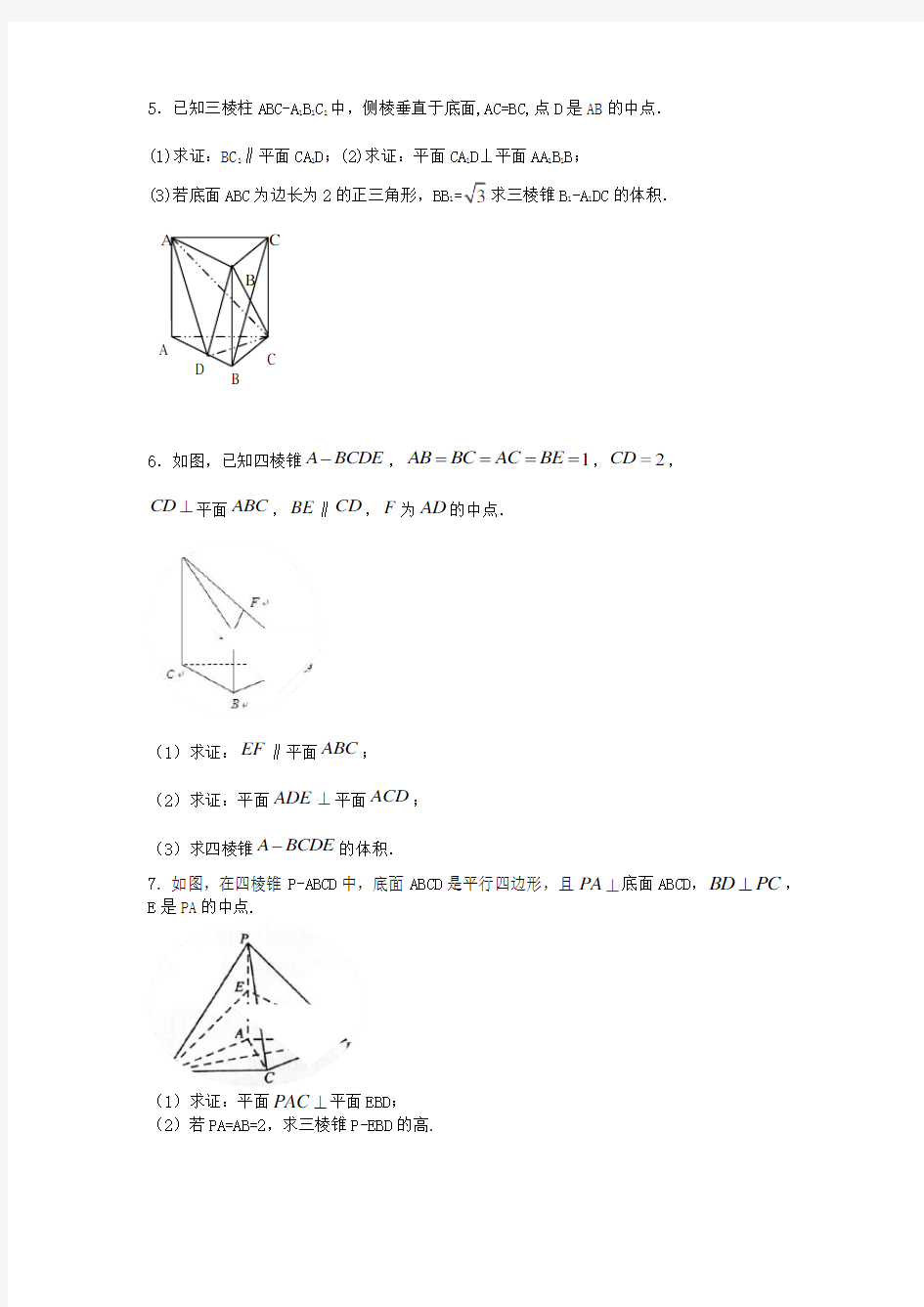
5.已知三棱柱ABC-A 1B 1C 1中,侧棱垂直于底面,AC=BC,点D 是AB 的中点.
(1)求证:BC 1∥平面CA 1D ;(2)求证:平面CA 1D⊥平面AA 1B 1B ;
(3)若底面ABC 为边长为2的正三角形,BB 1=
求三棱锥B 1
-A 1DC 的体积.
6.如图,已知四棱锥,,,
平面,∥,为的中点.
(1)求证:∥平面;
(2)求证:平面平面;
(3)求四棱锥的体积.
7.如图,在四棱锥P-ABCD 中,底面ABCD 是平行四边形,且底面ABCD ,,
E 是PA 的中点.
(1)求证:平面平面EBD ;
(2)若PA=AB=2,求三棱锥P-EBD 的高.
A
D
B C C
A
B 3PA
C ⊥B
D PC ⊥PA ⊥A BCD
E -ACD ⊥ADE ABC E
F AD F CD BE ABC CD ⊥2CD =1AB BC AC BE ====A BCDE -
面面垂直测试题
1.证明:(1)∵O 是AC 的中点,E 是PC 的中点,∴OE ∥AP ,
又∵OE 平面BDE ,PA 平面BDE ,∴PA ∥平面BDE
(2)∵PO 底ABCD,∴PO BD ,又∵AC BD ,且AC PO=O
∴BD 平面PAC ,而BD 平面BDE ,∴平面PAC 平面BDE
2.证明:(1)在中,分别为的中点 3分
又平面,平面平面 7分
(2)由条件,平面,平面
,即, 10分
由,,
又,都在平面内 平面
又平面平面平面
3.(1)由于分别是的中点,则有,又,
,所以.
(2)由(1),又,所以,又是中点,所以
,,又,所以,所以,是平面内两条相交直线,
所以,又,所以平面平面.
4.(3)(Ⅲ)在△中,因为, 所以. 由(Ⅱ)可知,且,所以平面.
又因为平面,所以平面平面
5.由(Ⅱ)可知,且,所以平面.又因为平面,
所以平面平面.
证明(1)连接AC 1交A 1C 于点E ,连接DE
因为四边形AA 1C 1C 是矩形,则E 为AC 1的中点
又D 是AB 的中点,DE∥B C 1,
又DE 面CA 1D ,BC 1面CA 1D ,BC 1∥面CA 1 (4分)
证明(2)AC=BC ,D 是AB 的中点,AB⊥CD,
又AA 1⊥面ABC ,CD 面ABC ,AA 1⊥CD,
AA 1∩AB=A,CD⊥面AA 1B 1B ,CD 面CA 1D ,
平面CA 1D⊥平面AA 1B 1B (8分)
(3)解:,则(2)知CD⊥面ABB 1B ,所以高就是CD=,BD=1,BB 1=,
PCD PAB ⊥PAB PA ?PCD PA ⊥=CD PD D CD PA ⊥PA PD ⊥22PA PD AD ==
PAD 331111B A DC C A B D V V --=????PCD PAB ⊥PAB PA ?PCD PA ⊥=CD PD D CD PA ⊥ABC ⊥BDE BDE DE ?平面DE ABC ⊥平面ABC ,EF AC DE EF ⊥222
DE EF DF +=5DF =142EF BC ==132DE PA ==AB F PE AC ⊥PA AC ⊥//PA DE //PA DEF 平面DE DEF ?平面PA DEF ?平面//PA DE ,PC AC ,D E PAB ⊥AEF ∴AEF ?EF PAB ⊥EF ∴PAB AB PA ,A AB PA =?EF PA ⊥EF AB ⊥∴//EF BC BC AB ⊥?=∠90ABC BC PA ⊥∴ABC ?BC ABC ⊥PA ABC //EF ∴ABC ?EF ABC ?BC BC EF //∴PC PB ,F E , PBC ???⊥ABCD BD 面?⊥⊥ ⊥?⊥
所以A 1D=B 1D=A 1B 1=2,, (12分) 6.解:(1)取中点,连结,,分别是,的中点, ∥,且.
∥, 与平行且相等.
所以四边形为平行四边形,∥. 3分
又平面,平面.∥平面. 4分
(2)为等边三角形,为的中点,. 又平面,平面., 6‘ 又,平面. 7分
∥,平面, 8分
平面,平面平面. 10分
(3)取中点,连结., .
平面,平面 ,
又, 平面,
是四棱锥的高,且, 12分 .
7(1)因为PA ⊥平面ABCD ,所以PA ⊥BD .又BD ⊥PC ,所以BD ⊥平面PAC ,
因为BD ?平面EBD ,所以平面PAC ⊥平面EBD . 5分
(2)由(1)可知,BD ⊥AC ,所以ABCD 是菱形,∠BAD =120?.
所以. 7分 设AC ∩BD =O ,连结OE ,则(1)可知,BD ⊥OE . 所以.
设三棱锥P -EBD 的高为h ,则
,即,解得. 12分 22h =1163133
h ??=??1133EBD ABD S h S AE ???=?162EBD S BD OE ?=?=11322
ABD S BD AC ?=?=1113313
C A B
D V -=?=113A B D S ?=
3
2AH =11(12)13333224BCDE V S AH +?=?=??=梯形A BCDE -AH ∴BCDE AH ⊥∴BC DC C =DC AH ∴⊥ABC AH ?ABC DC ⊥AH BC ∴⊥AB BC AC ==AH H BC ADC ADE ⊥∴ADE EF ?ADC EF ∴⊥BG EF ADC BG ∴⊥AC DC C =DC BG ∴⊥ABC BG ?ABC DC ⊥BG AC ∴⊥AC G ABC ?ABC EF ∴ABC BG ?ABC EF ?BG EF ∴BEFG BE FG ∴CD BE 112FG DC ==CD FG ∴AC AD F G ,
BG FG G AC
线面垂直与面面垂直 基础要点 1、若直线αβ所成的角相等,则平面αβ B ) A 、//αβ B 、α不一定平行于β C 、α不平行于β D 、以上结论都不正确 2、在斜三棱柱111ABC A B C -,90BAC ∠=,又1BC AC ⊥,过1C 作1C H ⊥底面ABC ,垂足为H ,则H 一定在( B ) A 、直线AC 上 B 、直线AB 上 C 、直线BC 上 D 、△ABC 的内部 3、如图示,平面α⊥平面β,,,A B AB αβ∈∈与两平面,αβ所成的角分别为4π和6 π ,过A 、B 分别作两平面交线的垂线,垂足为,A B '',则:AB A B ''=( A ) A 、2:1 B 、3:1 C 、3:2 D 、4:3 4、如图示,直三棱柱11ABB DCC -中,190,4ABB AB ∠==, 12,1BC CC ==DC 上有一动点P ,则△1APC 周长的最小值是 5.已知长方体1111D C B A ABCD -中,21==AB A A , 若棱AB 上存在点P ,使得PC P D ⊥1,则棱AD 长 的取值范围是 。 题型一:直线、平面垂直的应用 1.(2014,江苏卷)如图,在三棱锥P-ABC 中,D ,E ,F 分别为 PC ,AC ,AB 的中点. 已知,685PA AC PA BC DF ⊥===,,. 求证:(1) PA DEF 平面;(2) BDE ABC ⊥平面平面 . 证明: (1) 因为D ,E 分别为棱PC ,AC 的中点, 所以DE ∥PA. 又因为PA ? 平面DEF ,DE ?平面DEF , 所以直线PA ∥平面DEF. (2) 因为D ,E ,F 分别为棱PC ,AC ,AB 的中点,PA =6,BC =8,所以DE ∥PA ,DE = 12PA =3,EF =1 2 BC =4. 又因 DF =5,故DF 2=DE 2+EF 2, 所以∠DEF =90°,即DE 丄EF. 又PA ⊥AC ,DE ∥PA ,所以DE ⊥AC. 因为AC∩EF =E ,AC ?平面ABC ,EF ?平面ABC ,所以DE ⊥平面ABC. 线面垂直 线线垂直 面面垂直 B` A` B A α β A B C D 1 B 1 C B 1 1 D A D B A
平面与平面垂直的性质 一、教学重点 对性质定理的理解 二、教学难点 性质定理的引入和证明 三、教学设计 (一)复习回顾 1、面面垂直的定义; 2、面面垂直的判定。(二)探究新知 1、探究问题:教室的黑板所在的平面与地面是什么关系?能否在黑板上画一 条直线与地面垂直? 2、猜想 在一个平面内垂直于它们交线的直线垂直于另一个平面。 3、推理证明 已知:α⊥β,α∩β=AB,CDα,CD⊥AB. 求证:CD⊥β. 证明: 此命题就是面面垂直的性质定理。 定理剖析:(1)面面垂直得到线面垂直; (2)为判定和作出线面垂直提供依据。
(三)概念巩固 练习:判断下列命题的真假 1、若α⊥β,那么α内的所有直线都垂直于β。 2、两平面互相垂直,分别在这两平面内的两直线互相垂直。 3、两平面互相垂直,分别在两平面且互相垂直的两直线一定分别与另一个平面垂直。 4、两平面互相垂直,过一平面内的任一点在该平面内作交线的垂线,则此直线必垂直于另一个平面。 (四)巩固深化、发展思维 思考:设平面α⊥平面β,点C在平面α内,过点C作平面β的垂线CD,直线CD与平面α具有什么位置关系? 猜想:直线CD必在平面α内。 推理证明 (引导)要证直线在平面内,直接证法是依据公理1,需要在直线上找到两点在平面内.已知只有一点C∈α,再找合题意的点很困难.应该采用什么对策? 证明: 注:(1)此题运用了“同一法”来证明; (2)这是面面垂直的另一个性质,它的作用是判定直线在平面内. 3、用语言叙述就是:;
(五)应用巩固 上面我们研究了面面垂直的两个性质定理。定理1是判定线面垂直的有效方法,性质2是判定直线在平面内的一种方法。 已知:α⊥γ,β⊥γ,α∩β=a。 求证:a⊥γ. (引导)本题条件是面面垂直,结论是线面垂直.选择适当的判定线面垂直的方法,给出证明. 证明: 此题还可采用间接的证明方法,请同学们课下尝试着用同一法来证明此题。(六)课堂总结 1.这节课我们学习了哪些内容?我们是如何得到这些结论的? 2.空间垂直关系有哪些?如何实现垂直关系的相互转化?指出下图中空间垂直关系转化的依据? 线线垂直线面垂直面面垂直 (七)课堂作业 1、课本73页练习 2、课本74页习题B组第3题 四.目标检测: (一)基础达标 1.P A垂直于以AB为直径的圆所在平面,C为圆上异于A、B的任一点,则下列关系不正确的是(). A. PA⊥BC B. BC⊥平面PAC C. AC⊥PB D. PC⊥BC 2.(1998上海卷)在下列说法中,错误的是(). A. 若平面α内的一条直线垂直于平面β内的任一直线,则α⊥β B. 若平面α内任一直线平行于平面β,则α∥β C. 若平面α⊥平面β,任取直线l α,则必有l⊥β
直线、平面垂直的判定与性质 【知识梳理】 一、直线与平面垂直的判定与性质 1、 直线与平面垂直 (1)定义:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直,记作l ⊥α,直线l 叫做平面α的垂线,平面α叫做直线l 的垂面。如图,直线与平面垂直时,它们唯一公共点P 叫做垂足。 (2)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。 结论:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,记作.//a b b a αα? ?⊥?⊥? (3)性质定理:垂直于同一个平面的两条直线平行。即,//a b a b αα⊥⊥?. 由定义知:直线垂直于平面内的任意直线。 2、 直线与平面所成的角 平面的一条斜线和它在平面上的射影所成的锐角或者直角叫做这条直线和这个平面所成的角。一条直线垂直于平面,该直线与平面所成的角是直角;一条直线和平面平行,或在平面内,则此直线与平面所成的角是0 0的角。 3、 二面角的平面角 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。如果记棱为l ,那么两个面分别为αβ、的二面角记作l αβ--.在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则两射线所构成的角叫做叫做二面角的平面角。其作用是衡量二面角的大小;范围:0 0180θ≤≤. 二、平面与平面垂直的判定与性质 1、定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直. 2、判定:一个平面过另一个平面的垂线,则这两个平面垂直。简述为“线面垂直,则面面垂直”,记作 l l βαβα⊥? ?⊥??? . 3、性质:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直,记作l m m m l αβαββα⊥??=? ?⊥??? ?⊥? I . 【经典例题】 【例1】(2012浙江文)设l 是直线,a,β是两个不同的平面 ( ) A .若l ∥a,l ∥β,则a ∥β B .若l ∥a,l ⊥β,则a ⊥β C .若a ⊥β,l ⊥a,则l ⊥β D .若a ⊥β, l ∥a,则l ⊥β 【答案】B
§2.3.4平面与平面垂直的性质 教学目标: 1.进一步巩固和掌握面面垂直的定义、判定 2.使学生理解和掌握面面垂直的性质定理 3.让学生在观察物体模型的基础上进行操作确认,获得对性质定理的认识 教学重、难点: 重点:理解和掌握面面垂直的性质定理和推导 难点:运用性质定理解决实际问题 教学过程: 师:好,在上课之前我们来回顾一下前面的面面垂直的定义和判定。我们了解到两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。 这是面面垂直的定义,假设我们把定义中的条件和结论交换,也就是说两个平面垂直,那么它们所成的二面角是直二面角这个命题是成立的。 而判定定理是:一个平面过另一平面的垂线,则这两个平面垂直。这是通过线面垂直得到的面面垂直,那么能否通过面面垂直得到线面垂直呢?而这一问题就是这就可要研究的: (§2.3.4平面与平面垂直的性质)
那我们来探究这样一个问题:黑板所在的平面与地面所在的平面垂直,能否在黑板所在的平面内作一条直线与地面垂直? 现在把这个问题数学符号化: 已知:α⊥βα∩β=CD 求证:β内一直线与α垂直 在右边把这两个平面的形象图作出来: 分析:要证明一条直线与一个平面垂直,这就需要证明这条直线与平面内的两条相交直线垂直,这是前面学的直线与平面垂直的判定定理,那么就需要在这个平面内找两条相交直线都与这条直线垂直,那不妨在β内作BE⊥CD于点B,在α内过点B作AB⊥CD
证明: 在β内作BE⊥CD于点B,在α内过点B作AB⊥CD BE⊥CD 二面角∠ABE为直二面角α⊥βα∩β=CD AB⊥BE CD⊥BE BE⊥α AB∩CD=B 这样上面的问题就得以解决证明 像这样的,两个平面垂直,其中一个平面内一条直线垂直于两个平面的交线,那么这条直线垂直与另一个平面,我们把满足这样的性质叫做面面垂直的性质定理 定理:两个平面垂直,则一个平面内垂直于交线的直线与另一平面垂直。 我们的性质定理是通过面面垂直得到线面垂直,前面所学的面面垂直判定是由线面垂直得到面面垂直,这些转化关系在以后解题中有很大的作用,所以啊在解题的时候同学们需要抓住解题的关键之处。 接下来看到书上第二个思考题 思考一:设α⊥β,点P在平面α内,过点P 作β的垂线a,那么直线a与α有什么位置关系?
立体几何证明------垂直 一.复习引入 1.空间两条直线的位置关系有:_________,_________,_________三种。 2.(公理4)平行于同一条直线的两条直线互相_________. 3.直线与平面的位置关系有_____________,_____________,_____________三种。 4.直线与平面平行判定定理:如果_________的一条直线和这个平面的一条直线平行, 那么这条直线和这个平面平行 5.直线与平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这 个平面相交,那么_________________________. 6.两个平面的位置关系:_________,_________. 7.判定定理1:如果一个平面有_____________直线都平行于另一个平面,那么这两 个平面平行. 8.线面垂直性质定理:垂直于同一条直线的两个平面________. 9.如果两个平行平面同时和第三个平面相交,那么它们的________平行. 10.如果两个平面平行,那么其中一个平面的所有直线都_____于另一个平面. 二.知识点梳理 要点诠释:定义中“平面的任意一条直线”就是指“平面的所有直线”,这与“无数条直线”不同(线 线垂直线面垂直) Ⅰ.二面角:从一条直线出发的两个半平面所组成的图形叫二面角(dihedral angle ). 这条直线叫做二 面角的棱,这两个半平面叫做二面角的面. 记作二面角AB αβ--. (简记P AB Q --)
二面角的平面角的三个特征: ⅰ. 点在棱上 ⅱ. 线在面 ⅲ. 与棱垂直 Ⅱ.二面角的平面角:在二面角αβ-l -的棱l 上任取一点O ,以点O 为垂足,在半平面,αβ分别作垂直于棱l 的射线OA 和OB ,则射线OA 和OB 构成的AOB ∠叫做二面角的平面角. 作用:衡量二面角的大小;围:000180θ<<. 知识点四、平面和平面垂直的定义和判定 (垂直问题中要注意题目中的文字表述,特别是“任何”“ 随意”“无数”等字眼) 三.常用证明垂直的方法 立体几何中证明线面垂直或面面垂直都可转化为线线垂直,而证明线线垂直一般有以下的一些方法: (1) 通过“平移”。 (2) 利用等腰三角形底边上的中线的性质。 (3) 利用勾股定理。 (4) 利用直径所对的圆周角是直角 (1) 通过“平移”,根据若则a //b,且b⊥平面α,a⊥平面α 1.在四棱锥P-ABCD 中,△PBC 为正三角形,AB ⊥平面PBC ,AB ∥CD ,AB=2 1 DC ,中点为PD E . 求证:AE ⊥平面PDC. 2.如图,四棱锥P -ABCD 的底面是正方形,PA ⊥底面ABCD , ∠PDA=45°,点E 为棱AB 的中点.求证:平面PCE ⊥平面PCD ; (第2题
一、判定两线平行的方法 1、平行于同一直线的两条直线互相平行 2、垂直于同一平面的两条直线互相平行 3、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线 就和交线平行 4、如果两个平行平面同时和第三个平面相交,那么它们的交线平行 5、在同一平面内的两条直线,可依据平面几何的定理证明 二、判定线面平行的方法 1、据定义:如果一条直线和一个平面没有公共点 2、如果平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平 行 3、两面平行,则其中一个平面内的直线必平行于另一个平面 4、平面外的两条平行直线中的一条平行于平面,则另一条也平行于该平面 5、平面外的一条直线和两个平行平面中的一个平面平行,则也平行于另一个平面 三、判定面面平行的方法 1、定义:没有公共点 2、如果一个平面内有两条相交直线都平行于另一个平面,则两面平行 3 垂直于同一直线的两个平面平行 4、平行于同一平面的两个平面平行 四、面面平行的性质 1、两平行平面没有公共点 2、两平面平行,则一个平面上的任一直线平行于另一平面 3、两平行平面被第三个平面所截,则两交线平行 4、垂直于两平行平面中一个平面的直线,必垂直于另一个平面 五、判定线面垂直的方法 1、定义:如果一条直线和平面内的任何一条直线都垂直,则线面垂直 2、如果一条直线和一个平面内的两条相交线垂直,则线面垂直 3、如果两条平行直线中的一条垂直于一个平面,则另一条也垂直于该平面 4、一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面 5、如果两个平面垂直,那么在一个平面内垂直它们交线的直线垂直于另一个平面 6、如果两个相交平面都垂直于另一个平面,那么它们的交线垂直于另一个平面 六、判定两线垂直的方法 1、定义:成90 角 2、直线和平面垂直,则该线与平面内任一直线垂直 3、在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线 垂直 4、在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影 垂直 5 、一条直线如果和两条平行直线中的一条垂直,它也和另一条垂直 七、判定面面垂直的方法 1、定义:两面成直二面角, 则两面垂直 2、一个平面经过另一个平面的一条垂线,则这个平面垂直于另一平面 八、面面垂直的性质 1、二面角的平面角为90
怎么证明面面垂直证明一个面上的一条线垂直另一个面;首先可以转化成 一个平面的垂线在另一个平面内,即一条直线垂直于另一个平面 然后转化成 一条直线垂直于另一个平面内的两条相交直线 也可以运用两个面的法向量互相垂直。 这是解析几何的方法。 证:连接AC,BD.PD垂直面ABCD=>PD垂直AC.ABCD为正方形=>AC垂直BD.而BD是PB 在面ABCD内的射影=>PB垂直AC.PD垂直AC=>AC垂直面PBD.AC属于面ACE=>面PBD 垂直面ACE 2 1利用直角三角形中两锐角互余证明 由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°,即直角三角形的两个锐角互余。 2勾股定理逆定理 3圆周角定理的推论:直径所对的圆周角是直角,一个三角形的一边中线等于这边的一半,则这个三角形是直角三角形。 二、高中部分 线线垂直分为共面与不共面。不共面时,两直线经过平移后相交成直角,则称两条直线互相垂直。 1向量法两条直线的方向向量数量积为0 2斜率两条直线斜率积为-1 3线面垂直,则这条直线垂直于该平面内的所有直线 一条直线垂直于三角形的两边,那么它也垂直于另外一边 4三垂线定理在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。 5三垂线定理逆定理如果平面内一条直线和平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。 3高中立体几何的证明主要是平行关系与垂直关系的证明。方法如下(难以建立坐标系时再考虑): Ⅰ.平行关系: 线线平行:1.在同一平面内无公共点的两条直线平行。2.公理4(平行公理)。3.线面平行的性质。4.面面平行的性质。5.垂直于同一平面的两条直线平行。 线面平行:1.直线与平面无公共点。2.平面外的一条直线与平面内的一条直线平行。3.两平面平行,一个平面内的任一直线与另一平面平行。 面面平行:1.两个平面无公共点。2.一个平面内的两条相交直线分别与另一平面平行。Ⅱ.垂直关系: 线线垂直:1.直线所成角为90°。2.一条直线与一个平面垂直,那么这条直线与平面内的任一直线垂直。 线面垂直:1.一条直线与一个平面内的任一直线垂直。2.一条直线与一个平面内的两条相交直线都垂直。3.面面垂直的性质。4.两条平行直线中的一条垂直与一个平面,那么另一直线也与此平面垂直。5.一条直线垂直与两个平行平面中的一个,那么这条直线也与另一平面垂直。 面面垂直:1.面面所成二面角为直二面角。2.一个平面过另一平面的垂线,那么这两个平面垂直。
直线、平面垂直的判定与性质 【考纲说明】 1、能够认识和理解空间中线面垂直的有关性质和判定定理。 2、能够运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题。 【知识梳理】 一、直线与平面垂直的判定与性质 1、 直线与平面垂直 (1)定义:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直,记作l ⊥α,直线l 叫做平面α的垂线,平面α叫做直线l 的垂面。如图,直线与平面垂直时,它们唯一公共点P 叫做垂足。 (2)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。 结论:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,记作.//a b b a αα? ?⊥?⊥? (3)性质定理:垂直于同一个平面的两条直线平行。即,//a b a b αα⊥⊥?. 由定义知:直线垂直于平面内的任意直线。 2、 直线与平面所成的角 平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角。一条直线垂直于平面,该直线与平面所成的角是直角;一条直线和平面平行,或在平面内,则此直线与平面所成的角是0 0的角。 3、 二面角的平面角 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。如果记棱为l ,那么两个面分别为αβ、的二面角记作l αβ--.在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则两射线所构成的角叫做叫做二面角的平面角。其作用是衡量二面角的大小;范围:0 0180θ<<. 二、平面与平面垂直的判定与性质 1、定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直. 2、判定:一个平面过另一个平面的垂线,则这两个平面垂直。简述为“线面垂直,则面面垂直”,记作 l l βαβα⊥? ?⊥??? .
如何证明线面垂直∵PA⊥平面α,直线L∈平面α ∴PA⊥L========================① ∵PB⊥平面β,直线L∈平面β ∴PB⊥L========================② 综合①②得: 直线L⊥平面PAB(垂直于平面两条相交直线的直线垂直于这个平面) ∴L⊥AB(垂直于平面的直线垂直于平面内的任一直线) 线面垂直的判定定理证明,我一直觉得证明过程太过复杂。前年曾经这样证明,今天写在这里。m和n为平面中两条相交直线,通过平移或者说原本就在,使得l经过m、n的交点O,我们只需证明l垂直与平面中的任意一条直线g 即可!在m、n上分别以O点为中点截取AC、BD,则得到平行四边形ABCD。此时不难由三角形全等的知识得到l⊥g。 答案补充 证明:已知直线L1 L22相交于O点且都与直线L垂直,L3是L1 L2所在平面内任意1条不与L1 L2重合或平行的直线(重合或平行直接可得它与L1平行) 在L3上取E、F令OE=OF,分别过E、F作ED、FB交L2于D、B (令OD=OB)则⊿OED ≌⊿ OFB (SAS) 延长DE、BF分别交 L1于A、C 则⊿OEA≌⊿OFC(ASA)(注意角AEO与角CFO的补角相等所以它们相等)。所以OA=OC,所以⊿OAD≌⊿OBC(SAS)所以AD=CB 因为L3垂直于L1 L2所以MA=MC,MD=MB 所以⊿MAD≌⊿MCD(SSS)所以角MAE= 角MCF 所以⊿MAE≌⊿MCF(SAS) 所以ME=MF,所以⊿MOE≌⊿MOF(SSS),所以角MOE=角MOF 又因为角MOE与角MOF互补,所以角MOE=角MOF=90度,即L⊥L3 1利用直角三角形中两锐角互余证明 由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°,即直角三角形的两个锐角互余。 2勾股定理逆定理 3圆周角定理的推论:直径所对的圆周角是直角,一个三角形的一边中线等于这边的一半,则这个三角形是直角三角形。 二、高中部分 线线垂直分为共面与不共面。不共面时,两直线经过平移后相交成直角,则称两条直线互相垂直。 1向量法两条直线的方向向量数量积为0 2斜率两条直线斜率积为-1 3线面垂直,则这条直线垂直于该平面内的所有直线 一条直线垂直于三角形的两边,那么它也垂直于另外一边 4三垂线定理在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。 5三垂线定理逆定理如果平面内一条直线和平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。 2高中立体几何的证明主要是平行关系与垂直关系的证明。方法如下(难以建立坐标系时再考虑): Ⅰ.平行关系: 线线平行:1.在同一平面内无公共点的两条直线平行。2.公理4(平行公理)。3.线面平行的性质。4.面面平行的性质。5.垂直于同一平面的两条直线平行。 线面平行:1.直线与平面无公共点。2.平面外的一条直线与平面内的一条直线平行。3.两平面平行,一个平面内的任一直线与另一平面平行。 面面平行:1.两个平面无公共点。2.一个平面内的两条相交直线分别与另一平面平行。
面面垂直的判定 1、如图,棱柱ABC A1B1C1的侧面 BCC1 B1是菱形,且 B1C A1B 证明:平面 AB1C平面A1BC1 2、如图 ,AB 是⊙O的直径 ,PA 垂直于⊙ O所在的平面 ,C 是圆周上不同于 A,B 的任意一点 , 求证 : 平面 PAC⊥平面 PBC. 3、如图所示,四棱锥P-ABCD的底面 ABCD是菱形,∠ BCD=60°,E 是 CD的中点, PA ⊥底面 ABCD,求证:平面 PBE⊥平面 PAB;
4、如图,在四面体ABCD中, CB=CD, AD⊥BD,点 E、 F 分别是 AB、BD的中点.求证:(1) 直线 EF∥平面 ACD; (2) 平面 EFC⊥平面 BCD. 5、如图 , 在四棱锥 S-ABCD中, 底面 ABCD是正方形 ,SA⊥底面 ABCD,SA=AB,点 M是 SD 的中点 ,AN⊥SC,且交 SC于点 N. (I) 求证 :SB∥平面 ACM; (II)求证:平面SAC⊥平面AMN.
面面垂直的性质 1、S 是△ ABC所在平面外一点, SA⊥平面 ABC,平面 SAB⊥平面 SBC,求证 AB⊥BC. 2、在四棱锥中,底面ABCD是正方形,侧面VAD是正三角形, 平面 VAD⊥底面 ABCD证明 :AB⊥平面 VAD
3、如图,平行四边形 ABCD 中,DAB 60,AB 2, AD 4 将CBD沿BD折起到 EBD 的位置,使平面 EDB 平面 ABD 。求证: AB DE 4、如图,在四棱锥P ABCD 中,平面 PAD⊥平面 ABCD,AB=AD, ∠BAD=60°, E、F 分别是 AP、AD的中点 求证:(1)直线 EF‖平面 PCD;(2)平面 BEF⊥平面 PAD
面面垂直的证明及应用 一、单选题(共9道,每道11分) 1.如图,平面α⊥平面β,,AB与两平面α,β所成的角分别为45°和30°,过A,B分别作两平面交线的垂线,垂足为,则( ) A.2:1 B.3:1 C.3:2 D.4:3 2.如图,在四面体P-ABC中,PA=PB=13,平面PAB⊥平面ABC,∠ACB=90°,AC=8, BC=6,则PC的长为( ) A.13 B.12 C.11 D.10 3.如图,边长为6的正方形ABCD和正方形ADEF所在的平面互相垂直,O,M分别是BE,AF的中点,则线段OM的长度为( )
A. B. C. D. 4.如图,在棱长均相等的正三棱柱中,D为的中点,F在上,且 ,则下列结论:①;②;③.其中正确的有( ) A.0个 B.1个 C.2个 D.3个 5.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC 6.如图,在三棱锥S-ABC中,∠SBA=∠SCA=90°,且△ABC是斜边AB=a的等腰直角三角形,给出下列结论:①异面直线SB与AC所成的角为90°;②直线SB⊥平面ABC;③平面SBC⊥平面SAC; ④点C到平面SAB的距离是.其中正确的有( ) A.1个 B.2个 C.3个 D.4个 7.如图,在三棱锥P-ABC中,∠ABC=90°,PA=PB=PC,则下列说法正确的是( )
第六节 面面关系 (一)平行 (二)垂直 1.如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=1 2AA 1,D 是棱 AA 1的中点 (I)证明:平面BDC 1⊥平面BDC (Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比. 2.【2012高考江西文19】(本小题满分12分) 如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,BC=42,DE=4.现将△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合与点G ,得到多面体CDEFG . (1)求证:平面DEG ⊥平面CFG ; (2)求多面体CDEFG 的体积。 3.如图,已知空间四边形中,,BC AC AD BD ==,E 是AB 的中点。 求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。 4.如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点. (1)求证:1//A C 平面BDE ; B 1 C B A D C 1 A 1 A E D B C
A AC⊥平面BDE. (2)求证:平面 1 5.已知四棱锥P—ABCD,底面ABCD是菱形,∠PD DAB, 60平面ABCD,PD=AD, = ⊥ ? 点E为AB中点,点F为PD中点. (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值
第六节 面面关系答案 (一)平行 (二)垂直 1.【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计 算,考查空间想象能力、逻辑推理能力,是简单题. 【解析】(Ⅰ)由题设知BC ⊥1CC ,BC ⊥AC , 1CC AC C ?=,∴BC ⊥面11ACC A , 又∵1DC ?面11ACC A ,∴1DC BC ⊥, 由题设知01145A DC ADC ∠=∠=,∴1CDC ∠=0 90,即1DC DC ⊥, 又∵DC BC C ?=, ∴1DC ⊥面BDC , ∵1DC ?面1BDC , ∴面BDC ⊥面1BDC ; (Ⅱ)设棱锥1B DACC -的体积为1V ,AC =1,由题意得,1V =1121132 +???=1 2, 由三棱柱111ABC A B C -的体积V =1, ∴11():V V V -=1:1, ∴平面1BDC 分此棱柱为两部分体积之比为1:1. 2.【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG GF ⊥ 又因为CF EGF ⊥底面,可得CF EG ⊥,即EG CFG ⊥面所以平面DEG ⊥平面CFG . (2)过G 作GO 垂直于EF ,GO 即为四棱锥G-EFCD 的高,所以所求体积为1112 5520 3 35DECF S GO ?=???=正方形 3.证明:(1) BC AC CE AB AE BE =? ?⊥?=? 同理, AD BD DE AB AE BE =? ?⊥?=? 又∵CE DE E ?= ∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE
立体几何垂直证明方法技巧授课教师:吴福炬
类型一:线线垂直证明(共面垂直、异面垂直) (1) 共面垂直:掌握几种模型 ①等腰(等边)三角形中的中线 ②菱形(正方形)的对角线互相垂直 ③勾股定理中的三角形 ④ 直角梯形 ⑤利用相似或全等证明直角。 例:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心, E 为1CC 中点,求证: (1) 1A O OE ⊥ (2) 1A O BDE ⊥平面
(2) 异面垂直(利用线面垂直来证明) 例1 在正四面体ABCD 中, 求证:AC BD ⊥ 变式1 如图,在四棱锥ABCD P -中,底面ABCD 是矩形, 已知 60,22,2,2,3=∠====PAB PD PA AD AB . 证明:AD PB ⊥;
变式2 如图,在边长为2的正方形ABCD中,点E是AB的中 点,点F是BC的中点,将△AED,△DCF分别沿, DE DF折起, 使,A C两点重合于'A. 求证:'A D EF ⊥; 变式3如图,在三棱锥P ABC -中,⊿PAB是等边三角形, ∠P AC=∠PBC=90 o证明:AB⊥PC 类型二:直线与平面垂直证明 B E ' A D F G
方法○1利用线面垂直的判断定理 例:在正方体1111ABCD A B C D -中,,求证:1 1AC BDC ⊥平面 变式1:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90?.E 为BB 1 的中点,D 点在AB 上且DE = 3 . 求证:CD ⊥平面A 1ABB 1; 变式2:如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的
理科数学复习专题 立体几何 线面垂直与面面垂直专题复习 【知识点】 一.线面垂直 (1)直线与平面垂直的定义: 如果直线l 和平面α的__________一条直线都垂直,我们就说直线l 与平面α垂直,记作__________. 重要性质:__________________________________________________________ (2)直线与平面垂直的判定方法: ①判定定理:一条直线与一个平面的两条__________都垂直,那么这条直线就垂直于这个平面.用符号表示为: ②常用结论:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.用符号可表示为: (3)直线与平面垂直的性质: ①由直线和平面垂直的定义知:直线与平面垂直,则直线垂直于平面的_______直线. ②性质定理:垂直于同一平面的两条直线平行.用符号可表示为: 二、面面垂直 (1)平面与平面垂直的定义: 两平面相交,如果它们所成的二面角是__________,就说这两个平面互相垂直. (2)平面与平面垂直的判定定理: 如果一个平面经过另一个平面的一条__________,那么这两个平面互相垂直.简述为“线面垂直,则面面垂直”, 用符号可表示为: (3)平面与平面垂直的性质: 如果两个平面互相垂直,那么在一个平面垂直于它们交线的直线垂直于另一个平面.用符号可表示为: 【题型总结】 题型一 小题:判断正误 1.“直线l 垂直于平面α的无数条直线”是“l ⊥α”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件 2.已知如图,六棱锥P -ABCDEF 的底面是正六边形,PA ⊥平面ABC .则下列结论不正确的是( ). A.CD ∥平面PAF B.DF ⊥平面PAF C.CF ∥平面PAB D .CF ⊥平面PAD 2. 设m ,n, l 是三条不同的直线,,,αβγ是三个不同的平面,判断命题正误: α αααααββααβαβα//n ,,m //,,n ,//,,//,//,,则⑤则④则③则②则①n m n m n m n m m m m m m ⊥⊥⊥⊥⊥⊥⊥⊥⊥⊥ γ αβγβαγαγββααα⊥⊥⊥⊥⊥⊥⊥⊥⊥⊥则,⑩则⑨则,⑧则⑦则⑥,//m ,//,m //,//m ,,m n ,//,n m l l n n l l n n m
八、三个公理 公理1、判断直线在平面内的依据或者说判定公理。 如果一条直线上有两个点在一个平面内,那么这条直线上的所有点都在这个平面内。 该性质是判定直线在平面内的依据,用集合符号表示为: lα。依据直线在平面内,可以判断点在平面内,即A∈l,lαA∈α. 公理2、判断点在直线上的依据,要判断直线经过点只要证明点在以该直线为供公交线的两个平面内即可。 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。 用集合符号表示为:A∈α,A∈βα∩β=α且A∈α。 由此易知,如果两个平面有两个公共点,那么这两个平面相交于由这两点确定的一条直线,即 α∩β=AB。 依据两平面相交的意义,可以判断点在直线上,即A∈α,A∈β,α∩β=αA∈α。 公理3以及三个推论、确定为一个平面的依据。(1)选不共线的三点(2)选一条直线与直线外一点(3)选两条相交直线(4)选两条平行直线 1.经过不在同一直线上的三点,有且只有一个平面。 2.经过一条直线和这条直线外的一点,有且只有一个平面。 3.经过两条相交直线,有且只有一个平面。 4.经过两条平行直线,有且只有一个平面。 所以在判断或证明时要有针对性地找到依据进行处理。 证明线共点问题基本步骤是:1、两条相交点为A,2、利用A在以另外直线为交线的两个平面上,3、从而确定A在另外直线上。主要依据公理二。 证明线共面问题基本步骤是:1、两条直线或三个不共线点确定一个平面,2、利用公理一说明其他直线在这平面上,3、从而确定直线确定一个平面上。主要依据公理一,三及推论。 对于符号语言判断题,尽可能作出图形或演示出位置进行判断推理。 九、16个定理的记忆 1、平行传递性同类平行具有传递性2个定理 ⑴线 ⑵面 2、平行与垂直的传递性同类平行与异类垂直具有传递性4个定理
线面垂直与面面垂直 基础要点 1、若直线a 与平面,αβ所成的角相等,则平面α与β的位置关系是( B ) A 、//αβ B 、α不一定平行于β C 、α不平行于β D 、以上结论都不正确 2、在斜三棱柱111ABC A B C -,90BAC ∠=,又1BC AC ⊥,过1C 作1C H ⊥底面ABC ,垂足为H ,则H 一定在( B ) A 、直线AC 上 B 、直线AB 上 C 、直线BC 上 D 、△ABC 的内部 3、如图示,平面α⊥平面β,,,A B AB αβ∈∈与两平面,αβ所成的角分别为4π和6 π,过A 、B 分别作两平面交线的垂线,垂足为,A B '',则:AB A B ''=( A ) A 、2:1 B 、3:1 C 、3:2 D 、4:3 4、如图示,直三棱柱11ABB DCC -中,190,4ABB AB ∠==, 12,1BC CC ==DC 上有一动点P ,则△1APC 周长的最小值是 5.已知长方体1111D C B A ABCD -中,21==AB A A , 若棱AB 上存在点P ,使得PC P D ⊥1,则棱AD 长 的取值范围是 。 题型一:直线、平面垂直的应用 1.(2014,江苏卷)如图,在三棱锥P-ABC 中,D ,E ,F 分别为棱PC ,AC ,AB 的中点. 已知,685PA AC PA BC DF ⊥===,,. 求证:(1) PA DEF 平面错误!未找到引用源。;(2) BDE ABC ⊥平面平面 错误!未找到引用源。. 线面垂直 线线垂直 面面垂直 B` A` B A α β A B C D 1 B 1 C B 1 C 1 D 1 A 1 D C B A
垂直证明题常见模型及方法 证明空间线面垂直需注意以下几点: ①由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。 ②立体几何论证题的解答中,利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。 ③明确何时应用判定定理,何时应用性质定理,用定理时要先申明条件再由定理得出相应结论。 垂直转化:线线垂直 线面垂直 面面垂直; 基础篇 类型一:线线垂直证明(共面垂直、异面垂直) (1) 共面垂直:实际上是平面内的两条直线的垂直 (只需要同学们掌握以下几种模型) ○1 等腰(等边)三角形中的中线 ○ 2 菱形(正方形)的对角线互相垂直 ○3勾股定理中的三角形 ○ 4 1:1:2 的直角梯形中 ○ 5 利用相似或全等证明直角。 例:在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1AO OE ⊥ (2) 异面垂直 (利用线面垂直来证明,高考中的意图) 例1 在正四面体ABCD 中,求证AC BD ⊥ 变式 1 如图,在四棱锥ABCD P -中,底面A B C D 是矩形,已知 60,22,2,2,3=∠====PAB PD PA AD AB . 证明:AD PB ⊥; 变式2 如图,在边长为2的正方形ABCD 中,点E 是AB 的中点,点F 是 BC 的中点,将△AED,△DCF 分别沿,DE DF 折起,使,A C 两 点重合于' A . 求证:' A D EF ⊥; B E 'A D F G
变式3如图,在三棱锥P ABC -中,⊿PAB 是等边三角形,∠P AC =∠PBC =90 o证明:AB ⊥PC 类型二:线面垂直证明 方法○1 利用线面垂直的判断定理 例2:在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为1CC ,求证: 1 AO BDE ⊥平面 变式1:在正方体1111ABCD A BC D -中,,求证:11AC BDC ⊥平面 变式2:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90?.E 为BB 1的中点,D 点在AB 上且DE = 3 . 求证:CD ⊥平面A 1ABB 1; AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,AB =,6BC = C E
1.已知如图,P ?平面ABC ,PA=PB=PC ,∠APB=∠APC=60°,∠BPC=90 °求证:平面ABC ⊥平面PBC 【答案】 【解析】要证明面面垂直,只 要在其呈平面内找一条 线,然后证明直线与另一平面垂直即可。显然BC 中点D ,证明AD 垂直平PBC 即可 证明: 取BC 中点D 连结AD 、PD ∵PA=PB ;∠APB=60° ∴ΔPAB 为正三角形 同理ΔPAC 为正三角形 设PA=a 在RT ΔBPC 中,PB=PC=a BC=2a ∴PD=2 2a 在ΔABC 中 AD= 22BD AB - = 2 2a ∵AD 2+PD 2 =2 2 2222??? ? ? ?+???? ??a a =a 2 =AP 2 ∴ΔAPD 为直角三角形 即AD ⊥DP 又∵AD ⊥BC
∴AD ⊥平面PBC ∴平面ABC ⊥平面PBC 2 . 如 图 ( 1 ) 在 直 角 梯形 ABCD 中 , AB ⊥ 12 ⊥1 sin 2 AH BD θ==ED ⊥ABCD ED ⊥BC BCD ?2DB BC ==2DC =BC BD ∴⊥2,DB =D BEF A BEF //AD EF AD ⊥BEF ABF ⊥BEF ABF ?BF A BEF 1C 1C 长方体1AC 中,对角线11//BD B D . ……………2分 又Q E 、F 为棱AD 、AB 的中点, ∴//EF BD . ∴11//EF B D . ……………4分 又B 1D 1 平面11CB D ,EF ?平面11CB D ,∴EF ∥平面CB 1D 1. ……………7分 (2)Q 在长方体1AC 中,AA 1⊥平面A 1B 1C 1D 1,而B 1D 1 平面A 1B 1C 1D 1,∴AA 1⊥B 1D 1.… 9分 又Q 在正方形A 1B 1C 1D 1中,A 1C 1⊥B 1D 1,∴ B 1D 1⊥平面CAA 1C 1. 又Q B 1D 1 平面CB 1D 1,∴平面CAA 1C 1⊥平面CB 1D 1.……14分 4.如图,四棱锥 ABCD P -中,底面 ABCD 为平行四边形, 22==AD AB ,3=BD ,PD ⊥底面ABCD . (1)证明:平面⊥PBC 平面 PBD ; A B C D E 图2 A B E C 图1 F D A B C D A 1 B 1 1 D 1 E F
1 / 4 空间线线、线面、面面垂直关系练习题 一、填空题 1.给出下列三个命题: ①“直线a 、b 为异面直线”的充分非必要条件是“直线a 、b 不相交”; ②“直线a 垂直于直线b ”的充分非必要条件是“直线a 垂直直线b 在平面β内的射影”; ③“直线a 垂直平面β” 的必要非充分条件是“直线a 垂直于平面β内的无数条直线” 其中所有真命题的序号是 ③ 2.如图,正方形ABCD ,P 是正方形平面外的一点,且P A ⊥平面A BCD 则在△P AB 、△PBC 、△PCD 、△P AD 、△P AC 及△PBD 中,为直角三角形有______5___个. 3.在四棱锥P-ABCD 中,P A ⊥底面ABCD ,底面各边都相等,M 是PC 上的一动点,当点M 满足 BM PC ⊥ 时,平面MBD ⊥平面PCD . 4.已知三棱锥ABC S -的底面是正三角形,点A 在侧面SBC 上的射影 H 是SBC ?的垂心,且SA 的长为定值,则下列关于此三棱锥的命题:①点B 在侧面SAC 上的射影是SAC ?的垂心;②三棱锥ABC S -是一个正三棱锥;③三棱锥ABC S -的体积有最大值;④三棱锥ABC S -的体积有最小值.其中正确命题的序号为 ①②③ . 5.如果a,b 是异面直线,P 是不在a,b 上的任意一点,下列四个结论:(1)过P 一定可作直线L 与a , b 都相交;(2)过P 一定可作直线L 与a , b 都垂直;(3)过P 一定可作平面α与a , b 都平行;(4)过P 一定可作直线L 与a , b 都平行,其中正确的结论有___(2)______. 6.给出下列命题:①分别和两条异面直线AB .CD 同时相交的两条直线AC .BD 一定是异面直线②同 时与两条异面直线垂直的两直线不一定平行③斜线b 在面α内的射影为c ,直线a ⊥c ,则a ⊥b ④有三个角为直角的四边形是矩形,其中真命题是 ① . 7.点P 在直径为2的球面上,过P 作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和为最大值是 5 70 2 . 8.正四面体ABCD 的棱长为1,棱AB //平面α,则正四面体上 的所有点在平面α内的射影构成图形面积的取值范围是 ]21 ,42[ . 9.直二面角α-l -β的棱l 上有一点A ,在平面α、β内各有一条射线AB ,AC 与l 成450,AB βα??AC ,, 则∠BAC= .(60o 或120o ,两种情形) 10.四棱锥D ABCE -的底面是矩形,DE ⊥面ABCE ,3,1, 2.DE EC BC G ===为DA 的中点,Q 为DC 上一点,且EQ ⊥面GBC ,则 DQ QC = 3 2 . 11.已知边长为23的正ABC ?,点,D E 分别在边,AB AC 上,且//DE BC ,以 DE 为折痕,把ADE ?折起至A DE '?,使点A '在平面BCED 上的射影H 始 终落在BC 边上,记2ADE S A H ?='的面积 ,则S 的取值范围为 . 【答案】3 ( ,)3 +∞【解析】设A 到DE 的距离为x ,则DE 与BC 间距离为3x -,ADE ∴?的面积为233 x ()222 369A H x x x '=--=- 2339232x S x x ??∴=?> ?-?? S ∴的取值范围为3(,)3+∞ . 12.三棱锥ABC P -中,?=∠=∠=∠90CPA BPC APB ,点M 在△ABC 内,且=∠MPA ?=∠60MPB ,则MPC ∠的度数是___?45______. 13.如图,AD 与BC 是四面体ABCD 中互相垂直的棱,2=BC ,若c AD 2=,且a CD AC BD AB 2=+=+,其中a 、c 为常数,则四面体ABCD 的体积的最 大值是 。【答案】 13 2 22--c a c 14.如图,已知平面α⊥平面β,A 、B 是平面α与平面β的交线上的两个定点,,DA CB ββ??,且DA α⊥,CB α⊥,4AD =,8BC =,6AB =,在平面α上有一个动点P ,使得APD BPC ∠=∠,则PAB ?的面积的最大值是 12 . 二、解答题 15. 如图,正方形ABCD 所在的平面与三角形CDE 所在的平面交于CD ,AE ⊥平面CDE ,且 2AB AE =. (1)求证://AB 平面CDE ; (2)求证:平面ABCD ⊥平面ADE ; 证明:(1)正方形ABCD 中,//AB CD ,又AB ?平面CDE , CD ?平面CDE , 所以//AB 平面CDE . (2)因为AE CDE ⊥平面,且CD CDE ?平面, 所以AE CD ⊥, 又 ABCD CD AD ⊥正方形中,, 且AE AD A =I AE AD ADE ?、平面, 所以CD ADE ⊥平面, 又CD ABCD ?平面, 所以ABCD ADE ⊥平面平面. 16.如图所示,△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,EC =CA =2BD ,M 是EA 的中点. 求证:(1)平面BDM ⊥平面ECA (2)平面DEA ⊥平面ECA 17.如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,AB DC ∥, PAD △是等边三角形,已知28BD AD ==,245AB DC ==. (1)设M 是PC 上的一点,证明:平面MBD ⊥平面PAD ; (2)求四棱锥P ABCD -的体积. (1) 证明:在ABD △中,由于4AD =,8BD =, 45AB =,所以222AD BD AB +=.故AD BD ⊥. 又平面PAD ⊥平面ABCD ,平面PAD I 平面ABCD AD =, BD ?平面ABCD ,所以BD ⊥平面PAD , 又BD ?平面MBD ,故平面MBD ⊥平面PAD . (2) 解:过P 作PO AD ⊥交AD 于O ,由于平面PAD ⊥平面ABCD , 所以PO ⊥平面ABCD .因此PO 为四棱锥P ABCD -的高,又PAD △是边长为4的等边三角形.因此3 4232 PO =?=.在底面四边形ABCD 中,AB DC ∥,2AB DC =,所以四边形ABCD 是梯形,在Rt ADB △中,斜边AB 边 上的高为4885 545 ?= , α β P A B D C A B C D E A B C M P D