构造辅助圆

构造辅助圆，交点立显现

在解一些几何问题时，常会遇到一些用常规方法很难解决的问题。这时，如果构造适当的图形来给以辅助，往往能促使问题转化，使问题中原来隐晦不清的关系和性质在新构造的环境中清晰地展现出来，从而简捷地解决问题，这种解题方法称为构造法。

对于在已知条件的线上找点与已知点构成一定的角的问题，如果能根据题目的题设和结论，构造出符合题意特征的辅助圆，即把题目中的固定角转化为圆的圆周角问题，就能使问题得以顺利解决，这种方法利用数形结合，使代数与几何等知识相互渗透，综合应用，它不但能较好的达到解题的目的，还有利于培养学生分析问题的能力。请看下面的两个例题：例1：（06东营）如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是

（A）3个（B）2个（C）1个（D）不存在

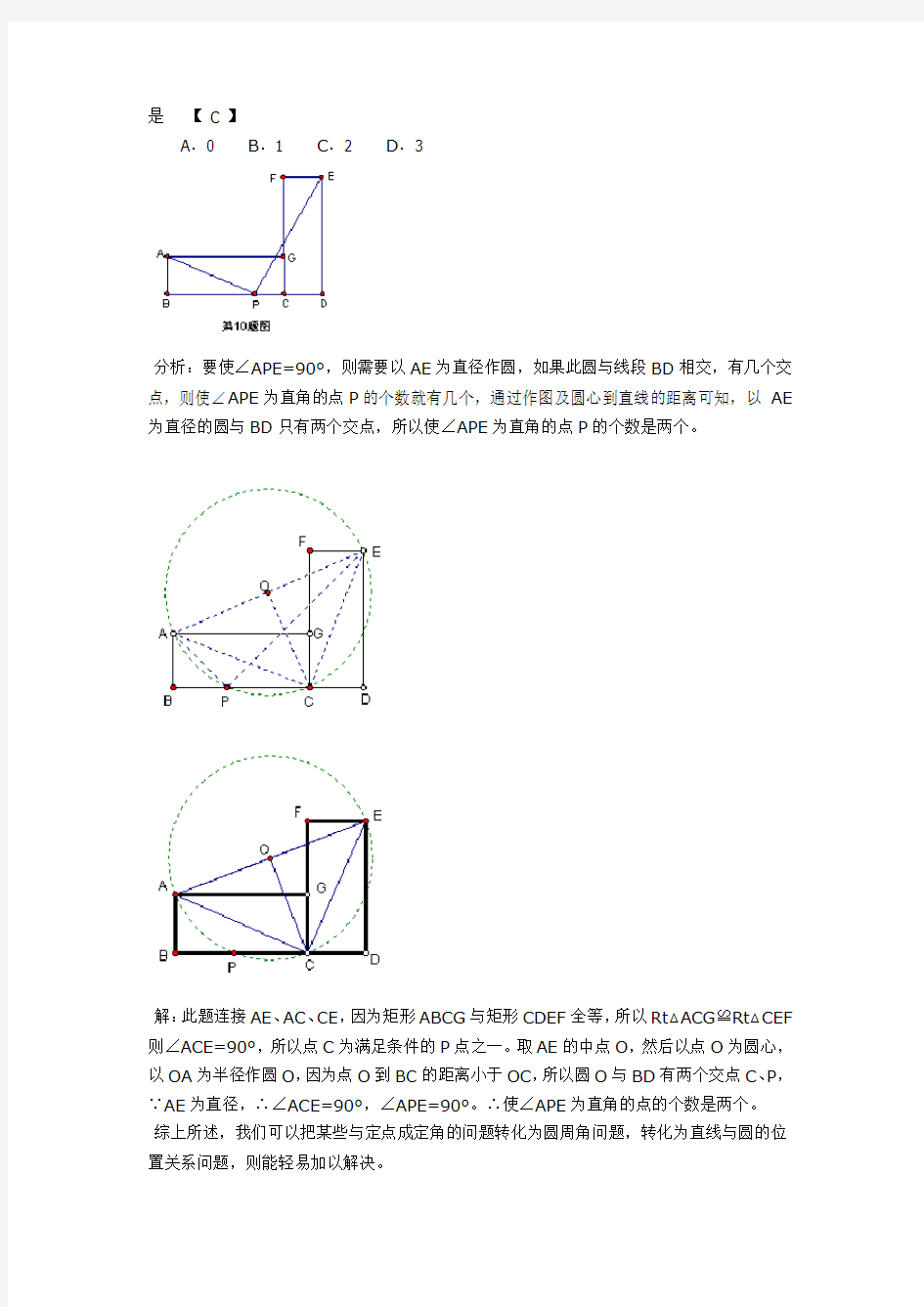
分析：要在直线l上找点P使∠APB=30°，可以构造以AB为边作等边三角形ABO，则∠AOB=60°，然后以O为圆心，AB为半径，作圆O，如图，∵△ABO为等边三角形∴OB∥l，∴点O到l的距离d

解：此题如果以AB为边作等边△ABO,再以点O为圆心，AB为半径作圆交直线l与点P1、P2，∵∠AOB=60°∴∠AP1B=30°，∠AP2B=30°所以满足条件的点P的个数是两个，分别为P1、P2。

例2：（06陕西）如图，矩形ABCG（）与矩形CDEF全等，点B、C、D在同一条直线上，的顶点P在线段BD上移动，使为直角的点P的个数

是【 C 】

A．0 B．1 C．2 D．3

分析：要使∠APE=90°，则需要以AE为直径作圆，如果此圆与线段BD相交，有几个交点，则使∠APE为直角的点P的个数就有几个，通过作图及圆心到直线的距离可知，以AE 为直径的圆与BD只有两个交点，所以使∠APE为直角的点P的个数是两个。

解：此题连接AE、AC、CE，因为矩形ABCG与矩形CDEF全等，所以Rt△ACG≌Rt△CEF 则∠ACE=90°，所以点C为满足条件的P点之一。取AE的中点O，然后以点O为圆心，以OA为半径作圆O，因为点O到BC的距离小于OC，所以圆O与BD有两个交点C、P，∵AE为直径，∴∠ACE=90°，∠APE=90°。∴使∠APE为直角的点的个数是两个。

综上所述，我们可以把某些与定点成定角的问题转化为圆周角问题，转化为直线与圆的位置关系问题，则能轻易加以解决。

浅谈构造辅助圆解决点的问题

浅谈构造辅助圆解决点的问题 对于数学中较全面、有简易解题方法且不易看出知识点的题目，如果可以根据题干中的基本要素，结合到圆的相应理论，合适地画出辅助圆，一般可以变复杂为简单，变困难为基础，发现答题技巧，添加辅助圆的一般过程是：基于“圆的定义”添加辅助圆、通过“圆周角的性质”添加辅助圆、通过圆周角与圆内外角的联系添加辅助圆、基于“弦切角的模型”添加辅助圆、利用“圆幂定理”添加辅助圆、利用“判定四点共圆的理论”添加辅助圆、利用“两圆相切的定义”添加辅助圆、利用“托勒密理论”添加辅助圆。 标签：数学问题添加辅助圆基础题型 从全国高中数学联赛与国际数学奥林匹克中涉及的相关题型来看，可以了解到，数学问题，作为竞赛中最常涉及的内容之一，在数学竞赛中，其地位是数一数二的。对于一些较全面、有简易解题方法且不易看出知识点的题目而言，解题的人哪怕是在灵活运用所学知识与思维逻辑推算方面有着较强的能力，但是难免也会被此绊住脚步。因此，解题者如果可以通过题干基本框架及特征，从而联系到圆的理论应用，合适地添加辅助圆，通常能够变复杂为简单，变困难为基础，从而发现答题的关键出口。本篇文章的中心就是介绍如何利用添加辅助圆来达到解题目的。 在日常的教授课程中，老师们常会根据圆的性质来添加辅助圆，由此便将原有问题变成了辅助圆与直线的公共点的相应问题。 一、根据“在同一个圆内，若两弧相等，则两弧对的圆周角相等”添加辅助圆 题1 如图所示，平行四边形ABCD中，E在AD，延长CE至F点，使得。 （1）证明：； （2）用做图工具在直线AD上取一点P，使∠CPB=∠PDC（作法不需写，保留作图印记） （1）由题目可知AD//BC，所以。 又，所以可以知道，由此可得。 （2）因为P在直线AD上，又AD//BC，所以。若要得，就是要使得，从（1）可以知道条件，则只需，也就是和可以视为弧BC对应的圆周角，因此P 点为的外接圆和AD所相交的点。 解（1）省略。

2017年中考专题复习—辅助圆教学设计

2017年中考专题复习—辅助圆教学设计 学生情况分析：作为专题复习，初三的学生已经学习了圆的基本知识,掌握了圆的一些有关性质,并对辅助圆有了初步的认识.对于直线形中常见的几何问题形成了一些基本的解题策略,但从辅助圆这个新的视角解决问题还显得弱了很多.学生对于一些数学问题容易产生想法,但欠缺的是归纳总结提升,而本节课想要达到的目的,就是引导学生学会归纳总结,将以前学过的一些知识从一个新的视角研究,简化证明过程.初步形成构造曲线形辅助线的意识. 设计意图：对于平面几何问题,学生常常想到的是构造直线形辅助线来转化条件,从而利用三角形、四边形的知识来解决问题.但辅助线的添加就被局限在直线形,而实际上曲线形辅助线在一些特定条件下,更有利于条件的集中,辅助圆是曲线形辅助线的代表,利用圆，就会让图形的条件更丰富，而学生对此又很少了解，故想借此节课，和学生一起探究，来感受辅助圆的独特.本节课想以一种学生探究，老师引领学生作归纳总结的形式呈现，通过学生思想的碰撞，最终达成共识. 教学目标：1.进一步巩固圆的定义和性质，能够正确利用圆找到符合条件的点所在的位置； 2.通过对例题条件和结论的分析，体会利用圆解决点的轨迹问题，进而掌握利用作圆解决分类讨论问题的方法； 3.逐步建立从圆的观点看问题的意识，能够多角度认识事物，全面还原事物的本质. 教学重点：利用辅助圆解决有关问题 教学难点：建立用圆的观点看问题的意识，能够判断出构造圆的条件 教学过程： 画辅助圆即“四点共圆”这类问题一般有两形式：一是要证明某四点共圆（；二是通过某四点共圆来得到一些重要的结果，进而解决问题，下面是与画辅助圆有关的一些基本知识。 1、若干个点与某定点的距离相等，则这些点在同一圆周上（证明多个点到同一个定点的距离相等即可） 2、在若干个点中有两点，其他点对这两点所成线段的视角均为直角，则这些点共圆。（共斜边的两个直角三角形顶点共圆） 3、若四点连成的四边形对角互补或有一外角等于它的内对角，则这四点共圆 4、若点C，D在线段AB的同侧，且∠ACB=∠ADB，则A，B，C，D四点共圆探究1 1、如图所示，在四边形ABCD中，AB=AC=AD，∠BAC=20° ∠CAD=80°，则∠BDC=______度，∠DBC=______度

中考复习讲义三种构造辅助圆解题的模型

中考热点:三种构造辅助圆解题的模型 一、问题导读 “圆”是一个完美的图形，在初中数学中具有丰富内容，其中大部分是与角度相关性质，如在圆周角中能轻易找到，等角和直角并与圆心角联系也比较紧密，通过在图形中构造辅助圆往往能获得意想不到的效果，如果题目中出现了以下条件：三点及三点以上到同一点距离相等，作辅助圆；同一侧有相等的角，或者需要构造出相等的角时，作辅助圆；若一个四边形的一组对角互补，则它的四个顶点共圆．在这些情况下，借助圆去解决一些问题都是非常好的一个选择，下面举例说明这三种构造辅助圆解题的模型应用。 二、典例精析 类型1 根据共端点等线段模型，根据圆的定义构造圆 1.如图，已知OA＝OB＝OC，且∠AOB＝k∠BOC，则∠ACB是∠BAC的（） A．k/2倍 B．k倍 C．2k D．1/k 【分析】由OA＝OB＝OC，得到A，B，C在以O为圆心的同一个圆上，则∠AOB＝2∠ACB，∠BOC＝2∠BAC，而∠AOB＝k∠BOC，即可得到∠ACB＝k∠BAC． 【解答】∵OA＝OB＝OC，∴A，B，C在以O为圆心的同一个圆上，如图，

∴∠AOB＝2∠ACB，∠BOC＝2∠BAC， 而∠AOB＝k∠BOC，即2∠ACB＝k2∠BAC，∴∠ACB＝k∠BAC．故选：B． 2.如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是（） A．1.5 B．1.2 C．2.4 D．以上都不对 【分析】先依据勾股定理求得AB的长，然后依据翻折的性质可知PF＝FC，故此点P在以F为圆心，以2为半径的圆上，依据垂线段最短可知当FP⊥AB时，点P到AB的距离最短，然后依据题意画出图形，最后，利用相似三角形的性质求解即可． 【解答】如图所示：当PE∥AB． 在Rt△ABC中，∵∠C＝90°，AC＝6，BC＝8，∴由勾股定理可求得AB＝10， 由翻折的性质可知：PF＝FC＝2，∠FPE＝∠C＝90°． ∵PE∥AB，∴∠PDB＝90°．由垂线段最短可知此时FD有最小值． 又∵FP为定值，∴PD有最小值． 又∵∠A＝∠A，∠ACB＝∠ADF，∴△AFD∽△ABC． ∴AF/AB=DF/BC，即4/10=DF/8，解得：DF＝3.2． ∴PD＝DF﹣FP＝3.2﹣2＝1.2．故选：B．

中考复习讲义：三种构造辅助圆解题的模型

中考热点:三种构造辅助圆解题的模型一、问题导读 其中大“圆”是一个完美的图形，在初中数学中具有丰富内容，等角和直角并与部分是与角度相关性质，如在圆周角中能轻易找到，，通过在图形中构造辅助圆往往能获得意想圆心角联系也比较紧密 三点及三点以上到同一点不到的效果，如果题目中出现了以下条件：距离相等，作辅助圆；同一侧有相等的角，或者需要构造出相等的角时，作辅助圆；若一个四边形的一组对角互补，则它的四个顶点共圆．在这些情况下，借助圆去解决一些问题都是非常好的一个选择，下面举例说明这三种构造辅助圆解题的模型应用。 二、典例精析 类型1 根据共端点等线段模型，根据圆的定义构造圆 1.如图，已知＝＝，且∠＝k∠，则∠是∠的（） A．2倍B．k倍C．2k D．1 【分析】由＝＝，得到A，B，C在以O为圆心的同一个圆上，则∠＝2∠，∠＝2∠，而∠＝k∠，即可得到∠＝k∠． 【解答】∵＝＝，∴A，B，C在以O为圆心的同一个圆上，如图，

1 / 14 ∠，∴∠＝2∠，∠＝2 ．B∠，∴∠＝∠＝k2k∠．故选：而∠＝k∠，即2 ，点F在边上，并且＝2，点C＝90°，＝6，＝8如图，在△中，∠2.到边距PP落在点E为边上的动点，将△沿直线翻折，点C处，则 点）离的最小值是（ ．以上都不对2.4 D1.2 C1.5 B．．A． 【分析】先依据勾股定理求得的长，然后依据翻折的性质可知＝，故依据垂线段最短可知当⊥为半径的圆上，2在以PF为圆心，以此点到的距离最短，然后依据题意画出图形，最后，利用相似三P时，点角形的性质求解即可． 【解答】如图所示：当∥．

2 / 14 ，，∴由勾股定理可求得＝10°，＝C＝906，＝8在△中，∵∠°．＝90由翻折的性质可知：＝＝2，∠＝∠C °．由垂线段最短可知此时有最小值．90∵∥，∴∠＝ 又∵为定值，∴有最小值． ，∠＝∠，∴△∽△．＝∠A又∵∠A ．3.2，解得：＝∴，即4/108 ．B2＝1.2．故选：∴＝﹣＝3.2﹣ ∠80°,则∠的度数为度如图2所示,在凸四边形中,3. 为圆心的同一个圆上，在以B，AC，D【解析】∵＝＝，得到,∠, ∠1/2∴∠1/2∠ =80°,∠∵∠∠+

构造辅助圆

构造辅助圆，交点立显现 在解一些几何问题时，常会遇到一些用常规方法很难解决的问题。这时，如果构造适当的图形来给以辅助，往往能促使问题转化，使问题中原来隐晦不清的关系和性质在新构造的环境中清晰地展现出来，从而简捷地解决问题，这种解题方法称为构造法。 对于在已知条件的线上找点与已知点构成一定的角的问题，如果能根据题目的题设和结论，构造出符合题意特征的辅助圆，即把题目中的固定角转化为圆的圆周角问题，就能使问题得以顺利解决，这种方法利用数形结合，使代数与几何等知识相互渗透，综合应用，它不但能较好的达到解题的目的，还有利于培养学生分析问题的能力。请看下面的两个例题：例1：（06东营）如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是 （A）3个（B）2个（C）1个（D）不存在 分析：要在直线l上找点P使∠APB=30°，可以构造以AB为边作等边三角形ABO，则∠AOB=60°，然后以O为圆心，AB为半径，作圆O，如图，∵△ABO为等边三角形∴OB∥l，∴点O到l的距离d

是【 C 】 A．0 B．1 C．2 D．3 分析：要使∠APE=90°，则需要以AE为直径作圆，如果此圆与线段BD相交，有几个交点，则使∠APE为直角的点P的个数就有几个，通过作图及圆心到直线的距离可知，以AE 为直径的圆与BD只有两个交点，所以使∠APE为直角的点P的个数是两个。 解：此题连接AE、AC、CE，因为矩形ABCG与矩形CDEF全等，所以Rt△ACG≌Rt△CEF 则∠ACE=90°，所以点C为满足条件的P点之一。取AE的中点O，然后以点O为圆心，以OA为半径作圆O，因为点O到BC的距离小于OC，所以圆O与BD有两个交点C、P，∵AE为直径，∴∠ACE=90°，∠APE=90°。∴使∠APE为直角的点的个数是两个。 综上所述，我们可以把某些与定点成定角的问题转化为圆周角问题，转化为直线与圆的位置关系问题，则能轻易加以解决。

辅助圆专题

辅助圆专题 一、 利用定义构造圆 1.如图，若PA=PB ，∠APB=2∠ACB ，AC 与PB 交于点P ，且PB=4，PD=3，则AD ·DC 等于( ) A ．6 B ．7 C ．12 D ．16 第1题图 第2题图 2. 如图，已知OA=OB=OC ，且∠AOB=k ∠BOC ，则∠ACB 是∠BAC 的( ) A ．k 21 倍 B ．是k 倍 C ．k 2 D ．k 1 二．三角形的外接圆 3. 如图，在△ABC 中，AB=AC ，任意延长CA 到P ，再延长AB 到Q ，使AP=BQ ，求证：△ABC 的外心O 与A ，P ，Q 四点共圆． 4. 如图，直线AB 和AC 与⊙O 分别相切于B 、C ，P 为圆上一点，P 到AB 、AC 的距离分别为4cm 、6cm ，那么P 到BC 的距离为 ． 三．四点共圆 5.同底同侧有相等顶角的三角形，则各顶点四点共圆（若能证明其两顶角为直角，即可肯定这四个点共圆，且斜边上两点连线为该圆直径。） 基本图形：

如图，在△ABC中，高BE、CF相交于H，且∠BHC=135°，G为△ABC内的一点，且GB=GC，∠BGC＝3∠A，连结HG，求证：HG平分∠BHF． 练习： 1 小明遇到一个问题： 如图，直线 l1∥l2∥l3， 试画一个等腰直角三角形ABC， 使其三个顶点分别在直线l1、l2、l3上 小明是这样思考的： 先在l1上任取一点A，作AN l3于N，在l1上截取AM=AN，连接MN ， MN与l2交于点B，连接AB，作△ABN的外接圆， 交l3于点C， △ABC即为所求. 2. 请你仿照上面的做法做出一个满足条件的等边三角形，使其三边分别在三条直线上

最新中考数学复习最值系列之辅助圆(一)

初中数学复习最值系列之辅助圆（一） 最值问题的必要条件是至少有一个动点，因为是动态问题，所以才会有最值．在将军饮马问题中，折点P就是那个必须存在的动点．并且它的运动轨迹是一条直线，解题策略就是作端点关于折点所在直线的对称即可． 当然，动点的运动轨迹是可以变的，比如P点轨迹也可以是一个圆，就有了第二类最值问题——辅助圆． 在这类题目中，题目很少直接告诉我们动点轨迹是个圆，也很少把这个圆画出来，因此，结合题目给的条件，分析出动点的轨迹图形，将是我们面临的最大的问题． 若已经确定了动点的轨迹圆，接下来求最最值的问题就会变得简单了，比如：如下图，A为圆外一点，在圆上找一点P使得P A最小． 已知圆轨迹类 【2017四川德阳】 如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A、B，且OA=OB，∠APB=90°，直线l不经过点C，则AB的最小值为________． 【分析】连接OP，根据△APB为直角三角形且O是斜边AB中点，可得OP是AB的一半，若AB最小，则OP最小即可． 连接OC，与圆C交点即为所求点P，此时OP最小，AB也取到最小值．

由定义构造辅助圆 圆的定义：平面内到定点的距离等于定值的所有点构成的集合． 构造思路：若动点到平面内某定点的距离始终为定值，则其轨迹是以定点为圆心、定值为半径的圆或圆弧． 【2014成都中考】 如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A'MN，连接A'C，则A'C长度的最小值是________． 【分析】考虑△AMN沿MN所在直线翻折得到△A'MN，可得MA'=MA=1，所以A'轨迹是以M点为圆心，MA为半径的圆弧． 连接CM，与圆的交点即为所求的A'，此时A'C的值最小． 构造直角△MHC，勾股定理求CM，再减去A'M即可．

从圆心角和圆周角的关系构造辅助圆

从圆心角和圆周角的关系构造辅助圆 通过圆的相关知识，我们可以得到以下结论：如果一个三角形有一个边长为固定值，且该边长的对角也为定值或其定值的补角，那么符合条件的三角形的外接圆是同一个圆。（如图） 利用这一结论，我们可以解决一些与固定角度有关的问题。 【例1】如图，正方形ABCD的中心为点O，面积为1989，点P为正方形内一点，满足∠OPB=45o，PA∶PB=5∶14，求PB的长。 【解析】因为∠OPB=45o，即∠OPB为以OB为弦的圆的圆周角，故OB所对的圆心角为90o，又点O为正方形的中心，所以该圆的圆心为AB的中点M， 如图，以M为圆心，MB为半径作圆，则点P必定在⊙M上。 AB为直径，所以∠APB=90o， 设AP=5x，则PB=14x， 故AB2=221x2=1989，解得x=3，所以PB=42.

【例2】如图，在平面直角坐标系中，A（-4，0），B（6，0），在y轴上是否存在点P，使得∠APB=45o？若存在，求出P的坐标；若不存在，说明理由。 【解析】P（0，±12）。 因为∠APB=45o，∠APB是以AB为弦的圆的圆周角，故AB所对的圆心角为90o，该圆的圆心M在AB的垂直平分线上，且△MAB为等腰直角三角形，∴M（1，±5）（如图）。 当M在第一象限时，过M作MN⊥y轴于点N， 则MN=1，N（0，5），MP=MA=5√2， ∴PN2=（5√2）2-1=49，PN=7，故P（0，12）； 同理，当M在第四象限时， P（0，-12）。 【例3】已知抛物线y=x2-2x-3与x轴交于点A、B，在直线y=2x+1上是否存在一点P使得∠APB=45o，如果存在，请写出点P的坐标，如果不存在，请说明理由。 【解析】易知A（-1，0），B（3，0），∴AB=4； ∵∠APB=45o，∴∠APB是以AB为弦的圆的圆周角，故AB所对的圆心角为90o，该圆的圆心M在AB的垂直平分线上，且∠AMB=90o；点P在优弧AB上。

中考数学必考几何模型：辅助圆

第十二章 辅助圆 模型1 共端点，等线段模型 图① O A C B 图② B O C A 图③ O A B C 如图①，出现“共端点，等线段”时，可利用圆定义构造辅助圆． 如图②，若OA ＝OB ＝OC ，则A 、B 、C 三点在以O 为圆心，OA 为半径的圆上． 如图③，常见结论有：∠ACB ＝12∠AOB ，∠BAC ＝1 2∠BOC . 模型分析 ∵OA ＝OB ＝OC . ∴A 、B 、C 三点到点O 的距离相等． ∴A 、B 、C 三点在以O 为圆心，OA 为半径的圆上． ∵∠ACB 是AB 的圆周角，∠AOB 是AB 的圆心角， ∴∠ACB ＝1 2∠AOB . 同理可证∠BAC ＝1 2 ∠BOC . （1）若有共端点的三条线段，可考虑构造辅助圆． （2）构造辅助圆是方便利用圆的性质快速解决角度问题． 模型实例 如图，△ABC 和△ACD 都是等腰三角形，AB ＝AC ，AC ＝AD ，连接BD ． 求证：∠1＋∠2＝90°. 2 1B C D A 证明 证法一：如图①，

∵AB ＝AC ＝AD ．∴B 、C 、D 在以A 为圆心，AB 为半径的⊙A 上． ∴∠ABC ＝∠2. 在△BAC 中，∵∠BAC ＋∠ABC ＋∠2＝180°,∴2∠1＋2∠2＝180°.∴∠1＋∠2＝90°. 证法二：如图②， ∵AB ＝AC ＝AD ．∴∠BAC ＝2∠1．∵AB ＝AC ， ∴B 、C 、D 在以A 为圆心，AB 为半径的⊙O 上． 延长BA 与圆A 相交于E ，连接CE ． ∴∠E ＝∠1．（同弧所对的圆周角相等．） ∵AE ＝AC ，∴∠E ＝∠ACE . ∵BE 为⊙A 的直径，∴∠BCE ＝90°． ∴∠2＋∠ACE ＝90°.∴∠1＋∠2＝90°. 图① 2 1C D A B 小猿热搜 1．如图，△ABC 为等腰三角形，AB ＝AC ，在△ABC 的外侧作直线AP ，点B 与点 D 关于AP 轴对称，连接BD 、CD ，CD 与AP 交于点E ．求证：∠1＝∠2． 1 2 P B A C E D A D 21 P E C B 证明 ∵A 、D 关于AP 轴对称，∴AP 是BD 的垂直平分线． ∴AD ＝AB ，ED ＝EB ．又∵AB ＝AC . ∴C 、B 、D 在以A 为圆心，AB 为半径的圆上．

决定孩子命运的八大关键问题

决定孩子命运的八大关键问题 你可以不是天才，但你可以是天才的父母！树立做父母正确的家庭教育观念，为孩子建造一个良好的人生平台，让孩子有很好的人格修养，懂得做人，懂得成功的真正含义。简单方便，容易操作，适合于每一位孩子家长。 在孩子的成长中，高分数、好成绩并不代表一切。事实上，一些决定孩子命运的关键问题常常被我们忽略，它们才是孩子未来的保障。父母的目光不能只盯在暂时的成绩上，孩子要进行的是一场人生的、持久的接力赛，谁笑到最后，谁笑得最好!只有解决了教育的关键问题，才能找到正确的发展方向，才能积蓄竞争力，打好持久战! 身为现代父母，您知道现代孩子该怎样教育吗？很多父母认为，家庭教育就是开发孩子的智力，也就是让孩子从两三岁开始背唐诗，四五岁学英语，上学后要请家教、上辅导班，成绩一定要名列前茅，将来一定要上名牌大学。似乎只有这样，父母的教育才算成功，孩子才算成才。实践证明，这是对家庭教育的极大误解，是升学教育在家庭教育中产生的不良后果。家庭教育最重要的任务应该是建筑孩子的人格长城。 在孩子的成长中，高分数、好成绩并不代表一切。事实上，一些决定孩子命运的关键问题常常被我们忽略，它们才是孩子未来的保障。 试想，如果一个孩子缺少对生命的认知(一遇到挫折就产生轻生的念头 )，没有梦想的能力(自己将来想做什么都不知道)，不懂得保护自己(做了博士生依然被农民拐卖)，无法与别人共享(腰缠万贯却不快乐)，那么，即使这个孩子门门功课考第一，又能怎么样？ 当今，最该改变的是父母，是父母的教育观念。那么，正确的家庭教育应该是什么？是父母应该帮助孩子建造一个良好的人生平台，让孩子有很好的人格修养，懂得做人，懂得成功的真正含义。 只有父母的教育观念发生了转变，我们的孩子才能接受良好的家庭教育，才能终生受益。 这8个关键问题之所以关键，是因为它往往会在紧要关口成为孩子前进和幸福的羁绊。现在让我们赶紧来看看吧！ 第—大关键问题如何让孩子树立乐观向上的心态 1．接受现实是走向乐观的第一步 2．培养乐观的性格，让孩子坦然地面对生活中的不幸 3．让孩子保持一颗平常心

12第十二章 辅助圆 (1)

3 图2图B C O A B C O A A B C O 图11 2 B A D 1 2C P E D B A B C A D 第十二章 辅助圆 模型1 共端点，等线段模型 模型分析 （1）若有共端点的三条等线段，可考虑构造辅助圆； （2）构造辅助圆是方便利用圆的性质快速解决角度问题。 模型实例 例1．如图，△ABC 和△ACD 都是等腰三角形，AB=AC ，AC=AD ，连接BD 。 求证：∠1+∠2=90°。 热搜精练 1．如图，△ABC 为等腰三角形，AB=AC ，在△ABC 的外侧作直线AP ，点B 与点D 关于AP 轴对称，连接BD 、CD ，CD 与AP 交于点E 。求证：∠1=∠2。 2．已知四边形ABCD ，AB ∥CD ，且AB=AC=AD=a ， BC=b ，且2a>b ，求BD 的长。

C A B D B A C D B A C D 2 图图1B C O A O D 模型2 直角三角形共斜边模型 模型分析 （1）共斜边的两个直角三角形，同侧或异侧，都会得到四点共圆； （2）四点共圆后可以根据圆周角定理得到角度相等，完成角度等量关系的转化，是证明角相等重要的途径之一。 模型实例 例1．如图，AD 、BE 、CF 为△ABC 的三条高，H 为垂心，问： （1）图中有多少组四点共圆； （2）求证：∠ADF=∠ADE 。 E B C A D H F

E B C A D F E B C A D G F E B C A D H F 例2．如图，E 是正方形ABCD 的边AB 上的一点，过点E 作DE 的垂线交 ∠ABC 的外角平分线于点F 。求证：EF=DE 。 热搜精练 1．如图，锐角△ABC 中，BD 、CE 是高线，DG ⊥CE 于G ，EF ⊥BD 于F 。 求证：FG ∥BC 。 2．如图，BE 、CF 为△ABC 的高，且交于点H ，连接AH 并延长交BC 于点D 。 求证：AD ⊥BC 。

初中数学 构造辅助圆探求最值问题

构造辅助圆探求最值问题 最值问题是中考舞台上的常青树，涉及知识面广，解决的方法活，且富有一定的技巧，所以 倍受命题老师的青睐.下面就谈谈辅助圆在求最值时的精彩，供学习时借鉴. 1.构造辅助圆直接求线段的最小值 例1 如图1，Rt △ABC 中，AB ⊥BC ，AB=6，BC=4，P 是△ABC 内部的一个动点，且满足∠ PAB=∠PBC ，则线段CP 长的最小值为 （ ） A.32 分析：如图1，根据已知条件，我们不难发现，动点P 在以AB 为直径的圆上运动，而点C 在辅助圆的外部，根据点与圆的关系，知道，当O,P ，C 三点共线时，CP 最短. 解：因为∠PBA+∠PBC=90°，∠PAB=∠PBC ，所以∠PBA+∠PAB=90°，所以∠APB=90°，所 以点P 在以AB 为直径的圆上，当O,P ，C 三点共线时，CP 最短，因为AB=6,所以OB=3,因为 BC=4，所以OC=5，所以CP=OC-OP=5-3=2,所以CP 的最小值为2，所以选B. 点评：构造辅助圆，把不容易确定的线段的最小值问题转化为点与圆的关系是解题的关键， 要学会这门技巧. 2.构造辅助圆间接求线段的最小值 例2 如图2，菱形ABCD 的边AB=8，∠B=60°，P 是AB 上一点，BP=3，Q 是CD 边上一动点， 将梯形APQD 沿直线PQ 折叠，A 的对应点为A ′，当CA ′的长度最小时，CQ 的长为 （ ） A. 5 B. 7 C. 8 D.132

分析：如图2，当点Q在运动时，不难发现点A的对称点A'在以P为圆心，PA为半径的圆上，由BP=3，知道PA=5，连接PC与圆交于点F，由点C是圆P外的一点，根据点与圆的关系知道，当A'与点F重合时，CF=C A'最短，找到了最短位置，接下来就是求CQ的数值了. 根据图形的对称性知道：∠QPA=∠CPQ，根据菱形的性质，知道：AB∥CD，所以∠QPA=∠CQP，所以∠CPQ=∠CQP，，所以CQ=CP.过点C作CE⊥AB，垂足为E，根据三角形ABC 是等边三角 形，且AB=8，所以,因为BP=3，所以EP=1，在直角三角形CEP中， =所以CQ=7. 解：选B. 点评：巧妙把线段的最小值转化成圆外一点与圆的关系是解题的关键，也是一种常用的方法，希望平时学习时多加练习. 3.直接应用给定的半圆，探求最值 例3 如图3，在△ABC中，AB=10,AC=8,BC=6,以边AB的中点O为圆心，作半圆与AC相切，点P,Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值和最小值的和是（） 32 3

中考专题：构造辅助圆巧解题

构造辅助圆巧解题 例1、如图，已知O 是四边形ABCD 内一点，OA=OB=OC ，∠ABC=∠ADC=70°，则∠DAO+∠DCO= ° 变式1：如图所示，在四边形ABCD 中，AB=AC=AD ，∠BAC=26°，∠CAD=74°，则∠BDC=____°，∠DBC=____° 变式2：如图，在四边形ABCD 中，AD ∥BC ，AB=AC=AD=2.5，CD=3，求BD 的长。 例2、如图，在Rt △ABC 中，∠ACB=90°，∠A=30°，AC=34，BC 的中点为D ，将△ABC 绕点C 顺时针旋转任意一个角度得到△FEC ，EF 的中点为G ，连接DG ，在旋转过程中，DG 的最大值为 。 变式1：如图，在Rt △ABC 中，∠ACB=90°，∠A=30°，AC=34，BC 的中点为D ，将△ABC 绕点C 顺时针旋转 任意一个角度得到△FEC ，G 为线段EF 上的一个动点，连接DG ， 在旋转过程中，DG 的最小值为 ，最大值为 。 变式2：在△ABC 中，AB=AC=5，BC=6，将△ABC 绕点C 顺时针旋转，得到△A 1B 1C ，点E 是BC 上的中点，点F 为线段AB 上的动点，在△ABC 绕点C 顺时针旋转过程中，点F 的对应点是F 1，求线段EF 1长度的最大值与最小值的差。 D D 1

例3、在平面直角坐标系中，已知点A(4，0)，点B(-6，0)，点C 是y 轴上的一个动点，当 ∠BCA=45°时，求点C 的坐标。 变式1：在平面直角坐标系中，已知点A(33，0)，点B(3-，0)，点C 是y 轴上的一个动点，当∠BCA=30°时，则点C 的坐标是 。 变式2：在平面直角坐标系中，已知点A(33，0)，点B(3-，0)，点C 是y 轴上的一个动点，当∠BCA=120°时，则点C 的坐标是 。 变式3：（2016毕业生水平考试第24题） 24．抛物线c bx x y ++- =2 2 1过点A(0，1)，B(4，3)，过点B 作BD ⊥x 轴于点D 。 (1)试求该抛物线顶点P 的坐标； (2)过点D 作直线l ，将四边形AODB (3)在坐标轴上是否存在点M ，使得∠

巧作辅助圆解决问题

巧作辅助圆解决问题 在近几年中考试卷中，常出现这样一类题目，从表面上看是一个三角形或四边形问题，用三角形或四边形的知识来解决非常困难，甚至根本无法解决，但我们可以从已知条件中发现蛛丝马迹，也就是发现图形中的隐含特征，从而通过构造辅助圆，借助圆的知识来解决问题这样的问题一般具有以下特征 一、到定点的距离等于定长 例1如图1，在正方形ABCD外侧作直线DE，使45°＜∠CDE＜90°，点C关于直线DE的对称点为M，连接CM，AM，其中AM交直线DE 于点N，若MN＝4，AN＝3，则正方形ABCD的边长为( )。 A. B.5 C.5 D. 解析:如图2，连接DM，由于点C、M关于直线DE 对称,故直线DE垂直平分线段CM，因而DC＝DM. 四边形ABCD是正方形，故DA＝DC＝DM，即点A、 C、M到点D的距离相等，根据这一特征，我们可 以想到，以点D为圆心，DA的长为半径画圆，则 点C、M必在⊙D上.由∠ADC＝90°，可得∠AMC＝45°.连接CN，则CN＝MN＝4，故∠MCN＝∠AMC＝45°，从而∠ANC＝90°，连接AC，我们不难求出AC＝，选D。 点评:随着直线DE位置的变化，点M的位置也在变化，但它一定在

以点D为圆心，DA的长为半径的圆上，这就是运动变化中的不变关系，解决这类问题的关键是抓住“A、C、M三点到点D的距离相等”这一特征，但这个特征比较隐蔽，不容易发现，要综合考虑本题中的所有条件，而且要有一定的洞察力和解题经验.事实上，这类问题中的隐含条件往往都不是一眼就能看出来的。 二、张角为直角 例2如图3，在等腰R△ABC中，∠BAC=90o，AB=AC，BC=2，点D 是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段 CE长度的最小值为（）。 A、2-2 B、 C、-1 D、-1 解析：本题中点D在动，直径AD的大 小在变，线段BD在动，点E也在动，运 动变化中有不变的量吗?有！如图4，连 接AE，由于AD为直径，故∠AED的大 小保持不变，为直角，从而∠AEB始终 为直角，∠AEB的两边经过线段AB的两 个端点，我们不妨称∠AEB为线段AB所 对的张角。 本题中，虽然点E是一个动点，但线段AB所对的张角(∠AEB)在运动过程中始终为直角。作R△ABE的外接圆，其圆心为斜边AB

构造辅助圆巧解三角形问题

构造辅助圆巧解三角形问题 在解决三角形相关问题时，有时常规方法求解难度大，技巧性强，且不易奏效，但若 能针对题目的本质特征，恰当地构造辅助圆，巧妙地运用圆的有关知识，则可起到化隐为显、化难为易、化繁为简的作用，使复杂的问题迎刃而解．下面结合实例谈谈构造辅助圆在巧解三角形问题中的应用，希望给大家以启示， 一、构造辅助圆求三角形的面积 例1 如图l ，已知AB=AC=BC=AD ，AE 平分∠CAD ，CE ⊥BC ，AE =3，BD =5，则 ABC S ?=__________. 解 AB=AC=AD ，∴点B 、C 、D 在以A 为圆心， AB 为半径的圆上(如图1). CE ⊥BC ，∠ACB=60°，∴∠ACE=30°. 又 ∠BDC=21 ∠BAC=30°， ∴∠ACE=∠BDC. AE 平分∠CAD ，∴∠CAE=21 ∠CAD ∠DBC=21∠CAD ， ∠CAE=∠DBC ，△ACE ∽△BDC ， BC AE BD AC = ∴ AC=BC ， BD AE BC ?=∴2 ． ABC S ?=243BC ，∴ABC S ?=3 41543=?BD AE . 评注 本题主要考查了圆的性质、相似三角形的性质与判定以及三角形的面积公式．由条件AB=AC=AD ．自然联想到构造辅助圆⊙A ，从而得到∠BDC=30°，其中由△ACE ∽△BDC 得出BC2 = BD AE ?是求解的关键． 二、构造辅助圆求三角形的内角 例2 如图2，已知AD 、AE 、AM 分别为△ABC 的BC 边上的高、角平分线、中线，且∠1=∠2，则∠BAC=____°．

解 作△ABC 的外接圆交AE 延长线于点N ，连结MN ，BN ，CN. ∠BAE=∠CAE ， ∴BN ⌒ =CN ⌒ ，则BN=CN. 又 MB=MC ，∴MN ⊥BC ．而 AD ⊥BC ，∴MN ∥AD ， 于是∠ANM=∠l=∠2，故MA=MN. ∴点M 是弦BC 、AN 的中垂线的交点，即M 为圆心． 又BC 为直径，∴∠BAC=90°. 评注 此题若直接求∠BAC 的度数很难达到目的，而通过构造△ABC 的外接圆之后，可充分利用等腰三角形及圆的相关性质，说明点M 是外接圆的圆心，又因BC 为直径，从而得出∠BAC=90°，问题得以巧妙解决． 三、构造辅助圆求三角形的高 例3 如图3，已知在△ABC 中，CD ⊥AB 于D ，∠ACB=45°，AD =2，BD =3，求CD 的长． 解 作△ABC 的外接圆⊙O ，连结AO ，BO ，CO. 过点D 作OE ⊥AB 于点E ，OF ⊥CD 于点F ． ∠ACB=45°， ∴∠AOB=90°， ∴△AOB 是等腰直角三角形. AB=AD+BD=5，∴OC=OB=225，OE=DF=25 ． 又 DE=AE - AD=21，∴OF=21 ． 在Rt △COF 中，由勾股定理，得CF=27 ，∴CD=CF+DF=6． 评注 由于AB 的长及∠ACB=45°是确定的，可联想构造出△ABC 的外接圆⊙O ．于是得到△AOB 是等腰直角三角形，再利用勾股定理问题便得以顺利解决，当然本题还有其它解法，其中构造辅助圆应是一种比较巧妙的解法． 四、构造辅助圆求三角形的边长 例4 知图4，已知1?，2?， 3 ?同一平面内的三条平行直线，1?与2?的距离是l ，2?与 3 ?的距离是2，等边△ABC 的三个顶点分别在1?，2?，3? 上，则等边△ABC 的边长为______。

构造辅助圆专题

构造辅助圆专题 1、在平面直角坐标系中，A （4,0），O 为原点，求直线3y x =-+上一点P ，使△AOP 为等腰三角形，这样的点P 有几个？ y O x 2、如图，:33l y x =+交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线交x 轴于另一点C （3,0）. （1）求抛物线的解析式 （2的点Q 的坐标.

3、已知：如图，在□ EFGH 中，点F 的坐标是（-2，-1），∠EFG=45°． （1）求点H 的坐标; （2）抛物线1C 经过点E 、G 、H ,现将1C 向左平移使之经过点F ，得到抛物线2C ,求抛物线2C 的解析式； （3）若抛物线2C 与y 轴交于点A ，点P 在抛物线2C 的对称轴上运动．请问：是否存在以AG 为腰的等腰三角形AGP ？若存在，求出点P 的坐标；若不存在，请说明理由． 4、如图所示，在四边形ABCD 中，AB=AC=AD ，∠BAC=26?，∠CAD=74?，则BDC ∠=________°，DBC ∠=________° 5、在平面直角坐标系中，已知A （2，2），B （2，-3），点P 在y 轴上，且△AB P 为直角三角形. 请问满足条件的点P 有几个？ 并求出它们的坐标. D C B A

D C B A 6、如图所示，在凸四边形ABCD 中，AB=BC=BD, ?=∠80ABC ， 则ADC ∠的度数为 . 7、已知如图，梯形ABCD 中，AB ⊥BC 于B,CD ⊥BC 于C （1）当AB=4，CD=1，BC=4时，点P 在直线BC 上，且?=∠90APD ，这样的点有 个. （2）设AB=a ，DC=b ，AD=c ，点P 在直线BC 上，且?=∠90APD ，试确定此时a ，b ，c 满足的关系式. 8、如图，矩形ABCG （AB ＜BC ）与矩形CDEF 全等，点B 、C 、D 在同一条直线上，∠APE 的顶点P 在线段BD 上移动，使∠APE 为直角的点P 的个数是（ ） A ．0 B ．1 C ．2 D ．3 9、平面直角坐标系xOy 中，抛物线244y ax ax a c =-++与x 轴交于点A 、点B ，与y 轴的正半轴交于点C ，点 A 的坐标为(1, 0)，OB =OC ，抛物线的顶点为D ． (1) 求此抛物线的解析式； (2) 若此抛物线的对称轴上的点P 满足∠APB =∠ACB ，求点P 的坐标； A B D E F G P C

江苏省徐州市201x年中考数学总复习提分专练08构造辅助圆习题

提分专练(八)构造辅助圆 |类型1| 根据圆的定义构造圆 1.如图T8-1,已知OA=OB=OC,且∠AOB=k∠BOC,则∠ACB是∠BAC的倍. 图T8-1 2.如图T8-2所示,在凸四边形ABCD中,AB=BC=BD,∠ABC=80°,则∠ADC的度数为. 图T8-2 3.如图T8-3,在四边形ABCD中,AB=AC=AD,∠BAC=25°,∠CAD=75°,则∠BDC= °,∠DBC= °. 图T8-3 4.[xx·淮安]如图T8-4,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF 沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是.

图T8-4 |类型2| 三角形的外接圆 5.如图T8-5,矩形ABCG与矩形CDEF全等,AB=1,BC=3,点B,C,D在同一条直线上,∠APE的顶点P在线段BD上移动, 使∠APE为直角的点P的个数是() A.0 B.1 C.2 D.3 6.已知:如图T8-6,直尺的宽度为2,A,B两点在直尺的一条边上,AB=6,C,D两点在直尺的另一条边上.若∠ACB=∠ ADB=90°,则C,D两点之间的距离为. 图T8-6 7.如图T8-7,已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是边AB上的动点,Q是边BC上的动点,且∠CPQ=90°,则线段CQ的取值范围是. 图T8-7 8.已知平面直角坐标系中两定点A(-1,0),B(4,0),抛物线y=ax2+bx-2过点A,B,顶点为C,点P(m,n)为抛物线上一点,其中n<0. (1)求抛物线的解析式和顶点C的坐标; (2)当∠APB为钝角时,求m的取值范围.