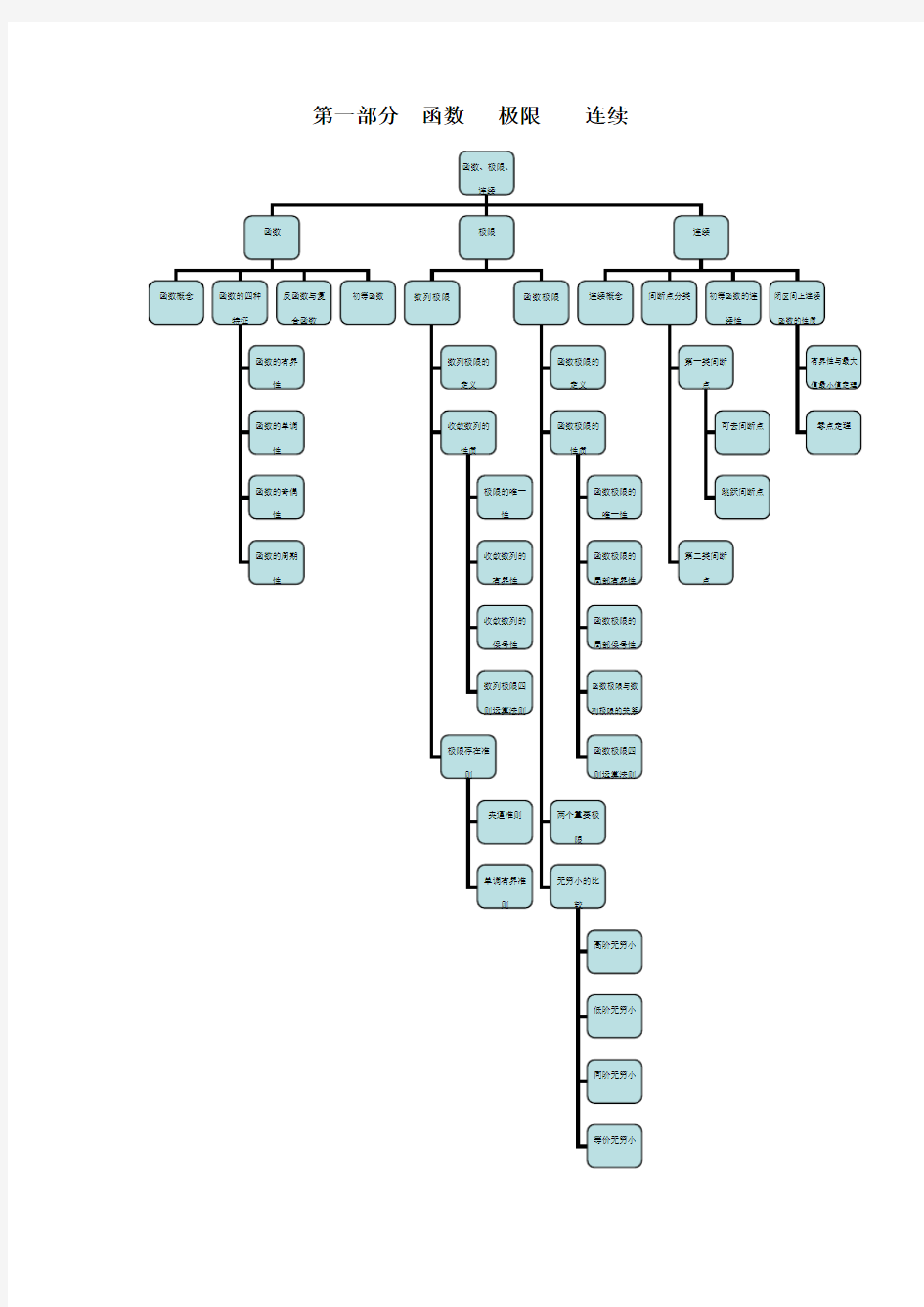
第一部分函数极限连续
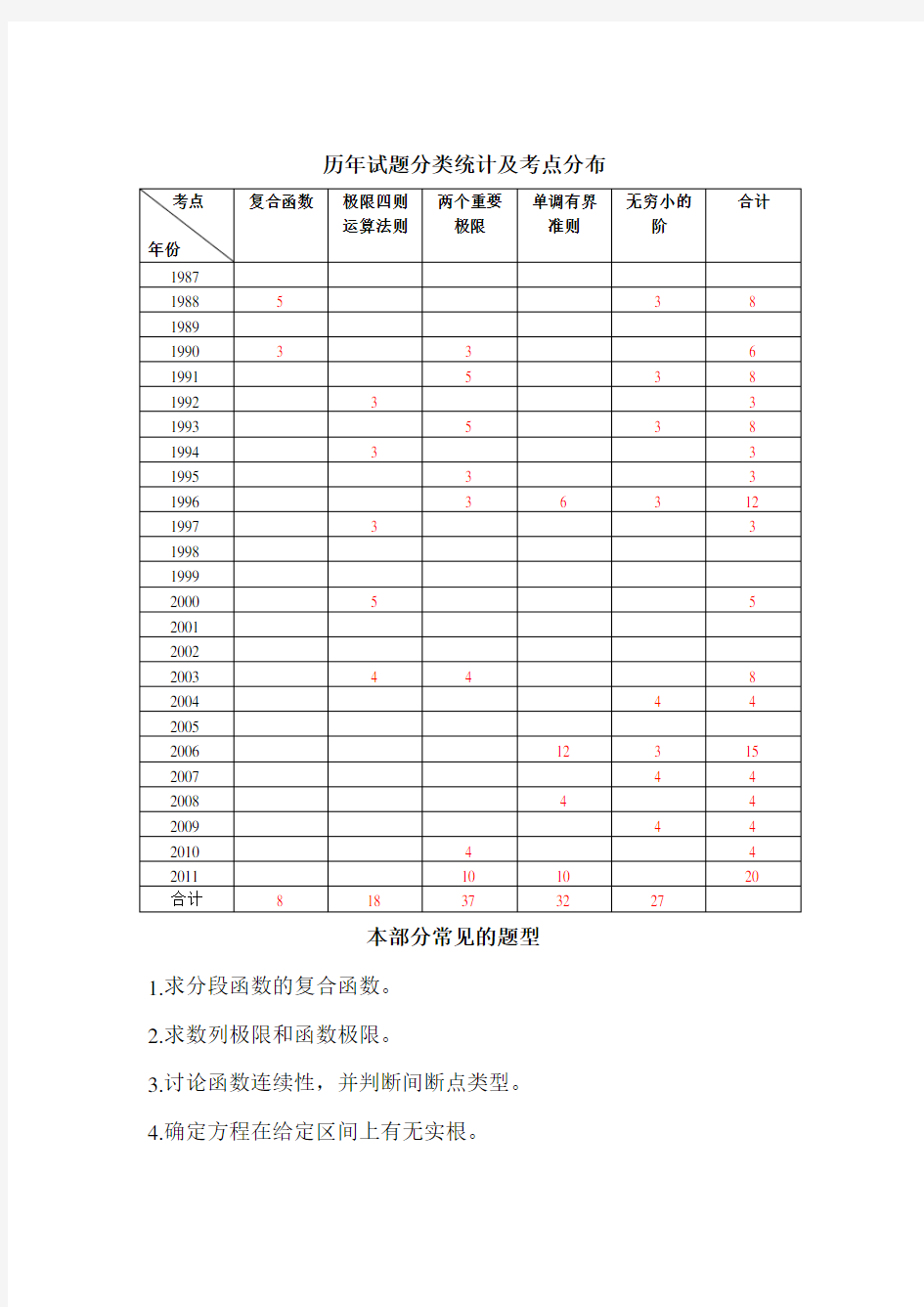
历年试题分类统计及考点分布
本部分常见的题型
1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性,并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数
例1 (1988, 5分) 设2
(),[()]1x f x e f x x ?==-且()0x ?≥,求()x ?及其定义域。
解: 由2
()x f x e =知2
()[()]1x f x e x ??==-,又()0x ?≥,
则()0x x ?=≤.
例2 (1990, 3分) 设函数1,1
()0,1
x f x x ?≤?=?>??,则[()]f f x =1.
练习题: (1)设 1,1,
()0,1,(),1,1,
x x f x x g x e x ?
===??
->?求[()]f g x 和[()]g f x , 并作出这
两个函数的图形。 (2)
设
20,0,0,0,
()(),
,0,,0,
x x f x g x x x x x ≤≤??==??>->??求
[()],[()],[()],[()]f f x g g x f g x g f x .
二、 求数列的极限
方法一 利用收敛数列的常用性质
一般而言,收敛数列有以下四种常用的性质。
性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。 性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。 性质3(收敛数列的保号性) 如果lim n n x a →∞
=,且0a >(或0a <),那么存在
0n N +∈,使得当0n n >时,都有0n x >(或0n x <).
性质4(数列极限的四则运算法则) 如果,,lim lim n n n n x a y b →∞
→∞
==那么
(1)()lim n n n x y a b →∞
±=±;
(2)lim n n n x y a b →∞
?=?;
(3)当0()n y n N +≠∈且0b ≠时,lim
n n n x a y b
→∞
=.
例3 若
lim n
n x
a →∞
=,则
lim n
n x
a →∞
=.
注: 例3的逆命题是不对的, 例如我们取(1)n n x =-, 显然1lim n n x →∞
=,
但数列(1)n n x =-没有极限。
例4 如果数列{}n x 收敛, 那么数列{}n x 一定有界。
注: 例4的逆命题是不对的, 例如我们取(1)n n x =-, 显然数列{}n x 有界, 但数列(1)n n x =-没有极限。
例5 设{}{}{},,n n n a b c 均为非负数列, 且0,1,lim lim lim n n n n n n a b c →∞
→∞
→∞
===+∞.
下列陈述中哪些是对的, 哪些是错的? 如果是对的, 说明理由;如果是错的, 试给出一个反例。
(1) ,n n a b n N +<∈; (2) ,n n b c n N +<∈; (3)
lim n n
n a c
→∞
不存在; (4)
lim n n
n b c
→∞
不存在.
解: (1)是错的, 我们可以令1,1n n n
a b n
n ==+, 显然0,1lim lim n n n n a b →∞→∞
==, 但111
1,2
a b ==, 从而11a b >.
(2)是错的, 我们可以令1
,13
n n n b c n n =
=+, 显然
1,lim lim n n n n b c →∞→∞
==+∞, 但1111
,23b c ==, 从而11b c >. (3)是错的, 我们可以令1
1,3
n n a c n n ==, 显然0,lim lim n n n n a c →∞
→∞
==+∞,
但111()33
lim lim n n n n a c n n →∞
→∞
=?=.
(4)是对的, 由于10,lim lim n n n n b c →∞
→∞
=≠=+∞, 则lim n n n b c →∞
=+∞, 即极
限lim n n n b c →∞
不存在。
注1: 极限的保序性是说, “若,,lim lim n n n n a a b b a b →∞
→∞
==>, 则存在0n N +
∈
使得当0n n >时有n n a b >.”, 而不是对任意的n N +∈有n n a b >. 注2: 事实上我们可以得到如下一个常用的结论:
若0,lim lim n n n n a a b →∞
→∞
=≠=∞, 则lim n n n a b →∞
=∞.
练习题: 设数列{}n x 与{}n y 满足0lim n n n x y →∞
=, 则下列断言正确的是( )
(A) 若{}n x 发散, 则{}n y 必发散. (B) 若{}n x 无界, 则{}n y 必无界. (C) 若{}n x 有界, 则{}n y 必为无穷小. (D) 若1n x ??????
为无穷小, 则{}n y 必为无穷小. 方法二 利用一些常用的结论
(1) 设数列{}n x 有界, 又0lim n n y →∞
=, 则0lim n n n x y →∞
=.
(2) 0,10(1),1,1,1
lim lim n
n n n q q q q q q →∞→∞?
+∞>?.
(3)
11(0)lim n
n a
a →∞
=>.
例6
1cos 2lim n n n
π→∞=0. 练习题:
(1)1)sin
2
lim n n π
→∞
=_______.
(2)1)sin
2
lim n n π
→∞
=__________. 例7
1()lim n
n
n n
n a
b c →∞
++={}max ,,a b c (0,0,0a b c ≥≥≥).
解: 由于{}{}11max ,,()3max ,,n
n
n n n a b c a b c a b c ≤++≤,故1()lim n
n
n n
n a b c →∞
++=
{}max ,,a b c .
练习题: 已知10,......,0m a a ≥≥, 求极限11
(......)lim n n n
m n a a →∞
++.
例8
2211lim n
n n x x x
→∞-=+,10,1,1
x x x x x ?
=??
->?. 解: 当1x <时 2211lim n
n
n x x x x →∞
-=+; 当1x =时 22101lim n
n
n x x x
→∞-=+; 当1x >时
2222111111lim lim n
n n
n n n
x
x x x x x x →∞→∞
--==-++. 故
2211lim n
n n x x x
→∞-=+,1
0,1,1
x x x x x ?
=??
->?. 练习题:
211lim n
n x
x
→∞+=+________. 方法三 利用Heine 定理将抽象数列的极限转化为具体函数的极限 Heine 定理:
()lim x x f x A →=的充分必要条件是: 对于任意满足条件
0lim
n n x x →∞
=且0()n x x n N +
≠∈的数列{}n x , 相应的函数值数列{}()n f x 成立()lim n
n f x A →∞
=.
例9 设数列{}n x 满足0()n x n N +≠∈且0lim n n x →∞=, 计算2
1
sin ()lim n x n n n x x →∞
. 解: 我们考虑函数极限
2
2
2
2
3
2
sin sin sin ln()ln(11)11
sin cos 1
300
sin ()lim lim lim lim lim lim x
x
x
x x x x x x x x x x x
x x x x x x x x e e
e
e
e
x +
----→→→→→→=====
sin 166
lim x x
x e
e --
→==
从而22
1
1
160
sin sin ()()lim lim n x n x n x n x x e x x -→∞→==.
练习题: 设数列{}n x 满足0()n x n N +>∈且0lim n n x →∞=,计算1
ln(1)[]lim n
x n n n
x x →∞+.
方法四 利用夹逼准则 例10 计算222111
(
......)2lim n n n n n n πππ
→∞
++++++. 解: 由于2222222111(......)2n n n n n n n n n n πππππ
≤+++≤+++++, 故
222111
(
......)12lim n n n n n n πππ
→∞
+++=+++. 练习题: (1)
计算......lim n →∞
++
.
(2) 计算22212(
......)12lim n n
n n n n n n n
→∞
+++++++++.
(3) 计算1
111(1......)23lim n n n →∞
++++.
(4)
计算......lim n →∞
+. 方法五 利用单调有界准则
适用题型: (1)由递推关系1()n n x f x +=定义的数列{}n x 极限问题, 一般先用单调有界准则证明极限存在, 然后等式两边取极限求出极限。 (2)有些题目直接给出了数列{}n x 的通项公式, 要求我们证明数列{}n x 的极限存在, 这时优先考虑用单调有界准则证明其极限存在。
例11 (1996, 6分)
设1110,)n x x n N ++==∈, 试证数列{}n x 极限存在, 并求此极限。
证明: 先证明数列{}n x 是单调减少的。
由于10()n n n x x x n N ++-==≤?∈, 所以数列{}n x 是单
调减少的。
注意到10()n x x n N +≤≤?∈, 于是数列{}n x 有界, 故数列{}n x 极限存在。设lim n n x a →∞
=, 等
式1n x +=两边取极限
得a =, 即3a =或
2a =-, 又1010a x ≤≤=, 所以3a =, 亦即3lim n n x →∞
=.
练习题: (1)
的极限存在, 并求此极限。
(2)
设11)n x x n N ++=∈, 试证数列{}n x 极限存在, 并求此极限。
(3)
设111,)n x x n N ++==∈, 试证数列{}n x 极限存在, 并求此极限。
(4) 设1101,(2)()n n n x x x x n N ++<<=-∈, 试证数列{}n x 极限存在, 并求此极限。
例12 (2008, 4分) 设函数()f x 在(,)-∞+∞内单调有界, {}n x 为数列, 下列命题正确的是( B )
( A ) 若{}n x 收敛, 则{}()n f x 收敛. ( B ) 若{}n x 单调, 则{}()n f x 收敛. ( C ) 若{}()n f x 收敛, 则{}n x 收敛. ( D ) 若{}()n f x 单调, 则{}n x 收敛.
解: 由于()f x 在(,)-∞+∞上单调有界, 若{}n x 单调, 则{}()n f x 是单调有界数列, 故{}()n f x 收敛。
事实上(A)、(C)、(D)都是错误的。若令(1)()n
n x n N n
+-=∈, 显然(1)0lim n
n n →∞-=, 即{}n x 收敛, 再令1arctan ,0()arctan ,0
x x f x x x +≥?=?
-∞+∞上单调有界,
但{}()n f x 不收敛。由于
11arctan ,2()()1arctan(),21()
n n k k N n
f x n k k N n ++?+=∈??=??-=-∈??
, 所以()lim n n f x →∞不存在, 故(A)不正
确。
若令(),()arctan n x n n N f x x +=∈=, 显然{}()n f x 收敛且单调, 但{}n x 不收敛, 故(C)和(D)不正确。
例13 (2006, 12分) 设数列{}n x 满足110,sin ()n n x x x n N π++<<=∈. ( I )证明lim n n x →∞
存在, 并求该极限;
( II )计算21
1()lim n x n n n x
x +→∞
.
解: ( I )用数学归纳法证明数列{}n x 是单调减少的且有界。 由10x π<<得2110sin x x x π<=≤<;
设0n x π<<, 则10sin n n n x x x π+<=≤<, 所以数列{}n x 是单调减少的且有界, 故lim n n x →∞存在。
记
lim n
n x
a →∞
=, 于是0a π≤≤.由1sin n n x x +=得sin a a =, 注意到函数
()sin f x x x =-在区间[0,]π上是单调增加的, 所以0a =, 即0lim n n x →∞
=.
( II )见例9.
注1: 在判别一个函数()f x 的单调性时, 我们经常用到下面两个孰知的结论。
(1) 设函数()f x 在[,]a b 上连续, 在(,)a b 内可导, 若(,)a b 中除至多有限个点有'()0f x =之外都有'()0f x >, 则()f x 在[,]a b 上单调增加。
(2) 设函数()f x 在[,]a b 上连续, 在(,)a b 内可导, 若(,)a b 中除至多有限个点有'()0f x =之外都有'()0f x <, 则()f x 在[,]a b 上单调减少。
注2: 记住一些基本的不等式可以帮助考研学子在考试时节省大量的时间, 例如sin (),ln(1)(0)x x x R x x x ≤?∈+等。 练习题: 设数列{}n x 满足110,ln(1)()n n x x x n N ++>=+∈. ( I )证明lim n n x →∞
存在, 并求该极限;
( II )计算1
1()lim n x n n n x
x +→∞
.
例14 (2011, 10分) 证明: (1)对任意正整数n , 都有
111ln(1)1n n n
<+<+; (2)设111......ln ()2
n x n n N n
+=+++-∈, 证明数列{}n x 收敛。
证明: (1)由于函数()ln(1)f x x x =-+在[0,)+∞上单调增加, 从而当0x >时()(0)0f x f >=, 所以对任意正整数n , 都有1
1ln(1)n
n
+<.
由于函数()ln(1)1
x
g x x x =+-
+在[0,)+∞上单调增加, 从而当0x >时()(0)0g x g >=, 所以对任意正整数n , 都有11
ln(1)1n n
<++.
故对任意正整数n , 都有111ln(1)1n n n
<+<+. (2)先证明数列{}n x 是单调减少的。
我们考虑 11111
[1......ln(1)](1......ln )212n n x x n n n n
+-=+++
-+-+++-+ 11
ln(1)0()1n N n n
+=
-+
1131
1......ln ln 2ln ......ln(1)ln ln(1)ln 0()
22n x n n n n n N n n
+=+++->++++-=+->?∈从而数列{}n x 有界, 故数列{}n x 收敛。 练习题: 设22111......()2n x n N n
+
=+
++∈, 证明数列{}n x 收敛。 方法六 利用定积分的定义
设函数()f x 在[,]a b 上连续, 则11[()]()lim b
n n i a
i
f a b a f x dx n n →∞=+-=∑?.
例15 计算极限111
(
......)122lim n n n n
→∞
+++++. 解:
1
011111111
(......)(......)ln 21212211111lim lim n n dx n n n n x n n
→∞→∞+++=+++==++++++
?. 例16 (1998, 6分) 求2sin
sin
sin lim(......)11
12n n n n n n n
π
π
π→∞+
+++++. 解: 注意到
11111sin sin sin 11n n
n i i i i i i n n n n n i
πππ
===≤≤++
∑∑∑ 而
1
1
012lim sin sin n n i i xdx n n πππ→∞===∑?,
1
1
10112
lim sin lim(sin )sin 11n n n n i i i n i xdx n n n n n ππππ→∞→∞===?==++∑∑?
故2sin
sin
sin 2lim(......)1112n n n n n n n
π
π
ππ→∞+
++=+++
. 练习题: (1)
计算1
1lim n n i n →∞= (2) 计算1
12......(0)lim p p p
p n n p n +→∞
+++>. (3) 计算12(1)[sin sin
......sin ]lim n n n
n
n n
π
ππ→∞
-+++. 三、 求函数的极限
方法一 利用函数极限的常用性质
一般而言,函数极限有以下四种常用的性质。
性质1(函数极限的唯一性) 如果0
lim ()x x
f x →存在,那么这极限唯一。 性质2(函数极限的局部有界性) 如果0
lim ()x x
f x A →=,那么存在常数0
M >和0δ>,使得当00x x δ<-<时,有()f x M ≤.
性质3(函数极限的局部保号性) 如果0
()lim x x f x A →=,且0A >(或0A <),
那么存在常数0δ>,使得当00x x δ<-<时,有()0f x >(或()0f x <). 性质4(函数极限的四则运算法则)如果00()
()
(),(),lim lim x x x x f x A g x B →∞→∞==那么
(1)0()
[()()]lim x x f x g x A B →∞±=±;
(2)0()
[()()]lim x x f x g x A B →∞?=?;
(3)若又有0B ≠,则
0()
()()lim
x x f x A
g x B
→∞=. 例17下列陈述中哪些是对的, 哪些是错的? 如果是对的, 说明理由;如果是错的, 试给出一个反例。
(1)如果0
()lim x x f x →存在, 但0
()lim x x g x →不存在, 那么0
[()()]lim x x f x g x →+不存在;
(2)如果0
()lim x x f x →和0
()lim x x g x →都不存在, 那么0
[()()]lim x x f x g x →+不存在;
(3)如果0
()lim x x f x →存在, 但0
()lim x x g x →不存在, 那么0
()()lim x x f x g x →?不存在.
解: (1)对, 因为, 假若
[()()]
lim x x f x g x →+存在, 则
()[()()]()lim lim lim x x x x x x g x g x f x f x →→→=+-也存在, 这与已知条件矛盾。
(2)错, 例如1,01,0()0,0,()0,01,01,0x x f x x g x x x x >->????
====????-<
当0x →时的极限都不
存在, 但()()0f x g x +≡当0x →时的极限存在。
(3)错, 例如001,0
()0,()0,()0,0,()1,0
lim lim x x x f x f x g x x g x x →→->??
≡===??
不存在,
但0
()()0lim x x f x g x →?=.
例18(函数极限的局部保号性) (1)如果0
()lim x x f x A →=,且0A >(或0A <),
那么存在常数0δ>,使得当00x x δ<-<时,有()0f x >(或()0f x <); (2)如果()lim x f x A →∞
=且0A >(或0A <), 那么存在常数0X >使得当x X
>时有()0f x >(或()0f x <).
注: 例18是一些非常适用的结论, 它们经常可以帮助我们确定方程在给定区间上实根的个数。 方法二 利用一些常用的结论
(1) 有界函数与无穷小的乘积是无穷小。 (2) 当000,0,a b m ≠≠和n 为非负整数时, 有
01
011
01,......0,......,lim m m m n n x n a n m b a x a x a n m b x b x b n m --→∞?=???+++?
>=?+++?
??
?∞
例19 sin lim x x
x →∞
=0. 注:
sin 0lim x x x →∞=, 但0
sin 1lim x x x →=, 我们强烈建议考研学子在计算函数极限时务必要仔细地观察自变量的变化过程, 稍有不慎就会出现重大差错。
练习题: (1)20
1
sin lim x x x
→=________.
(2)arctan lim
x x
x
→∞
=________. 例20 323
2
341751
lim x x x x x →∞++=++3
7. 练习题: (1) 232321
21lim x x x x x →∞-+=-+________.
(2) 322
21
461lim x x x x x →∞-+=-+________. (3) 22
1
21
lim x x x x →∞-=--________. 方法三 利用左、右极限
由于0
00()()()lim lim lim x x x x x x f x A f x f x A +
-
→→→=?==, 鉴于此, 如果我们要考查
函数()f x 当0x x →时极限是否存在, 我们可以去考查函数()f x 在0x 处
的左、右极限是否存在并相等。
适用题型:多用于判别一个分段函数()f x 在分段点0x 处的极限是否存在。
例21 (1992, 3分) 当1x →时, 函数1
2111
x x e x ---的极限 ( D ) (A)等于2. (B)等于0. (C)为∞. (D)不存在但不为∞. 解: 由于
111
1
221111111111(1)0,(1)11lim lim lim lim x x x x x x x x x x e x e e x e x x --++
----→→→→--=+==+=+∞-- 则当1x →时, 函数1
2111
x x e x ---的极限不存在但不为∞. 注: 这里特别应注意的是1100,0lim lim x x
x x e e +
-
→→=+∞=.
练习题: (1) (2000, 5分) 求140
2sin [
]1lim x
x x
e x
x
e
→++
+. (2)设21sin ,0
(),0
x x f x x x x ?>?=?
?≤?, 求0()lim x f x →. (3) 设1ln(1),0(),0
x x x f x e x +≥??
=??
方法四 利用两个重要极限:1(1)lim x
x e x →∞
+=(或者1
0(1)lim x x x e →+=) ,
sin 1lim x x
x →= 在处理1∞型极限时, 经常将所求极限“凑”成基本极限1
(1)lim x x x
→∞
+的
形式, 然后求出极限。
注: 洛必达法则也是一种常用的处理1∞型极限的方法, 但鉴于它的重要性, 我们将在第二部分(一元函数微分学)做专门的总结。 例22 (1991, 5分)
求0lim x x π
+
→.
解
:
2
)[1lim lim x x x e
π
π
+
+
-
→→=+=.
例23 (2011, 10分) 求极限1
1
ln(1)[]lim x e x x x -→+. 解:
1ln(1)1
[1]11
ln(1)11110
00
ln(1)ln(1)ln(1)[
][11][11]lim lim lim x
x x
x x x e e e x
x x x x x x x x x +?-?+----→→→+++=+-=+-
而2
ln(1)1
ln(1)ln(1)1
[1]21
(1)
lim lim lim x x x x x x x x x x
x e x e x →→→++-+--?=
=
=-
-?-
故1
11
20
ln(1)[]lim x e x x e x --→+=. 练习题: (1) (1990, 3分) 设a 是非零常数, 则lim(
)x
x x a x a
→∞
+=-________. (2) (1993, 5分) 求极限2
1lim(sin cos )x x x
x
→∞+. (3) (1995, 3分)
2sin 0
(13)
lim x
x x →+=________.
(4) (1996, 3分) 设2lim(
)8x
x x a x a
→∞+=-, 则a =________. (5) (2003, 4分)
2
1
ln(1)
(cos )lim x x x +→=________. (6) 求极限2
(2sin )lim x x
x x e →+.
(7) 求极限1
1cos
sin ()lim x x x x -→.
(8) 求极限1
1
(1)[]lim x
x x x e →+. (9) 求极限2
(arctan )lim x x x π
→+∞
.
(10) 求极限1
(
)(0,0,0)3lim x x x x x a b c a b c →++>>>. (11) 求极限tan 2
(sin )lim x x x π
→
.
(12) 求极限1
11
lim x
x x
-→.
(13) 求极限1
23lim(
)21
x x x x +→∞
++. 方法五 利用等价无穷小代换
在处理函数极限的过程中, 如果我们能恰当地利用等价无穷小代换, 可以使计算简化。为了便于考研学子复习, 我们把常用的等价无穷小代换列举如下:
当0x →时
, 2sin ~,arcsin ~,tan ~,arctan ~111cos ~1~2ln(1)~,1~x x x x x x x x x
x x x
n
x x e x
-+-
例24 (1994, 3分) 设2
tan (1cos )2ln(12)(1)
lim
x x a x b x c x d e -→+-=-+-, 其中220a c +≠, 则必
有( D )
(A) 4b d = (B) 4b d =- (C) 4a c = (D) 4a c =-
解: 22
00tan 1cos tan (1cos )22ln(12)(1)ln(12)1lim lim x x x x x x
a
b
a x
b x a x x
c c x
d e
x e c d
x x
--→→-++-===--+---+, 从而
4a c =-.
例25 (2008, 9分) 求极限4
[sin sin(sin )]sin lim
x x x x
x
→-. 解:
444
000
[sin sin(sin )]sin [sin sin(sin )]sin (sin )(sin )lim lim lim x x t x x x x x x t t t
x x t →→→---== 32
00
sin 1cos 1
36lim lim t t t t t t t →→--==. 练习题: (1) (1991, 3分) 已知当0x →时, 1
23
(1)1ax +-与cos 1x -是等价无穷小, 则常数a =_______. (2) (1992, 5分)
求0
x x →.
(3) (1993, 3分) 设sin 2
3
40
()sin ,()x
f x t dt
g x x
x =
=+?, 则当0x →时,
()f x 是()g x 的( )
(A)等价无穷小 (B)同阶但非等价的无穷小
(C)高价无穷小 (D)低价无穷小
(4) (1994, 3分) 0
11
limcot (
)sin x x x x
→-=_________. (5) (1997, 3分) 201
3sin cos
(1cos )ln(1)
lim
x x x x x x →+=++__________. (6) (1999, 3分) 2011lim(
)tan x x x x
→-=________. (7) (2004, 4
分) 把0x +→时的无穷小
量
2
2
30
cos ,,x
x t dt t dt αβγ===
??排列起来, 使排在后面的是前一个的高阶无穷小, 则正确的排列次序是( ) (A) ,,αβγ (B) ,,αγβ (C) ,,βαγ (D) ,,βγα
(8) (2006, 3分)
0ln(1)
1cos lim x x x x
→+=-_________. (9) (2007, 4分) 当0x +→时,
等价的无穷小量是( )
(A) 1-
(B)
(C) 1
(D) 1-(10) (2009, 4分) 当0x →时, ()sin f x x ax =-与2()ln(1)g x x bx =- 是等价无穷小, 则( )
(A)
1
1,6a b ==-
(B)
11,6
a b ==
(C)
1
1,6
a b =-=-
(D) 1
1,6
a b =-=
(11)
求极限0lim x +
→.
(12) 20
sin lim
(1)
x
x x x
x e →-=-________. (13) 求极限3
tan sin (sin )lim
x x x
x →-.
(14)
求极限0
x →.
(15) 求极限0
11
lim[
]ln(1)x x x
→-+. 方法六 利用Heine 定理
Heine 定理被经常用于证明某个函数极限的不存在性。为了证明函数
()f x 当0x x →时极限不存在, 我们计划构造两个点列{}{},n n x y 满足如
下条件:
(1) 0lim n n x x →∞=且0()n x x n N +≠?∈; (2) 0lim n n y x →∞
=且0()n y x n N +≠?∈;
(3) lim ()lim ()n n n n f x f y →∞→∞
≠.
从而我们可以说明函数()f x 当0x x →时极限不存在。 例26 证明01limsin x x
→不存在。 证明: 我们特殊地取11
,()22
n n x y n N n n πππ+=
=?∈+, 则显然有
lim 0,0()n n n x x n N +→∞
=≠?∈与lim 0,0()n n n y y n N +→∞
=≠?∈.但由于1
lim sin
0n n
x →∞
=而 1lim sin
1n n y →∞
=, 故01
limsin x x
→不存在。
练习题: 证明0
1
limcos x x
→不存在。 四、 讨论函数连续性,并判断间断点类型
例27 讨论函数221()1lim n
n
n x f x x x →∞
-=+的连续性, 若有间断点, 判别其类型。
解: 由例8知,1()0,1,1
x x f x x x x ?
==??
->?, 从而1x =和1x =-均为()f x 的第一类间
断点。
例28 设函数,0
(),0
x e x f x a x x ?<=?+≥?, 应当怎样选择数a , 使得()f x 成为在
(,)-∞+∞内的连续函数。
解: 要使()f x 成为在(,)-∞+∞内的连续函数, 我们只需
00
lim ()lim ()(0)x x f x f x f a +
-
→→===, 故1a =. 练习题: (1)求函数322
33()6
x x x f x x x +--=+-的连续区间。 (2)设函数()f x 与()g x 在点0x 连续, 证明函数
《高等数学》(同济六版)基础复习教材基础练习题范围完整版(数学二) 2015-03-17 文都-汤家凤 第一章函数与极限 习题1—5(P49) 1(1)~((14) 习题1—6(P56) 1(1)~(6)、2(1)~(4)、4(1)~(5) 习题1—7(P59) 4(1)~(4) 习题1—8(P64) 3(1)~(4)、4 习题1—9(P69) 3(1)~(7)、4(1)~(6) 习题1—10(P74) 1、2、3、5 总习题一(P74) 2、3(1)(2)、9(1)~(6)、10、11、12、13。 第二章导数与微分 习题2—1 5、6、7、8、9(1)~(6)、11、13、14、15、16、17、18、19、20 习题2—2 2(1)~(10)、3(1)~(3)、5、6(1)~(10)、7(1)~(10)、8(1)~(10)、10(1)~(2)、11(1)~(10)、13、14 习题2—3 1(1)~(12)、3(1)~(2)、4、10(1)~(2) 习题2—4 1(1)~(4)、2、3(1)~(4)、4(1)~(4)、5(1)~(2)、6、7(1)~(2)、8(1)~(4) 习题2—5 2、3(1)~(10)、4(1)~(8) 总习题二 1、2、3、6、7、8(1)~(5)、9(1)~(2)、11、12(1)~(2)、13、14。 第三章微分中值定理与导数的应用 习题3—1 1、2、3、4、5、6、7、8、9、10、11、12、13、14 习题3—2 1(1)~(16)、2 习题3—3 1、3、4、5、7、10(1)~(3) 习题3—4 1、2、3(1)~(7)、5(1)~(5)、6、8(1)~(4)、9(1)~(6)、10(1)~(3)、12、13、14 习题3—5 1(1)~(10)、2、4(1)~(3)、8、9、10、16
高等数学教案 一、课程的性质与任务 高等数学是计算机科学与技术;信息管理与信息系统两个专业的一门重要的基础理论课,通过本课程的学习,也是该专业的核心课程。要使学生获得“向量代数”与“空间解析几何”,“微积分”,“常微分方程与无穷级数”等方面的基本概论、基本理论与基本运算;同时要通过各个教学环节逐步培训学生的抽象概括能力、逻辑推理能力、空间想象能力和自学能力。在传授知识的同时,要着眼于提高学生的数学素质,培养学生用数学的方法去解决实际问题的意识、兴趣和能力。 第一章:函数与极限 教学目的与要求18学时 1.解函数的概念,掌握函数的表示方法,并会建立简单应用问题中的函数关系式。 2.解函数的奇偶性、单调性、周期性和有界性。 3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。 4.掌握基本初等函数的性质及其图形。 5.理解极限的概念,理解函数左极限与右极限的概念,以及极限存在与左、右极限之间的关系。 6.掌握极限的性质及四则运算法则。 7.了解极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法。 8.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限。 9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。 10.了解连续函数的性质和初等函数的连续性,了解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质。 第一节:映射与函数 一、集合 1、集合概念 word
word 具有某种特定性质的事物的总体叫做集合。组成这个集合的事物称为该集合的元素 表示方法:用A ,B ,C ,D 表示集合;用a ,b ,c ,d 表示集合中的元素 1)},,,{321 a a a A = 2)}{P x x A 的性质= 元素与集合的关系:A a ? A a ∈ 一个集合,若它只含有有限个元素,则称为有限集;不是有限集的集合称为无限集。 常见的数集:N ,Z ,Q ,R ,N + 元素与集合的关系: A 、B 是两个集合,如果集合A 的元素都是集合B 的元素,则称A 是B 的子集,记作B A ?。 如果集合A 与集合B 互为子集,则称A 与B 相等,记作B A = 若作B A ?且B A ≠则称A 是B 的真子集。 空集φ: A ?φ 2、 集合的运算 并集B A ? :}A x |{x B A B x ∈∈=?或 交集B A ? :}A x |{x B A B x ∈∈=?且 差集 B A \:}|{\B x A x x B A ?∈=且 全集I 、E 补集C A : 集合的并、交、余运算满足下列法则:
高等数学公式 导数公式: 基本积分表: 三角函数的有理式积分: 2 22212211cos 12sin u du dx x tg u u u x u u x += =+-=+=, , , a x x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22 = '='?-='?='-='='2 2 22 11 )(11 )(11 )(arccos 11 )(arcsin x arcctgx x arctgx x x x x +- ='+= '-- ='-= '? ?????????+±+=±+=+=+=+-=?+=?+-==+==C a x x a x dx C shx chxdx C chx shxdx C a a dx a C x ctgxdx x C x dx tgx x C ctgx xdx x dx C tgx xdx x dx x x )ln(ln csc csc sec sec csc sin sec cos 222 22 22 2C a x x a dx C x a x a a x a dx C a x a x a a x dx C a x arctg a x a dx C ctgx x xdx C tgx x xdx C x ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=????????arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 2 2222222? ????++-=-+-+--=-+++++=+-= ==-C a x a x a x dx x a C a x x a a x x dx a x C a x x a a x x dx a x I n n xdx xdx I n n n n arcsin 22ln 22)ln(221 cos sin 22 2222222 2222222 22 2 22 2 π π
《高等数学A》课程教学大纲 (216学时,12学分) 一、课程的性质、目的和任务 高等数学A是理科(非数学)本科个专业学生的一门必修的重要基础理论课,它是为培养我国社会主义现代化建设所需要的高质量专门人才服务的。 通过本课程的学习,要使学生获得:1、函数与极限;2、一元函数微积分学;3、向量代数与空间解析几何;4、多元函数微积分学; 5、无穷级数(包括傅立叶级数); 6、微分方程等方面的基本概念、基本理论和基本运算技能,为学习后继课程和进一步获取数学知识奠定必要的数学基础。 在传授知识的同时,要通过各个教学环节逐步培养学生具有抽象思维能力、逻辑推理能力、空间想象能力、运算能力和自学能力,还要特别注意培养学生具有综合运用所学知识去分析问题和解决问题 的能力。 二、总学时与学分 本课程的安排三学期授课,分为高等数学A(一)、(二)、(三),总学时为90+72+54,学分为5+4+3。 三、课程教学基本要求及基本内容 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了解”、“会”等词表述。 高等数学A(一) 一、函数、极限、连续、 1. 理解函数的概念及函数奇偶性、单调性、周期性、有界性。 2. 理解复合函数和反函数的概念。 3. 熟悉基本初等函数的性质及其图形。 4. 会建立简单实际问题中的函数关系式。 5. 理解极限的概念,掌握极限四则运算法则及换元法则。 6. 理解子数列的概念,掌握数列的极限与其子数列的极限之间的 关系。
7. 理解极限存在的夹逼准则,了解实数域的完备性(确界原理、单界有界数列必有极限的原理,柯西(Cauchy),审敛原理、区间套定理、致密性定理)。会用两个重要极限求极限。 8. 理解无穷小、无穷大、以及无穷小的阶的概念。会用等价无穷 小求极限。 9. 理解函数在一点连续和在一个区间上连续的概念,了解间断点 的概念,并会判别间断点的类型。 10. 了解初等函数的连续性和闭区间上连续函数的性质(介值定理,最大最小值定理,一致连续性)。 二、一元函数微分学 1.理解导数和微分的概念,理解导数的几何意义及函数的可导性与连续性之间的关系。会用导数描述一些物理量。 2.掌握导数的四则运算法则和复合函数的求导法,掌握基本初等函数、双曲函数的导数公式。了解微分的四则运算法则和一阶微分形式不变性。 3.了解高阶导数的概念。 4.掌握初等函数一阶、二阶导数的求法。 5.会求隐函数和参数式所确定的函数的一阶、二阶导数。会求反函数的导数。 6.理解罗尔(Rolle)定理和拉格朗日(Lagrange)定理,了解柯西(Cauchy)定理和泰勒(Taylor)定理。 7.会用洛必达(L’Hospital)法则求不定式的极限。 8.理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法。会求解较简单的最大值和最小值的应用问题。 9.会用导数判断函数图形的凹凸性,会求拐点,会描绘函数的图形(包括水平和铅直渐进线)。 10.了解有向弧与弧微分的概念。了解曲率和曲率半径的概念并会计算曲率和曲率半径。 11.了解求方程近似解的二分法和切线法。 三、一元函数积分学 1. 理解原函数与不定积分的概念及性质,掌握不定积分的基本公式、换元法和分步积分法。会求简单的有理函数及三角函数有理式的积分。 2. 理解定积分的概念及性质,了解函数可积的充分必要条件。
高等数学简明二阶微分方程讲义 作者:齐睿添 ————微分方程的理论帮助了很多工程学,物理学中实际 问题的解决 讨论0. 欧拉公式 欧拉公式在二阶线性齐次常系数方程通解的推导和其非齐次方程的自由项为三角函数时的求解过程中有重要的应用. 讨论1. 二阶常系数线性齐次微分方程 实际问题1. 如图,在水平光滑平面上有一物体在弹簧和阻尼器的牵拉下往复运动.阻力f的大小与物体运动速率成正比,阻力f的方向与速度方向相反(f=-cv).
物体的位置随时间如何变化? 设位置函数x=x(t) 已知: F弹=-kx,f=-cv 故由牛顿第二定律: 合力=-kx-cv=ma 即a+(c/m)v+(k/m)x=0 得到微分方程: 记 得到形如下式的方程(*) 这便是一个二阶常系数线性齐次微分方程. 其通解如下表所示: 特征方程
(上表的具体推导与证明详见教材P174-177) 可以发现其通解形式是符合物块运动的直观直觉的. 1)如果阻力很大,弹簧弹性弱,那么物块晃动两下很快就会停止. 这种情况下,列出方程的通解应是表中第一条或者第二条. 例如:取m=1kg, k=3, c=4, 一开始物块位置在+0.5m处, 给予它一个初速度-5 m/s. 我们依照数学习惯将时间(自变量)记为x, 将位置(因变量)记为y. 那么方程为: . 特征方程为,有两个不相等实根 通解为 把初值条件带入 求得 故该例的解为 图像
2)如果阻力很小,弹簧的弹性很强,那么物块将反复往返震荡,幅度随时间越来越小.这种情况下方程通解应是上表第三条. 例如: 取m=1kg,c=3,k=4,一开始物块位置在+0.5m处, 给予它一个初速度-5 m/s. 即为 带入初值条件 C_1=1/2, C_2=-17根号7/14 图像为
第一章函数与极限 教学目的: 1、理解函数的概念,掌握函数的表示方法,并会建立简单应用问题中的函数关系式。 2、了解函数的奇偶性、单调性、周期性和有界性。 3、理解复合函数及分段函数的概念,了解反函数及隐函数的概念。 4、掌握基本初等函数的性质及其图形。 5、理解极限的概念,理解函数左极限与右极限的概念,以及极限存在与左、右极限 之间的关系。 6、掌握极限的性质及四则运算法则。 7、了解极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限 的方法。 8、理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限。 9、理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。 10、了解连续函数的性质和初等函数的连续性,了解闭区间上连续函数的性质(有 界性、最大值和最小值定理、介值定理),并会应用这些性质。 教学重点: 1、复合函数及分段函数的概念; 2、基本初等函数的性质及其图形; 3、极限的概念极限的性质及四则运算法则; 4、两个重要极限; 5、无穷小及无穷小的比较; 6、函数连续性及初等函数的连续性; 7、区间上连续函数的性质。 教学难点: 1、分段函数的建立与性质; 2、左极限与右极限概念及应用; 3、极限存在的两个准则的应用; 4、间断点及其分类; 5、闭区间上连续函数性质的应用。 §1. 1 映射与函数 一、集合 1. 集合概念 集合(简称集): 集合是指具有某种特定性质的事物的总体. 用A, B, C….等表示. 元素: 组成集合的事物称为集合的元素. a是集合M的元素表示为a?M. 集合的表示: 列举法: 把集合的全体元素一一列举出来. 例如A?{a, b, c, d, e, f, g}. 描述法: 若集合M是由元素具有某种性质P的元素x的全体所组成, 则M可表示为
高等数学公式大全 微分方程的相关概念: 即得齐次方程通解。 , 代替分离变量,积分后将,,,则设的函数,解法:,即写成程可以写成齐次方程:一阶微分方称为隐式通解。 得:的形式,解法: 为:一阶微分方程可以化可分离变量的微分方程 或 一阶微分方程:u x y u u du x dx u dx du u dx du x u dx dy x y u x y y x y x f dx dy C x F y G dx x f dy y g dx x f dy y g dy y x Q dx y x P y x f y -=∴=++====+====+='??)()(),(),()()()()()()(0 ),(),(),(???一阶线性微分方程: ) 1,0()()(2))((0)(,0)() ()(1)()()(≠=+? +?=≠? ===+?--n y x Q y x P dx dy e C dx e x Q y x Q Ce y x Q x Q y x P dx dy n dx x P dx x P dx x P ,、贝努力方程:时,为非齐次方程,当为齐次方程,时当、一阶线性微分方程: 全微分方程: 通解。 应该是该全微分方程的,,其中:分方程,即:中左端是某函数的全微如果C y x u y x Q y u y x P x u dy y x Q dx y x P y x du dy y x Q dx y x P =∴=??=??=+==+),(),(),(0),(),(),(0),(),( 二阶微分方程: 时为非齐次 时为齐次,0)(0)()()()(2 2≠≡=++x f x f x f y x Q dx dy x P dx y d
第一章函数与极限(考研必考章节,其中求极限是本章最重 要的内容,要掌握求极限的集中方法) 第一节映射与函数(一般章节) 一、集合(不用看)二、映射(不用看)三、函数(了解) 注:P1--5 集合部分只需简单了解 P5--7不用看 P7--17 重点看一下函数的四大性态:单调、奇偶、周期、有界 P17--20 不用看 P21 习题1.1 1、2、3大题均不用做 4大题只需做(3)(5)(7)(8) 5--9 均做 10大题只需做(4)(5)(6) 11大题只需做(3)(4)(5) 12大题只需做(2)(4)(6) 13做14不用做15、16重点做 17--20应用题均不用做 第二节数列的极限(一般章节本章用极限定义证的题目考纲不作要求,可不看) 一、数列极限的定义(了解)二、收敛极限的性质(了解) P26--28 例1、2、3均不用证 p28--29 定理1、2、3的证明不用自己证但要会理解 P30 定理4不用看 P30--31 习题1-2 1大题只需做(4)(6)(8) 2--6均不用做 第三节(一般章节)(标题不再写了对应同济六版教材标题) 一、(了解)二、(了解) P33--34 例1、2、3、4、5只需大概了解即可 P35 例6 要会做例7 不用做 P36--37 定理2、3证明不用看定理3’4”完全不用看 p37习题1--3 1--4 均做5--12 均不用做 第四节(重要) 一、无穷小(重要)二、无穷大(了解)
p40 例2不用做 p41 定理2不用证 p42习题1--4 1做 2--5 不全做 6 做 7--8 不用做 第五节(注意运算法则的前提条件是各自存在) p43 定理1、2的证明要理解 p44推论1、2、3的证明不用看 p48 定理6的证明不用看 p49 习题1--5 1题只需做(3)(6)(7)(8)(10)(11)(13)(14) 2、3要做4、5重点做6不做 第六节极限存在准则(重要) 两个重要极限(重要两个重要极限要会证明 p50 准则1的证明要理解 p51 重要极限一定要会独立证明(经典重要极限) p53另一个重要极限的证明可以不用看 p55--56柯西极限存在准则不用看 p56习题1--7 1大题只做(1)(4)(6) 2全做3不用做4全做,其中(2)(3)(5)重点做 第七节(重要) p58--59 定理1、2的证明要理解 p59 习题1--7 全做 第八节(基本必考小题) p60--64 要重点看第八节基本必出考题 p64 习题1--8 1、2、3、4、5要做其中4、5要重点做 6--8不用做
第一部分函数极限连续
历年试题分类统计及考点分布 本部分常见的题型 1.求分段函数的复合函数。 2.求数列极限和函数极限。 3.讨论函数连续性,并判断间断点类型。 4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数 例1 (1988, 5分) 设2 (),[()]1x f x e f x x ?==-且()0x ?≥,求()x ?及其定义域。 解: 由2 ()x f x e =知2 ()[()]1x f x e x ??==-,又()0x ?≥, 则()0x x ?=≤. 例2 (1990, 3分) 设函数1,1 ()0,1 x f x x ?≤?=?>??,则[()]f f x =1. 练习题: (1)设 1,1, ()0,1,(),1,1, x x f x x g x e x ??求[()]f g x 和[()]g f x , 并作出这 两个函数的图形。 (2) 设 20,0,0,0, ()(), ,0,,0, x x f x g x x x x x ≤≤??==??>->??求 [()],[()],[()],[()]f f x g g x f g x g f x . 二、 求数列的极限 方法一 利用收敛数列的常用性质 一般而言,收敛数列有以下四种常用的性质。 性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。 性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。 性质3(收敛数列的保号性) 如果lim n n x a →∞ =,且0a >(或0a <),那么存在 0n N +∈,使得当0n n >时,都有0n x >(或0n x <). 性质4(数列极限的四则运算法则) 如果,,lim lim n n n n x a y b →∞ →∞ ==那么 (1)()lim n n n x y a b →∞ ±=±; (2)lim n n n x y a b →∞ ?=?; (3)当0()n y n N +≠∈且0b ≠时,lim n n n x a y b →∞ =.
目录 一、函数与极限 (2) 1、集合的概念 (2) 2、常量与变量 (3) 2、函数 (4) 3、函数的简单性态 (4) 4、反函数 (5) 5、复合函数 (6) 6、初等函数 (6) 7、双曲函数及反双曲函数 (7) 8、数列的极限 (8) 9、函数的极限 (10) 10、函数极限的运算规则 (11)
一、函数与极限 1、集合的概念 一般地我们把研究对象统称为元素,把一些元素组成的总体叫集合(简称集)。集合具有确定性(给定集合的元素必须是确定的)和互异性(给定集合中的元素是互不相同的)。比如“身材较高的人”不能构成集合,因为它的元素不是确定的。 我们通常用大字拉丁字母A、B、C、……表示集合,用小写拉丁字母a、b、c……表示集合中的元素。如果a是集合A中的元素,就说a属于A,记作:a∈A,否则就说a不属于A,记作:a A。 ⑴、全体非负整数组成的集合叫做非负整数集(或自然数集)。记作N ⑵、所有正整数组成的集合叫做正整数集。记作N+或N+。 ⑶、全体整数组成的集合叫做整数集。记作Z。 ⑷、全体有理数组成的集合叫做有理数集。记作Q。 ⑸、全体实数组成的集合叫做实数集。记作R。 集合的表示方法 ⑵、列举法:把集合的元素一一列举出来,并用“{}”括起来表示集合 ⑵、描述法:用集合所有元素的共同特征来表示集合。 集合间的基本关系 ⑴、子集:一般地,对于两个集合A、B,如果集合A中的任意一个元素都是集合B的元素,我们就说A、B有包含关系,称集合A为集合B的子集,记作A B(或B A)。。 ⑵相等:如何集合A是集合B的子集,且集合B是集合A的子集,此时集合A中的元素与集合B中的元素完全一样,因此集合A与集合B相等,记作A=B。 ⑶、真子集:如何集合A是集合B的子集,但存在一个元素属于B但不属于A,我们称集合A是集合B的真子集。 ⑷、空集:我们把不含任何元素的集合叫做空集。记作,并规定,空集是任何集合的子集。 ⑸、由上述集合之间的基本关系,可以得到下面的结论: ①、任何一个集合是它本身的子集。即A A ②、对于集合A、B、C,如果A是B的子集,B是C的子集,则A是C的子集。 ③、我们可以把相等的集合叫做“等集”,这样的话子集包括“真子集”和“等集”。 集合的基本运算 ⑴、并集:一般地,由所有属于集合A或属于集合B的元素组成的集合称为A与B的并集。记作A ∪B。(在求并集时,它们的公共元素在并集中只能出现一次。) 即A∪B={x|x∈A,或x∈B}。 ⑵、交集:一般地,由所有属于集合A且属于集合B的元素组成的集合称为A与B的交集。记作A ∩B。 即A∩B={x|x∈A,且x∈B}。 ⑶、补集:
学姐偷懒直接从网上下了一份公式总结,然后按照咱们的考试要求改了一下,特别诡异的那些公式我都删掉了,剩下的都是可能会出现的,哪些必须记哪些可以记也都写在后面了,有的出题形式我也加在知识点后面了,可以做个参考。这上面的知识点不很全,但应付考试差不多了,上面没有的学霸们可以自己再看看书哈。重点关注黑体字!!!电子版已发各部长,可以找部长要。祝大家都能考个好成绩~ ——魏亚杰 高等数学(一)上 公式总结 第一章 一元函数的极限与连续 1、一些初等函数公式:(孩子们。没办法,背吧) sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan cot cot 1cot()cot cot αβαβαβ αβαβαβαβ αβαβ αβαββα±=±±=±±= ??±=±和差角公式: sin sin 2sin cos 22 sin sin 2cos sin 22 cos cos 2cos cos 22 cos cos 2sin sin 22 αβ αβ αβαβαβ αβαβαβαβαβαβαβ+-+=+--=+-+=+--=和差化积公式: 1 sin cos [sin()sin()] 21 cos sin [sin()sin()] 21 cos cos [cos()cos()] 21 sin sin [cos()cos()] 2 αβαβαβαβαβαβαβαβαβαβαβαβ=++-=+--=++-=+--积化和差公式: 222222sin 22sin cos cos 22cos 1 12sin cos sin 2tan tan 21tan cot 1 cot 22cot αααααααα α ααααα ==-=-=-= --= 倍角公式:
考研数学辅导书比较,一个比较经典的帖子,重温一下。 1.李永乐考研数学复习全书 题型很全面,内容很充实(线代和概率很不错,微积分稍逊)难度要高于真题,所谓的简单是命题的风格 很常规,没有什么剑走偏锋让人一下傻眼的题,考研真题不正是这样的吗? 做熟练(我不知道怎么叫做透哈)120以上真不难,135以上就要看临场发挥。 --------------------------------------------------------------------------------------------------------------------------------------------------------- 2.陈文灯考研数学复习指南 个别题其实已经很陈旧了,难度也有被夸大的嫌疑。很大一部分也是注重基础的题只是不像全书加以强调 和总结,微积分部分题型归纳很好,个别题有难度(真不多),但有助于锻炼思维。线代和概率内容显单 薄。 PS:无穷级数,积分,不等式证明,泰勒公式,中值定理等是精华,做过思路会很清晰。传说,考高分要 做指南,我想,是因为指南在你有一定基础之后,能对你的思维有一个提炼吧。 --------------------------------------------------------------------------------------------------------------------------------------------------------- 3.蔡燧林考研数学标准全书 微积分部分例题精华,讲解很深入,给人醍醐灌顶的感觉。所谓精华就是不会边边角角都涉及到的意思, 所以还是要做点非精华的练习(比如全书??^_^) 线代一般,概率一般,纸张一般,印刷一般。 ps :章后练习很多,但一定要做,那个也是精华。 --------------------------------------------------------------------------------------------------------------------------------------------------------- 4.水木艾迪微积分通用讲义 配合水木的视频,很好的哈。把解题中的疑难提出来,然后列举例题加以解决分析。章前的知识点讲解也 很好,选题很也典型。总之,比全书微积分要好,值得一读。 PS:多元微分,一元微积分非常好。 --------------------------------------------------------------------------------------------------------------------------------------------------------- 5.赵达夫高等数学辅导讲义 体例不好,一堆知识点,一堆练习,一堆解答。章后练习选题还是很好的,不一定很难,但非常典型。但 PS:只靠这一本书是不够的。是不是叫不给力? --------------------------------------------------------------------------------------------------------------------------------------------------------- 6.黄庆怀高等数学辅导教材 同学们骂我书托吧,我做了这么多书,最想推荐的就是这本了。 体例好,内容全,例题典型,归纳完整,练习题保质保量。唯一稍差是讲解不够(全书和标
微积分初步 一、微积分的基本概念 1、极限 极限指无限趋近于一个固定的数值 两个常见的极限公式 0sin lim 1x x x →= *1lim 11x x x →∞??+= ??? 2、导数 当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限叫做导数。 0'lim x dy y y dx x ?→?==? 导数含义,简单来说就是y 随x 变化的变化率。 导数的几何意义是该点切线的斜率。 3、原函数和导函数 对原函数上每点都求出导数,作为新函数的函数值,这个新的函数就是导函数。 00()()'()lim lim x x y y x x y x y x x x ?→?→?+?-==?? 4、微分和积分 由原函数求导函数:微分 由导函数求原函数:积分 微分和积分互为逆运算。 例1、根据导函数的定义,推导下列函数的导函数 (1)2y x = (2) (0)n y x n =≠ (3)sin y x = 二、微分 1、基本的求导公式 (1)()'0 ()C C =为常数 (2)()1' (0)n n x nx n -=≠ (3)()'x x e e = *(4)()'ln x x a a a = (5)()1ln 'x x = *(6)()1log 'ln a x x a =
(7)()sin 'cos x x = (8)()cos 'sin x x =- (9)()21tan 'cos x x = (10)()21cot 'sin x x = **(11)() arcsin 'x = **(12)()arccos 'x = **(13)()21arctan '1x x =+ **(14)()2 1arccot '1x x =-+ 2、函数四则运算的求导法则 设u =u (x ),v =v (x ) (1)()'''u v u v ±=± (2)()'''uv u v uv =+ (3)2'''u u v uv v v -??= ??? 例2、求y=tan x 的导数 3、复合函数求导 对于函数y =f (x ),可以用复合函数的观点看成y =f [g (x)],即y=f (u ),u =g (x ) 'dy dy du y dx du dx == 即:'''u x y y u = 例3、求28(12)y x =+的导数 例4、求ln tan y x =的导数 三、积分 1、基本的不定积分公式 下列各式中C 为积分常数 (1) ()kdx kx C k =+?为常数 (2)1 (1)1n n x x dx C n n +=+≠-+?
第四章不定积分 教学目的: 1、理解原函数概念、不定积分的概念。 2、掌握不定积分的基本公式,掌握不定积分的性质,掌握换元积分法(第一,第二) 与分部积分法。 3、会求有理函数、三角函数有理式和简单无理函数的积分。 教学重点: 1、不定积分的概念; 2、不定积分的性质及基本公式; 3、换元积分法与分部积分法。 教学难点: 1、换元积分法; 2、分部积分法; 3、三角函数有理式的积分。
§4 1 不定积分的概念与性质 一、教学目的与要求: 1.理解原函数与不定积分的概念及性质。 2.掌握不定积分的基本公式。 二、重点、难点:原函数与不定积分的概念 三、主要外语词汇:At first function ,Be accumulate function , Indefinite integral ,Formulas integrals elementary forms. 四、辅助教学情况:多媒体课件第四版和第五版(修改) 五、参考教材(资料):同济大学《高等数学》第五版
一、原函数与不定积分的概念 定义1 如果在区间I 上, 可导函数F (x )的导函数为f (x ), 即对任一x ∈I , 都有 F '(x )=f (x )或dF (x )=f (x )dx , 那么函数F (x )就称为f (x )(或f (x )dx )在区间I 上的原函数. 例如 因为(sin x )'=cos x , 所以sin x 是cos x 的原函数. 又如当x ∈(1, +∞)时, 因为x x 21)(=', 所以x 是x 21的原函数. 提问: cos x 和x 21还有其它原函数吗? 原函数存在定理 如果函数f (x )在区间I 上连续, 那么在区间I 上存在可导函数F (x ), 使对任一x ∈I 都有 F '(x )=f (x ). 简单地说就是: 连续函数一定有原函数. 两点说明: 第一, 如果函数f (x )在区间I 上有原函数F (x ), 那么f (x )就有无限多个原函数, F (x )+C 都是f (x )的原函数, 其中C 是任意常数. 第二, f (x )的任意两个原函数之间只差一个常数, 即如果Φ(x )和F (x )都是f (x )的原函数, 则 Φ(x )-F (x )=C (C 为某个常数). 定义2 在区间I 上, 函数f (x )的带有任意常数项的原函数称为f (x )(或f (x )dx )在区间I 上的不定积分, 记作 ?dx x f )(. 其中记号?称为积分号, f (x )称为被积函数, f (x )dx 称为被积表达式, x 称为积分变量. 根据定义, 如果F (x )是f (x )在区间I 上的一个原函数, 那么F (x )+C 就是f (x )的不定积分, 即 ?+=C x F dx x f )()(. 因而不定积分dx x f )(?可以表示f (x )的任意一个原函数. 例1. 因为sin x 是cos x 的原函数, 所以 C x xdx +=?sin cos . 因为x 是x 21的原函数, 所以 C x dx x +=?21.
第三章 一元函数积分学 §3.1 不定积分 甲 内容要点 一.基本概念与性质 1.原函数与不定积分的概念 设函数()x f 和()x F 在区间I 上有定义,若()()x f x F ='在区间I 上成立,则称()x F 为()x f 在区间 I 上的原函数,()x f 在区间I 中的全体原函数称为()x f 在区间I 的不定积分,记以()?dx x f 。其中?称 为积分号,x 称为积分变量,()x f 称为被积函数,()dx x f 称为被积表达式。 2.不定积分的性质 设 ()()C x F dx x f +=?,其中()x F 为()x f 的一个原函数,C 为任意常数。 则(1)()()C x F dx x F +='? 或 ()()? +=C x F x dF (2) ()[]()x f dx x f ='? 或 ()[]()dx x f dx x f d =? (3)()()? ? =dx x f k dx x kf (4) ()()[]()()???±=±dx x g dx x f dx x g x f 3.原函数的存在性 设()x f 在区间I 上连续,则()x f 在区间I 上原函数一定存在,但初等函数的原函数不一定是初等函数。例如() ?dx x 2sin ,() ?dx x 2 cos , ?dx x x sin ,?dx x x cos ,?x dx ln ,dx e x ?-2 等。被积函数有原函数, 但不能用初等函数表示,故这些不定积分均称为积不出来。
二.基本积分公式 1.C x dx x ++= ?+1 1 ααα (),实常数1-≠α 2. ?+=C x dx x ln 1 3.?+=C a a dx a x x ln 1 ()1,0≠>a a C e dx e x x +=? 4.? +=C x xdx sin cos 5.? +-=C x xdx cos sin 6.C x dx x xdx +== ??tan cos 1 sec 22 7.C x dx x xdx +-==??cot sin 1csc 2 2 8.C x xdx x +=? sec sec tan 9.C x xdx x +-=? csc csc cot 10.C x xdx +-=? cos ln tan 11.C x xdx +=? sin ln cot 12.C x x xdx ++=? tan sec ln sec 13.C x x xdx +-=? cot csc ln csc 14. ? +=-C a x x a dx arcsin 2 2 ()0>a 15. C a x a x a dx +=+?arctan 122 ()0>a 16. C x a x a a x a dx +-+=-?ln 2122 ()0>a 17. C a x x a x dx +±+=±? 222 2ln () 0>a
《高等数学》教案 第一讲 函数与极限 1.函数的定义 设有两个变量x ,y 。对任意的x ∈D ,存在一定规律f ,使得y 有唯一确定的值与之对应,则y 叫x 的函数。记作y=f(x),x ∈D 。其中x 叫自变量,y 叫因变量。 函数两要素:对应法则、定义域,而函数的值域一般称为派生要素。 例1:设f(x+1)=2x 2+3x-1,求f(x). 解:设x+1=t 得x=t-1,则f(t)=2(t-1)2+3(t-1)-1=2t 2-t-2 ∴f(x)=2x 2 – x – 2 定义域:使函数有意义的自变量的集合。因此,求函数定义域需注意以下几点: ①分母不等于0 ②偶次根式被开方数大于或等于0 ③对数的真数大于0 例2 求函数y= 6—2x -x +arcsin 7 1 2x -的定义域. 解:要使函数有定义,即有: 1|7 12|062≤-≥--x x x ? 4323≤≤--≤≥x x x 或?4323≤≤-≤≤-x x 或 于是,所求函数的定义域是:[-3,-2] [3,4]. 例3 判断以下函数是否是同一函数,为什么? (1)y=lnx 2与y=2lnx (2)ω=u 与y=x 解 (1)中两函数的 定义域不同,因此不是相同的函数. (2)中两函数的 对应法则和定义域均相同,因此是同一函数. 2. 初等函数 (1)基本初等函数 常数函数:y=c(c 为常数) 幂函数: y=μ x (μ为常数) 指数函数:y=x a (a>0,a ≠1,a 为常数) 对数函数:y=x a log (a>0,a ≠1,a 为常数) 三角函数:y=sinx y=cosx y=tanx y=cotx y=secx y=cscx 反三角函数:y=arcsinx y=arccosx y=arctanx y=arccotx (2)复合函数 设),(u f y =其)(x u ?=中,且)(x ?的值全部或部分落在)(u f 的定义域内,则称)]([x f y ?=为x 的复合函数,而u 称为中间变量. 例4:若y=u ,u = sinx ,则其复合而成的函数为y=x sin ,要求u 必须≥0, ∴sinx ≥0,x ∈[2k π,π+2k π] 例5:分析下列复合函数的结构
此文档分为两部分:高等数学公式(13页)和补充的三角函数公式(7页)。 声明:源材料来自网络,自己稍加整理。 第一部分:高等数学公式 导数公式: 基本积分表: a x x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22= '='?-='?='-='='2 2 22 11 )(11 )(11 )(arccos 11 )(arcsin x arcctgx x arctgx x x x x +- ='+= '-- ='-= '? ?????????+±+=±+=+=+=+-=?+=?+-==+==C a x x a x dx C shx chxdx C chx shxdx C a a dx a C x ctgxdx x C x dx tgx x C ctgx xdx x dx C tgx xdx x dx x x )ln(ln csc csc sec sec csc sin sec cos 222 22 22 2C a x x a dx C x a x a a x a dx C a x a x a a x dx C a x arctg a x a dx C ctgx x xdx C tgx x xdx C x ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=????????arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 2 2222222? ????++-=-+-+--=-+++++=+-= ==-C a x a x a x dx x a C a x x a a x x dx a x C a x x a a x x dx a x I n n xdx xdx I n n n n arcsin 22ln 22)ln(221 cos sin 22 2222222 2222222 22 2 22 2 π π
第一部分函数极限连续 函数、极限、 连续 函数极限连续 函数概念函数的四种反函数与复初等函数数列极限函数极限连续概念间断点分类初等函数的连闭区间上连续特征合函数续性函数的性质 函数的有界数列极限的函数极限的第一类间断有界性与最大性定义定义点值最小值定理函数的单调收敛数列的函数极限的可去间断点零点定理性性质性质 函数的奇偶极限的唯一函数极限的跳跃间断点 性性唯一性 函数的周期收敛数列的函数极限的第二类间断 性有界性局部有界性点 收敛数列的函数极限的 保号性局部保号性 数列极限四函数极限与数 则运算法则列极限的关系 极限存在准函数极限四 则则运算法则 夹逼准则两个重要极 限 单调有界准无穷小的比 则较 高阶无穷小 低阶无穷小 同阶无穷小 等价无穷小
历年试题分类统计及考点分布 考点复合函数极限四则两个重要单调有界无穷小的合计 运算法则极限准则阶 年份 1987 1988 5 3 8 1989 1990 3 3 6 1991 5 3 8 1992 3 3 1993 5 3 8 1994 3 3 1995 3 3 1996 3 6 3 12 1997 3 3 1998 1999 2000 5 5 2001 2002 2003 4 4 8 2004 4 4 2005 2006 12 3 15 2007 4 4 2008 4 4 2009 4 4 2010 4 4 2011 10 10 20 合计8 18 37 32 27 本部分常见的题型 1.求分段函数的复合函数。 2.求数列极限和函数极限。 3.讨论函数连续性,并判断间断点类型。 4.确定方程在给定区间上有无实根。