
中考复习专题——切线长定理与弦切角定理
【知识要点】
1.切线长定理:过圆外一点P做该圆的两条切线,切点为A、B。AB交PO于点C,则有如下结论:
(1)PA=PB
(2)PO⊥AB,且PO平分AB
(3)APO BPO OAC OBC
∠=∠=∠=∠;AOP BOP CAP CBP
∠=∠=∠=∠
2.弦切角定理:弦切角(切线与圆的夹角)等于它所夹的弧所对的圆周角
推论:若两弦切角所夹的弧相等,则这两个弦切角也相等
【典型例题】
【例1】如图1,AB,AC是⊙O的两条切线,切点分别为B、C、D是优弧
?BC上的点,已知∠BAC=800,那么∠BDC =______.
图1 图2 图3
举一反三:
1.如图2,AB是⊙O的弦,AD是⊙O的切线,C为
?AB上任一点,∠ACB=1080,那么∠BAD =______.
2.如图3,PA,PB切⊙O于A,B两点,AC⊥PB,且与⊙O相交于D,若∠DBC=220,则∠APB=________.
【例2】如图,已知圆上的弧??
AC BD
=,过C点的圆的切线与BA的延长线交于E点,证明:
(1)∠ACE=∠BCD;
(2)BC2=BE×CD .
C
B
O
A
D
A
D
P
O
举一反三:
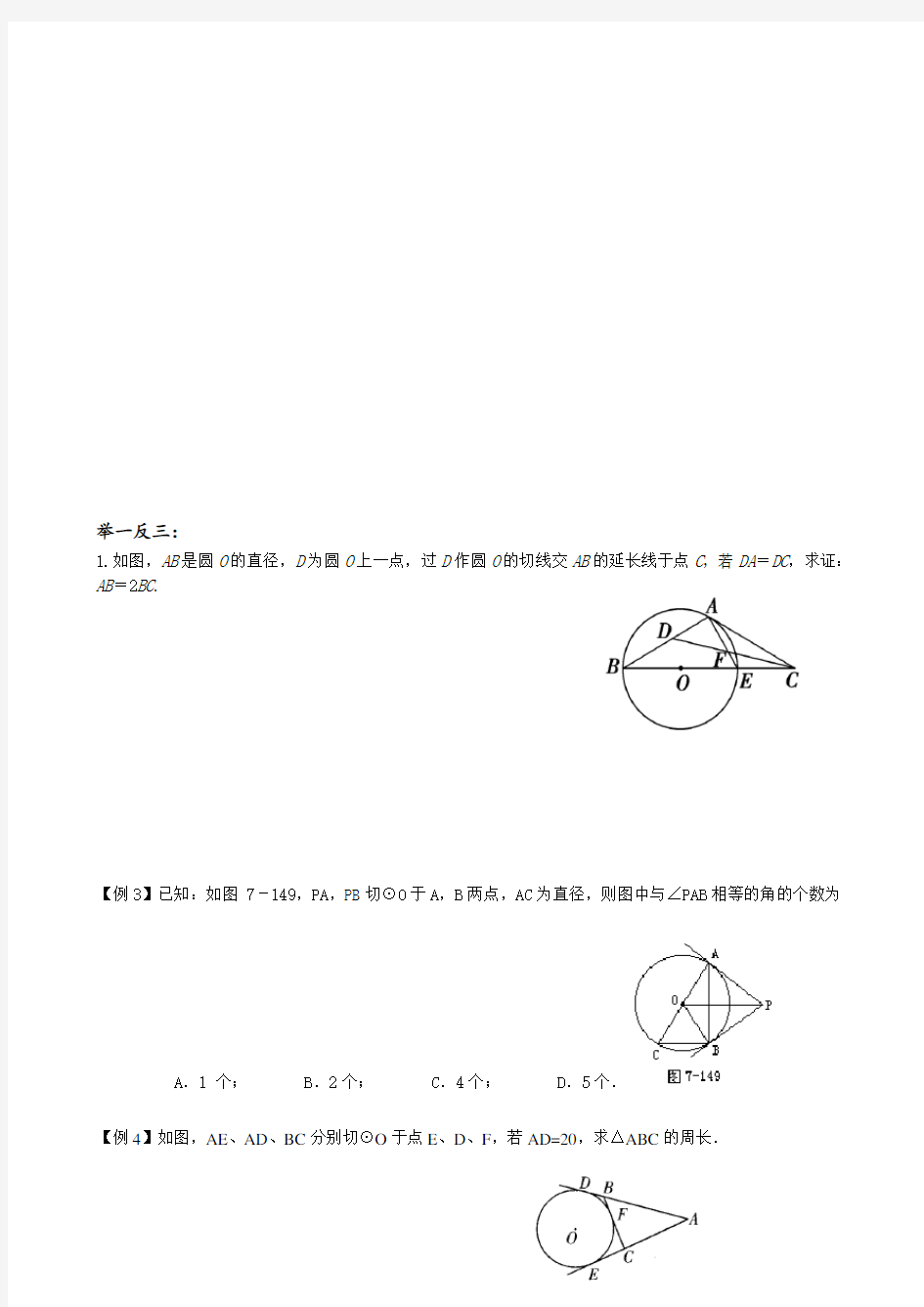
1.如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB的延长线于点C,若DA=DC,求证:AB=2BC.
【例3】已知:如图 7-149,PA,PB切⊙O于A,B两点,AC为直径,则图中与∠PAB相等的角的个数为
A.1 个;B.2个;C.4个;D.5个.
【例4】如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
P
B
A
O
举一反三:
1. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.
(1)求∠APB 的度数;
(2)当OA =3时,求AP 的长.
2.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的长.
3.已知:如图,△ABC 三边BC =a ,CA =b ,AB =c ,它的内切圆O 的半径长为r .求△ABC 的面积S .
4. 如图,在△ABC 中,已知∠ABC=90o ,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.
【课后作业】
1.如图1,CD 是⊙O 的直径,AE 切⊙O 于点B ,连接DB ,若20D ∠=?,则DBE ∠的大小为( )
A. 20?
B. 40?
C. 60?
D. 70?
图1 图2 图3
2.如图2,ABC ?是圆的内接三角形,PA 切圆于点A ,PB 交圆于点D .若60ABC ∠=o
,1PD =,
8BD =,则PAC ∠=________,PA =________.
3.如图3,AB 是半圆O 的直径,C 、D 是半圆上的两点,半圆O 的切线PC 交AB 的延长线于点P , ∠PCB =25°,则∠ADC 为
A.105°
B.115°
C.120°
D.125°
4.如图4,AB 是⊙O 的直径,EF 切⊙O 于C ,AD ⊥EF 于D ,AD=2,AB=6,则AC 的长为 A.2 B.3 C.23
图4 图5 图6
5.如图5,AB 是⊙ O 的直径,AC 、BC 是⊙ O 的弦,PC 是⊙ O 的切线,切点为 C ,∠BAC=350
,那么∠ACP 等于
A. 350
B. 550
C. 650
D. 1250
C
D
E O
A
F
B
O A
B
D E
O A C
B D
A P
C O
D B C
D
6.如图6,在⊙ O中,AB是弦,AC是⊙ O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙ O于 E点,若 AE平分∠BAD,则∠BAD=
A. 300
B. 450
C. 500
D. 600
7.已知:如图7-154,⊙O的半径OA⊥OB,过A点的直线交OB于P,交⊙O于Q,过Q引⊙O的切线交OB延长线于C,且PQ=QC.求∠A的度数.
8.已知:如图7-155,⊙O内接四边形ABCD,MN切⊙O于C,∠BCM=38°,AB为⊙O直径.求∠ADC的度数.
9.已知:如图,圆内接四边形ABCD的AB边经过圆心,AD,BC的延长线相交于E,过C点的切线CF ⊥AE于F.求证:
(1)△ABE为等腰三角形;
(2)若 BC=1cm,AB=3cm,求EF的长.
几何表示 过三角形外接圆上异于三角形顶点的任意一点作三边的垂线, 则三垂足共线. □ 一阶描述 基本定义: 选定 A,B,C 三点 □ 取外接圆上任意一点 P □ 得到三个垂足 D,E,F □ 基本描述: : A,B,C 三点不共线 西姆松定理 它们的坐标分别为 这三点构成的三角形的外接圆心及半径分别为 P 点的坐标为 . 全部 (x 1,y 1),(x 2,y 2),(x 3,y 3).l 1=AB,l 2=BC,l 3=CA.(u,v),r.(a,b)D(a 1,b 1),E(a 2,b 2),F(a 3,b 3). 91
□ ● : P 在三角形 ABC 的外接圆上 □ ● : P 不同于 A,B,C □ ● : D 是 P 到 BC 的垂足 □ ● : E 是 P 到 CA 的垂足 □ l 1l 2l 3(l 21=(x 1-x 2)2+(y 1-y 2 )2 [l 22=(x 2-x 3)2+(y 2-y 3)2 [l 23=(x 3-x 1)2+(y 3-y 1 )2[l 1+l 2>l 3[l 2+l 3>l 1[l 3+l 1> l 2)92^uvr ((x 1-u)2 +(y 1-v)2=r 2 [ (x 2-u)2+(y 2-v)2=r 2[(x 3-u)2 +(y 3-v)2 =r 2 [(u-a)2+(v-b)2=r 2) 93\(a=x 1[b=y 1)[\(a=x 2[b=y 2)[\(a=x 3[b=y 3) 94(a 1-x 2)(b 1-y 3)-(a 1-x 3)(b 1-y 2)=0[(a 1-a)(x 2-x 3)+(b 2-b)(y 2-y 3)=0 95^
切线长定理弦切角定理切割线定理相交弦定理 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
切线长定理、弦切角定理、切割线定理、相交弦定理 以及与圆有关的比例线段 [学习目标] 1.切线长概念 切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直 线,它不可以度量长度。 2.切线长定理 对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相 等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆 外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆 外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5) 圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。 直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢(四个) 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。 5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。 6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定 理。 7.与圆有关的比例线段 定理图形已知结论证法 相交弦 定理 ⊙O中,AB、CD为 弦,交于P. PA·PB= PC·PD. 连结AC、BD,证: △APC∽△DPB.
相交弦定理的推论⊙O中,AB为直 径,CD⊥AB于P. PC2=PA·PB.用相交弦定理. 切割线定理⊙O中,PT切⊙O于 T,割线PB交⊙O于 A PT2=PA·PB连结TA、TB,证: △PTB∽△PAT 切割线定理推论PB、PD为⊙O的两 条割线,交⊙O于 A、C PA·PB= PC·PD 过P作PT切⊙O于 T,用两次切割线定 理 圆幂定理⊙O中,割线PB交 ⊙O于A,CD为弦 P'C·P'D=r2- OP'2 PA·PB=OP2- r2 r为⊙O的半径 延长P'O交⊙O于 M,延长OP'交⊙O 于N,用相交弦定理 证;过P作切线用 切割线定理勾股定 理证 8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。 【典型例题】 例1.如图1,正方形ABCD的边长为1,以BC为直径。在正方形内作半圆O,过A作半圆切线,切点为F,交CD于E,求DE:AE的值。 图1 解:由切线长定理知:AF=AB=1,EF=CE 设CE为x,在Rt△ADE中,由勾股定理
弦切角定理及其推论 定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。 弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. 证明:设圆心为O,连接OC,OB,。 ∵∠TCB=90°-∠OCB ∵∠BOC=180°-2∠OCB ∴∠BOC=2∠TCB (定理:弦切角的度数等于它所夹的弧所对的圆心角的度数的一半)∵∠BOC=2∠CAB(同一弧所对的圆心角等于圆周角的两倍) ∴∠TCB=∠CAB (定理:弦切角的度数等于它所夹的弧的圆周角) 弦切角定理推论:两弦切角所夹的弧相等,则这两个弦切角也相等。 应用举例:
第一个算出地球周长的人 ──埃拉托色尼 2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的埃拉托色尼。 埃拉托色尼博学多才,他不仅通晓天文,而且熟知地理;又是诗人、历史学家、语言学家、哲学家,曾担任过亚历山大博物馆的馆长。 细心的埃拉托色尼发现:离亚历山大城约800公里的塞恩城(今埃及阿斯旺附近),夏日正午的阳光可以一直照到井底,因而这时候所有地面上的直立物都应该没有影子。但是,亚历山大城地面上的直立物却有一段很短的影子。他认为:直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。从地球是圆球和阳光直线传播这两个前提出发,从假想的地心向塞恩城和亚历山大城引两条直线,其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。按照相似三角形的比例关系,已知两地之间的距离,便能测出地球的圆周长。埃拉托色尼测出夹角约为7度,是地球圆周角(360度)的五十分之一,由此推算地球的周长大约为4万公里,这与实际地球周长(40076公里)相差无几。他还算出太阳与地球间距离为1.47亿公里,和实际距离1.49亿公里也惊人地相近。这充分反映了埃拉托色尼的学说和智慧。 埃拉托色尼是首先使用“地理学”名称的人,从此代替传统的“地方志”,写成了三卷专著。书中描述了地球的形状、大小和海陆分布。埃拉托色尼还用经纬网绘制地图,最早把物理学的原理与数学方法相结合,创立了数理地理学。
切线长定理典型练习题 一、填空题 1、如图AB 为⊙O 的直径,CA 切⊙O 于点A ,CD=1cm ,DB=3cm ,则AB=______cm 。 2、已知三角形的三边分别为 3、 4、5,则这个三角形的内切圆半径是 。 3、三角形的周长是12,面积是18,那么这个三角形的内切圆半径是 。 二、选择题 1、△ABC 内接于圆O ,AD ⊥BC 于D 交⊙O 于E ,若BD=8cm , CD=4cm ,DE=2cm ,则△ABC 的面积等于( ) A.248cm B.296cm C.2108cm D.232cm 2、正方形的外接圆与内切圆的周长比为( ) A. 1:2 B. 2:1 C. 4:1 D. 3:1 3、在三角形内,与三角形三条边距离相等的点,是这个三角形的 ( ) A.三条中线的交点, B.三条角平分线的交点, C.三条高的交点, D.三边的垂直平分线的交点。 4、△ABC 中,内切圆I 和边BC 、CA 、AB 分别相切于点D 、E 、F ,则∠FDE 与∠A 的关系 是 ( ) A. ∠FDE=21∠A B . ∠FDE+21∠A=180° C . ∠FDE+2 1∠A=90° D . 无法确定 三、解答题: 1、如图,AB 、CD 分别与半圆O 切于点A 、D ,BC 切⊙O 于点E ,若AB =4,CD =9,求⊙O 的半径。 2、等腰三角形的腰长为13cm ,底边长为10 cm ,求它的内切圆的半径。 3、如图,在△ABC 中,∠C=90°,以BC 上一点O 为圆心,以OB 为半径的圆交AB 于点M ,交BC 于点N 。 (1)求证:B A ·BM=BC ·BN ; (2)如果CM 是⊙O 的切线,N 为OC 的中点。当AC=3时,求AB 的值。
C B O A D C E O A B D 弦切角定理测试卷 姓名 _____ 1.已知一个圆的弦切角等于50°,那么这个弦切角所夹的弧所对的圆心角的度数为 _______ . 2.如图,AB 是直径,点D 在AB 的延长线上,BD=OB ,若CD 切⊙O 于C 点,则∠CAB 的度数为 ,∠DCB 的度数为 ,∠ECA 的度数为 ___ . 3.如图,AB , AC 是⊙O 的两条切线,切点分别为 B 、 C 、 D 是优弧BC 上的点,已知 ∠BAC=800,那么∠BDC =______. 4.如图,AB 是⊙ O 的弦, AD 是⊙ O 的切线,C 为弧AB 上任一点,∠ACB=1080,那么∠BAD =______. 5.如图,PA , PB 切⊙ O 于 A , B 两点, AC ⊥PB ,且与⊙ O 相交于 D ,若∠DBC=220,则∠APB==________. 2题图 3题图 4题图 5 题图 6、如图,CD 是⊙O 的直径,AE 切⊙O 于点B ,连接DB ,若20D ? ,则DBE D的大小为( ) A. 20° B. 40° C. 60° D. 70° 7、如图,AB 是半圆O 的直径,C 、D 是半圆上的两点,半圆O 的切线PC 交AB 的延长线于点P ,∠PCB =25°,则∠ADC 为( ) A.105° B.115° C.120° D.125° 8、如图,AB 是⊙O 的直径,EF 切⊙O 于C ,AD ⊥EF 于D ,AD=2,AB=6,则AC 的长为( ) A.2 B.3 C.23 D.4 9、如图,AB 是⊙ O 的直径, AC , BC 是⊙ O 的弦, PC 是⊙ O 的切线,切点为 C ,∠BAC=350 ,那么∠ACP 等于( )A. 350 B. 550 C. 650 D. 125 6题图 7题图 8题图 9题图 10、如图,在⊙ O 中, AB 是弦, AC 是⊙ O 的切线, A 是切点,过 B 作BD ⊥AC 于D ,BD 交⊙ O 于 E 点,若 AE 平分∠BAD ,则∠BAD=( ) A. 300 B. 450 C. 500 D. 600 11、如图,E 是⊙O 内接四边形 ABCD 两条对角线的交点,CD 延长线与过 A 点的⊙ O 的切线交于F 点,若 ∠ABD=440,∠AED=1000 ,弧AD=弧AB , 则∠AFC 的度数为( ) A.780 B.920 C.560 D. 1450 C B A D C B A D P O C B D E O A F B P C O A C B D A P O A E B C O D
弦切角定理证明方法 弦切角定理证明方法连oc、oa,则有oc⊥cd于点c。得oc‖ad,知∠oca=∠cad。 而∠oca=∠oac,得∠cad=∠oac。进而有∠oac=∠bac。 由此可知,0a与ab重合,即ab为⊙o的直径。 连接bc,且作ce⊥ab于点e。立即可得△abc为rt△,且∠acb=rt∠。 由射影定理有ac2=ae*ab。又∠cad=∠cae,ac公用,∠cda=∠cea,得△cea ≌△cda,有ad=ae,所以,ac2=ab*ad。 第一题重新证明如下: 首先证明弦切角定理,即有∠acd=∠cba。
连接oa、oc、bc,则有 ∠acd+∠aco=90° = = =∠aco+∠aoc, 所以∠acd=∠aoc, 而∠cba=∠aoc, 得∠acd=∠cba。 另外,∠acd+∠cad=90°,∠cad=∠cab, 所以有∠cab+∠cba=90°,得∠bca=90°,进而ab为⊙o的直径。 2 证明一:设圆心为o,连接oc,ob,。 ∵∠tcb=90-∠ocb ∵∠boc=180-2∠ocb ∴,∠boc=2∠tcb ∵∠boc=2∠cab ∴∠tcb=∠cab 证明已知:ac是⊙o的弦,ab是⊙o 的切线,a为切点,弧是弦切角∠bac所夹的弧.
求证: 证明:分三种情况: 圆心o在∠bac的一边ac上 ∵ac为直径,ab切⊙o于a, ∴弧cma=弧ca ∵为半圆, ∴∠cab=90=弦ca所对的圆周角圆心o在∠bac的内部. 过a作直径ad交⊙o于d, 若在优弧m所对的劣弧上有一点e 那么,连接ec、ed、ea 则有:∠ced=∠cad、∠dea=∠dab ∴∠cea=∠cab ∴ 圆心o在∠bac的外部, 过a作直径ad交⊙o于d 那么∠cda+∠cad=∠cab+∠cad=90 ∴∠cda=∠cab ∴ 编辑本段弦切角推论 推论内容 若两弦切角所夹的弧相等,则这两
《切线性质与判定》练习题 一.选择题(共12小题) 1.如图,AB是⊙O的弦,PA是⊙O的切线,若∠PAB=40°,则∠AOB=() A.80° B.60° C.40° D.20° 2.如图,AB、AC是⊙O的两条弦,∠A=35°,过C点的切线与OB的延长线交于点D,则∠D的度数为() A.20° B.30° C.35° D.40° 第1题图第2题图第3题图 3.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于()A.20° B.30° C.40° D.50° 4.如图,PA、PB切⊙O于A、B两点,∠APB=80°,C是⊙O上不同于A、B的任一点,则∠ACB等于() A.80° B.50°或130° C.100° D.40° 第4题图第5题图第6题图 5.如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是() A.(5,3) B.(3,5)C.(5,4)D.(4,5) 6.如图,PC是⊙O的切线,切点为C,割线PAB过圆心O,交⊙O于点A、B,PC=2,PA=1,则PB的长为() A.5 B.4 C.3 D.2 7.如图,在同心圆中,大圆的弦AB切小圆于点C,AB=8,则圆环的面积是() A.8 B.16 C.16π D.8π 8.如图,PA、PB、CD是⊙O的切线,切点分别是A、B、E,CD分别交PA、PB于C、D两点,若∠APB=60°,则∠COD的度数() A.50° B.60° C.70° D.75° 9.如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是() A.AB=4,AT=3,BT=5 B.∠B=45°,AB=A T C.∠B=55°,∠TAC=55° D.∠A TC=∠B 第7题图第8题图第9题图 11.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,则下列结论正确的个数是() ①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线.
第六章西姆松定理及应用 习题A 1.由西姆松定理,知L ,M ,N 三点共线,注意到P ,L ,N ,B 及P ,M ,C ,L 分别四点共圆,知LPN B ∠=∠,LPM C ∠=∠.又由张角定理,有() sin sin sin B C B C PL PM PN ∠+∠∠∠= + ,即 sin sin sin mn A ln B lm C ?∠=?∠+?∠再应用正弦定理,得mn a ln b lm c ?=?+?. 2.根据直径所对的圆周角是直角,知90BDP ADP ∠=∠=?,90BFP CFP ∠=∠=?,90CEP AEP ∠=∠=?,即知D ,A ,B ;B ,F ,C ;C ,E ,A 分别三点共线. 又PD AB ⊥于D ,PE AC ⊥于E ,PF BC ⊥于F ,P 是ABC △外接圆周上一点,由西姆松定理,知D ,E ,F 三点共线. 3.延长BE ,CD 相交于点K ,延长CG ,BF 相交于点L .设CG 与BE 相交于点I ,则I 为ABC △的 内心.由12CAI BAC ∠=∠,而()11 909022 CKI CIK B C BAC ∠=?-∠=?-∠+∠=∠,从而A ,I ,C , K 四点共圆. 又AD CK ⊥于D ,AE KB ⊥于E ,AG CI ⊥于G ,A 是ICK △外接圆上任一点,由西姆松定理,知D ,E ,G 三点共线.同理,B ,I ,A ,L 四点共圆,AE BI ⊥于E ,AG IL ⊥于G ,AF BL ⊥于F ,由西姆松定理,知E ,G ,F 三点共线.故F ,G ,E ,D 四点共线. 4.设正ABC △外接圆弧?AB 上任一点P 到边BC ,CA ,AB 的距离分别为a h ,b h ,c h ,其垂足分别为 D , E , F ,正三角形边长为a .由面积等式可得a b c h h h +-= .此式两边平方,得 ()2222324 a b c a b b c a c h h h h h h h h h a +++--=. 由 sin sin b a h h PAC PBD PA PB =∠=∠=,有a b h PA h PB ?=?. 同理,a c h PA h PC ?=?,故a b h PA h PB k PC ?=?=?. 又P ,F ,E ,A 及P ,D ,B ,F 分别四点共圆,有PFD PBD PAC ∠=∠=∠,PDF PBF PCA ∠=∠=∠, 得PFD PAC △△≌,故c h PA a DF = ?,同理,a h PB a DE =?,b h PC a EF =?,即 a c b a c b h h h h h h k EF DE EF ???===由西姆松定理,知D ,E ,F 共线,即DF FE DE +=.于是 £()0a b a c b c hb h h h h h h DE DF EF k ? ---=--=?, 故222234 a b c h h h a ++=. 5.设以ABC △的三个顶点为圆心的三圆,皆经过同一点M ,而M 在ABC △的外接圆上,A e 与B e 另交于D ,A e 与C e 另交于E ,B e 与C e 另交于F . 注意到A e 与B e 中,公共弦MD ⊥连心线AB ;A e 与C e 中,公共弦ME ⊥连心线AC ;B e 与C e 中,公共弦MF ⊥连心线BC .对ABC △及其外接圆周上一点M ,应用西姆松定理,知D ,E ,F 三点共线. 习题B 1.(Ⅰ)设从点P 向BC ,CA ,AB 作垂线,垂足分别为X ,Y ,Z .由对称性,知XY 为PUV △的中位线,故UV XY ∥同理,VW YZ ∥,WU XZ ∥.由西姆松定理,知X ,Y ,Z 三点共线,故U ,V ,W 三点共线.
切线长定理—知识讲解 【学习目标】 1.了解切线长定义,掌握切线长定理; 2.了解圆外切四边形定义及性质; 3. 利用切线长定理解决相关的计算和证明. 【要点梳理】 要点一、切线长定理 1.切线长: 经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 要点诠释: 切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理: 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释: 切线长定理包含两个结论:线段相等和角相等. 要点二、圆外切四边形的性质 1.圆外切四边形 四边形的四条边都与同一个圆相切,那这个四边形叫做圆的外切四边形. 2.圆外切四边形性质 圆外切四边形的两组对边之和相等. 【典型例题】 类型一、切线长定理 1.(2015秋?湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D. (1)若PA=6,求△PCD的周长. (2)若∠P=50°求∠DOC. 【答案与解析】 解:(1)连接OE, ∵P A、PB与圆O相切, ∴PA=PB=6, 同理可得:AC=CE,BD=DE, △PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切, ∴∠OAP=∠OBP=90°∠P=50°, ∴∠AOB=360°﹣90°﹣90°﹣50°=130°, 在Rt△AOC和Rt△EOC中, , ∴Rt△AOC≌Rt△EOC(HL), ∴∠AOC=∠COE, 同理:∠DOE=∠BOD, ∴∠COD=∠AOB=65°. 【总结升华】本题考查的是切线长定理和全等三角形的判定和性质,掌握切线长定理是解题的关键. 2.如图,△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,E为BC中点. 求证:DE是⊙O切线. 【答案与解析】 连结OD、CD,AC是直径,∴OA=OC=OD,∴∠OCD=∠ODC, ∠ADC=90°,∴△CDB是直角三角形. ∵E是BC的中点,∴DE=EB=EC,∴∠ECD=∠EDC,∠ECD+∠OCD=90°, ∴∠EDC+∠ODC=90°,即OD⊥ED, ∴DE是⊙O切线. 【总结升华】自然连接OD,可证OD⊥DE. 举一反三: 【变式】已知:如图,⊙O为ABC ?的外接圆,BC为⊙O的直径,作射线BF,使得BA平分CBF ∠,过点A作AD BF ⊥于点D.求证:DA为⊙O的切线. F C F C 【答案】连接AO. ∵ AO BO =,∴ 23 ∠=∠.
西姆松(Simson)定理 西姆松定理说明 过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线。(此线常称为西姆松线) 西姆松定理的逆定理若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上。 相关的结果有: (1)称三角形的垂心为H。西姆松线和PH的交点为线段PH的中点,且这点在九点圆上。 (2)两点的西姆松线的交角等于该两点的圆周角。 (3)若两个三角形的外接圆相同,这外接圆上的一点P对应两者的西姆松线的交角,跟P的位置无关。 (4)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。 证明 证明一:△ABC外接圆上有点P,且PE⊥AC于E,PF⊥AB于F,PD⊥BC 于D,分别连DE、DF. 易证P、B、F、D及P、D、C、E和A、B、P、C分别共圆,于是∠FDP=∠A CP ①,(∵都是∠ABP的补角)且∠PDE=∠PCE ②而∠ACP+∠PCE=180° ③∴∠FDP+∠PDE=180° ④即F、D、E共线. 反之,当F、D、E共线时,由④→②→③→①可见A、B、P、C共圆. 证明二:如图,若L、M、N三点共线,连结BP,CP, 则因PL垂直于BC,PM垂直于AC,PN垂直于AB,有B、P、 L、N和M、P、L、C分别四点共圆,有 ∠PBN = ∠PLN = ∠PLM = ∠PCM. 故A、B、P、C四点共圆。 若A、B、P、C四点共圆,则∠PBN = ∠PCM。因PL 垂直于BC,PM垂直于AC,PN垂直于AB,有B、P、L、N 和M、P、L、C四点共圆,有 ∠PBN =∠PLN =∠PCM=∠PLM. 故L、M、N三点共线。
切线长定理、弦切角定理、切割线定理、相交弦定理 以及与圆有关的比例线段 [学习目标] 1.切线长概念 切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。(PA 长) 2.切线长定理 对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。 直线AB 切⊙O 于P ,PC 、PD 为弦,图中几个弦切角呢?(四个) 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。 5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。 6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。 7.与圆有关的比例线段 定理 图形 已知 结论 证法 相交弦定理 ⊙O 中,AB 、CD 为弦,交于P. PA·PB=PC·PD . 连结AC 、BD ,证:△APC∽△DPB . 相交弦定理的推论 ⊙O 中,AB 为直径,CD⊥AB 于P. PC 2 =PA·PB . (特殊情况) 用相交弦定理.
切割线定理 ⊙O 中,PT 切⊙O 于T ,割线PB 交⊙O 于A PT 2 =PA·PB 连结TA 、TB ,证:△PTB∽△PAT 切割线定理推论 PB 、PD 为⊙O 的两条割线,交⊙O 于A 、C PA·PB=PC·PD 过P 作PT 切⊙O 于T ,用两次切割线定理 (记忆的方法方法) 圆幂定理 ⊙O 中,割线PB 交⊙O 于A ,CD 为弦 P'C·P'D =r 2 -OP'2 PA·PB=OP 2-r 2 r 为⊙O 的半径 延长P'O 交⊙O 于M ,延 长OP'交⊙O 于N ,用相交 弦定理证;过P 作切线用切割线定理勾股定理证 8.圆幂定理:过一定点P 向⊙O 作任一直线,交⊙O 于两点,则自定点P 到两交点的两条线段之积为常数||(R 为圆半径),因为叫做点对于⊙O 的幂,所以将上述定理统称为圆幂定理。 【典型例题】 例1.如图1,正方形ABCD 的边长为1,以BC 为直径。在正方形内作半圆O ,过A 作半圆切线,切点为F ,交CD 于E ,求DE :AE 的值。 图1 解:由切线长定理知:AF =AB =1,EF =CE 设CE 为x ,在Rt△ADE 中,由勾股定理 ∴, ,
切线长定理及其应用 一、基础知识总结 1.内切圆和内心 定义: 与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心是三角形三条角平分 线的交点,叫做三角形的内心. 总结:判断一个多边形是否有内切圆,就是判断能否找到一个点到各边距离都 相等。 2.直角三角形的内切圆半径与三边关系 (1)一个基本图形; (2)两个结论: 1)四边形OECF 是正方形 2)r=(a+b-c)∕2或r=ab ∕(a+b+c) (3)两个方法 代数法(方程思想);面积法 3.切线长定义:过圆外一点作圆的切线,该点和切点之间的线段长叫做切线长。 4.切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的交角。 二、典型例题解析 【例1】如图△ABC 的内切圆⊙O 与BC 、CA 、AB 分别相交于点D 、E 、F ,且AB=9 cm,BC=14 cm ,CA=13 cm ,求AF 、BD 、CE 的长 D E F O C B A 112 12902 a b c A B C A B C S s r p a b c p C r a b c ?∠∠∠==++∠=?=+-设、、分别为中、、的对边,面积为,则内切圆半径(),其中(); (),则()
【例2】如图,已知⊙O是△ABC的内切圆,切点为D、 E、F,如果AE=1, CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r. 【例3】如图,以等腰ABC ?中的腰A B为直径作⊙O,交底边BC于点D.过点D作⊥,垂足为E. D E A C (I)求证:D E为⊙O的切线; (II)若⊙O的半径为5,60 ∠= ,求D E的长. B A C 【例4】如上图等边三角形的面积为S,⊙O是它的外接圆,点P是⌒BC的中点.(1)试判断过C所作的⊙O的切线与直线AB是否相交,并证明你的结论;(2)设直线 CP与AB相交于点D,过点B作BE⊥CD垂足为E,证明BE是⊙O的切线,并求△ BDE的面积.
平面几何定理及其证明 梅涅劳斯定理 1 .梅涅劳斯定理及其证明 定理:一条直线与 ABC 的三边AB BC CA 所在直线分别交于点 D E 、F ,且D E 、F 均 证明:如图,过点C 作AB 的平行线,交EF 于点G. 因为 CG // AB ,所以 CG CF --------------------- ( 1) AD FA 因为 CG // AB ,所以 EC ( 2) DB BE C F ,即得 A D C F EC FA DB EC FA 2.梅涅劳斯定理的逆定理及其证明 定理:在 ABC 的边AB BC 上各有一点 D E ,在边 AC 的延长线上有一点 F ,若 二、 塞瓦定理 3 .塞瓦定理及其证明 定理:在ABC 内一点P,该点与ABC 的三个顶点相连所在的 三条直线分别交 ABCE 边AB BC CA 于点D E 、F ,且D E 、F 三点均不是 ABC 不是ABC 的顶点,则有 AD BE CF 1 DB EC 由(1)宁(2) DB 可得兀 AD BE CF DB EC FA 1 ,那么,D E 、F 三点共线. 证明:设直线EF 交AB 于点D ,则据梅涅劳斯定理有 AD / BE CF 丽 EC FA 因为AD Bl CF DB EC FA 1,所以有誥 段AB 上,所以点D 与D 重合.即得D 鴿.由于点D D 都在线 E 、F 三点共线. 证明: 运用面积比可得 AD DB S ADP S BDP S ADC S BDC 根据 等 比定理有 S ADP S ADC S ADC S ADP S APC S S BDP BDC S BDC S BDP S
圆的知识点总结 (一)圆的有关性质 [知识归纳] 1. 圆的有关概念: 圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆; 弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高; 圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆;圆心角、圆周角、圆内接四边形的外角。 2. 圆的对称性 圆是轴对称图形,经过圆心的每一条直线都是它的对称轴,圆有无数条对称轴; 圆是以圆心为对称中心的中心对称图形; 圆具有旋转不变性。 3. 圆的确定 不在同一条直线上的三点确定一个圆。 4. 垂直于弦的直径 垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧; 推论1 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。 垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个,就 可推出另外三个:①过圆心;②垂直于弦;③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧。 1
推论2圆的两条平行弦所夹的弧相等。 5. 圆心角、弧、弦、弦心距之间的关系 定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。 推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。 此定理和推论可以理解成:在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆 心角或两条弧所对的弦相等;④两条弦的弦心距相等。 圆心角的度数等于它所对的弧的度数。 6. 圆周角 定理一条弧所对的圆周角等于它所对的圆心角的一半; 推论1同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等; 推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径; 推论3如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。 圆周角的度数等于它所对的弧的度数的一半。 7. 圆内接四边形的性质 圆内接四边形的对角互补,并且任何一个外角都等于它的内对角。 ※8. 轨迹 轨迹符合某一条件的所有的点组成的图形,叫做符合这个条件的点的轨迹。 (1)平面内,到一定点的距离等于定长的点的轨迹,是以这个定点为圆心,定长为半径的圆; (2)平面内,和已知线段两个端点的距离相等的点的轨迹,是这条线段的垂直平分线; (3)平面内,到已知角两边的距离相等的点的轨迹,是这个角的平分线。 [例题分析] 例1. 已知:如图1,在⊙O中,半径OM⊥弦AB于点N。 图1 ①若AB =,ON=1,求MN的长; ②若半径OM=R,∠AOB=120°,求MN的长。 解:①∵AB =,半径OM⊥AB,∴AN=BN = ∵ON=1,由勾股定理得OA=2 ∴MN=OM-ON=OA-ON=1 ②∵半径OM⊥AB,且∠AOB=120°∴∠AOM=60° 2
第六章西姆松定理及应用 【基础知识】 西姆松定理 过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足点共线(此线常称为西姆松线). 证明如图6-1,设P 为ABC △的外接圆上任一点,从P 向三边BC ,CA ,AB 所在直线作垂线,垂足分别为L ,M ,N .连PA ,PC ,由P ,N ,A ,M 四点共圆,有 β α γ βL M A P B N C 图6-1 PMN PAN PAB PCB PCL ∠=∠=∠=∠=∠. 又P ,M ,C ,L 四点共圆,有PML PCL ∠=∠. 故PMN PML ∠=∠,即L ,N ,M 三点共线. 注 此定理有许多证法.例如,如下证法: 如图6-1,连PB ,令PBC α∠=,PCB β∠=, PCM γ∠=,则 PAM α∠=,PAN β∠=,PBN γ∠=,且cos BL PB α=?,cos LC PC β=?,cos CM PC γ=?, cos MA PA α=?,cos AN PA β=?,cos NB PB γ=?.对ABC △,有 cos cos cos 1cos cos cos BL CM AN PB PC PA LC MA NB PC PA PB αγββαγ ?????=??=???.故由梅涅劳斯定理之逆定理,知L ,N ,M 三点共线. 西姆松定理还可运用托勒密定理、张角定理、斯特瓦尔特定理来证(略). 西姆松定理的逆定理 若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上. 证明如图6-1,设点P 在ABC △的三边BC ,CA ,AB 所在直线上的射影分别为L ,M ,N ,且此三点共线.由PN AB ⊥于N ,PM AC ⊥于M ,PL BC ⊥于L ,知P ,B ,L ,N 及P ,N ,A ,M 分别四点共圆,而AB 与LM 相交于N ,则PBC PBL PNM PAM ∠=∠=∠=∠,从而P ,B ,C ,A 四点共圆,即点P 在ABC △的外接圆上. 【典型例题与基本方法】 1.找到或作出三角形外接圆上一点在三边上的射影,是应用西姆松定理的关键 例1如图6-2,过正ABC △外接圆的AC 上点P 作PD ⊥直线AB 于D ,作P E A C ⊥于E ,作P F B C ⊥于F .求证: 111 PF PD PE += .
一、填空 1.已知:如图7-143,直线BC切⊙O于B点,AB=AC,AD=BD,那么∠A=____. 2.已知:如图7-144,直线DC与⊙O相切于点C,AB为直径,AD⊥DC于D,∠DAC=28°,则∠CAB=____ . 3.已知:如图7-145,PA切⊙O于点A,∠P=15°,∠ABC=47°,则∠C= ____. 4.已知:如图7-146,三角形ABC的∠C=90°,内切圆O与△ABC的三边分别切于D,E,F三点,∠DFE=56°,那么∠B=____. 二、选择 5.已知:△ABC内接于⊙O,∠ABC=25°,∠ACB= 75°,过A点作⊙O的切线交BC的延长线于P,则∠APB等于() A.62.5°B.55° C.50°D.40° 6.已知:如图 7-149,PA,PB切⊙O于A,B两点,AC为直径, 则图中与∠PAB相等的角的个数为() A.1 个B.2个C.4个D.5个 7.已知如图7-150,四边形ABCD为圆内接四边形,AB是直径, MN切⊙O于C点,∠BCM=38°,那么∠ABC的度数是 A.38°B.52°C.68°D.42° 三、解答 8.已知:如图7-152,PT与⊙O切于C,AB为直径,∠BAC=60°, AD为⊙O一弦.求∠ADC与∠PCA的度数. 9.已知:如图7-154,⊙O的半径OA⊥OB,过A点的直线交OB于 P,交⊙O于Q,过Q引⊙O的切线交OB延长线于C,且PQ=QC.求 ∠A的度数.
10.已知:如图7-160,AC是⊙O直径,PA⊥AC于A,PB切⊙O于B,BE⊥AC于E.若AE=6cm,EC=2cm,求BD的长. 2 11.已知:如图7-185,∠1=∠2,⊙O过A,D两点且交AB,AC于E,F,BC切⊙O于D.求证:EF∥BC. 12.已知:如图7-176,圆内接四边形ABCD的AB边经过圆心,AD,BC的延长线相交于E,过C点的切线CF⊥AE于F.求证: (1)△ABE为等腰三角形; (2)若 BC=1cm,AB=3cm,求EF的长.
中考复习专题——切线长定理与弦切角定理 【知识要点】 1.切线长定理:过圆外一点P做该圆的两条切线,切点为A、B。AB交PO于点C,则有如下结论: (1)PA=PB (2)PO⊥AB,且PO平分AB (3)APO BPO OAC OBC ∠=∠=∠=∠;AOP BOP CAP CBP ∠=∠=∠=∠ 2.弦切角定理:弦切角(切线与圆的夹角)等于它所夹的弧所对的圆周角 推论:若两弦切角所夹的弧相等,则这两个弦切角也相等 【典型例题】 【例1】如图1,AB,AC是⊙O的两条切线,切点分别为B、C、D是优弧BC上的点,已知∠BAC=800,那么∠BDC =______. 图1 图2 图3 举一反三: 1.如图2,AB是⊙O的弦,AD是⊙O的切线,C为AB上任一点,∠ACB=1080,那么∠BAD =______. 2.如图3,PA,PB切⊙O于A,B两点,AC⊥PB,且与⊙O相交于D,若∠DBC=220,则∠APB=________.【例2】如图,已知圆上的弧AC BD =,过C点的圆的切线与BA的延长线交于E点,证明: (1)∠ACE=∠BCD; (2)BC2=BE×CD. 举一反三: 1.如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB C B O A D C B A D P O
P B A O 的延长线于点C ,若DA =DC ,求证:AB =2BC . 【例3】已知:如图 7-149,PA ,PB 切⊙O 于A ,B 两点,AC 为直径,则图中与∠PAB 相等的角的个数为 A .1 个; B .2个; C .4个; D . 5个. 【例4】如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长. 举一反三: 1. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°. (1)求∠APB 的度数; (2)当OA =3时,求AP 的长. 2.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的长.
初三数学 有关圆的经典例题 1. 在半径为的⊙中,弦、的长分别为和,求∠的度数。132O AB AC BAC 分析:根据题意,需要自己画出图形进行解答,在画图时要注意AB 与AC 有不同的位置关系。 解:由题意画图,分AB 、AC 在圆心O 的同侧、异侧两种情况讨论, 当AB 、AC 在圆心O 的异侧时,如下图所示, 过O 作OD ⊥AB 于D ,过O 作OE ⊥AC 于E , ∵,,∴,AB AC AD AE = == = 32322 2 ∵,∴∠,OA OAD AD OA == =132 cos cos ∠OAE AE OA = = 22 ∴∠OAD=30°,∠OAE=45°,故∠BAC=75°, 当AB 、AC 在圆心O 同侧时,如下图所示, 同理可知∠OAD=30°,∠OAE=45°, ∴∠BAC=15° 点拨:本题易出现只画出一种情况,而出现漏解的错误。 例2. 如图:△ABC 的顶点A 、B 在⊙O 上,⊙O 的半径为R ,⊙O 与AC 交于D , 如果点既是的中点,又是边的中点,D AB AC ? (1)求证:△ABC 是直角三角形; ()22 求的值AD BC 分 析 : ()1由为的中点,联想到垂径定理的推论,连结交于,D AB OD AB F ? 则AF=FB ,OD ⊥AB ,可证DF 是△ABC 的中位线;
(2)延长DO 交⊙O 于E ,连接AE ,由于∠DAE=90°,DE ⊥AB ,∴△ADF ∽△,可得·,而,,故可求DAE AD DF DE DF BC DE R AD BC 2 2 122=== 解:(1)证明,作直径DE 交AB 于F ,交圆于E ∵为的中点,∴⊥,D AB AB DE AF FB ? = 又∵AD=DC ∴∥,DF BC DF BC = 12 ∴AB ⊥BC ,∴△ABC 是直角三角形。 (2)解:连结AE ∵DE 是⊙O 的直径 ∴∠DAE=90° 而AB ⊥DE ,∴△ADF ∽△EDA ∴ ,即·AD DE DF AD AD DE DF ==2 ∵,DE R DF BC ==21 2 ∴·,故AD BC R AD BC R 2 2 == 例3. 如图,在⊙O 中,AB=2CD ,那么( ) A A B CD B AB CD ..?>? ?
平面几何中的四个重要定理 梅涅劳斯(Menelaus ) 定理(梅氏线) △ ABC 的三边BC 、CA 、AB 或其延长线上有点 P 、Q 、R ,贝U P 、Q 、R 共线的充 塞瓦(Ceva )定理(塞瓦点) △ ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,贝U AP 、BQ 、CR 共点的充要条件 西姆松(Simson )定理(西姆松线) 从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接 要条件是 BP CQ AR 1 PC QA RB 是BP 殂塑1。 PC QA RB P 圆 。
-可编辑- 圆上。 例题: 1、设AD 是厶ABC 的边BC 上的中线,直线CF 交AD 于F 。求 、 AE 2AF 证:—— ED FB AE DC BF 【分析】CEF 截厶ABD T -------------------------- 1 (梅氏定理) ED CB FA 【评注】也可以添加辅助线证明:过 A 、B 、D 之一作CF 的平 行线。 【分析】连结并延长 AG 交BC 于M ,贝U M 为BC 的中点。 BE CF GM (DB DC) = GM 2MD EA FA = AG MD 2GM MD AB 、AC 于 E 、F ,交 CB 于 D 。 求证: BE CF 1。 EA FA DEG 截厶 ABM T DGF 截厶 ACM T BE AG MD EA GM DB CF AG MD FA GM DC 1 (梅氏定理) 1 (梅氏定理) A 2、过△ ABC 的重心G 的直线分别交
5、已知△ ABC 中,/ B=2 / C 。求证: 【评注】梅氏定理 【评注】梅氏定理 CG 相交于一点。 【分析】 【评注】塞瓦定理 3、D 、E 、F 分别在△ ABC 的 BC 、 匹圧些,AD 、BE 、 DC FB EA 【分析】 4、以△ ABC 各边为底边向外作相似的等腰厶 BCE 、△ CAF 、△ ABG 。求证: AE 、BF 、