一种新的三项共轭梯度法求解非线性方程组
- 格式:pdf
- 大小:716.63 KB
- 文档页数:8

共轭梯度法公式
共轭梯度法是一种用于求解线性方程组的迭代算法。
其主要思想是通过利用前一次迭代的信息来加速当前迭代的速度,从而减少迭代次数和计算量。
共轭梯度法公式包括以下几个步骤:
1. 初始化:设初始解为x0,残量b0为Ax0-b,共轭方向d0=b0。
2. 迭代求解:对于第k次迭代,计算步长αk,使得xk+1=xk+αkd,其中d是共轭方向,满足dTkAd=0,即d是A的共轭向量。
3. 更新残量:计算新的残量bk+1=Axk+1-b,如果bk+1小于预设精度,则停止迭代。
4. 更新共轭方向:计算新的共轭方向dk+1=bk+1+βkdk,其中βk=(bk+1)Tbk+1/(bk)Tbk,保证dk+1与之前的共轭方向都是A的共轭向量。
5. 重复迭代,直到满足收敛条件,返回最终解xk+1。
共轭梯度法是一种高效的求解大型线性方程组的方法,尤其适用于稀疏矩阵和对称正定矩阵。
公式简单易懂,容易实现,且具有较快的收敛速度。
- 1 -。

共轭梯度法步骤共轭梯度法是一种求解线性方程组的迭代算法,它以高效稳定的特点而广受欢迎。
以下是共轭梯度法的步骤:步骤1:初始化首先,我们需要有一个初始向量x0和一个初始残量r0=b-Ax0。
其中,A为系数矩阵,b为常数向量。
步骤2:计算方向向量令d0=r0,表示第一次迭代的方向向量。
步骤3:计算步进长度令α0=(r0·r0)/(d0·Ad0),其中·表示向量的点积。
α0表示迭代过程中每个方向向量的步进长度。
步骤4:更新解向量令x1=x0+α0d0,表示迭代后的解向量。
步骤5:计算新残量令r1=r0-α0Ad0。
步骤6:判断终止条件如果r1的范数小于预设阈值,或者迭代次数达到预设次数,终止迭代。
否则,进入下一次迭代。
步骤7:更新方向向量令β1=(r1·r1)/(r0·r0),表示更新方向向量的轴线。
步骤8:计算新方向向量令d1=r1+β1d0,表示新的迭代方向向量。
步骤9:计算新的步进长度令α1=(r1·r1)/(d1·Ad1)。
步骤10:更新解向量令x2=x1+α1d1。
步骤11:更新残量令r2=r1-α1Ad1。
步骤12:重复步骤6至11,直至满足终止条件。
总结起来,共轭梯度法的步骤主要包括初始化、计算方向向量、计算步进长度、更新解向量、计算新残量、判断终止条件、更新方向向量、计算新的步进长度、更新解向量和更新残量等。
该算法迭代次数较少,收敛速度快,适用于大规模线性方程组的求解。

共轭梯度法例题详解共轭梯度法是一种用于求解线性方程组的迭代方法。
它的基本思想是利用一组共轭的搜索方向来逐步逼近线性方程组的解。
下面我将从多个角度详细解释共轭梯度法的例题。
首先,让我们考虑一个简单的例子。
假设我们要求解一个二维线性方程组 Ax = b,其中 A 是一个对称正定矩阵,x 和 b 是列向量。
共轭梯度法的步骤如下:1. 初始化 x0 和 r0,其中 x0 是初始解向量,r0 是初始残差向量,r0 = b Ax0。
2. 初始化搜索方向 p0 = r0。
3. 迭代计算:a. 计算步长 alpha = (r_k^T r_k) / (p_k^T A p_k),其中 k 表示第 k 次迭代。
b. 更新解向量,x_(k+1) = x_k + alpha p_k。
c. 更新残差向量,r_(k+1) = r_k alpha A p_k。
d. 计算 beta = (r_(k+1)^T r_(k+1)) / (r_k^T r_k)。
e. 更新搜索方向,p_(k+1) = r_(k+1) + beta p_k。
4. 重复步骤 3 直到满足收敛条件。
这是共轭梯度法的基本算法。
下面我们通过一个具体的例子来说明。
假设我们要求解以下线性方程组:3x + 2y = 9。
2x + 5y = -4。
将其转化为矩阵形式,Ax = b,其中。
A = [[3, 2],。
[2, 5]],。
x = [[x],。
[y]],。
b = [[9],。
[-4]].首先,我们需要判断矩阵 A 是否是对称正定矩阵。
对于本例中的 A,它是对称矩阵且特征值为正,因此满足条件。
接下来,我们进行共轭梯度法的迭代计算。
假设初始解向量 x0 = [[0], [0]],初始残差向量 r0 = b Ax0 = [[9], [-4]]。
初始化搜索方向 p0 = r0。
第一次迭代:计算步长 alpha = (r0^T r0) / (p0^T A p0) = (81 + 16) / (9 + 20) = 97 / 29 ≈ 3.34。

牛顿法、拟牛顿法、高斯-牛顿法、共轭梯度
法推导总结
一、牛顿法
牛顿法是一种求解非线性方程的迭代方法。
牛顿法的基本思想是:在当前点附近,用一次泰勒展开式近似原函数,然后求解近似函数的极值点。
牛顿法每次迭代所需要的计算量较大,但其收敛速度较快。
二、拟牛顿法
拟牛顿法是一种求解无约束极值问题的优化算法。
拟牛顿法是将牛顿法中Hessian矩阵用近似Hessian矩阵Bk表示的算法。
拟牛顿法的计算量比牛顿法小,但是收敛速度较牛顿法慢。
三、高斯-牛顿法
高斯-牛顿法是求解非线性最小二乘问题的一种迭代算法。
该算法假设误差服从高斯分布,利用牛顿法求解目标函数的局部极小值,以最小化残差平方和。
高斯-牛顿法在处理非线性最小二乘问题时具有很好的收敛性。
四、共轭梯度法
共轭梯度法是解决对称正定线性方程组的迭代算法。
该算法通过对一个对称正定矩阵进行迭代求解,寻找线性方程组的解。
共轭梯度法的优点是可以使用较少的内存和计算量实现高效的求解。
以上算法都是数值优化中比较常用的算法,它们各自具有不同的优缺点,可根据实际问题的特点来选择合适的算法。

最速下降法1.最速下降方向函数f(x)在点x处沿方向d的变化率可用方向导数来表示。
对于可微函数,方向导数等于梯度与方向的内积,即:Df(x;d) = ▽f(x)T d,因此,求函数f(x)在点x处的下降最快的方向,可归结为求解下列非线性规划:min ▽f(x)T ds.t. ||d|| ≤ 1当 d = -▽f(x) / ||▽f(x)||时等号成立。
因此,在点x处沿上式所定义的方向变化率最小,即负梯度方向为最速下降方向。
2.最速下降算法最速下降法的迭代公式是x(k+1) = x(k) + λk d(k) ,其中d(k)是从x(k)出发的搜索方向,这里取在x(k)处的最速下降方向,即d = -▽f(x(k)).λk是从x(k)出发沿方向d(k)进行一维搜索的步长,即λk满足f(x(k) + λk d(k)) = min f(x(k)+λd(k)) (λ≥0).计算步骤如下:(1)给定初点x(1) ∈ R n,允许误差ε> 0,置k = 1。
(2)计算搜索方向d = -▽f(x(k))。
(3)若||d(k)|| ≤ε,则停止计算;否则,从x(k)出发,沿d(k)进行一维搜索,求λk,使f(x(k) + λk d(k)) = min f(x(k)+λd(k)) (λ≥0).(4)令x(k+1) = x(k) + λk d(k),置k = k + 1,转步骤(2)。
共轭梯度法1.共轭方向无约束问题最优化方法的核心问题是选择搜索方向。
以正定二次函数为例,来观察两个方向关于矩阵A共轭的几何意义。
设有二次函数:f(x) = 1/2 (x - x*)T A(x - x*) ,其中A是n×n对称正定矩阵,x*是一个定点,函数f(x)的等值面1/2 (x - x*)T A(x - x*) = c是以x*为中心的椭球面,由于▽f(x*) = A(x - x*) = 0,A正定,因此x*是f(x)的极小点。



共轭梯度法原理共轭梯度法是一种用于求解大型稀疏线性方程组的优化算法。
它是一种迭代法,通过寻找一个搜索方向,并在该方向上进行搜索,逐步逼近最优解。
共轭梯度法在优化问题中有着广泛的应用,尤其在求解大规模线性方程组时表现出色。
共轭梯度法的原理可以从最小化函数的角度进行解释。
假设我们要最小化一个二次函数f(x),其中x是一个n维向量。
共轭梯度法的目标是找到一个搜索方向d,使得沿着这个方向移动能够让函数值最小化。
在每一步迭代中,我们需要找到一个合适的步长α,使得沿着搜索方向d移动后能够使函数值减小最快。
共轭梯度法的核心思想是利用历史信息来加速收敛。
在每一步迭代中,共轭梯度法会根据历史搜索方向的信息来选择当前的搜索方向,以便更快地找到最优解。
这种方法可以在较少的迭代次数内找到最优解,尤其对于大规模问题来说,可以节省大量的计算资源。
在实际应用中,共轭梯度法通常用于求解线性方程组Ax=b,其中A是一个对称正定矩阵。
共轭梯度法的迭代过程可以通过以下步骤进行描述:1. 初始化,选择一个初始解x0,计算残差r0=b-Ax0,选择初始搜索方向d0=r0。
2. 迭代更新,在第k步迭代中,计算步长αk,更新解xk=xk-1+αkd,并计算残差rk=b-Axk。
然后根据历史搜索方向的信息,计算新的搜索方向dk= rk+βkdk-1,其中βk是一个根据历史信息计算得到的参数。
3. 收敛判断,在每一步迭代中,可以根据残差的大小来判断算法是否已经收敛。
如果残差足够小,可以停止迭代并得到近似解x。
共轭梯度法的优点在于它对存储和计算资源的要求相对较低,尤其适用于大规模稀疏线性方程组的求解。
同时,由于共轭梯度法利用了历史搜索方向的信息,可以加速收敛,节省计算时间。
然而,共轭梯度法也有一些局限性。
首先,它只适用于对称正定矩阵,对于一般的线性方程组可能不适用。
其次,共轭梯度法可能受到舍入误差的影响,在迭代过程中可能会出现数值不稳定的情况。
总的来说,共轭梯度法是一种高效的优化算法,特别适用于求解大规模稀疏线性方程组。

prp共轭梯度法
PRP共轭梯度法(Polak-Ribiére-Polyak conjugate gradient method)是一种用于求解非线性优化问题的迭代算法,也被称为非线性共轭梯度法。
它是在共轭梯度法的基础上,引入了Polak-Ribiére-Polyak条件来加速收敛。
PRP共轭梯度法的基本思想是通过迭代搜索,在每一步中沿着负梯度的方向更新当前解,并且选择一个合适的搜索方向,以加快收敛速度。
具体步骤如下:
1. 初始化:选择初始解x0,设初始搜索方向为d0=−∇f(x0)(负梯度方向)。
2. 计算步长:在当前搜索方向上,通过线搜索方法(如Armijo准则)确定步长αk,以使f(xk+αkd) 的值最小化。
3. 更新解:根据步长αk,在当前搜索方向上更新解,
xk+1=xk+αkd。
4. 计算梯度:计算新解xk+1处的梯度∇f(xk+1)。
5. 更新搜索方向:根据Polak-Ribiére-Polyak条件计算新的搜索方向dk+1=−∇f(xk+1)+βkdk,其中
βk=max{0,⟨∇f(xk+1),∇f(xk+1)−∇f(xk)⟩/⟨∇f(xk),∇f(xk)⟩} 。
6. 判断终止条件:如果满足终止条件(例如梯度的模小于一定阈值),则停止迭代;否则返回步骤2进行下一次迭代。
PRP共轭梯度法的优点是能够在有限次迭代后找到最优解,收敛速度较快。
然而,它也存在一些局限性,比如在某些情况下可能会出现震荡现象,导致迭代结果不收敛。
因此,在实际应用中,需要根据问题的特点选择合适的优化算法。

共轭梯度法算法
共轭梯度法算法是一种优化算法,用于解决大型线性方程组的求解问题。
它的核心思想是在每一步迭代中,将搜索方向沿着前一次迭代的残差与当前梯度的线性组合方向上进行,以达到更快的收敛速度。
共轭梯度法算法可以用于求解矩阵方程 Ax=b,其中 A 是一个对称正定矩阵,b 是一个列向量。
在求解过程中,需要先初始化解向量 x0 和残差向量 r0,然后通过不断迭代更新解向量和残差向量,直到满足一定的收敛条件。
共轭梯度法算法的优点是可以在迭代次数较少的情况下得到较好的解,而且不需要存储大型矩阵,可以节省内存空间。
它常被应用于求解优化问题、信号处理和机器学习等领域。
- 1 -。
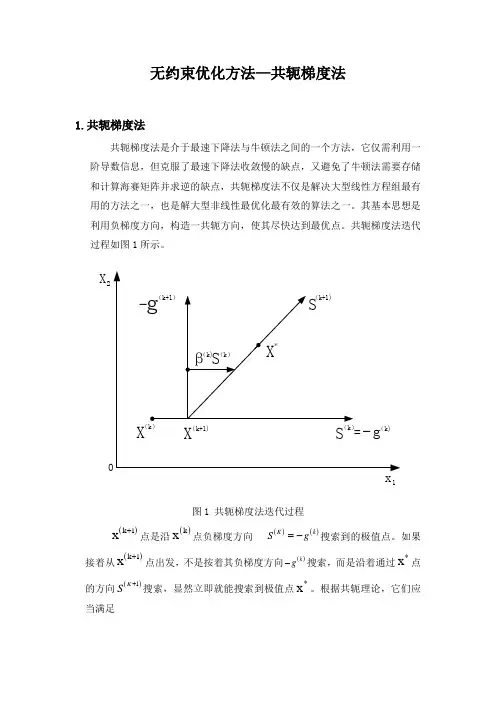
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
其基本思想是利用负梯度方向,构造一共轭方向,使其尽快达到最优点。
共轭梯度法迭代过程如图1所示。
1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。
如果接着从()k 1x +点出发,不是按着其负梯度方向()kg -搜索,而是沿着通过*x 点的方向()1K S +搜索,显然立即就能搜索到极值点*x 。
根据共轭理论,它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向,新构造的共轭方向()1K S +,可由矢量合成,()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理,推到出:()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+,就可以构造一个与梯度矢量为共轭的矢量()1K S +,沿着该方向搜索,即可求得极值点。
共轭梯度法程序框图如图2所示。
图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解,其中:初始点()0[1,1]T X =。
收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结 论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。
共轭梯度法的原理共轭梯度法是一种用于求解线性方程组的迭代方法,其原理是利用共轭方向的特性来加速收敛速度。
在实际问题中,线性方程组的求解是一项非常重要的任务,经常出现在科学计算、工程设计、物理模拟等领域。
共轭梯度法通过迭代的方式,逐步逼近方程组的解,从而提高求解效率和精度。
共轭梯度法的主要思想是将待求解的线性方程组转化为一个优化问题,通过最小化目标函数来找到最优解。
具体来说,假设有一个n 维向量x和一个n×n的矩阵A,以及一个n维向量b,我们需要求解Ax=b。
共轭梯度法的目标是找到一个n维向量x,使得目标函数f(x)最小化,其中f(x)=(1/2)x^TAx-x^Tb。
共轭梯度法的基本步骤如下:1. 初始化向量x0和残差r0=b-Ax0,设置迭代次数k=0。
2. 计算搜索方向d,d=rk+(k-1)βk-1d(k-1),其中βk-1=(rk^Trk)/(rk-1^Trk-1)。
3. 计算步长αk,αk=(rk^Trk)/(d^TAd)。
4. 更新xk=xk-1+αkd,更新残差rk=rk-1-αkAd。
5. 如果残差rk的范数小于给定的收敛条件,或达到最大迭代次数,则停止迭代;否则,返回步骤2。
共轭梯度法的优点是具有快速收敛和内存占用少的特点。
由于每次迭代都在共轭方向上前进,可以避免了梯度下降法中的zigzag现象,从而加快了收敛速度。
此外,共轭梯度法只需要存储当前迭代的向量和矩阵乘积,而不需要存储所有的迭代历史,因此内存占用较小。
然而,共轭梯度法也存在一些限制和注意事项。
首先,共轭梯度法只适用于对称正定的矩阵A,否则可能出现收敛失败的情况。
其次,共轭梯度法对初始解的选择较为敏感,不同的初始解可能导致不同的收敛速度和精度。
此外,共轭梯度法在求解大规模问题时可能需要较长的迭代时间,因此对于大规模问题,需要考虑使用并行计算的方法来加速求解过程。
共轭梯度法是一种有效的线性方程组求解方法,通过利用共轭方向的特性,可以加快收敛速度和提高求解精度。
主题:matlab共轭梯度法求解方程组近年来,随着科学技术的不断发展,数学建模和计算机仿真成为科学研究和工程技术领域的重要手段。
在实际应用中,我们常常需要解决线性方程组的求解问题,而共轭梯度法作为一种高效的迭代求解方法,广泛应用于信号处理、图像处理、地球物理勘探和优化问题等领域。
本文将介绍如何利用matlab中的共轭梯度法求解线性方程组的基本原理和实际操作方法。
1. 共轭梯度法的基本原理共轭梯度法是一种迭代法,用于求解对称正定线性方程组Ax=b。
该方法的核心思想是通过一系列的迭代操作,逐步逼近方程组的解,直到满足一定的精度要求。
在每一步迭代中,共轭梯度法利用残差和方向向量的共轭性质,不断寻找最优的步长,从而实现方程组的求解。
2. matlab中共轭梯度法的基本调用方法在matlab中,调用共轭梯度法求解线性方程组非常简单。
需要将方程组的系数矩阵A和右端向量b输入到matlab中,然后利用内置函数conjugateGradient进行求解。
具体的调用方法如下:x = conjugateGradient(A, b, x0, maxIter, tol)其中,A为系数矩阵,b为右端向量,x0为初始解向量,maxIter为最大迭代次数,tol为精度要求。
调用完毕后,matlab将返回方程组的近似解x。
3. 共轭梯度法在实际工程中的应用共轭梯度法作为一种高效的求解方法,在工程技术领域得到了广泛的应用。
以图像处理为例,图像处理中经常需要解决大规模的线性方程组,而共轭梯度法能够高效地求解这类问题,提高了图像处理算法的效率和稳定性。
另外,在地球物理勘探中,共轭梯度法也被广泛应用于三维数据的快速处理和解释。
可以说,共轭梯度法在实际工程中发挥着重要的作用。
4. 共轭梯度法的优缺点分析尽管共轭梯度法具有非常高的效率和稳定性,但是该方法也存在一些缺点。
该方法只适用于对称正定的线性方程组,对于一般的线性方程组并不适用。
共轭梯度法的收敛速度受到方程条件数的影响,对于病态问题,可能收敛速度较慢。