中国振动工程学会模态分析高级研修班讲课资料(第五章)多输入多输出系统的模态参数识别

将上式代入(5.6-14)，得
sin t m 0.325057
0
F0 1 t 1 t 0.627963 sin sin 1 t d m 1 0
F0 1 0.627963 2 sin t sin 1t 2 2 ω1 m 1 1 1
F q2 t 0 m 2 1 2 1 0.627963 2 1 cos1t 0.325057 2 1 cos 2 t 1 2
F0 k k 1 cos0.796226 t 0.044658 1 cos1.538188 t 0.621945 k m m
r t
1
t
(r 1,2,, n) (5.6-12)
任意激励Nr(t)的特解可以由卷积积分给出，即

r
N r sin r t d 0 (r 1,2,, n)
(5.6-13)
自由振动初始条件的响应 多自由度无阻尼系统对任意激振的响应求解推导 ——振型分析
也可以在坐标变换式(5.6-4)两边同时左乘uTM，得 T T 0 (5.6-11) 0 u Mq0 , η0 u Mq 由初始条件引起方程(5.6-8)的齐次解为
式中 r 0和 r阶模态在正则坐标中的初始条件。 r为第 0
r 0 r t r 0 cos r t sin r t r
T T
(5.6-5) (5.6-6)
方程(5.6-5)左乘以uT，有
T
t u Kuη t u F t u Muη
t ω η t N t η
(5.6-7) 式中N(t)=uTF(t)是与广义坐标向量(t)相应的n维广义力 向量，即正则激励。

t kuξ t 0 Muξ
由正交性得解耦的方程为
t uT kuξ t 0 uT Muξ
t K ξ t 0 Mr ξ r
(5.4-3)
式Mr为模态质量矩阵，Kr为模态刚度矩阵，它们都是对 角矩阵。
5.4 系统对初始条件的响应· 振型叠加法
mv0 1 0.459701 k q t 0.577350 sin 0.796226 t m m 0.627693 k mv0 1 0.888074 k 0.577350 sin1.538188 t m m 0.325057 k 0.265408 m k v0 sin 0.796226 t m 0.362555 k 0.512730 m k v0 sin1.53818 8 t m 0.187672 k
q t uη t
代入系统的运动微分方程，并用正则振型矩阵的转置 uT 左乘方程两边，由正交性条件得解耦方程为 t Λη t 0 η
r t r2r t 0
r 1, 2, , n
5.4 系统对初始条件的响应· 振型叠加法
r0 u
r T r T 0 Mq0 ,r0 u Mq
(r 1,2,, n) (5.4-11)
由式(5.5-4)求出原坐标q(t)的普遍表达式为
q t uη t
n
u r t u
r
r 1 n r 1
n
r
r0 sin r t r0 cos r t r
5.5 瑞利(Rayleigh)商
瑞利商法的提出意义

多自由度系统振动涉及到多个自由度的运动，其动力学行为 比单自由度系统更为复杂。掌握多自由度系统振动的基本原 理和方法，对于解决实际工程问题、提高设备性能和安全性 具有重要意义。
课程目的
理解多自由度系统振动的 特性，包括固有频率、模 态振型等。
掌握多自由度系统振动的 基本原理和数学模型。
学习多自由度系统振动的 分析方法，包括直接法、 模态法和传递矩阵法等。
控制算法则是实现控制策略的具体计算方法。常见的控制算法包 括PID控制、状态反馈控制、最优反馈控制等。这些算法可以根 据系统的特性和要求进行选择和优化。
05
多自由度系统振动应用
机械系统振动控制
机械系统中的多自由度振动问题广泛存在，如旋转机械、往复机械和柔性机械等 。控制这些振动可以提高机械系统的稳定性和可靠性，减少磨损和疲劳，延长使 用寿命。
多自由度系统振动
CONTENTS
• 引言 • 多自由度系统振动基础 • 多自由度系统振动特性 • 多自由度系统振动控制 • 多自由度系统振动应用 • 课程总结与展望
01
引言
课程背景
机械系统振动是工程领域中常见的问题，多自由度系统振动 更是其中的重要分支。随着科技的发展，多自由度系统在许 多领域如航空航天、交通运输、能源等都得到了广泛应用， 因此对多自由度系统振动的研究具有重要意义。
多自由度系统振动与多个学科领域密切相关，如结构力学、流体力学 和声学等，需要加强这些交叉学科领域的应用研究。
多自由度系统振动实验平台的搭建与验证
为了验证多自由度系统振动理论和方法的有效性，需要搭建更加先进 的实验平台，并开展更加系统的实验研究。
谢谢您的聆听
THANKS
被动控制技术
被动控制技术是通过改变系 统的刚度、阻尼和/或质量分 布来减小系统的振动。被动 控制技术不需要外部能源， 而是利用自然现象或物理效 应来减小系统的振动。

第五章 多自由度系统的振动5.1解：用Newton 第二定律或Dalembert 原理分别建立五个质点的动平衡方程1121314413213144131()()()()m xc x c x x c x x k x k x x k x x F ++-+-++-+-= 2272823728232()()m xc x c x x k x k x x F ++-++-= 33431534693832103543153469383210353()()()()()()()()()()m x c x x c x x c c x c x x c x x k x x k x x k k x k x x k x x F +-+-+++-+-+-+-+++-+-=4414341543143415434()()()()m xc x c x x c x x k x k x x k x x F ++-+-++-+-= 55105310535()()m xc x x k x x F +-+-= 整理得1123414334234143341()()m xc c c x c x c x k k k x k x k x F +++--+++--= 2278283782832()()m x c c x c x k k x k x F ++-++-= 3341824568910354105418245689103541053()()m x c x c x c c c c c c x c x c x k x k x k k k k k k x k x k x F --++++++----++++++--=44315335431533544()()m xc x c x c c x k x k x k k x F --++--++= 551031051031055m xc x c x k x k x F -+-+= 写成矩阵形式为MX+CX+KX =F 其中{}T12345F F F F F F = {}T12345X x x x x x =[]12345M diag m m m m m =234437884845689105103535101000000C 0000c c c c c c c c c c c c c c c c c c c c c c c c ++--⎡⎤⎢⎥+-⎢⎥⎢⎥=--+++++--⎢⎥--+⎢⎥⎢⎥-⎣⎦2344378848456891051035351010000000000k k k k k k k k k k k k k k k k k k k k k k k k ++--⎡⎤⎢⎥+-⎢⎥⎢⎥=--+++++--⎢⎥--+⎢⎥⎢⎥-⎣⎦K5.2解：（一）板和地基有四个立柱连接（1）取广义坐标B x 、C x 和D y 质心处的位移为:,,222B c B C B C O O D D x x x x x x lx y y y lθθ+--==+=+= 系统的势能为()222222222222211112222222222222222B C B C D D BCDBCDB C B D C D B C D B C B D C Dx x U kx kx ky k y l l kx kx ky k x x y x x x y x y kx kx ky kx x kx y kx y ⎡⎤-⎛⎫⎛⎫⎛⎫=++++⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦=+++++-+-=++-+-其中, 312EI k l =系统的动能为2222222221112221112222211122222O O B C B C B C D B C B C B C D T mx my J xx x x x x m m y J l xx x x x x m m y J l θ=+++--⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭+--⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 其中, 22211()126J a b ml =+= 拉格朗日函数22222211122222222222B C B C B C D B C D B C B D C Dxx x x x x L T U m m y J l kx kx ky kx x kx y kx y +--⎛⎫⎛⎫⎛⎫=-=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭---+-+当系统发生位移B x 、C x 和D y 时，外力()F t 所做的功为111()()()()()222B C o D D B C x x W F t y F t y l F t y F t x F t x l -⎡⎤=⋅=+=⋅+⋅-⋅⎢⎥⎣⎦因此，等效结点力向量为T11Q ()()()22F t F t F t ⎧⎫=-⎨⎬⎩⎭代入Lagrange 方程d d i i i L LQ t qq ⎛⎫∂∂-= ⎪∂∂⎝⎭ (1,2,,)i n = 得 3332114824241()3622B C D B C D EI EI EI mx mx my x x y F t l l l -++-+= 3331212448241()6322B C D B C D EI EI EI mx mx my x x y F t l l l -+--+-=- 33311242448()22B C D B C D EI EI EI mx mx my x x y F t l l l-++-+= （2）取质心坐标o x 、o y 和θ为广义坐标 系统的势能为2222222211112222222222222222O O O O O O O O l l l l U k x k x k y k y l l l l k x k x k y k y θθθθθθθθ⎡⎤⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=++-+++-⎢⎥⎢⎥⎢⎥⎢⎥⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎛⎫⎛⎫⎛⎫⎛⎫=++-+++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭其中, 312EI k l =系统的动能为222111222O O T mx my J θ=++ ， 其中, 22211()126J a b ml =+= 拉格朗日函数22222221112222222O O O O O O L T U mx my J l l l l k x k x k y k y θθθθθ=-=++⎛⎫⎛⎫⎛⎫⎛⎫-+---+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭当系统发生位移o x 、o y 和θ时，外力()F t 所做的功为: ()o W F t y =⋅ 因此，等效结点力向量为:{}TQ 0()0F t =代入Lagrange d d i i i L LQ t qq ⎛⎫∂∂-= ⎪∂∂⎝⎭ (1,2,,)i n = 方程得 3480O O EImxx l += 348()O O EImyy F t l+= 212406EI ml l θθ+=（3）取质心坐标BD x 、AC y 和θ为广义坐标 系统的势能为2222222211112222221111222222AC AC AC AC BD BD BD BD U kx kx k x k x ky ky k y k y θθθθ⎛⎫⎛⎫=++++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫+++++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭其中, 312EI k l =系统的动能为222111222AC BD T mx my J θ=++ ， 其中, 22211()126J a b ml =+= 拉格朗日函数22222222211122211112222AC BD AC BD AC AC BD BD L T U mx my J kx ky k x k x k y k y θ=-=++--⎛⎫⎛⎫⎛⎫⎛⎫-+---- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭当系统发生位移BD x 、AC y 和θ时，外力()F t 所做的功为()()()AC BD AC BD W F t x y F t x t y ⎤=⋅+=⋅+⋅⎥⎣⎦因此，等效结点力向量为:TQ ()()022F t F t ⎫⎪=⎨⎬⎪⎪⎩⎭代入Lagrange d d i i i L LQ t qq ⎛⎫∂∂-= ⎪∂∂⎝⎭ (1,2,,)i n = 方程得348()AC AC EI mxx F t l +=348()BD BD EI myy F t l += 212406EI ml lθθ+= （二）板和地基有三个立柱连接 （1）取广义坐标B x 、C x 和D y质心处的位移为,,222B c B C B C O O D D x x x x x x lx y y y lθθ+--==+=+= 系统的势能为()22222222222221111222222112222233222222B CB C D D B C D B C D B C B D C D B C D B C B D C Dx x U kx kx ky k y l l kx kx ky k x x y x x x y x y kx kx ky kx x kx y kx y ⎡⎤-⎛⎫⎛⎫⎛⎫=++++⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦=+++++-+-=++-+-其中，312EIk l=。

2. 测量
频率响应函数 力锤或者激振器激励 定义相干函数,自谱等用于验证
3. 曲线拟合
频率 阻尼 留数 (模态振型)
4. 验证
MAC (模态置信准则) 模态置信因子 相位分布 模态参与因子 ........
BA 7679-16, 15
频率响应函数
[m/s瞉 80 40 0 -40 -80 0 40m 80m 120m [s] 160m 200m 240m Time(Response) - Input Working : Input : Input : FFT Analyzer
设置和测量 显示器上的几何模型指导传感 器的安装 参量参数的图形化设置 测量状态的声音和视觉通知 自动的标签DOF – 当测量时可以标签 双击探测….
屏幕上的几何模型 安装传感器
时间计权
过载指示
BA 7679-16, 27
智能型传感器使得设置极其方便
内置的TEDS（ 读/写 传感器电子数据表 ） 芯片,
故障诊断
– 降低过大的振动水平 – 确保共振远离激励频率
仿真“假如。则。。”
– 确定载荷 – 复杂激励下结构的响应 – 结构动力学修改
结构综合分析
– 预测组装子部件或总成的动力学行为
模态测试
首先利用在飞机工业 今天也广泛的应用于汽车工业和许多其他工业
BA 7679-16, 11
故障诊断
频率响应函数
模态分析
BA 7679-16, 1
引言 2
当今需求： 运行的速度越来越快 对燃油经济性要求越来越高 结构越来越轻量化 这些需求要求降低结构重量 结果： 结构变得越来越“弱” 共振频率向激励频率范围内移动 由于动态载荷的存在，结构将更容易“失效”

x1 A1(1) sin p1t 1
(1) x2 A2 sin p1t 1 (1) xn An sin p1t 1
每个坐标均以同一圆频率p1及同一相位角 1作简谐振动，称为 系统第一阶主振动。
1 类似的，当系统在某些特殊的初始条件下，还可以产生系统的 第二阶、第三阶、…一直到第n阶主振动，具有与第一阶主振动 完全类似的性质。




2 2 2 m p A k m p A k m p 21 21 j 1 22 22 j 2 2 n 1 2 n 1 j An 1




k1n m1n p 2 j An k 2 n m2 n p 2 j An






y1 11 P 1 m1 y1 12 P 2 m2 y 2 1n P n mn y n y2 21 P 1 m1 y1 22 P 2 m2 y 2 2 n P n mn yn yn n1 P 1 m1 y1 n 2 P 2 m2 y2 nn P n mn y n
化简后得
1 K1 K 2 x1 K 2 x2 P m1 x 1 2 K 2 x1 K 2 K 3 x2 K 3 x3 P2 m2 x 3 K 3 x2 K 3 x3 P3 m3 x
此式可用矩阵形式表达式
K x P M x
11 12 1n 2n 21 22 , n1 n 2 nn
m1 0 0 m 2 M 0 0
0 0 mn

模态分析
定义
图解
是一种坐标变换。目的在于把原在物理坐标系统中描述的响应向 量，放到所谓“模态坐标系统”中来描述。运用这一坐标的好处是：利用各特征向量之间的正交特性，可使描述响应向量的各个坐标互相独立而无耦合。换句话讲，在这一坐标系统中，振动方程是一组互无耦合的方程，每一个坐标均可单独求解。
实验梁的力锤敲击信号：
(5）数据预处理 调节采样数据 采样完成后，对采样数据重新检查并再次回放计算频响函数数据。一通道的力信号加力窗，在力窗窗宽调整合适。对响应信号加指数窗。设置完成后，回放数据重新计算频响函数数据。
力信号加力窗
响应信号加指数窗
启动回放
（6）模态分析 l 几何建模：自动创建矩形模型，输入模型的长宽参数以及分段数；打开结点信息窗口，编写测点号；
DHMA模态软件分析方法及应用领域
应用
大型建筑物：
大型桥梁：
DHMA模态分析软件功能
几何建模 读入CAD平面图形、ANSYS有限元模型文件；可以直接在界面上完成部件、结点、连线的填加、删除、移动、复制、粘贴以及参数修改等；可自动生成规则模型；为了更接近实际结构，测点之间可插入非测量结点，软件自动根据周围测点数据编写非测点的约束方程。对模型可以进行平移、旋转、放大缩小、线条颜色修改、背景颜色修改、四视图单独或同时显示；
（2）仪器连接 仪器连接如下图所示，其中力锤上的力传感器接动态采集分析仪的第一通道，DH201加速度传感器接第二通道。
（3）打开仪器电源，启动DHDAS控制分析软件， 选择分析/频响函数分析功能。
实验梁平面图
在菜单“ 分析(N) ”选择分析模式“单输入频响”。 在新建的四个窗口内，分别单击右键，在“信号选择”对话框中设定四个窗口依次为：频响函数数据、1-1通道的时间波形、相干函数数据和1-2通道的时间波形,如下图。

2022/2/12 《振动力学》
代入，得： (FM I)φ 0 特征方程： FMI 0 18
多自由度系统振动 / 多自由度系统的自由振动/模态
• 多自由度系统的模态（主振型）
正定系统： M X KX 0
主振动： X φ asi nt ()
XRn M、 KRnn
0 φRn
特征值问题： (K2M)φ0
7
《振动力学》
多自由度系统振动 / 多自由度系统的自由振动
• 多自由度系统的固有频率
作用力方程： MXKXP(t) XRn
自由振动方程： MXKX0
和单自由度系统一样，自 由振动时系统将以固有频 率为振动频率。
在考虑系统的固有振动时，最感兴趣的是系统的同 步振动，即系统在各个坐标上除了运动幅值不相同外， 随时间变化的规律都相同的运动 。
则有：(TTAT)T＝TTAT(TT)T＝TTAT 正定性质：若原来的刚度矩阵K 正定，则（TTKT）仍正定。
因此坐标变换X ＝TY 不改变系统的正定性质。 对于质量矩阵也如此。
2022/2/12
5
《振动力学》
回顾：单自由度系统自由振动－无阻尼自由振动
小结：
单自由度系统自由振动分析的一般过程：
1、由工程装置建立自由振动的一般方程，并写出振动的标准方程； 2、根据标准方程，建立本征方程并计算得到本征值； 3、根据本征值，写出标准方程的通解； 4、根据初始条件，计算标准方程的特解。
f(t)asint(), 0
f(t)a tb,
0
主振动
（1）正定系统 0
只可能出现形如 X φ asi nt ()的同步运动。
系统在各个坐标上都是按相同频率及初相位作简谐振动。
（2）半正定系统 0

振动分析师培训课件Contents目录•振动分析概述•振动分析基础知识•振动分析技术•振动分析案例•振动分析软件与工具•振动分析师的职业发展与认证01定义高效的运行。

目的振动分析的定义和目的振动信号的测量振动信号的分析振动模型的建立振动预测和控制01020304通过传感器测量振动信号，如加速度、速度和位移等。

对测量得到的振动信号进行分析，包括时域分析和频域分析。

根据实际系统的结构和动力学特性，建立振动模型，如线性模型和非线性模型。

基于建立的模型和实际测量得到的信号，预测和控制系统的振动性能。

02振动系统的分类线性系统是指其输出响应与输入激励成正比的系统，如弹簧-质量-阻尼器系统。

非线性系统是指其输出响应与输入激励不成正比的系统，如摩擦力、磁滞等。

时变系统是指系统的参数随时间变化的系统，如受温度影响的弹性模量。

随机系统是指其输出响应具有随机性质的系统，如地震、海浪等。

线性系统非线性系统时变系统随机系统时域分析频域分析时频分析特征提取振动信号的描述和分析方法时频分析是同时考虑时间和频率特性的分析方法，如短时傅里叶变换、小波变换等。

特征提取是从振动信号中提取出能够反映系统特性的参数或指标的方法，如频率、幅值、相位等。

传感器数据采集器是用来采集和记录振动信号的设备，如示波器、数据采集卡等。

数据采集器激振器抗干扰技术是用来减小测量误差和干扰的影响，如信号调理、滤波等。

抗干扰技术振动测试设备与测量技术03通过时域波形图，可以观察到振动信号随时间的变化情况，了解振动的幅值和趋势。

时域波形图峰值检测平均值计算峰值检测是时域分析中的重要手段，通过检测信号中的峰值，可以了解振动信号的最大值和最小值。

平均值计算是评估振动信号总体“平均”水平的重要方法，通常用于评估设备的平均运行状态。

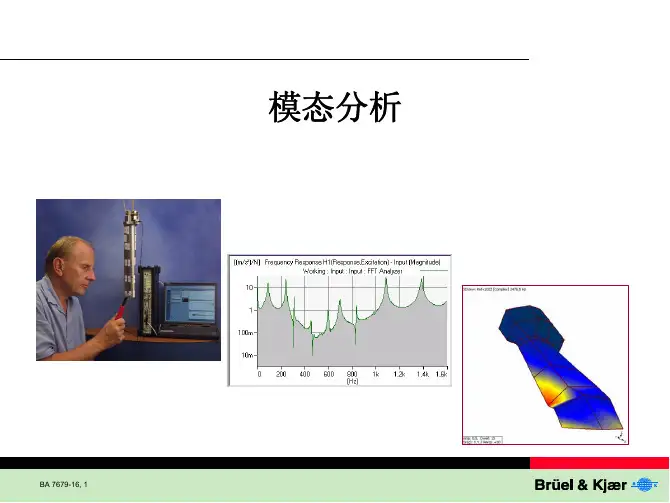
030201频谱分析障和异常。

频谱图频率成分的信号。

滤波器设计模态振型通过模态分析，可以识别出结构的模态类型和模态参数，为结构的动态特性和稳定性分析提供依据。

第五章 结构的强迫振动响应分析§5.1 概述如果结构已经用有限元方法进行了离散化，当一个结构系统受到外激励作用时，其响应就是一个多自由度系统的强迫振动问题的解。

求解多自由度系统强迫振动响应的方法之一就是直接积分法。

考虑到实际结构的高维数（自由度数很大）而给求解带来的困难，往往在实际求解中采用模态叠加法。

直接积分法和模态叠加法这两种方法都可以得到具有相当精度的振动响应解，并且各有其特点。

§5.2 求解强迫振动响应的直接积分法对动力学基本方程)}({}]{[}]{[}]{[t P U K U C UM =++ （5－1）进行直接积分，其含义是指在对方程进行积分之前，不对其进行任何形式的变换，在积分中，实际上是按时间步长逐步积分的。

这样做的实质是基于如下考虑：（1） 只在相隔t ∆的一些离散时间区间上、而不是在整个时间区间上的任一个时刻t 上满足方程，即平衡是在求解区间上的一些离散时刻上获得的。

（2） 假定位移、速度、加速度在每一个时间区间t ∆内按一定规律变化，也正是采用不同的变化形式，决定了各种直接积分解的精度、稳定性和求解速度。

首先，设}{}{}{000U U U 表示初始时刻（0=t ）的位移、速度和加速度为已知向量，要求出从0=t 到T t =的解，则把时间段T 均分为n 个间隔n T t /=∆，所用的积分是在T t t ,2,∆∆上求方程的近似解。

即要在t t t ,2,∆∆的解已知的情况下，求解t t ∆+时刻的解。

【中心差分法】若基本方程式的平衡关系作为一个常系数微分方程组，则可以用任一种差分格式通过位移来表示速度和加速度。

通常采用中心差分格式，这是一个行之有效的求解微分方程的格式。

}){}({21}{}){}{2}({1}{2t t t t tt t t t t t U U tU U U U tU ∆∆∆∆∆∆-++--=+-= （5－2）假定}{t U 及前一时刻的位移}{t t U ∆-已经求得，则将}{t U }{tU 代入方程（5－1）得到：}]){[21][1(}]){[2]([}{}]){[21][1(222t t t t t t U C tM tU M tK P U C tM t∆∆∆∆∆∆∆-+----=+（5－3）由此式求出}{t t U ∆+上述格式是一个显式格式。