SVM支持向量机算法的详细推导 详细到每个步骤 值得
- 格式:pdf
- 大小:1.20 MB
- 文档页数:44

svm算法公式摘要:1.简介2.SVM 算法基本思想3.SVM 算法公式推导4.SVM 算法应用场景与优缺点5.总结正文:1.简介支持向量机(Support Vector Machine,SVM)是一种经典的二分类机器学习算法。
它通过划分超平面,使得不同类别的数据点到超平面的距离最大,从而实现分类。
SVM 算法具有良好的泛化能力,广泛应用于文本分类、图像分类、生物信息学等领域。
2.SVM 算法基本思想SVM 算法的基本思想是找到一个最佳超平面,使得两个类别之间的距离(即几何间隔)最大化。
为了找到这个最佳超平面,SVM 算法需要解决一个优化问题,即求解一个凸二次规划问题。
3.SVM 算法公式推导设训练样本集为X = {x1, x2, ..., xn},标签为Y = {y1, y2, ..., yn},其中yi∈{-1, 1}。
SVM 算法的优化目标是最小化误分类点到超平面的几何间隔之和,即:min ∑(yi - ∑αi * yi * kernel(xi, xj))^2其中,αi 表示第i 个支持向量对应的拉格朗日乘子,kernel(xi, xj) 表示核函数,用于计算两个向量之间的相似度。
对于线性核函数,kernel(xi, xj) = xi·xj;对于多项式核函数,kernel(xi, xj) = (xi·xj + 1)^d。
4.SVM 算法应用场景与优缺点SVM 算法在以下场景中表现良好:- 数据集具有较高维度,但线性可分;- 数据集中存在噪声或异常值;- 需要对类别进行细分的场景。
SVM 算法的优点包括:- 具有较好的泛化能力,能有效处理过拟合问题;- 对于线性可分数据集,能够实现最优分类效果;- 支持多种核函数,可处理非线性问题。
SVM 算法的缺点包括:- 对于非线性数据集,需要选择合适的核函数,否则可能无法获得好的分类效果;- 计算复杂度较高,尤其是当数据量较大时。
5.总结支持向量机(SVM)是一种经典的二分类机器学习算法,通过寻找最佳超平面来实现分类。

svm算法公式SVM算法公式支持向量机(Support Vector Machine,简称SVM)是一种常用的机器学习算法,被广泛应用于分类和回归问题的解决中。
它的核心思想是通过找到一个最优超平面来划分不同类别的数据点,从而实现分类的目标。
SVM算法的公式可以用如下方式表达:1. 数据准备假设我们有一个包含N个样本的训练集D={(x1, y1), (x2, y2), ... , (xN, yN)},其中xi表示第i个样本的特征向量,yi表示第i个样本的类别标签。
特征向量xi具有n个维度,即xi=(x1i, x2i, ... , xni)。
2. 寻找最优超平面SVM的目标是找到一个最优超平面,使得该超平面能够最大化样本点到该超平面的间隔,并且能够正确地将不同类别的样本点分开。
最优超平面可以用如下公式表示:w·x + b = 0其中,w表示超平面的法向量,b表示超平面的截距。
w·x表示w 和x的内积。
根据这个公式,我们可以将样本点分为两类:w·x + b > 0的样本点属于一类,w·x + b < 0的样本点属于另一类。
3. 线性可分情况如果训练集D是线性可分的,即存在一个超平面完全能够将两类样本点分开,那么我们可以通过一个优化问题来求解最优超平面。
优化问题可以用如下公式表示:min 1/2 ||w||^2s.t. yi(w·xi + b) ≥ 1, i=1,2,...,N其中,||w||表示向量w的范数,yi表示第i个样本点的类别标签。
这个优化问题的目标是最小化w的范数,同时满足所有样本点的分类约束条件。
4. 线性不可分情况如果训练集D不是线性可分的,那么我们可以通过引入松弛变量(xi, ξi)来解决这个问题。
松弛变量可以将样本点分类约束条件放宽,使得一些样本点可以位于超平面的错误一侧。
此时,优化问题可以用如下公式表示:min 1/2 ||w||^2 + C Σξis.t. yi(w·xi + b) ≥ 1 - ξi, i=1,2,...,Nξi ≥ 0, i=1,2,...,N其中,C是一个正则化参数,用来平衡最小化w的范数和最小化松弛变量的重要性。

SVM算法详解范文SVM(支持向量机)是一种常用的监督学习算法,广泛应用于分类和回归问题。
它的基本思想是找到一个最优的超平面,能够将不同类别的样本点分开。
支持向量机具有较好的泛化能力和鲁棒性,在实际应用中取得了很好的效果。
一、SVM的基本原理1.线性可分情况下当训练样本线性可分时,SVM算法的目标是找到一个能够将正负样本完全分开的超平面。
这个超平面的选择是使得所有样本点到超平面的距离最大化,即最大化间隔。
2.线性不可分情况下当样本线性不可分时,SVM使用核函数将样本映射到高维特征空间中,使得样本可以在高维空间线性可分。
常用的核函数有线性核函数、多项式核函数和高斯核函数等。
二、SVM的数学模型SVM的数学模型可以表示为一个凸二次规划问题,即:min 1/2 ∥w∥²s.t. yi(w·xi+b)≥1 , i=1,2,...,n其中w是超平面的法向量,b是超平面的截距,(xi,yi)是训练样本点,n是样本总数。
这个问题可以通过拉格朗日函数和KKT条件等方法求解。
三、SVM的优缺点SVM具有以下优点:1.SVM能够处理高维特征空间中的分类问题。
2.SVM对于小样本数据集效果较好。
3.SVM能够处理非线性问题,通过核函数将样本映射到高维特征空间。
SVM的缺点包括:1.SVM对于大规模样本集需要较长的训练时间。
2.SVM对于噪声和缺失数据敏感。
3.SVM模型的选择和核函数的选取对结果有较大影响。
四、SVM算法的步骤1.数据预处理:对数据进行标准化和归一化处理。
2.选择核函数:根据问题的特点选择合适的核函数。
3.参数选择:确定正则化项参数和核函数的参数。
4.求解凸二次规划问题:通过优化算法求解凸二次规划问题。
5.模型评估:通过交叉验证等方法评估模型的性能。
6.预测与分类:使用训练好的SVM模型进行预测和分类。
五、SVM的改进和拓展1.核函数选择:根据问题需求和数据特点选择合适的核函数。
2.超参数调优:使用交叉验证等方法调优SVM模型的超参数。

支持向量机算法的原理和应用支持向量机(Support Vector Machine, SVM)是一种基于统计学习理论的机器学习算法,它可以在数据集中找到一个最优超平面,将不同类别的样本分割开来。
在分类问题中,SVM通过构建一个超平面来对不同类别的样本进行分类;在回归问题中,SVM可以用来拟合非线性关系的数据。
SVM的核心思想是最大化间隔,即找到一个能够将不同类别的样本分隔开的超平面,使得两侧最近的样本点到超平面的距离最大。
这些最近的样本点被称为支持向量,它们决定了最终划分超平面的位置。
SVM的基本原理可以分为以下几个步骤:1.数据准备:首先需要对数据进行预处理,包括数据清洗、归一化、特征提取等。
2.特征选择:选择与分类问题相关的特征。
3.模型构建:构建SVM模型,选择适当的核函数、设置参数。
4.模型训练:使用已标记的训练样本进行模型训练,找到最佳的超平面。
5.模型预测:用训练好的模型对新样本进行预测,即将新样本进行分类。
SVM算法的应用非常广泛,主要包括以下几个方面:1.二分类问题:SVM在二分类问题中表现出色,特别适用于具有较大类别间距离且样本数目较少的情况。
例如,在垃圾邮件分类中,SVM可以将垃圾邮件和正常邮件进行有效地区分。
2.多分类问题:通过将多个二分类器组合起来,SVM可以用于解决多分类问题。
例如,在手写数字识别中,可以使用SVM对不同的数字进行分类。
3.异常检测:SVM可以用于异常检测,通过将异常样本与正常样本分开。
例如,在网络入侵检测中,SVM可以帮助识别潜在的入侵行为。
4.文本分类:SVM在文本分类问题中也有广泛的应用。
例如,在垃圾短信识别中,可以使用SVM对短信进行分类。
5.图像识别:SVM在图像识别问题中有很好的表现。
例如,在人脸识别中,可以使用SVM对不同人脸进行分类。
除了以上几个应用领域,SVM还可以应用于生物信息学、计算机视觉、自然语言处理等问题的解决。
尽管SVM算法在许多问题中都表现出色,但也存在一些限制。

机器学习--⽀持向量机(SVM)算法的原理及优缺点⼀、⽀持向量机(SVM)算法的原理 ⽀持向量机(Support Vector Machine,常简称为SVM)是⼀种监督式学习的⽅法,可⼴泛地应⽤于统计分类以及回归分析。
它是将向量映射到⼀个更⾼维的空间⾥,在这个空间⾥建⽴有⼀个最⼤间隔超平⾯。
在分开数据的超平⾯的两边建有两个互相平⾏的超平⾯,分隔超平⾯使两个平⾏超平⾯的距离最⼤化。
假定平⾏超平⾯间的距离或差距越⼤,分类器的总误差越⼩。
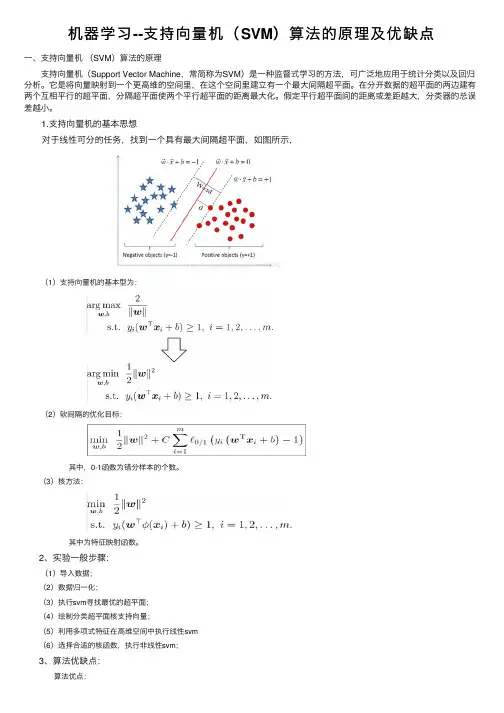
1.⽀持向量机的基本思想 对于线性可分的任务,找到⼀个具有最⼤间隔超平⾯,如图所⽰, (1)⽀持向量机的基本型为: (2)软间隔的优化⽬标: 其中,0-1函数为错分样本的个数。
(3)核⽅法: 其中为特征映射函数。
2、实验⼀般步骤: (1)导⼊数据; (2)数据归⼀化; (3)执⾏svm寻找最优的超平⾯; (4)绘制分类超平⾯核⽀持向量; (5)利⽤多项式特征在⾼维空间中执⾏线性svm (6)选择合适的核函数,执⾏⾮线性svm; 3、算法优缺点: 算法优点: (1)使⽤核函数可以向⾼维空间进⾏映射 (2)使⽤核函数可以解决⾮线性的分类 (3)分类思想很简单,就是将样本与决策⾯的间隔最⼤化 (4)分类效果较好 算法缺点: (1)SVM算法对⼤规模训练样本难以实施 (2)⽤SVM解决多分类问题存在困难 (3)对缺失数据敏感,对参数和核函数的选择敏感 ⼆、数学推导过程 对于线性可分的⽀持向量机求解问题实际上可转化为⼀个带约束条件的最优化求解问题: 推理过程: 结果: 对于线性不可分的⽀持向量机求解问题实际上可转化为⼀个带约束条件的soft-margin最优化求解问题:三、代码实现1、线性svmimport numpy as npfrom sklearn.datasets import load_irisimport matplotlib.pyplot as pltfrom sklearn.preprocessing import StandardScalerfrom sklearn.svm import LinearSVCfrom matplotlib.colors import ListedColormapimport warningsdef plot_decision_boundary(model,axis):x0,x1=np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))x_new=np.c_[x0.ravel(),x1.ravel()]y_predict=model.predict(x_new)zz=y_predict.reshape(x0.shape)custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)w = model.coef_[0]b = model.intercept_[0]plot_x = np.linspace(axis[0],axis[1],200)up_y = -w[0]/w[1]*plot_x - b/w[1] + 1/w[1]down_y = -w[0]/w[1]*plot_x - b/w[1] - 1/w[1]up_index = (up_y>=axis[2]) & (up_y<=axis[3])down_index = (down_y>=axis[2]) & (down_y<=axis[3])plt.plot(plot_x[up_index],up_y[up_index],c='black')plt.plot(plot_x[down_index],down_y[down_index],c='black')warnings.filterwarnings("ignore")data = load_iris()x = data.datay = data.targetx = x[y<2,:2]y = y[y<2]scaler = StandardScaler()scaler.fit(x)x = scaler.transform(x)svc = LinearSVC(C=1e9)svc.fit(x,y)plot_decision_boundary(svc,axis=[-3,3,-3,3])plt.scatter(x[y==0,0],x[y==0,1],c='r')plt.scatter(x[y==1,0],x[y==1,1],c='b')plt.show()输出结果:2、⾮线性-多项式特征import numpy as npfrom sklearn import datasetsimport matplotlib.pyplot as pltfrom sklearn.preprocessing import PolynomialFeatures,StandardScaler from sklearn.svm import LinearSVCfrom sklearn.pipeline import Pipelinefrom matplotlib.colors import ListedColormapimport warningsdef plot_decision_boundary(model,axis):x0,x1=np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1), np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1) )x_new=np.c_[x0.ravel(),x1.ravel()]y_predict=model.predict(x_new)zz=y_predict.reshape(x0.shape)custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9']) plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)def PolynomialSVC(degree,C=1.0):return Pipeline([('poly',PolynomialFeatures(degree=degree)),('std_scaler',StandardScaler()),('linearSVC',LinearSVC(C=1e9))])warnings.filterwarnings("ignore")poly_svc = PolynomialSVC(degree=3)X,y = datasets.make_moons(noise=0.15,random_state=666)poly_svc.fit(X,y)plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])plt.scatter(X[y==0,0],X[y==0,1],c='red')plt.scatter(X[y==1,0],X[y==1,1],c='blue')plt.show()输出结果:3、⾮线性-核⽅法from sklearn.preprocessing import StandardScalerfrom sklearn.svm import SVCfrom sklearn.pipeline import Pipelinefrom sklearn import datasetsfrom matplotlib.colors import ListedColormapimport numpy as npimport matplotlib.pyplot as pltimport warningsdef plot_decision_boundary(model,axis):x0,x1=np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1), np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1) )x_new=np.c_[x0.ravel(),x1.ravel()]y_predict=model.predict(x_new)zz=y_predict.reshape(x0.shape)custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9']) plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)def RBFKernelSVC(gamma=1.0):return Pipeline([('std_scaler',StandardScaler()),('svc',SVC(kernel='rbf',gamma=gamma))])warnings.filterwarnings("ignore")X,y = datasets.make_moons(noise=0.15,random_state=666)svc = RBFKernelSVC(gamma=100)svc.fit(X,y)plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])plt.scatter(X[y==0,0],X[y==0,1],c='red')plt.scatter(X[y==1,0],X[y==1,1],c='blue')plt.show()输出结果:。

超详细SVM(支持向量机)知识点一. 简单概括一下SVM:SVM 是一种二类分类模型。
它的基本思想是在特征空间中寻找间隔最大的分离超平面使数据得到高效的二分类,具体来讲,有三种情况(不加核函数的话就是个线性模型,加了之后才会升级为一个非线性模型):•当训练样本线性可分时,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机;•当训练数据近似线性可分时,引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机;•当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
二. SVM 为什么采用间隔最大化(与感知机的区别):当训练数据线性可分时,存在无穷个分离超平面可以将两类数据正确分开。
感知机利用误分类最小策略,求得分离超平面,不过此时的解有无穷多个。
线性可分支持向量机利用间隔最大化求得最优分离超平面,这时,解是唯一的。
另一方面,此时的分隔超平面所产生的分类结果是最鲁棒的,对未知实例的泛化能力最强。
三. SVM的目标(硬间隔):有两个目标:第一个是使间隔最大化,第二个是使样本正确分类,由此推出目标函数:稍微解释一下,w是超平面参数,目标一是从点到面的距离公式化简来的,具体不展开,目标二就相当于感知机,只是把大于等于0进行缩放变成了大于等于1,为了后面的推导方便。
有了两个目标,写在一起,就变成了svm的终极目标:四. 求解目标(硬间隔):从上面的公式看出,这是一个有约束条件的最优化问题,用拉格朗日函数来解决。
上式的拉格朗日函数为:在满足Slater定理的时候,且过程满足KKT条件的时候,原问题转换成对偶问题:先求内部最小值,对和 b 求偏导数=0可得将其带入到上式中可以得到此时需要求解α ,利用SMO(序列最小优化)算法:五. 软间隔:不管直接在原特征空间,还是在映射的高维空间,我们都假设样本是线性可分的。
虽然理论上我们总能找到一个高维映射使数据线性可分,但在实际任务中,寻找一个合适的核函数核很困难。

svm算法公式【原创版】目录1.SVM 算法概述2.SVM 算法公式简介3.SVM 算法公式详解4.SVM 算法公式的应用5.总结正文一、SVM 算法概述支持向量机(Support Vector Machine,SVM)是一种经典的二分类机器学习算法,由 Corinna Cortes 和 Vladimir Vapnik 于 1995 年提出。
它的主要思想是找到一个最佳超平面,使得不同类别的数据点之间的距离最大化。
SVM 算法在实际应用中表现出卓越的性能,被广泛应用于模式识别、图像识别、文本分类等领域。
二、SVM 算法公式简介SVM 算法的核心是基于最大间隔分隔超平面,其公式可以表示为:1.找到一个超平面 $w * x + b = 0$,使得所有样本点到这个超平面的几何距离最大化。
2.通过对所有样本点进行分类,得到分类结果。
三、SVM 算法公式详解SVM 算法的公式可以分为以下三个部分:1.最大间隔超平面假设我们有一组样本点 $(x_1, y_1), (x_2, y_2),..., (x_n, y_n)$,其中 $y_i in {-1, 1}$ 表示样本点属于正负两个类别。
我们的目标是找到一个超平面 $w * x + b = 0$,使得所有样本点到这个超平面的几何距离最大化。
我们可以通过拉格朗日乘子法(Lagrange Multiplier)来解决这个问题。
2.拉格朗日乘子法拉格朗日乘子法是一种用于求解带约束优化问题的方法。
在 SVM 算法中,我们希望在满足约束条件的前提下,最大化超平面的几何距离。
我们可以引入拉格朗日乘子 $alpha_i$,将问题转化为求解无约束问题的最大化问题。
3.软间隔和硬间隔根据拉格朗日乘子法的求解结果,我们可以得到两种类型的超平面:软间隔超平面和硬间隔超平面。
- 软间隔超平面:当某些样本点不满足约束条件时,我们称之为软间隔超平面。
在这种情况下,我们可以继续调整超平面,使得更多的样本点满足约束条件。

支持向量机的工作原理支持向量机,简称SVM,是一种基于统计学习理论的有监督学习算法。
SVM在许多领域都被广泛应用,如数据挖掘、机器视觉、自然语言处理等领域。
SVM的工作原理可以概括为以下几个步骤:1. 数据预处理在SVM算法中,首先需要对数据进行预处理,也叫做特征提取。
这个过程中需要将原始数据转换为可供算法处理的特征向量。
2. 建立模型在SVM算法中,需要建立一个目标函数,该函数能够将数据划分成正类和负类。
目标函数的定义通常是最优化问题的形式,根据数据的不同,有时候目标函数比较难以求解,会取得近似解。
3. 优化模型SVM算法中需要对目标函数进行优化,以找到最优解。
由于SVM算法是一种凸优化问题,可以使用一些优化方法,如拉格朗日乘子法和序列最小优化算法等。
在实际模型优化过程中,如果数据太大,模型的优化会非常耗时,甚至得不到结果。
4. 选择最佳超参数SVM算法中有两个超参数,即kernel函数和正则化参数C。
kernel函数用于将特征空间映射到高维空间,而正则化参数C是用来控制模型的复杂度的。
在实践中,通常使用交叉验证来确定最佳的超参数,交叉验证可以帮助选择最优的超参数。
5. 预测在SVM算法中,可以使用训练数据集训练出最佳SVM模型,再使用测试数据集对模型进行测试和评价。
对于新的数据,可以使用训练好的模型对其进行分类。
在预测过程中,可以计算每一个数据点到分界线的距离(即一个样本点和支持向量之间的距离),使用这个距离来进行预测。
以上就是SVM算法的基本工作原理,通过对数据的预处理、建立模型、优化模型、选择最佳超参数和预测等几个步骤,SVM算法可以在很多领域中实现有效的分类和回归。

支持向量机推导支持向量机(Support Vector Machine,SVM)是一种常用的机器学习算法,它可以用于分类和回归问题。
SVM的核心思想是找到一个最优的超平面,将不同类别的数据分开。
本文将从数学角度推导SVM的基本原理。
我们需要了解什么是超平面。
在二维空间中,超平面就是一条直线,可以将数据分成两类。
在三维空间中,超平面就是一个平面,可以将数据分成两类。
在高维空间中,超平面就是一个超平面,可以将数据分成两类。
SVM的目标就是找到一个最优的超平面,使得不同类别的数据点距离超平面最远。
假设我们有一个二分类问题,数据集为{(x1,y1),(x2,y2),...,(xn,yn)},其中xi是一个n维向量,yi∈{-1,1}表示数据点的类别。
我们的目标是找到一个超平面w·x+b=0,使得对于所有的i,有yi(w·xi+b)≥1。
为了找到最优的超平面,我们需要最大化间隔(margin),即数据点到超平面的距离。
假设超平面的法向量为w,那么数据点xi到超平面的距离为|w·xi+b|/||w||,其中||w||表示w的模长。
我们的目标是最大化间隔,即最大化||w||,同时满足约束条件yi(w·xi+b)≥1。
这是一个带约束的优化问题,可以使用拉格朗日乘子法来求解。
我们定义拉格朗日函数L(w,b,α)为:L(w,b,α)=1/2||w||^2-∑αi[yi(w·xi+b)-1]其中αi是拉格朗日乘子,用于表示约束条件。
我们的目标是最大化L(w,b,α),即最大化||w||,同时满足约束条件yi(w·xi+b)≥1。
对于任意的αi>0,都有yi(w·xi+b)-1=0,即数据点xi在超平面上。
对于αi=0,数据点xi不在超平面上。
我们可以通过求解拉格朗日对偶问题来求解原始问题。
拉格朗日对偶问题是将原始问题转化为一个只包含拉格朗日乘子的问题。

⽀持向量机-SVM推导(C语⾔源码)很久之前就想把SVM系统的解析⼀下,争取把西⽠书的这⼀部分顺⼀遍,并⽤C语⾔对各个部分进⾏解析,加深理解。
基本概念给定训练样本集D=(Xl,Yl),(X2,Y2),...,(Xm,Ym), \(Yi ε{-1, 1)\),分类学习最基本的想法就是基于训练、集D 在样本空间中找到⼀个划分超平⾯、将不同类别的样本分开。
在样本空间中,划分超平⾯可通过如下线性⽅程来描述:其中,w=(w1;w2,...,ωd)?决定了超平⾯的⽅向; b 为位移项,决定了超平⾯与原点之间的距离.显然,划分超平⾯可被法向量ω和位移b 确定,下⾯我们将其记为(矶的.样本主R 间中任意点2 到超平⾯(矶的的距离可写为:r=|w T x+b|||ω||(6.2)间隔与⽀持向量间隔:,两个异类⽀持向量到超平⾯的距离之和,即γ=2ω⽀持向量:距离超平⾯最近的这⼏个训练样本点使式(6.3) 的等号成⽴,SVM的基本型对偶问题那么?如何求解式(6.11) 呢?不难发现j 这是⼀个三次规划问题?可使⽤通⽤的⼆次规划算法来求解;然⽽?该问题的规模正⽐于训练样本数7 这会在实际任务中造成很⼤的开销.为了避开这个障碍,⼈们通过利⽤问题本⾝的特性,提出了很多⾼效算法, SMO (Sequential Minimal Optimization) 是其中⼀个著名的代表[Platt , 1998].SMO算法SMO的基本思路是先固定向之外的所有参数,然后求向上的极值.由于存在约束艺汇1 叫ντ⼯0 ,若固定向之外的其他变量?则αz 可由其他变量导出.于是, SMO 每次选择两个变量问和町,并固定其他参数.这样,在参数初始化后, SMO 不断执⾏如下两个步骤直⾄收敛:1. 选取⼀对需更新的变量αi和αj;2. 固定αi和αj以外的参数,求解式(6.11)获得更新后的叫αi和αj.注意到只需选取的问丰IJα3 中有⼀个不满⾜KKT 条件(6.13) ,⽬标函数就会在选代后减⼩[Osuna et al., 1997]. 直观来看, KKT 条件违背的程度越⼤?则变量更新后可能导致的⽬标函数值减幅越⼤.于是, SMO 先选取违背KKT 条件程度最⼤的变量.第⼆个变量应选择⼀个使⽬标函数值减⼩最快的变量,但由于⽐较各变量所对应的⽬标函数值减幅的复杂度过⾼,因此SMO 采⽤了⼀个启发式:使选取的两变量所对应样本之间的问隔最⼤. 种直观的解释是,这样的两个变量有很⼤的差别,与对两个相似的变量进⾏更新相⽐,对它们进⾏更新会带给⽬标函数值更⼤的变化.核函数对于线性不可分的训练样本,可将样本从原始空间映射到⼀个更⾼维的特征空间,使得样本在这个特征空间内线性可分.核函数定理常⽤的核函数Processing math: 100%。
svm的推导过程哎呀,咱今天就来说说 SVM 的推导过程,这可真是个有趣的玩意儿呢!你想啊,SVM 就像是一个超级聪明的小侦探,要在一大堆数据里找出最关键的线索。
它的目标就是找到那条能把不同类别数据分得最清楚的线或者面。
一开始呢,我们有好多好多的数据点,就像一群调皮的小精灵在那蹦跶。
SVM 这个小侦探就得想办法让它们各归各位。
它是怎么做到的呢?它会找一个最优的决策边界,这个边界就像是一道坚固的城墙,把不同类别的数据隔开。
那怎么找这个最优边界呢?这可就有讲究啦!就好比你要把一群红球和一群蓝球分开,你得找个最合适的位置划线,让红球都在一边,蓝球都在另一边,而且这条线还得离两边的球都尽可能远。
这时候就要用到一些数学魔法啦!我们要计算一些距离啊,优化一些参数啊。
这就像是在给小侦探装备各种厉害的工具,让它能更准确地完成任务。
比如说,我们要考虑那些离决策边界很近的点,这些点可重要啦,就像战场上的关键据点。
我们得特别关注它们,让它们来帮我们确定最优的边界。
然后呢,经过一番折腾,小侦探 SVM 终于找到了那条完美的决策边界!哇塞,是不是很厉害?你说这过程难不难?当然难啦!但这就是挑战的乐趣所在嘛。
就像爬山一样,虽然过程很累,但当你爬到山顶,看到那美丽的风景,一切都值啦!SVM 的推导过程可不只是一堆枯燥的数学公式,它里面蕴含着智慧和巧妙。
每一步都像是解开一个谜题,让人充满了好奇和探索的欲望。
而且哦,学会了 SVM 的推导过程,你就像是掌握了一门神奇的武功秘籍,可以在数据的江湖里大展身手啦!你可以用它来解决各种各样的问题,让那些数据都乖乖听话。
所以啊,别害怕这个推导过程,勇敢地去探索吧!说不定你会发现其中的无限乐趣呢!怎么样,是不是已经迫不及待想去研究研究啦?加油吧!。
支持向量机算法原理与应用支持向量机算法(Support Vector Machine, SVM)是机器学习领域中一种非常重要的算法。
SVM的原理和应用十分广泛,不仅被用于分类问题,还被用于回归、异常检测等方面。
本文将介绍SVM的原理和应用,并对它的一些变体进行讨论。
1. SVM的原理SVM的基本思想是通过寻找一个最优的超平面,将不同类别的数据分开。
这个最优的超平面是使得不同类别之间的间隔最大的超平面。
在二分类问题中,可以表示为:$$\boldsymbol{w} \cdot \boldsymbol{x} + b = 0$$其中,$\boldsymbol{w}$是法向量,$\boldsymbol{x}$是数据点,$b$是截距。
分别表示了超平面的方向、数据点和距离。
SVM训练的过程可以用拉格朗日乘数法进行求解,即将超平面分割成若干的小块,然后求出每个小块到超平面的距离。
这个最优的超平面是将不同类别之间的间隔最大化的超平面。
对于某些不能直接用超平面进行分割的数据,可以将其映射到高维空间中,从而将其转化为可分割的数据。
这种方法被称为核方法,常用的核函数有线性核、多项式核、高斯核等。
2. SVM的应用2.1 SVM的分类问题SVM广泛应用于分类问题中。
在学习的过程中,SVM要求确定最优分类面,包括分类面的形状和位置。
这个训练的过程被称为支持向量机(SVMs)。
对于一个简单的二分类问题,可以使用以下的公式:$$h(x) = \begin{cases}+1 & \text{if } \boldsymbol{w} \cdot \boldsymbol{x} + b \geq 0 \\-1 & \text{if } \boldsymbol{w} \cdot \boldsymbol{x} + b < 0 \\\end{cases}$$其中,$\boldsymbol{w}$和$b$是SVM的模型参数。
w支持向量机: Maximum Margin Classifierby pluskid, on 2010-09-08, in Machine Learning84 comments支持向量机即Support Vector Machine,简称SVM 。
我最开始听说这头机器的名号的时候,一种神秘感就油然而生,似乎把Support 这么一个具体的动作和Vector 这么一个抽象的概念拼到一起,然后再做成一个Machine ,一听就很玄了!不过后来我才知道,原来SVM 它并不是一头机器,而是一种算法,或者,确切地说,是一类算法,当然,这样抠字眼的话就没完没了了,比如,我说SVM 实际上是一个分类器(Classifier) ,但是其实也是有用SVM 来做回归(Regression) 的。
所以,这种字眼就先不管了,还是从分类器说起吧。
SVM 一直被认为是效果最好的现成可用的分类算法之一(其实有很多人都相信,“之一”是可以去掉的)。
这里“现成可用”其实是很重要的,因为一直以来学术界和工业界甚至只是学术界里做理论的和做应用的之间,都有一种“鸿沟”,有些很fancy 或者很复杂的算法,在抽象出来的模型里很完美,然而在实际问题上却显得很脆弱,效果很差甚至完全fail 。
而SVM 则正好是一个特例——在两边都混得开。
好了,由于SVM 的故事本身就很长,所以废话就先只说这么多了,直接入题吧。
当然,说是入贴,但是也不能一上来就是SVM ,而是必须要从线性分类器开始讲。
这里我们考虑的是一个两类的分类问题,数据点用x来表示,这是一个n维向量,而类别用y来表示,可以取1 或者-1 ,分别代表两个不同的类(有些地方会选0 和 1 ,当然其实分类问题选什么都无所谓,只要是两个不同的数字即可,不过这里选择+1 和-1 是为了方便SVM 的推导,后面就会明了了)。
一个线性分类器就是要在n维的数据空间中找到一个超平面,其方程可以表示为一个超平面,在二维空间中的例子就是一条直线。
svm算法公式摘要:一、SVM 算法简介1.SVM 算法定义2.SVM 算法的发展历程二、SVM 算法的基本思想1.最大间隔分类2.支持向量三、SVM 算法的核心公式1.线性可分情况下的SVM 公式2.线性不可分情况下的SVM 公式四、SVM 算法的实现与优化1.SVM 算法的实现流程2.SVM 算法的参数选择与优化五、SVM 算法的应用领域1.分类问题2.回归问题3.其他应用场景正文:一、SVM 算法简介支持向量机(Support Vector Machine,简称SVM)是一种经典的机器学习算法,主要用于分类和回归问题。
它通过寻找一个最优超平面,使得不同类别之间的样本点到该超平面的距离最大,从而实现分类。
SVM 算法具有良好的泛化能力,受到广泛关注。
二、SVM 算法的基本思想1.最大间隔分类SVM 算法基于最大间隔分类的思想,寻找一个最优超平面,使得不同类别之间的样本点到该超平面的距离最大。
这样,在训练样本上分类正确的样本距离超平面越远,分类错误的样本距离超平面越近,从而实现了对样本的分类。
2.支持向量支持向量是指距离超平面最近的那些样本点。
这些样本点对于确定超平面的位置至关重要。
在SVM 算法中,我们关心的是使得分类间隔最大的超平面,即支持向量。
三、SVM 算法的核心公式1.线性可分情况下的SVM 公式对于线性可分的情况,SVM 算法通过以下公式求解最优超平面:w = (α * y * x^T * x + β * I) ^ (-1) * α * yb = Σα * y其中,w 表示超平面的法向量,b 表示截距,α表示拉格朗日乘子,y 表示样本的类别,x 表示样本的特征。
2.线性不可分情况下的SVM 公式对于线性不可分的情况,SVM 算法采用核技巧,将线性问题转化为非线性问题。
具体公式如下:w = (α * y * Σ x_i * x_i^T + β * I) ^ (-1) * α * yb = Σα * y其中,x_i 表示样本的特征,Σ表示求和,y 表示样本的类别,α表示拉格朗日乘子,β表示正则化参数。
SVM RFE原理详解SVM RFE(Support Vector Machine Recursive Feature Elimination)是一种基于支持向量机(Support Vector Machine)的特征选择算法。
特征选择是机器学习中的重要步骤,其目的是从原始特征集合中选择出最具有代表性的特征,以提高模型的性能和泛化能力。
1. 支持向量机(SVM)支持向量机是一种监督学习算法,其主要任务是将训练数据集中的样本划分到不同的类别中。
SVM通过在特征空间中找到一个最优的超平面来实现分类任务。
超平面的选择是基于最大间隔的原则,即使得不同类别样本之间的距离最大化。
在SVM中,样本被表示为特征向量的形式,并且每个特征向量都有一个对应的类别标签。
SVM通过学习一个决策函数来进行分类,决策函数可以将新的样本点映射到特征空间,并根据其位置来预测其所属的类别。
2. 特征选择特征选择是为了降低维度,减少特征空间的复杂性,提高模型的性能和泛化能力。
在实际应用中,特征选择可以帮助我们发现最相关的特征,去除冗余和噪声特征,提高模型的解释性和可解释性。
特征选择的方法可以分为三类:过滤式(Filter)、包裹式(Wrapper)和嵌入式(Embedded)。
SVM RFE属于包裹式方法,其主要思想是将特征选择嵌入到模型训练过程中,通过迭代的方式逐步剔除不重要的特征。
3. SVM RFE算法步骤SVM RFE算法的基本步骤如下:步骤1:初始化首先,将原始特征集合作为输入,初始化SVM模型。
设定特征选择的目标维度。
步骤2:特征权重计算使用初始化的SVM模型对原始特征集合进行训练,并计算每个特征的权重。
这些权重反映了特征对模型性能的贡献程度,权重越大表示该特征越重要。
步骤3:特征剔除根据特征权重,剔除权重最小的特征。
通过剔除一个特征,得到新的特征集合。
步骤4:模型更新使用新的特征集合重新训练SVM模型,并计算特征权重。
机器学习:SVM公式推导
引⾔
对于SVM的⼤致原理之前已经讲过了,但是对于公式的推导,很多书都并未做要求,⽽且在实际应⽤过程中并未涉及过深,但鉴于台⼤机器学习课程中讲到了,⾃⼰为了巩固⾃⼰的学习,也梳理⼀遍SVM中公式的推导
此处考虑了C,也就是惩罚因⼦,不再是之前的hard-margin
推导过程
如果是soft-margin,那就说明我们能容忍⼀些错误,那么⽬标问题转化为
其中C⽐较⼤的时候,对离群点重视,越不要犯错越好,C⽐较⼩的时候,不是很看重离群点,重点在于找出margin越⼤越好
对于上⾯的问题我们⽆法求解,那么我们不妨转变⼀下思维,不去看犯了多少错误,⽽去看⼀共犯的错误有多⼤,⽤ξ记录违规了多少
此时的问题已经转换为⼆次规划问题了,对于⼆次规划问题⼜可以⽤之前的⽅法转换为对偶的⼆次规划问题了
同样是利⽤拉格朗⽇算法,由于有两组条件,所以需要两个参数α和β来作为拉格朗⽇乘⼦
为了求L的极值,我们得对这些变量求偏微分,⾸先我们对ξ做偏微分
得到β和C和α的关系,这样我们可以把β换掉,这样只考虑α
将β带进去得到:
这个式⼦如果不看条件的话跟hard margin的⼀样,这样的话我们可以对b,w做偏微分
这样我们得到α和yn的关系,以及w和α和yn以及zn的关系,带⼊式⼦中
问题就转换为跟原来差不多,只是α的条件多了⼀个C
然后把⼆次规划问题丢到QP解中可以解得到α,但是b的算法跟原来不⼀样,KKT条件已经变了主要是b怎么算,hard margin SVM中与soft的对⽐
主要是y和ξ那⼀项⽐较⿇烦
可以发现⽤free SV就可以消掉,于是b的计算⽅式还是⽤⽀持向量来算,也就是free SV
α的三种情形。