个人定位系统的地图匹配方法

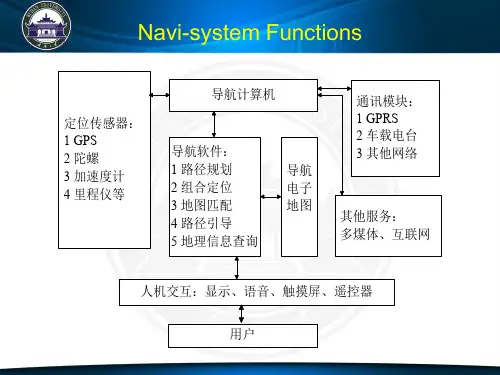
基于分布式坐标系统的地图匹配算法研究地图匹配算法是一种广泛应用于导航、交通管理、物流运输等领域的技术。

它通过将移动对象在现实世界中的位置映射到地图上，从而实现位置识别、路径规划等功能。

然而，由于移动对象在现实世界中的位置常常无法直接与地图上的节点一一对应，地图匹配算法面临着许多挑战。

本文将介绍一种基于分布式坐标系统的地图匹配算法，并解决其中涉及的一些难点问题。

一、分布式坐标系统分布式坐标系统是一种将地球表面划分为若干个二元组（纬度、经度）的坐标系统。

在传统的平面坐标系中，因为地球是一个椭球形的球体，同一纬度下每一经度的距离是不相等的，这对于地图匹配算法带来了许多困难。

而分布式坐标系统将地球看作一个无限细分的球体，每个点都可以被唯一地表示为一个二元组。

这种坐标系统可以轻松地解决跨越经线的问题，因此广泛应用于地图匹配算法中。

二、地图匹配算法地图匹配算法的本质是将现实世界中的位置信息与地图上的节点进行匹配。

在实际运用中，一些因素会对位置信息造成干扰，导致识别误差。

例如，位于城市建筑群密集区的移动对象可能会受到大楼阻挡而难以被识别。

一个好的地图匹配算法应该能够处理这些干扰因素，同时具有较高的匹配准确率和响应速度。

1、HMM算法HMM算法是最经典的地图匹配算法之一。

它将地图上的各条路段看作一个隐含状态，将移动对象在路段上的位置看作可观测状态。

通过计算不同观测状态出现的概率来确定移动对象所处的路段。

虽然HMM算法具有一些优势，例如对于平移、旋转、尺度变换等情况具有较高的稳定性，但它也存在着一些弊端。

例如，在复杂的交通网络中计算复杂度较高，同时需要进行大量的参数调优。

2、基于距离的匹配算法基于距离的匹配算法是另一种经典的地图匹配算法。

它将移动对象在现实世界中的位置与地图上的节点进行距离计算，找到与之距离最近的节点作为匹配结果。

虽然基于距离的匹配算法计算简单，但是它对定位误差比较敏感，同时无法准确处理移动对象沿路线行进的情况，导致误匹配率高。

智能导航与地图匹配算法研究第一章引言智能导航系统是现代社会中不可或缺的一部分，它通过利用先进的地图匹配算法，帮助用户快速准确地找到目的地。

本文旨在研究智能导航系统中的地图匹配算法。

第二章智能导航系统概述2.1 智能导航系统的定义与特点智能导航系统是一种利用计算机技术和地理信息系统技术，为用户提供路线规划、道路交通状况、兴趣点搜索等功能的导航系统。

其特点包括准确性、实时性、智能化和多功能性。

2.2 智能导航系统的应用领域智能导航系统广泛应用于汽车导航、行人导航、航空导航等领域。

它不仅在城市交通中起到路线规划的作用，还可以通过实时交通信息，提供最佳的导航方案。

第三章地图匹配算法概述3.1 地图匹配算法的定义与目的地图匹配算法是指将用户实际的轨迹数据与地图数据进行匹配的过程。

其目的是找到最佳的地图匹配路径，使导航系统能够准确地提供导航指引。

3.2 地图匹配算法的分类地图匹配算法可分为几何模型匹配算法和统计模型匹配算法两大类。

几何模型匹配算法包括距离匹配、角度匹配等，而统计模型匹配算法则利用概率统计方法进行匹配。

第四章地图匹配算法研究方法4.1 轨迹数据的获取与预处理地图匹配算法的研究离不开高精度的轨迹数据。

本文介绍了轨迹数据的获取方式，并对数据进行预处理，包括去除异常点、平滑处理等。

4.2 几何模型匹配算法研究方法几何模型匹配算法是地图匹配算法中最常用的方法之一。

本节介绍了距离匹配算法和角度匹配算法的研究方法，并比较了它们的优缺点。

4.3 统计模型匹配算法研究方法统计模型匹配算法在地图匹配中也有重要应用。

本节介绍了统计模型匹配算法的研究方法，包括隐马尔可夫模型、贝叶斯网络等，并分析了它们在实际中的应用。

第五章地图匹配算法的评估与改进5.1 地图匹配算法的评估指标地图匹配算法的评估指标包括匹配精度、匹配速度、鲁棒性等。

本节介绍了常用的评估指标，并对不同算法进行了性能评估。

5.2 地图匹配算法的改进方法地图匹配算法在实际应用中仍存在一些问题，如误差累积、定位误差等。

测绘技术中常见的地图配准算法介绍地图配准是测绘技术中的一个重要环节，它的主要目的是将多幅地图或者地理数据进行对应，使得它们在同一基准下具备一致性。

在实际的测绘应用中，地图配准算法能够帮助我们更加准确地理解和分析地理现象，为精确测绘和地理信息系统等应用提供支持。

本文将介绍一些常见的地图配准算法，以及它们的原理和应用。

一. 特征点匹配算法特征点匹配算法是地图配准中常用的一种方法。

该算法通过提取地图上的关键特征点，比如角点或者边缘点，然后在不同地图上寻找相应的特征点进行匹配。

在特征点匹配中，常用的算法包括克鲁斯卡尔算法、归一化互相关算法和改进的归一化互相关算法等。

克鲁斯卡尔算法是一种最小生成树的算法，它的主要思想是通过连接权值最小的边逐步构建最小生成树。

在地图配准中，我们可以将特征点作为节点，它们之间的相似度作为边的权值，然后使用克鲁斯卡尔算法寻找最佳的匹配组合。

归一化互相关算法是一种基于互相关的特征点匹配方法。

它通过计算两个特征点周围区域内的互相关系数来判断它们的相似度。

在进行配准时，我们可以选取特定阈值来筛选出相似度较高的特征点对，从而得到最佳的匹配结果。

改进的归一化互相关算法是针对传统归一化互相关算法的一种改进。

它在计算互相关系数时引入了自适应窗口大小和自适应核函数，从而提高了特征点匹配的准确性和鲁棒性。

改进的归一化互相关算法在地图配准和图像配准中都有广泛的应用。

二. 尺度不变特征变换算法尺度不变特征变换（Scale-Invariant Feature Transform，简称SIFT）算法是一种经典的特征点匹配算法，它在地图配准中也有较为广泛的应用。

SIFT算法通过分析图像的局部特征，如边缘和角点等，并在不同图像中寻找相应的特征点进行匹配。

SIFT算法的主要步骤包括尺度空间极值检测、关键点定位、方向分配、描述子生成和特征点匹配等。

在进行地图配准时，我们可以提取地图上的SIFT特征点，并在不同地图中进行匹配，从而得到两幅地图之间的对应关系。

地图匹配算法的流程和基本原理英文回答：## Map Matching Algorithm: Workflow and Basic Principles.Workflow:1. GPS Data Preprocessing: Cleaning and filtering raw GPS data to remove noise and outliers.2. Candidate Path Generation: Identifying potential paths the vehicle could have traversed using a road network database.3. Cost Calculation: Assigning weights to different features of the candidate paths (e.g., distance, speed, road type).4. Path Selection: Choosing the most likely path basedon the calculated costs.5. Smoothing: Adjusting the selected path to improveits smoothness and fit with the GPS data.Basic Principles:Dynamic Time Warping: Allowing non-uniform stretching and compression of GPS data points to align them with the road network.Cost Function Optimization: Minimizing a cost function that measures the discrepancy between the GPS data and the matched path.Heuristic Search: Employing techniques such as A or particle filtering to explore the candidate paths efficiently.Probabilistic Modeling: Incorporating probabilistic models to account for uncertainty in GPS data and path selection.Spatial Constraints: Utilizing spatial information (e.g., road segments, intersections) to guide the matching process.## Implementation Considerations.Choice of Cost Function: Different cost functions can be used depending on the application (e.g., distance,travel time, speed consistency).Candidate Path Selection: The size and accuracy of the road network database play a crucial role in generating reliable candidate paths.Smoothing Techniques: Smoothing algorithms (e.g., Kalman filtering, cubic splines) can improve the robustness and accuracy of the matched path.Computational Complexity: Map matching algorithms can be computationally intensive, especially for large datasets.中文回答：## 地图匹配算法，流程和基本原理。

测绘技术中的地图匹配与路径规划方法随着城市的扩张和交通网络的不断发展，人们对高精度地图和路径规划的需求日益增加。

在现代测绘技术中，地图匹配和路径规划是两个重要的研究领域。

地图匹配是指将实时采集的位置数据与地图数据进行对比，从而确定所处位置。

而路径规划则是基于地图数据，找到最优的行驶路径。

本文将探讨测绘技术中的地图匹配和路径规划方法，并讨论其应用和挑战。

一、地图匹配方法1.1 基于特征点的地图匹配基于特征点的地图匹配方法是一种常用的地图匹配技术。

该方法首先从地图数据中提取关键特征点，如交叉口、地标建筑物等，然后通过与实时采集的位置数据进行对比，找到最匹配的特征点，确定位置。

这种方法在城市密集区域的定位效果较好，但在稀疏区域或高速公路等没有明显特征点的地方仍存在一定困难。

1.2 基于路段匹配的地图匹配基于路段匹配的地图匹配方法通过将实时位置数据与离线地图数据进行对比，确定当前所处的路段。

这种方法通常基于地图路网的拓扑结构，通过计算位置与路段之间的距离、方向差等指标，找到最佳匹配路段。

然而，该方法对于复杂的道路网络和交叉口的处理较为困难，容易出现匹配错误。

1.3 基于概率模型的地图匹配基于概率模型的地图匹配方法是一种较为精确的地图匹配技术。

该方法通过建立概率模型，将实时位置数据与地图数据进行概率匹配，计算匹配的置信度，从而确定位置。

常用的概率模型包括贝叶斯滤波方法和粒子滤波方法等。

这种方法在定位精度和鲁棒性方面具有一定的优势，但计算复杂度较高。

二、路径规划方法2.1 最短路径算法最短路径算法是一种经典的路径规划算法，常用于寻找两个节点之间的最短路径。

其中，Dijkstra算法是一种著名的单源最短路径算法，适用于无负权边的图。

而Bellman-Ford算法则可以应用在有负权边的情况下。

这些算法通过动态规划的思想，逐步更新节点的最短路径，找到最优解。

2.2 A*算法A*算法是一种启发式搜索算法，常用于地图路径规划。

如何进行地理坐标系统的转换与匹配地理坐标系统（Geographic Coordinate System，简称GCS）是地球表面上用于准确地描述位置的一种坐标系统。

它使用经度和纬度两个参数来定义一个地点的位置。

然而，在不同的地图、GIS系统和数据源之间进行地理坐标系统的转换和匹配可以是一项复杂的任务。

本文将探讨如何进行地理坐标系统的转换与匹配，以实现地球表面位置的准确定位。

一、认识地理坐标系统地理坐标系统是基于椭球体模型的描述地球表面位置的一种坐标系统。

它使用经度和纬度这两个角度信息来确定地点的位置。

经度表示地点相对于本初子午线的偏移，可以是东经或西经；纬度则表示地点相对于赤道的偏移，可以是北纬或南纬。

这种坐标系统广泛应用于全球导航系统、地图制图和地理信息系统（GIS）中。

二、地理坐标系统的转换在不同的地图、GIS系统和数据源之间，往往存在着不同的地理坐标系统，因此需要进行坐标系统的转换，以实现位置信息的准确匹配和集成。

常见的地理坐标系统包括WGS84、北京54、西安80等，它们之间的转换需要通过一定的算法和参数进行。

1. 坐标系统的识别在进行地理坐标系统的转换之前，首先需要识别不同坐标系统之间的差异。

这可以通过查阅地图或数据源的元数据来获取。

元数据中通常会有关于坐标系统的描述信息，包括椭球体模型、投影方式、基准面等参数。

2. 参数的获取一旦识别出不同坐标系统之间的差异，就需要获取相应的转换参数。

这些参数可能包括椭球体参数、基准面参数、投影参数等。

可以通过专业软件、测绘局或地理空间数据提供商获取这些参数。

另外，也可以通过公开的坐标转换算法来计算这些参数。

3. 坐标转换算法地理坐标系统的转换通常依赖于一些基本的转换算法，比如大地坐标转换、投影坐标转换等。

这些算法基于数学模型和大量观测数据，通过一系列的运算和变换，将一个坐标转换为另一个坐标。

常见的算法有七参数转换、坐标纠正等。

4. 工具和软件进行地理坐标系统转换的过程中，可以使用一些专业的工具和软件来帮助完成。