双圆弧齿轮建模(proe)

齿轮零件建模齿轮传动是最重要的机械传动之一。

齿轮零件具有传动效率高、传动比稳定、结构紧凑等优点。

因而齿轮零件应用广泛，同时齿轮零件的结构形式也多种多样。

根据齿廓的发生线不同，齿轮可以分为渐开线齿轮和圆弧齿轮。

根据齿轮的结构形式的不同，齿轮又可以分为直齿轮、斜齿轮和锥齿轮等。

本章将详细介绍用Pro/E创建标准直齿轮、斜齿轮、圆锥齿轮、圆弧齿轮以及蜗轮蜗杆的设计过程。

3.1 直齿轮的创建3.1.1渐开线的几何分析图3-1 渐开线的几何分析渐开线是由一条线段绕齿轮基圆旋转形成的曲线。

渐开线的几何分析如图3-1所示。

线段s绕圆弧旋转，其一端点A划过的一条轨迹即为渐开线。

图中点（x1,y1）的坐标为：x1=r*cos(ang),y1=r*sin(ang) 。

(其中r为圆半径，ang为图示角度)对于Pro/E关系式，系统存在一个变量t，t的变化范围是0～1。

从而可以通过（x1,y1）建立（x,y）的坐标，即为渐开线的方程。

ang=t*90s=(PI*r*t)/2x1=r*cos(ang)y1=r*sin(ang)x=x1+(s*sin(ang))y=y1-(s*cos(ang))z=0以上为定义在xy平面上的渐开线方程，可通过修改x，y，z的坐标关系来定义在其它面上的方程，在此不再重复。

3.1.2直齿轮的建模分析本小节将介绍参数化创建直齿圆柱齿轮的方法，参数化创建齿轮的过程相对复杂，其中要用到许多与齿轮有关的参数以及关系式。

直齿轮的建模分析（如图3-2所示）：（1）创建齿轮的基本圆这一步用草绘曲线的方法，创建齿轮的基本圆，包括齿顶圆、基圆、分度圆、齿根圆。

并且用事先设置好的参数来控制圆的大小。

（2）创建渐开线用从方程来生成渐开线的方法，创建渐开线，本章的第一小节分析了渐开线方程的相关知识。

（3）镜像渐开线首先创建一个用于镜像的平面，然后通过该平面，镜像第2步创建的渐开线，并且用关系式来控制镜像平面的角度。

（4）拉伸形成实体拉伸创建实体，包括齿轮的齿根圆实体和齿轮的一个齿形实体。

双圆弧正弦曲线齿轮
（原创版）
目录
1.双圆弧正弦曲线齿轮的定义和特点
2.双圆弧正弦曲线齿轮的设计和制造
3.双圆弧正弦曲线齿轮的应用领域
4.双圆弧正弦曲线齿轮的优势和未来发展
正文
双圆弧正弦曲线齿轮是一种新型的齿轮设计，其齿廓曲线为双圆弧正弦曲线，具有出色的传动性能和承载能力。

双圆弧正弦曲线齿轮的设计和制造过程相对复杂，需要通过精细的数学计算和先进的制造技术来完成。

设计时需要考虑齿轮的材料、模数、压力角、齿数等因素，以确保齿轮的精度和可靠性。

制造过程中，需要采用高精度的机床和刀具，以实现齿轮齿廓的精确加工。

双圆弧正弦曲线齿轮广泛应用于各种工业设备和机械传动系统中，如减速器、变速器、电机、机床等。

其出色的传动性能和承载能力，使得它能够在各种恶劣的环境下稳定工作，大大提高了设备的运行效率和寿命。

双圆弧正弦曲线齿轮的优势主要体现在以下几个方面：首先，其齿廓曲线的特殊设计，使得齿轮的接触面积更大，承载能力更强；其次，其齿廓曲线的连续性，使得齿轮的传动噪声更小，运行更平稳；最后，其制造工艺的先进性，使得齿轮的精度和可靠性更高。

未来，双圆弧正弦曲线齿轮的发展前景广阔。

随着科技的不断进步和工业生产的不断发展，对齿轮的性能和质量要求越来越高。

第1页共1页。

对于新手来说，很可能都希望动手画一个齿轮，这是我在网上搜集并整理，然后动手亲自画出来的齿轮，希望对于新手有所帮助。

一、预备知识画一个M=4 ，Z=10 ，厚度为44的外啮合齿轮正常齿制：ha'=1，c'=0.25分度圆直径：d=m*z齿顶圆直径：da=(z+2ha')*m齿根圆直径：df=(z-2ha'-2c')*m (外啮合) df=(z+2ha'+2c')*m（内啮合）经计算：d=40，da=48，df=30最终效果如下：二、具体操作步骤如下1、拉伸一个直径为da=48，厚为44的圆柱体操作步骤：拉伸--选取Font面为草绘平面，绘制圆柱体，得到下图2、用笛卡儿方式插入基准曲线操作步骤：点击"插入基准曲线"按钮，选取"从方程"-"完成"，选取"坐标系"，再选取"笛卡儿"，出现记事本，在里面输入一下内容：然后保存，退出，此时模型出现蓝色的曲线，如下图3、选择步骤2的曲线，然后选取Top面进行镜像，得到如下图4、选取第二条曲线，即步骤3得到的曲线，然后"编辑"，"复制"，"选择性粘贴"，选择"旋转"，输入旋转角度((360/2/z)+1.74)，如下图5、选择第三条曲线，即步骤4得到的曲线，然后"编辑"，"复制"，"选择性粘贴"，选择"旋转"，输入旋转角度(-360/z)，得到如下图点击确定得到如下图6、用草绘按钮画曲线操作步骤：先画一个直径为df的齿根圆，使用"边"命令选取两条曲线和齿顶圆分别过两个八字型的曲线末端作切线，与齿根圆df分别交两点修剪多余的边，并给根部倒角R=0.2*m，得到如下图7、拉伸-去处材料，得到如下图8、阵列齿数，得到如下图。

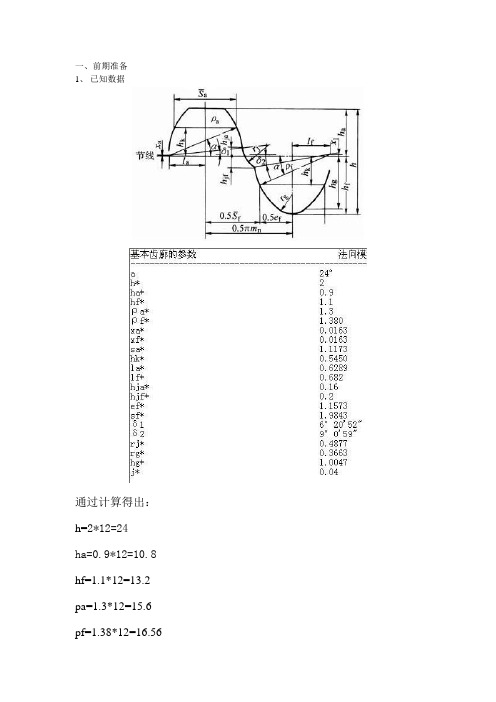
一、前期准备1、已知数据通过计算得出：h=2*12=24ha=0.9*12=10.8 hf=1.1*12=13.2 pa=1.3*12=15.6 pf=1.38*12=16.56xa=0.0163*12=0.1956xf=0.0163*12=0.1956sa=1.1173*12=13.4076hk=0.545*12=6.54la=0.6289*12=7.5468lf=0.682*12=8.184hja=0.16*12=1.92hjf=0.2*12=2.4ef=1.1573*12=13.8876sf=1.9843*12=23.8116rj=0.4877*12=5.8524rg=0.3663*12=4.3956hg=1.0047*12=12.0564计算校核数据：m n=12mm，m t=m n/cosβ=12/cos15935'''=12.43mm，z1=26，z2=122，β=15935'''d1=m n z1/cosβ=12×26/0.9652mm=323.249mmd2= m n z2/cosβ=12×122/0.9652mm=1516.784mmd a1=d1+2*h m n=323.249+2×0.9×12mm=344.849mmad a2=d2+2*h m n=1516.784+2×0.9×12mm=1538.384mmad f1=d1-2*h m=323.249-2×1.1×12mm=296.849mmf nd f2=d 2-2*f n h m =1516.784-2×1.1×12mm=1490.384mm a=()1212d d +=（323.249+1516.784）/2mm=920.0165mm b 1=455mm ，b 2=450mm2、CAXA 电子图版绘制齿廓基本图形齿廓基本图形啮合齿廓图形二、齿廓导入ＵＧ１、将文件另存为syhcl.dxf 并保存在非中文目录下 ２、启动UG8.0，新建文件，导入syhcl.dxf三、齿轮绘制过程1、利用移动对象命令，将图形旋转绕X轴旋转90度2、小轮齿宽455mm，大轮齿宽450mm，分别沿X轴拉伸两圆柱3、绘制螺旋线螺旋线导程：T=pi*D/tanB小齿轮：T=3.1415926*323.249/tan15.16=3748.0621大齿轮：T=3.1415926*1516.784/tan15.16=17587.06351、旋转坐标系螺旋线是沿Z向伸展的2、分别绘制两条螺旋线小齿轮大齿轮3、将大轮小轮齿廓图形投影至两圆柱后平面小轮投影结果大轮投影结果4、将齿廓图形分别向各自法向旋转15.16度，并将螺旋线再旋转出一条，以保证扫掠截面的一致性小轮大轮5、扫掠小齿轮齿廓截面，求差后进行特征分组小轮扫掠结果求差后结果特征分组选择扫掠和求差6、对特征分组执行阵列面命令阵列面结果7、扫掠大齿轮齿廓截面，求差后进行特征分组8、观察啮合状态。

Pro-e 齿轮教程第一步新建一个文件File > New... > 出现新建文件对话框> 输入新文件名：gear > OK第二步建立第一条曲线> Sketch | Done> 选择绘图平面：FRONT> OK> Top > 选择参考平面：TOP> 绘制如图剖面>> OK> 完成第一条曲线的绘制第三步修改曲线的名称Set Up > Name > Feature > 在模型树选择曲线> 输入新的名称：PITCH_DIAMETER> Done> 回到PART菜单第四步修改尺寸的名称Modify > 在模型树选择曲线> 在零件窗口出现尺寸，如图> DimCosmetics > Symbol > 选择尺寸，如图> 输入新的名称：PCD> Done> Done> 回到PART菜单第五步建立两个参数Set up > Parameters > Part > Create > Real Number> 输入第一个参数名称：m> 直接回车(由于这个参数的值是由方程控制的，所以这里不用输入数值) > Real Number> 输入第二个参数名称：no_of_teeth> 输入数值：25> Done/Return> Done> 回到PART菜单第六步输入方程式Relations > Add> 输入方程式：m=PCD/no_of_teeth > 回车> 再一次回车以结束方程式的输入> Done> 回到PART菜单第七步绘制第二条曲线> Sketch | Done> Use Prev> Okay> 绘制如图剖面>> OK> 完成第二条曲线的绘制第八步修改第二条曲线的名称Set Up > Name > Feature > 在模型树选择第二条曲线> 输入新的名称：ADDENDUM_DIAMETER> Done> 回到PART菜单第九步修改第二条曲线尺寸的名称Modify > 在模型树选择第二条曲线> 在零件窗口出现曲线的尺寸> DimCosmetics > Symbol > 选择第二条曲线的尺寸> 输入新尺寸名称：ADD_DIAMETER> Done> Done> 回到PART菜单第十步输入第二条方程式Relations > 选择第二条曲线> 这时零件窗口显示零件尺寸的名称，如图> Add> 输入方程式：ADD_DIAMETER=PCD+2*m > 回车> 再一次回车以结束方程式的输入> Done> 回到PART菜单第十一步绘制第三条曲线> Sketch | Done> Use Prev> Okay> 绘制如图剖面>> OK> 完成第三条曲线的绘制第十二步修改第三条曲线的名称Set Up > Name > Feature > 在模型树选择第三条曲线> 输入新的名称：DEDDENDUM_DIAMETER> Done> 回到PART菜单第十三步修改第三条曲线尺寸的名称Modify > 在模型树选择第三条曲线> 在零件窗口出现曲线的尺寸，如图> DimCosmetics > Symbol > 如图所示尺寸> 输入新尺寸名称：DED_DIAMETER> Done> Done> 回到PART菜单第十四步输入第三条方程式Relations > 选择第三条曲线> 这时零件窗口显示零件尺寸的名称，如图> Add> 输入方程式：DED_DIAMETER=PCD-2*(m+(3.1415*m/20)) > 回车> 再一次回车以结束方程式的输入> Done> 回到PART菜单第十五步绘制第四条曲线> Sketch | Done> Use Prev> Okay> 绘制如图剖面>> OK> 完成第四条曲线的绘制第十六步修改第四条曲线的名称Set Up > Name > Feature > 在模型树选择第四条曲线> 输入新的名称：BASE_DIAMETER> Done> 回到PART菜单第十七步修改第四条曲线尺寸的名称Modify > 在模型树选择第四条曲线> 在零件窗口出现曲线的尺寸，如图> DimCosmetics > Symbol > 如图所示尺寸>输入新尺寸名称：BASE_DIAMETER> Done> Done> 回到PART菜单第十八步建立一个参数Set up > Parameters > Part > Create > Real Number> 输入参数名称：pressure_angle> 输入数值：20> Done/Return> Done> 回到PART菜单第十九步输入第四条方程式Relations > 选择第四条曲线> 这时零件窗口显示零件尺寸的名称，如图> Add> 输入方程式：BASE_DIAMETER=PCD*cos(pressure_angle) > 回车> 再一次回车以结束方程式的输入> Done> 回到PART菜单第二十步建立第五条曲线> Sketch | Done> Use Prev> Okay> 绘制如图剖面>> OK> 完成第五条曲线的绘制第二十一步修改第五条曲线的名称Set Up > Name > Feature > 在模型树选择第五条曲线> 输入新的名称：TOOTH> Done> 回到PART菜单第二十二步修改第五条曲线尺寸的名称Modify > 在模型树选择第五条曲线> 在零件窗口出现曲线的尺寸> DimCosmetics > Symbol > 分别将对应的尺寸改成如图所示的名称> Done> Done> 回到PART菜单第二十三步建立方程式Relations > 选择第五条曲线> 这时零件窗口显示零件尺寸的名称，如图> Add> 输入方程式：TOOTH_RAD=PCD/8 > 回车> HALF_TOOTH_TK=3.1415*m/4 > 回车> TIP_RAD=3.1415*m/8 > 回车> 再一次回车以结束方程式的输入> Done> 回到PART菜单第二十四步建立两个参数Set up > Parameters > Part > Create > Real Number> 输入参数名称：helix_angle> 输入数值：15> Real Number> 输入参数名称：face_width> 输入数值：100> Done/Return> Done> 回到PART菜单第二十五步复制曲线Feature > Copy > Move | Select | Independent | Done> 选择TOOTH曲线> Done> Translate> Plane> 选择FRONT平面> Flip | Okay> 输入数值：face_width*cos(helix_angle)/3(注：这里可以用方程式代替，这里为了简便，就不写出来了，但我已给出完整的公式，你只需将公式代出相应的尺寸名称就可以了。

proe齿轮参数化画法直齿轮的建模过程1．输入基本参数和关系式（1）单击，在新建对话框中输入文件名“gear”,然后单击；（2)在主菜单上单击“工具”→ “参数”，系统弹出“参数”对话框，如图3-3所示；（3）在“参数”对话框内单击按钮，可以看到“参数”对话框增加了一行，依次输入新参数的名称、值、和说明等。

需要输入的参数如表3-1所示；注意：表3-1中未填的参数值，表示是由系统通过关系式将自动生成的尺寸，用户无需指定。

完成后的参数对话框如图3-4所示：（4）在主菜单上依次单击“工具”→“关系”，系统弹出“关系”对话框，如图3-5；（5）在“关系”对话框内输入齿轮的分度圆直径关系、基圆直径关系、齿根圆直径关系和齿顶圆直径关系。

由这些关系式，系统便会自动生成表3-1所示的未指定参数的值。

输入的关系式如下： ha=(hax+x)*mhf=(hax+cx-x)*md=m*zda=d+2*hadb=d*cos(alpha)df=d-2*hf完成后的“关系”对话框如图3-5所示；2．创建齿轮基本圆（1）在工具栏内单击按钮，系统弹出“草绘”对话框；（2）选择“FRONT”面作为草绘平面，选取“RIGHT”面作为参考平面，参考方向为向“左”，如图3-6所示。

单击【草绘】进入草绘环境；（3）在绘图区以系统提供的原点为圆心，绘制一个任意大小的圆，并且标注圆的直径尺寸。

在工具栏内单击按钮，完成草图的绘制；（4）在模型中右键单击刚刚创建的草图，在弹出的快捷菜单中单击选取“编辑”；（5）在主菜单上依次单击“工具”→ “关系”，系统弹出关系对话框，如图3-7所示；（6）在“关系”对话框中输入尺寸关系如下：D11=d其中D11为圆的直径尺寸代号，注意尺寸代号视具体情况会有所有同。

d为用户自定义的参数，即为分度圆直径。

通过该关系式创建的圆即为分度圆；（7）继续在工具栏内单击按钮，系统弹出“草绘”对话框；（8）在“草绘”对话框内单击按钮，进入草绘环境；（9）在绘图区以系统提供的原点为圆心，绘制一个任意大小的圆，并且标注圆的直径尺寸。

2024年第48卷第2期Journal of Mechanical Transmission双圆弧齿廓椭圆齿轮建模与运动学仿真袁新梅杨立昭黄天成唐伟（长江大学机械结构强度与振动研究所，湖北荆州434023）摘要为了满足齿轮变传动比运动、提高轮齿承载能力，结合齿轮啮合理论和双圆弧齿廓曲线结构参数特征，提出了一种新型双圆弧齿廓椭圆齿轮。

阐述了其节曲线的设计方法，利用Solid⁃Works软件建立了双圆弧齿廓椭圆齿轮三维模型；使用Adams软件对双圆弧齿廓椭圆齿轮副模型进行了运动学仿真，分析了不同偏心率对双圆弧椭圆齿轮副传动比变化规律的影响，并对比理论传动比曲线，分析了仿真传动比曲线存在波动误差的影响因素；为了减小齿轮副振动脉冲，给出了偏心率适当的取值范围。

本文的设计方法和分析结果对双圆弧齿廓非圆齿轮的参数化设计有理论参考价值，可为双圆弧齿廓椭圆齿轮副数控加工制造及应用提供依据。

关键词双圆弧齿廓椭圆齿轮运动学仿真变传动比Modeling and Kinematics Simulation of Elliptical Gears with Double CircularArc ProfilesYuan Xinmei Yang Lizhao Huang Tiancheng Tang Wei(Institute of Strength and Vibration of Mechanical Structures, Yangtze University, Jingzhou 434023, China)Abstract In order to meet the requirements of variable transmission ratios and improve the bearing capac⁃ity of gear teeth, a new type of double-circular-arc tooth profile elliptical gear is proposed based on the meshing theory and the structural parameter characteristics of the double-circular-arc tooth circular profile curve. The design method of its pitch curve is described. A three-dimensional model of the double-circular-arc tooth circu⁃lar profile elliptical gear is established using SolidWorks software. Adams software is used to simulate the kine⁃matics of the elliptical gear pair model with double-circular-arc tooth profiles, and the influence of different ec⁃centricities on the variation rule of the double-circular-arc gear pair transmission ratio is analyzed; compared with the theoretical transmission ratio curve, the influencing factors of the fluctuation error of the simulation transmission ratio curve are analyzed. In order to reduce the vibration pulse of the gear pair, the appropriate val⁃ue range of eccentricities is given. The design method and analysis results in this study have theoretical refer⁃ence value for parametric design of non-circular gears with double-circular-arc tooth profiles, and can provide a basis for NC manufacturing and application of elliptic gear pairs with double-circular-arc tooth profiles.Key words Double-circular-arc tooth profile Elliptic gear Kinematics simulation Variable trans⁃mission ratio0 引言非圆齿轮具有结构紧凑、效率高、工作可靠、寿命长的特点，可以传递动力和变传动比运动[1]，在机械系统中常用于实现换向、摆动、周期运转和间歇运动等功能。

PROE做齿轮运动仿真机构的详细过程齿轮运动仿真机构是一种用于实现齿轮系统运动仿真的装置，能够模拟齿轮和传动件在运动过程中的相对运动关系，用于预测和分析齿轮系统在不同工况下的运动性能和传动特性。

下面将详细介绍PROE（即现在多数被称为PTC Creo）软件制作齿轮运动仿真机构的过程。

第一步：建立齿轮模型1.打开PROE软件，选择“新建”新建一个零件。

2.根据实际齿轮的参数，使用绘图工具绘制齿轮的几何图形，包括齿数、齿轮直径、法向压力角等参数。

3.随后，利用特征操作命令，例如旋转、修剪、倒角等，对齿轮模型进行修整，使其符合实际需求。

第二步：建立约束1.在齿轮模型上选择一个轴线，作为齿轮运动的旋转轴。

2.新建一个“约束组”来管理后续创建的约束。

3.使用“旋转关节”命令将齿轮相对于旋转轴固定。

4.在约束组中继续创建其他约束，例如平行、垂直、距离等，以限制齿轮运动。

第三步：建立运动关系1.打开“运动关系”界面，选择“新建”创建一个新的运动关系。

2.根据需要，选择合适的运动类型，例如旋转、滑动等。

3.选择齿轮和其他关联几何体，建立相应的运动关系。

4.设定齿轮的运动参数，例如角速度、角加速度等。

第四步：修改齿轮模型参数1.在齿轮模型中修改各种参数，例如齿数、齿宽、模数等。

2.运用“更新”功能可以实时更新齿轮模型的几何形状及尺寸。

第五步：运行仿真1.进入“运动仿真”界面，点击“运行”按钮开始仿真。

2.根据所建立的运动关系和约束，仿真系统会模拟齿轮的运动过程。

3.可以观察到齿轮与齿轮之间的相对运动、接触点位置等。

4.在仿真过程中可以调整参数，观察不同参数对齿轮运动的影响。

第六步：分析仿真结果1.在仿真过程中会生成大量的仿真数据，可以用于分析齿轮系统的运动性能。

2.可以查看齿轮之间的接触应力、摩擦力、扭矩等数据。

3.根据仿真结果评估齿轮系统的传动效率、功耗、噪声等特性。

第七步：优化设计1.根据分析结果，对齿轮系统进行优化设计。

第3章齿轮零件齿轮传动是最重要的机械传动之一。

齿轮零件具有传动效率高、传动比稳定、结构紧凑等优点。

因而齿轮零件应用广泛，同时齿轮零件的结构形式也多种多样。

根据齿廓的发生线不同，齿轮可以分为渐开线齿轮和圆弧齿轮。

根据齿轮的结构形式的不同，齿轮又可以分为直齿轮、斜齿轮和锥齿轮等。

本章将详细介绍用Pro/E创建标准直齿轮、斜齿轮、圆锥齿轮、圆弧齿轮以及蜗轮蜗杆的设计过程。

3.1直齿轮的创建3.1.1渐开线的几何分析图3-1 渐开线的几何分析渐开线是由一条线段绕齿轮基圆旋转形成的曲线。

渐开线的几何分析如图3-1所示。

线段s绕圆弧旋转，其一端点A划过的一条轨迹即为渐开线。

图中点（x1,y1）的坐标为：x1=r*cos(ang),y1=r*sin(ang) 。

(其中r为圆半径，ang为图示角度)对于Pro/E关系式，系统存在一个变量t，t的变化范围是0～1。

从而可以通过（x1,y1）建立（x,y）的坐标，即为渐开线的方程。

ang=t*90s=(PI*r*t)/2x1=r*cos(ang)y1=r*sin(ang)x=x1+(s*sin(ang))y=y1-(s*cos(ang))z=0以上为定义在xy平面上的渐开线方程，可通过修改x，y，z的坐标关系来定义在其它面上的方程，在此不再重复。

3.1.2直齿轮的建模分析本小节将介绍参数化创建直齿圆柱齿轮的方法，参数化创建齿轮的过程相对复杂，其中要用到许多与齿轮有关的参数以及关系式。

直齿轮的建模分析（如图3-2所示）：（1）创建齿轮的基本圆这一步用草绘曲线的方法，创建齿轮的基本圆，包括齿顶圆、基圆、分度圆、齿根圆。

并且用事先设置好的参数来控制圆的大小。

（2）创建渐开线用从方程来生成渐开线的方法，创建渐开线，本章的第一小节分析了渐开线方程的相关知识。

（3）镜像渐开线首先创建一个用于镜像的平面，然后通过该平面，镜像第2步创建的渐开线，并且用关系式来控制镜像平面的角度。

（4）拉伸形成实体拉伸创建实体，包括齿轮的齿根圆实体和齿轮的一个齿形实体。

双圆弧正弦曲线齿轮摘要：1.双圆弧正弦曲线齿轮的概述2.双圆弧正弦曲线齿轮的特点与应用3.双圆弧正弦曲线齿轮的制造工艺4.双圆弧正弦曲线齿轮的优缺点分析5.双圆弧正弦曲线齿轮在我国的发展前景正文：一、双圆弧正弦曲线齿轮的概述双圆弧正弦曲线齿轮，是一种新型齿轮设计，其齿面为双圆弧形状，齿廓线为正弦曲线。

这种齿轮在传动过程中具有较高的平稳性和传动效率，逐渐在我国齿轮制造业中崭露头角。

二、双圆弧正弦曲线齿轮的特点与应用1.高平稳性：双圆弧正弦曲线齿轮的齿面形状和齿廓线设计使其在传动过程中具有较低的振动和噪音，提高了传动的平稳性。

2.高传动效率：双圆弧正弦曲线齿轮的齿廓线设计使其在啮合过程中齿面接触面积较大，减小了齿面滑动，从而提高了传动效率。

3.抗疲劳性能好：双圆弧正弦曲线齿轮的齿面形状和材料选择使其具有良好的抗疲劳性能，延长了齿轮的使用寿命。

4.应用广泛：双圆弧正弦曲线齿轮广泛应用于各类传动装置，如减速器、变速器等，尤其适用于高精度、高扭矩、低噪音的传动场合。

三、双圆弧正弦曲线齿轮的制造工艺1.锻造：通过锻造工艺生产出齿轮的毛坯，为后续加工提供基础。

2.粗加工：采用车削、铣削等加工方法，初步加工出齿轮的齿形。

3.精加工：采用齿轮磨削、滚齿等精密加工方法，精确加工出齿轮的齿形。

4.热处理：对齿轮进行热处理，提高齿轮的硬度和强度。

5.装配：将齿轮与传动轴等其他部件装配在一起，形成完整的传动系统。

四、双圆弧正弦曲线齿轮的优缺点分析优点：1.平稳性好，噪音低。

2.传动效率高，节省能源。

3.抗疲劳性能好，使用寿命长。

4.适应性强，应用范围广。

缺点：1.制造工艺复杂，成本较高。

2.对材料性能要求较高，材料成本增加。

五、双圆弧正弦曲线齿轮在我国的发展前景随着我国科技实力的不断提升和制造业的快速发展，双圆弧正弦曲线齿轮在我国的应用将越来越广泛。

此外，我国正大力推动绿色制造和智能制造，双圆弧正弦曲线齿轮的高传动效率和低噪音特性使其成为未来传动领域的重要研究方向。