有限元强度折减法

有限元强度折减系数法计算土坡稳定安全系数的精度研究摘要：有限元强度折减系数法在边坡稳定分析中的应用正逐渐受到人们的重视。

本文较为全面地分析了土体屈服准则的种类、有限元法自身计算精度以及H(坡高)、β(坡角)、C(粘聚力)、Φ(摩擦角)对折减系数法计算精度的影响，并给出了提高计算精度的具体措施。

通过对106个算例的比较分析，表明折减系数法所得稳定安全系数比简化Bishop法平均高出约5.7%，且离散度极小，这不仅验证了文中所提措施的有效性，也说明了将折减系数法用于分析土质边坡稳定问题是可行的。

关键词：强度折减系数边坡稳定屈服准则误差分析自弗伦纽期于1927年提出圆弧滑动法以来，至今已出现数十种土坡稳定分析方法，有极限平衡法、极限分析法、有限元法等。

不少研究表明，各种方法所得稳定安全系数都比较接近，可以说，这些方法已经达到了相当高的精度。

近年来，由于计算机技术的长足发展，基于有限元的折减系数法在边坡稳定分析中的应用备受重视。

与极限平衡法相比，它不需要任何假设，便能够自动地求得任意形状的临界滑移面以及对应的最小安全系数，同时它还可以真实的反映坡体失稳及塑性区的开展过程。

到目前为止，已有很多学者对折减系数法进行了较为深入的研究[1,2,3]，并在一些算例中得到了与极限平衡法十分接近的结果。

但总体说来，此法仍未在工程界得到确认和推广，究其原因在于影响该法计算精度的因素很多，除了有限元法引入的误差外，还依赖于所选用的屈服准则。

此论文');">论文的目的有两点：(1)力图全面分析屈服条件和有限元法本身对折减系数法计算精度的影响，并提出应选用何种屈服准则以及提高有限元法计算精度的具体措施；(2)结合工程实例，分析对边坡稳定安全系数影响最大的4个主要参数(H坡高、β坡角、C粘聚力、Φ摩擦角)对折减系数法计算精度的影响。

从以往的计算结果来看，严格法(Spencer)所得稳定安全系数比简化Bishop法平均高出约2%～3%，而通过106个算例的比较分析，表明：折减系数法所得稳定安全系数比简化Bishop法平均高出约5.7%，且误差离散度极小，可以认为是正确的解答[4]。

基于有限元强度折减法的边坡稳定性分析报告学院：土木工程与力学学院专业：结构工程姓名：学号：2016年7月有限元强度折减法研究进展摘要：在边坡稳定性分析中，相比于传统的极限平衡法、极限分析法等，有限元强度折减法具有明显的优势。

这主要体现在其无须事先假定滑动面的形状和位置，只需通过不断降低边坡岩土体的强度参数，进而使边坡岩土体因抗剪强度不能抵抗剪切应力而发生破坏，并最终得到边坡的最危险滑动面及相应的安全系数。

有限元强度折减法兼有数值计算方法和传统极限平衡方法的优点。

本文介绍了有限元强度折减法的原理与主要研究现状，并对其中的一些重点问题进行了研究与总结。

关键词：强度折减法;有限元;边坡稳定1 有限元强度折减法基本原理所谓强度折减，就是在理想弹塑性有限元计算中将边坡岩土体抗剪切强度参数逐渐降低直到其达到破坏状态为止，程序可以自动根据弹塑性计算结果得到破坏滑动面(塑性应变和位移突变的地带)，同时得到边坡的强度储备安全系数ω, 于是有:==。

'/,tan'tan/c cωϕϕω一般地，强度折减弹塑性有限元数值分析方法考察边坡稳定性的步骤是：首先对于某一给定的强度折减系数，通过逐级加载的弹塑性有限元数值计算确定边坡内的应力场、应变场或位移场，并且对应力、应变或位移的某些分布特征以及有限元计算过程中的某些数学特征进行分析，不断增大折减系数，直至根据对这些特征的分析结果表明边坡己经发生失稳破坏，将此时的折减系数定义为边坡的稳定安全系数。

尽管强度折减有限元法在边坡稳定性分析中得到重视与发展，但其计算中需要采用一定的边坡失稳评判标准来确定边坡失稳的临界状态，但是，各种判据的选用至今并没有取得统一。

2 主要研究现状强度折减概念由Zienkiewicz最早提出并用于边坡的稳定性分析，受限于当时数值计算和计算机水平而未能得到大的发展，直到近十几年来，随着数值计算和计算机技术的迅猛发展，强度折减法也得到了极大的发展，国内外许多学者在这方面做了大量的工作。

求解安全系数的有限元法
在边坡稳定性分析中，有限元法（Finite Element Method, FEM）被广泛用于求解土坡的安全系数。

安全系数是衡量边坡稳定性的指标，它代表了边坡实际的抗滑力与潜在滑动力之间的比值。

传统的极限平衡法通过确定可能的滑动面并计算作用于该面上的剪切强度和力矩平衡来估算安全系数。

然而，在有限元框架下，求解安全系数通常采用以下两种方法：
1. **有限元强度折减法 (Finite Element Strength Reduction Method, FSRM)**：
- 此方法基于逐步减少土体材料的抗剪强度参数（如内摩擦角或粘聚力），模拟土体逐渐趋向破坏的过程。

- 在每个折减步长上，重新进行有限元分析以获得新的位移场和应力状态。

- 当土体出现明显的塑性流动或达到预设的位移增量时，停止折减过程，并根据最后一次非线性迭代的结果计算出相应的安全系数。

- 这种方法得到的安全系数往往偏高，因为它考虑了整个土体的非线性响应，而非仅限于单一滑动面。

2. **结点位移法**：
- 结点位移法也是强度折减法的一种形式，通过监测随着抗剪强度降低，某些关键节点（如可能的滑裂带上的节点）的位移变化情况。

- 当位移突然增大时，表示潜在的滑动面已接近失稳状态，此时的抗剪强度折减比例可以用来反推安全系数。

有限元迭代解法也可以应用于边坡稳定分析中的复杂问题，例如当滑动面不明确或者滑动模式非常复杂时。

这种方法要求更为精细的网格划分和更为严谨的收敛条件控制，确保计算结果的准确性和可靠性。

总第３１８期交　通　科　技ＳｅｒｉａｌＮｏ．３１８　２０２３第３期ＴｒａｎｓｐｏｒｔａｔｉｏｎＳｃｉｅｎｃｅ＆ＴｅｃｈｎｏｌｏｇｙＮｏ．３Ｊｕｎｅ．２０２３ＤＯＩ１０．３９６３／ｊ．ｉｓｓｎ．１６７１ ７５７０．２０２３．０３．００５收稿日期：２０２３ ０２ １４第一作者：凌立鑫（１９８７－），男，硕士，高级工程师。

吉林省交通科技研发项目（山区高等级公路建设关键技术研究）资助基于有限元强度折减法的粗粒料路堤稳定性研究凌立鑫１　丰土根２（１．苏交科集团股份有限公司　南京　２１００００；　２．河海大学岩土工程研究所　南京　２１００００）摘　要　为研究山区高等级公路粗粒料高路堤填筑及质量控制关键技术，采用有限元强度折减法对综合位移失稳判据分析粗粒料路堤稳定的适用性及参数影响情况。

结果表明，综合位移失稳判据在粗粒料路堤稳定有限元强度折减分析中是可行的，基于综合位移失稳判据所得的安全系数随剪胀角的增大而增大，随荷载分级次数的增加而增大，随折减范围的减小而增大。

关键词　粗粒料　强度折减　失稳判据　剪胀角　荷载分级　折减范围　安全系数中图分类号　Ｕ４１６．１＋２ 目前，边坡稳定分析的主要方法是极限平衡法和有限单元法。

强度折减法作为有限单元法的一类，计算边坡稳定时的关键问题之一是用什么标准判别失稳，即选用何种失稳判据。

目前已提出的失稳判据主要有３种：有限元数值计算的收敛性，广义剪应变贯通、塑性区的范围及连通状态，边部特征部位的位移或最大位移。

国内外学者基于边坡特征部位的位移或最大位移已开展了一些研究。

Ｚｉｅｎｋｉｅｓｉｃｅ等［１］在最初使用有限元强度折减法时提出的失稳判据即最大节点位移。

宋二祥［２］将坡顶位移折减系数曲线水平段对应的折减系数作为安全系数。

关立军［３］通过算例分析发现当土的抗剪强度折减到一定程度后，土体位移会持续增大，折减系数与坡顶的水平位移关系曲线趋于平缓，并由此提出将边坡的“破坏程度”定义为强度折减系数与坡顶水平位移关系曲线斜率的函数，当斜率达到某一固定值时，认为边坡达到“破坏”状态。

边坡稳定分析中有限元强度折减法的发展与应用摘要：抗剪强度折减有限元法是抗剪强度折减法和有限元法的结合，常用于边坡稳定性分析中。

通过对边坡非线性有限元模型进行强度折减，使边坡达到不稳定状态，此时的折减系数就是稳定安全系数，同时可得到边坡破坏时的滑动面。

传统条分法无法获得岩质边坡的滑动面与稳定安全系数。

该方法开创了求岩质边坡滑动面与稳定安全系数的先例。

文章对此法的发展、基本原理以及影响因素进行了阐述，证实了其用于工程的可行性并分析总结出各因素对安全系数的不同影响，并结合自己的理解，对目前存在的部分问题提出一些建议。

关键词：边坡稳定分析；有限元强度折减法；屈服准则；安全系数引言边坡稳定分析是经典土力学最早试图解决而至今仍未圆满解决的课题，在中国水电工程建设中，边坡问题尤为突出，可能成为工程建设的制约性因素。

各种稳定分析方法在国内外水平大致相当，对于均质土坡，传统方法主要有：极限平衡法、极限分析法和滑移线场法等。

就目前工程应用而言，主要还是极限平衡法，但需要事先知道滑动面位置和形状。

对于岩质边坡，由于实际岩体中含有大量不同构造、产状和特性等不连续结构面(比如层面、节理、裂隙和软弱夹层等)，给岩质边坡的稳定分析带来了巨大的困难。

目前的各种数值分析方法，一般只是得出边坡应力、位移、塑性区，也无法得到边坡危险滑动面以及相应的安全系数[1]。

随着计算机技术的发展，尤其是岩土材料的非线性弹塑性有限元计算技术的发展，有限元强度折减法受到越来越多的关注。

1 发展背景自20世纪20年代以来，岩土工程的极限分析方法蓬勃发展，并广泛应用于工程实际。

有限元法数值方法适应性强，应用范围宽，但无法求出工程设计中十分有用的稳定安全系数F与极限承载力，从而制约了其在岩土工程中的应用。

1975年，英国科学家Zienkiewicz提出在有限元中采用增加荷载或降低岩土强度的方法来计算岩土工程的极限荷载和安全系数F[2]。

20世纪80年代、90年代曾用于边坡和地基的稳定分析[3]，但是由于当时缺少严格可靠、功能强大的大型有限元程序以及强度准则的选用和具体操作技术掌握不够等原因，导致计算精度不足，而没有得到岩土工程界的广泛采纳。

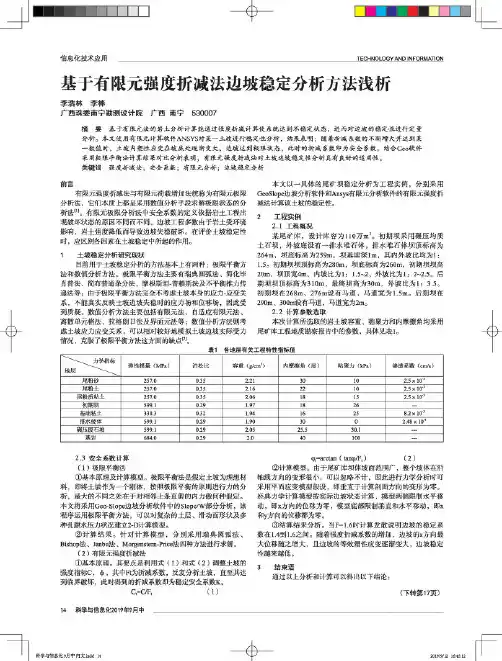
信息化技术应用TECHNOLOGY AND INFORMATION 基于有限元强度折减法边坡稳定分析方法浅析李浩林李棒广西珠委南宁勘测设计院广西南宁530007摘要基于有限元法的岩土分析计算能通过强度折减计算使系统达到不稳定状态，进而对边坡的稳定性进行定量分析。

本文使用有限元计算软件ANSYS对某一土坡进行稳定性分析，结果表明：随着折减系数的不断增大并达到某一数值时，土坡内塑性应变在坡底处逐渐变大，边坡达到极限状态，$匕时的折减系数即为安全系数。

结合Geo软件采用极限平衡法计算结果对比分析表明，有限元强度折减法对土坡边坡稳定性分析具有良好的适用性。

关键词强度折减法；安全系数；有限元分析；边坡稳定分析-1-C_1—刖旨有限元强度折减法与有限元荷载增加法统称为有限元极限分析法，它们本质上都是采用数值分析手段求解极限状态的分析法E。

有限元极限分析法中安全系数的定义依据岩土工程出现破坏状态的原因不同而不同。

边坡工程多数由于岩土受环境影响，岩土强度降低而导致边坡失稳破坏。

在评价土坡稳定性时，应区别各因素在土坡稳定中所起的作用。

1土坡稳定分析研究现状目前用于土坡稳定分析的方法基本上有两种：极限平衡方法和数值分析方法。

极限平衡方法主要有瑞典圆弧法、简化毕肖普法、简布普通条分法、摩根斯坦-普赖斯法及不平衡推力传递法等；由于极限平衡方法完全不考虑土坡本身的应力-应变关系，不能真实反映土坡边坡失稳时的应力场和位移场，因此受到质疑。

数值分析方法主要包括有限元法、自适应有限元法、离散单元格法、拉格朗日法及界面元法等；数值分析方法则考虑土坡应力应变关系，可以相对较好地模拟土坡边坡实际受力情况，克服了极限平衡方法这方面的缺点冋。

本文以一具体的尾矿坝稳定分析为工程实例，分别采用GeoSlope边坡分析软件和Ansys有限元分析软件的有限元强度折减法计算该土坡的稳定性。

2工程实例2.1工程概况某尾矿库，设计库容为110万n?。

基于 ANSYS的有限元强度折减法确定边坡安全系数摘要：本文基于ANSYS，采用D-P外角点外接圆屈服准则对国内某矿区边坡进行稳定性计算分析，通过不断对边坡强度参数黏聚力和内摩擦角进行折减，直到软件计算不收敛为止，其折减的倍数即为边坡稳定安全系数。

计算结果显示，利用ANSYS自带D-P本构模型计算得到的边坡安全系数远大于极限平衡法计算得到的边坡安全系数。

最后应用不同屈服准则安全系数的转换关系得到该边坡平面应变下与M-C匹配的D-P准则的安全系数，并与极限平衡法结果对比，吻合较好。

据此得出结论：在估算边坡安全系数方面，采用有限元强度折减法是一种值得信赖的方法，但计算中采用理想弹塑性材料模型时，屈服准则的选择会对边坡安全系数的计算产生较大影响。

关键词：有限元；强度折减；屈服准则；边坡稳定；安全系数1 引言目前，边坡稳定性分析发方法较多，主要有定性分析法（图解法、类比法）、定量分析法（极限平衡法、数值分析法）、非确定分析法（模糊分析评判法、可靠性分析法）。

而对于边坡安全系数，许多学者大多用定量分析法[1-2]。

传统的极限平衡法首先要确定一个潜在的滑动面，基于一系列简化假定后，由力系平衡或能量守恒求得滑动面的安全系数，用它作为评价边坡安全性的指标。

这些方法有瑞典条分法、简化毕肖普法、简布法、不平衡系数传递法等。

这些方法的基本出发点是一样的，即刚塑性假定，不同之处在于对条间力所作的假定不同。

由于这些假定的物理意义不一样，因此它们所能满足的平衡条件也不相同，计算步骤有繁有简，为了检验所列的各方法和其他边坡稳定性分析方法的精确性，许多学者在过去几十年里从不同角度做了大量研究并进行了系统总结[3-7]。

传统的极限平衡法由于没有考虑土体内部应力与应变的关系，故无法模拟分析土体发生变形甚至破坏的过程。

随着计算机技术的发展，数值计算方法在边坡稳定分析中得到了广泛的应用。

其最大的优点是求解安全系数时，不需要假定滑移面的形状和位置，也无需进行条分，可以分析任何形状的几何体，不但能进行线性分析还可进行非线性分析。

基于有限元强度折减法的土质边坡稳定性分析通过求解安全系数的原理，分析土质边坡的稳定性。

采用ANSYS有限元分析软件，根据莫尔-库仑六边形外接圆DP屈服准则，基于强度折减原理求解土质边坡的安全系数。

该方法通过不断折减安全系数，并不断判断边坡系统的稳定性，当计算不收敛时，可推断该系统正处于稳定至不稳定的临界状态，则该时刻对应的折减系数可判断为该边坡的安全系数。

基于此，可以判定土质边坡在不同外部荷载和自重作用下的稳定性。

该方法简单易懂，并具有较强的工程实践性。

标签：边坡安全系数；有限元分析方法；强度折减原理；屈服准则1 引言近年来随着工程的不断增加，边坡稳定性研究日益重要，日常通常使用的边坡稳定方法主要有塑性极限分析法、极限平衡法等。

而日前常用的研究方法都存在一定的弊端，比如以上几种研究方法都是基于极限平衡理论基础上分析土体，假定滑裂面为理想的圆弧状、折线状等，没有考虑到土体结构自身的应力-应变关系，无法队边坡的实际破坏和发展进行过程分析，同时也无法考虑到土体和支档共同作用及其变形协调。

而有限元强度折减法不仅可以针对各种形态复杂的边坡进行计算，模拟出土体与支护共同作用过程，同时可以模拟出土体失稳过程及滑移面总装，求出土体的应力-应变关系，同时可以结合土体的非线性本构关系，使计算结果与现实更为接近。

2 有限元强度折减安全系数定义通过ansys分析软件，不断降低土质边坡的С、φ值，直至破坏时，С、φ降低倍数w就是安全系数。

对于摩尔-库仑材料，强度折减安全系数可表示为：3 基本原理3.1 D-P准则目前新型的有限元软件为ANSYS，该软件采用的为德鲁克-普拉格准则，即D-P准则，该理论较其他理论更强调了体积应力、剪应力及中间主应力共同作用下对岩石力学强度的影响，也更能反映工程实际情况。

式中I1，J2分别为应力张量的第一不变量和应力偏张量的第二不变量。

这是一个通用表达式，通过变换α，k的表达式就可以在有限元中实现不同的屈服准则。

有限元强度折减法在岩土工程中的应用文章分析了有限元强度折减法在岩土工程中的应用优势，探析了有限元强度折减法在岩土工程中的应用，旨在为岩土工程相关工作人员提供一定的参考。

标签：有限元强度折减法岩土工程应用1前言英国科学家Zienkiewicz提出了用降低岩土强度或者增加外荷载，进行岩土工程安全系数的计算，该种方法被看做为岩土工程极限分析有限元法的雏形。

有限元强度折减法是极限分析有限元法最常用的方法之一，并且经过多年的实践应用获得了非常好的应用成果。

因此，文章针对有限元强度折减法在岩土工程中应用的研究具有非常重要的现实意义。

2有限元强度折减法在岩土工程中的应用优势分析（1）考虑周全。

有限元强度折减法在岩土工程中的应用，考虑问题比较周全，尤其是在细节方面，能够更加接近实际状况，在进行计算的过程中，计算数值越接近实际状况，其价值越高，能够有效的降低计算误差。

正是由于有限元折减法的这点优势，接近实际状况的计算方法，越来越被岩土工作者所青睐。

（2）适应性强。

我国幅员辽阔，涉及的地形包括高原、高山、山丘、平原等，一些岩土工程的测量工作会涉及到多种地形，如果采用传统的方法进行计算，不仅会增加工作人员的劳动强度，还会影响计算的精度，通过将有限元强度折减法应用在岩土工程测量中，通过分析相关地形，描述该地区地形的范围，以此评估相关地形的稳定性，无论施工现场的地形如何复杂，气候条件多恶劣，工作人员都可以在实验室中轻松的测量。

有限元强度折减法还有一个好处就是化整体为部分、化大为小，这样能够有效的降低工作人员的工作压力，降低计算过程中误差。

（3）准确性高。

国内岩土工程企业非常多，如果工程测量和计算的准确性较低，将会影响岩土工程企业的市场竞争力。

准确度是岩土工程测量中的必备条件，通过实践证明，有限元强度折减法在岩土工程测量中的应用，其结算结果比其他公式计算的结果更加准确，避免了其他公式就是你误差导致的误判，甚至导致地质变软以及工程坍塌等。

三维有限元强度折减法在岩质边坡稳定性分析的应用研究的开题报告一、选题背景岩质边坡的稳定性分析是岩土工程领域的重要研究方向之一。

随着计算机技术和数值模拟方法的不断进步，三维有限元法成为了岩质边坡稳定性分析的主流方法之一。

然而，三维有限元法在边坡分析中的应用受到了诸多因素的制约，例如计算量大、计算时间长等。

为了克服这些问题，学术界提出了强度折减法，即通过对模型中一些无关紧要的部分进行削减或简化，来减少计算量和计算时间。

强度折减法已经在岩石力学、煤岩岩体稳定性、深部岩体开挖等领域取得了较好的应用效果。

因此，本研究拟采用三维有限元强度折减法来分析岩质边坡的稳定性，探索强度折减法在岩质边坡分析中的应用效果。

二、研究内容及方法本研究的研究内容主要包括以下几个方面：1. 岩质边坡的稳定性分析方法探讨2. 三维有限元强度折减法的理论基础和原理分析3. 利用三维有限元软件建立岩质边坡模型并进行强度折减分析4. 分析不同折减方案对边坡稳定性的影响5. 分析岩质边坡的变形和破坏机制本研究采用文献调研和实验仿真相结合的研究方法。

首先，通过文献调研学习岩质边坡的稳定性分析方法和三维有限元强度折减法的理论基础。

然后，利用三维有限元软件建立岩质边坡模型，并对模型进行强度折减分析，观察不同折减方案对边坡稳定性的影响。

最后，分析岩质边坡的变形和破坏机制。

三、研究意义通过采用三维有限元强度折减法来分析岩质边坡的稳定性，可以有效减少计算量和计算时间，提高分析效率和精度。

同时，本研究可为岩质边坡稳定性分析提供新的思路和方法，对于岩土工程领域的理论研究和实际工程运用具有重要的意义。

四、预期成果本研究预期实现以下几个方面的成果：1. 探讨三维有限元强度折减法在岩质边坡稳定性分析中的应用原理和方法。

2. 建立合理的岩质边坡模型，并对模型进行强度折减分析。

3. 分析强度折减对边坡稳定性的影响，探索最优的折减方案。

4. 分析岩质边坡的变形和破坏机制，提供较为准确的预测和分析结果。

边坡稳定性分析中的有限元强度折减法安全系数
边坡稳定性分析中的有限元强度折减法安全系数
算方法、与传统极限平衡法相比所具有的优势、边坡失稳判据以及计算结果的影响因素。

采用有限元分析软件Plaxis进行强度折减计算，直至满足位移不收敛，从而得到边坡稳定安全系数。

论文关键词：边坡稳定,有限元强度折减法,失稳判据,安全系数
0.引言
边坡稳定性分析是岩土工程中一个十分重要的问题。

常用的边坡稳定性分析方法很多，如传统边坡稳定分析方法有:极限平衡法,极限分析法,滑移线场法等。

到目前极限平衡法已经日趋完善,基于该原理的新方法的不同仅是在条间力的假设上不同。

该法简单易用，为实际工程中广泛采用。

但是它没有考虑土体的应力应变特性,还要假设潜在滑面(如面、折线形、圆弧滑动面、对数螺线柱面等),对同一工程问题算不出一致的解。

极限分析法中的上限法虽然对真实解提供了一个严格的上限,但上限法中采用相关联流动法则，过大地考虑了土的剪胀性。

有限元法由于能反映边坡岩土体的应力-应变关系，考虑实际边坡体的复杂边界条件和采用一般土的材料模型，因而是一种较好的研究边坡稳定性的方法。

1.强度折减原理
在有限元静力稳态计算中,如果模型为不稳定状态,有限元计算将不收敛。

那么反过来,通过调整参数,使有限元计算从收敛变得不收敛,就表征边坡模型从稳
定状态向不稳定状态发生了转变。

求解边坡稳定安全系数两种方法的比较摘要：目前，边坡稳定性分析主要有刚体极限平衡法和有限元强度折减法，本文就理论基础、安全系数的定义及优缺点对以上两种方法进行了简要评述。

基于极限平衡法的发展起来的各种方法物理意义简单，便于计算，但是需要许多假设。

有限元强度折减法不需要假设，可以直接搜索临界滑动面并求出相应的安全系数，同时考虑了岩土体的弹塑性和边坡的破坏失稳过程。

通过对两种方法的认识比较，给岩土边坡工作者设计施工提供一定的参考价值。

关键词：边坡稳定性；极限平衡法；有限元法；安全系数引言边坡稳定分析是一个非常复杂的问题，从20世纪50年代以来，许多专家学者致力于这一研究，因此边坡稳定分析的内容十分丰富。

总体上来说，边坡稳定分析方法可分为两大类：定性分析方法和定量分析方法。

定性分析方法主要是通过工程地质勘探，可以综合考虑影响边坡稳定性的多种因素，对边坡岩土体的性质及演化史、影响边坡稳定性的主要因素、可能的变形破坏方式及失稳的力学机制等进行分析，从而给出边坡稳定性评价的定性说明和解释。

然而，人们更关心的是如何定量表示边坡的稳定性，即边坡稳定性分析的计算方法，定量方法将影响边坡稳定的各种因素都作为确定的量来考虑，通常以计算稳定安全系数为基础。

边坡稳定分析的定量方法有很多种，如条分法、数值分析方法、可靠度方法和模糊数学方法等[1-3]。

目前，边坡稳定分析方法中，人们较为熟知且广泛应用的有条分法和有限元方法。

条分法在边坡稳定分析中最早使用，因其力学模型概念清楚、简单实用，故广泛应用于实际工程中，已经逐渐成为边坡稳定分析的成熟方法。

随着计算机技术的发展，数值分析方法在工程领域应用越来越成熟，有限元方法考虑了土体的非线性应力－应变关系，同时弥补了条分法的不足，近年来有限元方法得到了极大的发展。

[4-6]刚体极限平衡法刚体极限平衡法是人们提出的最早的一类方法，是边坡分析的经典方法，只需要少许力学参数就能提供便于设计应用的稳定性指标即安全系数。

有限元强度折减法在土坡与岩坡中的应用
有限元强度折减法当今备受瞩目，因它在土坡与岩坡中的应用受到广大人士的欢迎。

它拥有准确性、节省时间、方便使用等优点，但又并不会降低土坡与岩坡的安全性和可靠性。

有限元强度折减法由受力分析开始，根据力学模型计算出受力的工况。

进一步的，通过建立模型，预测出结构的屈服情况，以及各个构件的受力情况。

有限元强度折减法此时正式开始，强度折减前先对整个模型进行极限状态分析，根据极限状态分析结果，对每一个单元进行强度折减，折减强度及方式在此时确定，最后，通过受力分析计算，计算受力是否已足够说明安全性。

有限元强度折减法在实际应用中均取得较佳的效果，尤以土坡与岩坡的应用为典型。

由于储量的不足，常常会出现一些开采后的构件结构非但不坚固，而且结构不平衡，缺乏内在的可延续性，在此情况下，有限元强度折减法的应用大有裨益。

例如可以快速确定土坡与岩坡的最优构筑方式，减少岩体开采对施工效率的影响，有效改善构筑物稳定性，提高土坡与岩坡的安全性。

有限元强度折减法虽然有效，但也不可推而广之，还是要从实际情况出发，调整它的应用模式，做到结合工程实际，准确把握性和安全性，在开发业务中扮演重要角色。

总之，有限元强度折减法在土坡与岩坡的应用引起了广大科学家的共鸣，它的准确性、节省时间、方便使用以及提高安全性等特点，都得到了广泛认可。