湖北工业大学高斯光束[可修改版ppt]

qM
AqM B 1 CqM D qM
D Ai 2B
1 (D A)2 4 B
§3.2 高斯光束与球面谐振腔的自再现模式
1 D A 1 (D A)2 4
i
qM 2B
B
1 q(z)
1 R(z)
i
2 (z)
R(z) 2B (D A)
(z) (
)1 2
B12
1
D
2
A
2
2
0 (z)
z
R(z
)
1
1
2(z) R(z)
R(z) 2
2
(
z
)
§3.1 基模高斯光束
3）基模高斯光束的特征参数：
➢ 用q参数表征高斯光束
u00
(
x
,
y
,
z
)
c00
0 (z
)
exp[
x2
2(
y2 z)
]exp{
i[k
(
z
x2 y2 ) arctg 2R(z)
1 11
q2 q1 F
q2
Aq1 Cq1
B D
复曲率半径q
§3.1 基模高斯光束
出射光束的束腰位置和尺寸： 入射高斯光束的光腰在l处， 出射高斯光束的光腰在l ’处
q q0
if
02
q
q0
if
02
等和式实两部端对的应虚相部等
f l
(l
F2 f F )2
l(l F ) f (l F )2 f
z f
]}
u00 ( x,
y, z) c00
0 exp{ik (z)
x2

p
'(
z)


i q(z)
r 0项系数
– 该式称为类透镜介质中的简化的波动方程。
5.0 （继续)类透镜介质中的波动方程
• 从麦克斯韦方程组出发，推导出各向同性、无电荷分布介质中的波动
方程为：
u 2E 2E
t 2
• 若假设其解为修正平面波，且将类透镜介质折射率表达式带入其中可
以得到： 2 2ik ' kk 2r2 0 • 其中 (x, y, z) 为修正因子，若假设其形式为：

20
将上述参数带入到光场的表达式， 整理可以得到光场的表达式： E(x, y, z)
(x, y, z)e ikz

E0
0 (z)
exp
i
kz
(z)

i
kr 2 2q(z)


E0
0 (z)
exp
i
kz
(z)

r
2


20
E(x, y, z)

E0
0 (z)
exp



r2
2( z)

exp

i
kz
(z)

kr2 2R( z)

•该式所表示的是均匀介质中波动方程的一个解，称为基本高斯光束解， 其横向依赖关系只包含r，而与方位角无关。那些与方位角相关的分布是 高阶高斯光束解。
波动方程 也称亥姆 霍兹方程
波动方程
2E0 k 2(r)E0 0
k 2(r) 2u (r)
波动方程 也称亥姆 霍兹方程

exp ix,
y, z
二、基模振幅分布和光斑尺寸
1、振幅分布
对基横模TEM00
U 00
Cmn
exp
1
2
2
x2 y2
s2
基横模TEM00的光强
I 00
U
2 00
Cm2 n
exp
1
4
2
x2 y2
s2
——基模截面是高斯函数
2、光斑尺寸振幅下降为最大值1/e时的光斑半径
2z L
(z) s
2
1 2 s
在横截面内的场振幅分布按高斯函数所描述的规律从 中心(即传输轴线)向外平滑地降落。
花样：沿x方向有m条节线，沿y方向有n条节线。
2 exp ix, y, z ：位相因子，决定了共焦腔的位相分布
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
yexp12 2x2 y2 ws2
由于透射、散射和吸收等因素而产生的损耗；δd为激光在谐振腔中因衍射
而产生的损耗。
因此，选横模的实质是使需要的横模（一般为基模TEM00）满足阈值条 件产生振荡，而使不需要的横模（一般为高阶模）不满足阈值条件而被抑 制，从而达到滤去高阶模的目的。由于G、δi、δm对不同横模来说是相 同的，因而满足振荡阈值条件主要由衍射损耗δd来决定。为了达到上述目 的，应当尽量减小δi和δm，或相对增长δd，使得腔的总损耗a中衍射损 耗δd能起决定作用，因而有利于选模。
L
镜面有效截面半径
3、 (z在) 纵截面上的表达式
( 0
z)
1 2
L [1 2 s
(

§3.1 基模高斯光束
高斯光束在其传输轴线附近 可近似看作是一种非均匀球面波 曲率中心随着传输过程而不断改变 振幅和强度在横截面内始终保持高斯分布特性 等相位面始终保持为球面 强度集中在轴线及其附近
§3.1 基模高斯光束
3）基模高斯光束的特征参数： ➢ 用参数0（或f）及束腰位置表征高斯光束
f
2 2
2 F
q
(1
l F
)q (l q (1
l l
)
ll F
)
F
F
0
(l
F F )2
f
2 0
§3.1 基模高斯光束
出射光束的束腰位置和尺寸 随入射光束的变化：
l
l(l F ) (l F )2
f f
2 2
F
0
(l
F F )2
f
2 0
§3.1 基模高斯光束
0
(l
第三章 高斯光束及其特性
本章大纲
§3.1 基模高斯光束 掌握高斯光束q参数的表达 高斯光束在线性光学系统中的变换 高斯光束的自再现变换与稳定球面腔模式的关系
§3.2 高阶高斯光束 了解高阶高斯光束的特性。
§3.3 高斯光束的准直与聚焦 了解高斯光束的准直的与聚焦特点。
§3.1 基模高斯光束
1）沿z轴方向传播的基模高斯光束
z f
]}
u00 ( x,
y, z) c00
0 exp{ik (z)
x2
2
y2 1
[ R(z) i 2(z)]}exp[i(kz arctg
z f
)]
引入一个新的参数q(z)，定义为
11
q(z)
R( z )

激光原理与技术·原理部分
第5讲 高斯光束---激光器基本光束
重复5.4 波动方程=数学基础+物理概念
• 类透镜介质中的波动方程---博士生考试
– 在各向同性、无电荷分布的介质中，Maxwell方程组的微分形式为：

H


E t
(1)
对2式求旋度：
E u H u 2E


E0
exp
i

p(z)

k 2q(z)
r2

• 可得到简化的波动方程：

1 q(z)
2


1 q(z)

'

k2 k

0

p
'(
z)


i q(z)
5.1 均匀介质中的高斯光束
– 均匀介质可以认为是类透镜介质的一种特例，即k2=0时的类透镜介质，此时简化 波动方程为：
t
t 2
E E 2E 且由3式：


E

u
H t
(2)
E 0
(3)


E E E 0 E 1 E

在各向同性介质中有介电常数不随位置而发生变化，即
的瑞利长度，通常记作 f 。
在实际应用中，一般认为基模高斯光束在瑞利长度范围内是近似平行的，因此也
把瑞利距离长度称为准直距离。从瑞利长度表达式
z
0


2 0

/

可以得
出结论，高斯光束的束腰半径越大，其准直距离越长，准直性越好。

ω（ｚ）为ｚ 点处的光斑半径，它是距离ｚ 的函数，即
槡 （ ） ω（ｚ）＝ω０
１＋
λｚ πω２０
２
（４５）
·８３·
ω０ 是ｚ＝０处的ω（ｚ）值，即高斯光束的“束腰”半径。
式（４４）中 Ｒ（ｚ）是在ｚ 点处波阵面的曲率半径，它也是ｚ 的函数，即
［ （ ）］ Ｒ（ｚ）＝ｚ １＋
πω２０ λｚ
２
φ（ｚ）是与ｚ 有关的位相因子，且
当ｚ 趋向无穷大时（ｚ→∞），高斯光束的发散角 即 为 双 曲 线 两 条 渐 近 线 之 间 的 夹 角，将 其
定义为高斯激光束的远场发散角，通常用θ０ 来表示，即
θ０＝ｌｚｉ→ｍ∞２ωｚ（ｚ）＝π２ωλ０
（４１１）
如图４５所示。
图４４ 高斯光束等相位面的分布示意图
图４５ 高斯光束的发散角
理论计算表明，基模高斯光束的发散角具有毫弧度的数量级，因此其方向性相当好。由于
高阶模的发散角是随模阶次而增大，所以多模振荡时，光束的方向性要比单基模振荡差。
４ 瑞利长度 若在ｚ＝ｚＲ 处，高斯光束光斑面积为束腰处最小光斑面积的两倍，则从束腰处算起的这个 长度ｚＲ 称为瑞利长度，如图４６所示。
在瑞利长度ｚＲ 位置处，其光斑半径ω（ｚＲ）为腰斑半径ω０ 的槡２倍，即
１ ｑ（ｚ）
因此，ｑ参数也可以用来表征高斯光束。
将式（４４）改写为如下形式
（４１５）
｛ ［ （ ）］ ｝ Ｅ（ｘ，ｙ，ｚ）＝ωＡ（ｚ０）ｅｘｐ －ｉｋ ｚ＋ｘ２２＋ｙ２ Ｒ１（ｚ）－ｋω２２ｉ（ｚ） ＋ｉφ（ｚ）
将式（４１４）代入上式得
｛ ［ ］ ｝ Ｅ（ｘ，ｙ，ｚ）＝ωＡ（ｚ０）ｅｘｐ －ｉｋ ｚ＋ｘ２ｑ２＋（ｚｙ）２ ＋ｉφ（ｚ）

13
5.2 类透镜介质中的高斯光束
类透镜介质中k2 0，此时的简化波动方程为：
2 k 1 1 2 0 q z q z k i p z q z
S z 1 仍引入函数S z ： ，可以得到： q z S z
2 k 1 1 2 0 q z q z k 可得到简化的波动方程： i p z q z
2
5.1 均匀介质中的高斯光束
均匀介质可以认为是类透镜介质的一种特例，即k2 0时的类透镜介质， 此时简化波动方程为：
Johann Carl Friedrich Gauss (1777 ?
0 r2 E E0 exp 2 z z
8
5.1 均匀介质中的高斯光束
高斯光束基本特性
振幅分布特性
0 r2 exp 2 由高斯光束的表达式可以得到： E E0 z z
5.1 均匀介质中的高斯光束
E x, y, z
上面最后一个表达式中的两项，前一项是振幅项，后一项是相位项。
为什么是这个解？还有其他解吗？
7
5.1 均匀介质中的高斯光束
高斯分布：
在统计学中更多的被称为正态分布， 它指的是服从以下概率密度函数的分布：
2 x 1 f x, , exp 2 2 2
1/ e
2
Z
Z
即光束半径随传输距离的变化规律 为双曲线，在z 0时有最小值0 ， 这个位置被称为高斯光束的束腰位置。
9
5.1 均匀介质中的高斯光束
等相位面特性

它包含了相位和振幅修正两部分。
• 该修正因子满足慢变近似：'k,"k2 将这些相
关假设带入波动方程可以得到：
2 2 ik'kk2 r20
波动方程
• 令修正因子取以下形式：
E0exp ip(z)2qk(z)r2
为什么取这种形式？这是对波动方程进行长期研究得到 的解，既满足方程，又有明确的、能够被实验证实的物 理意义。
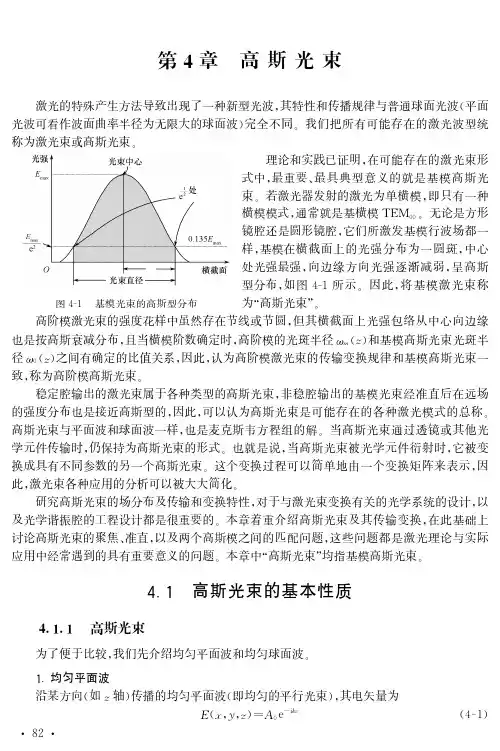
长度之外，高斯光束迅速发散，定义当 z时高斯光束振幅减小到
最大值1/e处与z轴夹角为高斯光束的远场发散角（半角）： – （下一页推导）
lim(z) z z 0 z0
– 包含在全远场发散角内的光束功率占 高斯光束总功率的86.5%
2(z)
20
1
z 20
2
20
1
z2 z20
z0
2 2 r z22 r2 21 r r z22
波动方程
• 我们假设 2 ，其中a为集中大部分能量的横截面半
径，这一假设说明衍射效应很弱，因此可以将推导局限于 单一的横向场分量，其单色平面波的表达式为：
E(x,y,z)eikz
其中e-ikz表示波数为k的严格平面波；
• 为了研究修正平面波，我们引入了修正因子 (x, y, z) ，
2
y
H
n
y
• (x, y, z) 仍为基本高斯光束解，所以总的解为
El,m(x,y,z)E0(0 z)Hm 2(xz)Hn 2(yz)
H 0(x) 1 H 1(x) 2x H 2(x) 4x2 2 H 3(x) 8x3 12x
exp x22(zy)2ik(2 xR 2 (zy)2)kz(mn1)(z)
ω/2

把瑞利距离长度称为准直距离。从瑞利长度表达式 z020/ 可以得
出结论，高斯光束的束腰半径越大，其准直距离越长，准直性越好。
5.1 均匀介质中的高斯光束
• 高斯光束的孔径
– 从基模高斯光束的光束半径表达式可以得到截面上振幅的分布为：
–
则其光强分布为：
I(r)
I0exp2r22
A(r)
A0expr22
20
lim(z) z z 0 z0
• 高斯光束在轴线附近可以看成一种非均匀高斯球面 波，在传播过程中曲率中心不断改变，其振幅在横 截面内为一高斯分布，强度集中在轴线及其附近， 且等相位面保持球面。
5.3 均匀介质中的高阶高斯光束
• 前面推导均匀介质中的基模高斯光束解时曾假设振幅横向分布与方位 角无关，如果考虑方位角的变化 0 ，则算符可以表示为：
2 0
z2 z20
1
1
即光束半径随传输距离的变化规律为双曲线，在z=0时有
最小值 0 ，这个位置被称为高斯光束的束腰位置。
1/ e
Z
Z
E (x,y,z)
E 0 (z 0)exp 2 r(2 z) exp相 位 移 i kz(z)2R kr(2 z)
总 相 位 移 ( x ,y ,z ) k z ( z ) 2 R k r ( 2 z ) k z 2 R r ( 2 z ) t a n 1 z 2 0
该表达式就是类透镜介质 的折射率表达式，证明我 们考虑的k(r)表达式代表
级数 展开
2 k0 12 kk20r2 n0 12 kk20r2
的正是在类透镜介质中的 情况。
波动方程
• 类透镜介质中波动方程的解，考虑在介质中传播的是一种 近似平面波，即能量集中在光轴附近，沿光轴方向传播。

– 在实验上和理论上都证实了工作物质的折射率随温度发生变化：
(x,
y)
0(T 0)
n T
D 4K
(x2
y2)
– 可见工作状态下的Nd：YAG工作物质是一种二次折射率介质。
21
2.1光线的传播
• 3. 光线在均匀和非均匀各向同性介质中的传播
–
程函(eikonal)方程：
x
2
y
2
x y
0 0
d 2r dz 2
k k
2 0
r
0
23
2.1光线的传播
–
（1）k2>0
微分方程的解为 r(z) c1cos
k k
2 0
z
c
2
sin
k k
2 0
z
若考虑光线入射初始条件
为
r0
r
0
'
，则可以求出
c1
r 0; c2
k，因此微分方程的解可以写成：
r
z
r
0
cos
– 1. 薄透镜的聚焦机理
– 一单色平面波，经过薄透镜后，产生一个与离轴距离r2成正比的相位超 前量，补偿了到达焦点几何路径的不同所引起的相位不同滞后量。到达
焦点时间、相位相同，实现聚焦，此时的薄透镜相当于一个平面的相位
变换器。
AB AO BO
f 2 x2 y2 f f 1 x2 y2 f
k k
2 0
z
k k
0 2
r
'
0
sin
k k
2 0
z
r ' z
k k
2 0
r

其中：
Rzz1
zf 2z1wz022
w2(z)w021zf 2w021wz022
经整理后可得： qziw 0 2zifzq(0)z
高斯光束在自由空间由z1经距离L传播到z2,q的规律为 ：
q z 2 q z 1 z 2 z 1 q z 1 L
高斯光束的复数曲率半径与普通球面波的曲率半径遵循相同的传播规律
段时, 其波的功率很低, 应用效果不理想; 长期以 来，缺乏有效的 THz 辐射源和检测方法，人们对 于该波段的电磁辐射特性了解甚少，以至形成所 谓 “THz 空白” 的现象。
THz 波的产生方法和特点
THz 产生 方法
原理
频率范围 功率范围 优点、缺点 (THz) (平均)
固态振荡器、 晶体振荡、 二极管放大器 放大
若使一个稳定腔所产生的高斯光束与另一个稳定腔产生 的高斯相匹配，需在合适的位置放置一个焦距适当的透镜， 使两束高斯光束互为物象共轭光束。该透镜称为模匹配透镜。
高斯光束的匹配
已 的知 高物斯方光高 束斯，光求束物的距腰z斑和w像0 距，要z求/ 在，像以方及得模到匹腰配斑透为镜的w 0焦/ 距，f.
采取的方法：用高斯光束复参数q和ABCD定律推导。
透镜处物方的复参数 qf q0 z
复参数经过透镜的变换
1
q
/ f
1 qf
1 f
(q0/ z/)(q01z1f )1
像方腰斑处的复参数 q0/ q/f z/
高斯光束的匹配
f0w0w0 为特征匹配配 长光 度束 ，的 由腰 匹部直
1 i
q
w02
解 (1)
w0
f
z=0.5m
fw 0 2 3 3..1 14 4 1 10 0 6 6 1m q=0.5+i(m)

Aq1 B q2 Cq1 D
曲率半径R
复曲率半径q
例1 某高斯光束焦参数为f=1m,将焦距F=1m 的凸透镜置於其腰右方l=2m处,求经透镜变换 后的像光束的焦参数f及其腰距透镜的距离l 解 q=2+i
q f(w0)
O
q f(w0) Z
O
l F l
研究对象
普通球面波
高斯球面波
特点
曲率中心固定的 曲率中心变化的
q2=q1+L
1 1 1 q2 q1 F
在自由空间的传 R2=R1+L 输规律 通过薄透镜的变 1 1 1 R2 R1 F 换 总的变换规律 AR1 B
R2 CR1 D
高斯光束q参数的传输规律
1、传播L距离
q q L
1 T 0 L 1
证
传播L距离的光学变换矩阵
1 q L q qL 0 q 1
2、通过透镜
q、q:透镜处物、像高斯光束q参数 l、l :物、像高斯光束腰到透镜距离 f、f :物像高斯光束焦参数
1 T 1 F 0 1
• 研究对象：高斯球面波—非均匀的、曲率中心不断改变的 球面波 • q参数在自由空间的传输规律q(z)=q0+z，q2=q1+L 1 1 1 • 通过薄透镜的变换
q2
q1
F
• q参数的变换规律可统一表示为
Aq1 B q2 Cq1 D
• 结论：高斯光束经任何光学系统变换时服从ABCD公式，由 光学系统对傍轴光线的变换矩阵所决定。 • 优点：能通过任意复杂的光学系统追踪高斯光束的q参数值 (将q称为复曲率半径the complex radius of curvature)

0
L 2
R0
z
[1
(
2 0
)]
z
(z) 0
1
z
(
2 0
)2
s 20
2 2 0
第5页/共6页
0
1
(
z
2 0
)2
2
2
2 2 L 0
2.由波动光学知道，在单色平行光照 明下， 一个半 径为 r 的圆孔夫琅和费衍射角(主极大至第 一极小 值之间 的夹角 )
。与上式相比较可知．高斯光束半角远 场发散 角在数 值上等 于以腰 斑 为半径的光束的衍射角，即它已达到 了衍射 极限。
0.61 r 0
第1页/共6页
3.3.2 高斯光束的相位分布
1.
随坐标而变化，与腔的轴线相交于 点的等相位面的方程为
(x, y, z)
z0
(x, y, z) (0,0, z0)
(
x,
y,
z)
k[
L 2
(1
2z L
)
1
2z L (2z L)2
x2 y2 ] (m n 1)(
L
2
)
k
L 2
1
2z
2z L
B I SΩ
Ω (R)2 R2 2
2.一般的激光器是向着数量级约为10－6 sr的立体角范围内输出激光光束的。而 普通光 源发光( 如电灯 光)是 朝向空 间各个 可能的 方向的 ，它的 发光立 体角为4 πsr。 相比之 下，普 通光源 的发光 立体角 是激光 的约百 万倍。
3.小结一下高斯光束的主要特征参量 ：
高斯光束的振幅和强分布激光原理及应 用电子电子
会ቤተ መጻሕፍቲ ባይዱ学