一道平面几何题的证明及共改进
- 格式:pdf
- 大小:63.85 KB
- 文档页数:2

用平面几何证明三角形重心的性质
作者:王欣
来源:《都市家教·下半月》2015年第11期
人教版八年级下册课本上有这样一道关于三角形重心的题:在ABC中,BD、CE是边AC、AB上的中线,BD与CE交于点O。
BO与OD的长度有什么关系?BC边上的中线是否一定过点O?为什么?
分析:三角形三条中线的交点是三角形的重心(第十九章课题学习《重心》)。
这道习题要证明的结论是三角形重心的一个重要数学性质:三角形的重心将三角形的每条中线都分成1∶2两部分,其中重心到三角形某一顶点的距离是到该顶点对边中点距离的2倍。
点评:利用平行四边形性质和三角形中位线性质的推论得到相同的结论。
方法1、2实际上是属于截长形式的证明线段相等的方法,方法3、4、5实际上都是属于补短形式的证明线段相等的方法。
证明线段和的问题最常用的就是截长补短的方法。
教师在上课时要善于引导学生去思考而不是匆匆给出结论,把重点放在解题策略上,通过反复引导、激励,调动学生学习数学的积极性,提高学生的思维能力。
另外,教学相长,教师在课后也要及时反思,总结经验,不断改进,这样才能使课堂教学更有新意、更高效。


高中数学证明几何的题的知识点总结线面垂直线面平行点面面面的证明几何证明是高中数学中的重要组成部分,它不仅锻炼了学生的逻辑思维能力,还培养了严密的数学推理能力。
本文针对高中数学中常见的线面垂直、线面平行以及点面、面面关系证明的知识点进行总结,以帮助学生更好地掌握几何证明的技巧和方法。
一、线面垂直的证明1.定义:如果一条直线与一个平面内的任意一条直线都垂直,则这条直线与该平面垂直。
2.判定定理:如果一条直线与一个平面内的两条相交直线垂直,则这条直线与该平面垂直。
3.证明方法:(1)利用垂直的定义,找出直线与平面内任意一条直线垂直的关系。
(2)利用判定定理,找出直线与平面内两条相交直线垂直的关系。
二、线面平行的证明1.定义:如果一条直线与一个平面内的任意一条直线都没有公共点,则这条直线与该平面平行。
2.判定定理:如果一条直线与一个平面内的两条平行直线都平行,则这条直线与该平面平行。
3.证明方法:(1)利用平行的定义,找出直线与平面内任意一条直线没有公共点的关系。
(2)利用判定定理,找出直线与平面内两条平行直线都平行的关系。
三、点面关系的证明1.定义:如果一点在一个平面内,则这个点与该平面有公共点。
2.判定定理:如果一点与一个平面内的任意一条直线都有且只有一个公共点,则这个点在该平面内。
3.证明方法:(1)利用定义,找出点与平面内任意一条直线有公共点的关系。
(2)利用判定定理,找出点与平面内任意一条直线有且只有一个公共点的关系。
四、面面关系的证明1.定义:如果两个平面有公共点,则这两个平面相交。
2.判定定理:如果两个平面内分别有两条相交直线互相平行,则这两个平面平行。
3.证明方法:(1)利用定义,找出两个平面有公共点的关系。
(2)利用判定定理,找出两个平面内分别有两条相交直线互相平行的关系。
通过以上对高中数学几何证明知识点的总结,相信同学们在解决相关问题时会更加得心应手。
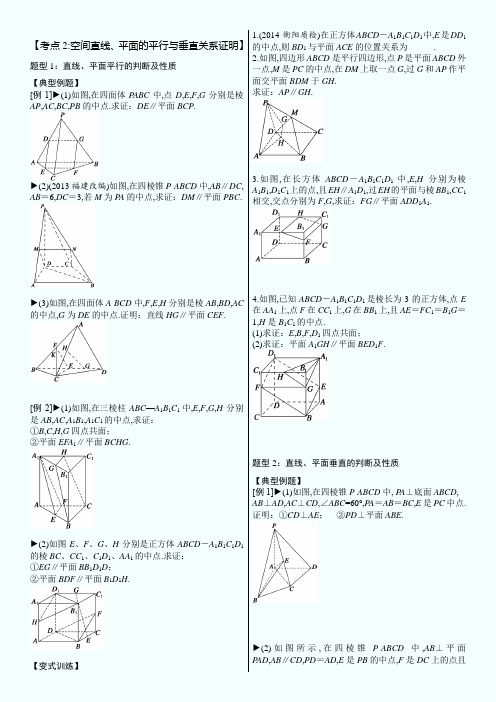
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。

在△ABC中,AB=AC,P是△ABC内部的一点,且∠APB﹥∠APC。
求证:PB<PC由于AB=AC,可将△ABP旋转至AP'C。
∵AP‘=AP,∴∠APP'=∠AP'P∵∠AP’C = ∠APB > ∠APC∴∠PP'C > ∠P'PC∴ BP=CP' < PC在△ABC中,∠C=90°,M在BC上,且BM=AC,N在AC上,且AN=MC,AM与BN相交于点P,求证:∠BPM=45°在直角三角形ABC中,∠C=90°,M在BC上,N在AC上,且BM=AC,AN=MC,求证∠BPM=45°。
证明设AC=b,BC=a, 则CM=AM=a-b,CN=2b-a。
过N点作NH∥AM,过M点作MH∥AC,交于H.连BH.则四边形ANHM是平行四边形,所以 MH=AN=CM=a-b,AM=NH.由勾股定理得:BN^2=BC^2+CN^2=a^2+(2b-a)^2=2(a^2-2ab+2b^2);AM^2=AC^2+CM^2=b^2+(a-b)^2= a^2-2ab+2b^2;BH^2=BM^2+MH^2=b^2+(a-b)^2= a^2-2ab+2b^2.所以得 AM=BH,AM^2+BH^2=BN^2。
故三角形BHN是等腰直角三角形。
因此∠BPM=∠BNH=45°。
这里的O 点相当于你们作业上的G 点 将边长为1+n/2(n=1,2,3,……)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A1A2A3,……2011-2-19 10:16提问者: 兔兔漂亮吗 | 浏览次数:1369次(1)若摆放前6个正方形纸片,则被遮盖的线段长度和为( ),(2)若摆放前n (n 为大于1的正整数)个正方形纸片,则被遮盖的线段长度之和为( )答案为:10 1/4*(n+2)(n-1)①过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,根据正方形的性质推出∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,求出∠AA 1B=∠DA A C ,证△BAA 1≌△CDA 1,得到AB=DC ,求出虚线部分的线段之和是1,依次求出其它虚线之和,相加即可;②根据①的结论求出12×(2+3+4+…+n )即可.①解:过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,∵正方形EFGH ,∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,∴∠AA 1D=∠BA 1C=90°,∴∠AA 1B=∠DA A C ,∴△BAA 1≌△CDA 1,∴AB=DC ,∴BF+FC=FA+FD=1+12=1,同理第2个虚线之和是1+22=3,同理第3个虚线之和是2,同理第4个虚线之和是5同理第5个虚线之和是3,∴1+32+2+52+3=12×(2+3+4+5+6)=10,②若摆放前n个(n为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为12×(2+3+4+…+n)=n2+n-24,故答案为:10,n2+n-24.S△DEF+S△CEF= 12S△ABC 仍然成立.证明:当∠EDF绕点D旋转到DE⊥AC于E时,连接CD.∵Rt△ABC中,AC=BC,即△ABC为等腰直角三角形.又∵D为AB边的中点,∴CD=BD,∠ECD=∠FBD=45°,∠CDB=90°,又∵∠EDF=90°,∴∠EDF-∠CDF=∠CDB-∠CDF,即∠CDE=∠BDF,∴△CDE≌△BDF,∴S△CDE=S△BDF,∴S△DEF+S△CEF=S△CDE+S△CDF=S△BDF+S△CDF=S△BCD= 12S△ABC,得证.当∠EDF绕点D旋转到DE和AC不垂直时:猜想 S△DEF+S△CEF= 1/2S△ABC,证明:连接CD,同理易得△CDE≌△BDF,∴S△CDE=S△BDF,∴S△DEF+S△CEF=S四边形DECF=S△CDE+S△CDF=S△DBF+S△CDF=S△BCD,又S△BCD= 12S△ABC,则S△DEF+S△CEF= 12S△ABC.故答案是:S△DEF+S△CEF= 12S△ABC,S△DEF+S△CEF=12S△ABC.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M 放在△ABC的斜边AB的中点处,设AC=BC=a.解:(1),(1+)a;(2),2a;(3)猜想:重叠部分的面积为。

D 几何证明题的技巧1.几何证明是平面几何中的一个重要问题,它有两种基本类型:一是平面图形的数量关系;二是有关平面图形的位置关系。
这两类问题常常可以相互转化,如证明平行关系可转化为证明角等或角互补的问题。
2.掌握分析、证明几何问题的常用方法:(1)综合法(由因导果),从已知条件出发,通过有关定义、定理、公理的应用,逐步向前推进,直到问题解决;(2)分析法(执果索因)从命题的结论考虑,推敲使其成立需要具备的条件,然后再把所需的条件看成要证的结论继续推敲,如此逐步往上逆求,直到已知事实为止;(3)分析综合法:将分析与综合法合并使用,比较起来,分析法利于思考,综合法易于表达,因此,在实际思考问题时,可合并使用,灵活处理,以利于缩短题设与结论的距离,最后达到证明目的。
3.掌握构造基本图形的方法:复杂的图形都是由基本图形组成的,因此要善于将复杂图形分解成基本图形。
在更多时候需要构造基本图形,在构造基本图形时往往需要添加辅助线,以达到集中条件、转化问题的目的。
1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
例1. 已知:如图1 所示,∆ABC 中,∠C = 90︒,AC =BC,AD =DB,AE =CF 。
求证:DE=DF AEC F B图1分析:由∆ABC 是等腰直角三角形可知,∠A =∠B = 45︒,由D 是AB 中点,可考虑连结CD,易得CD =AD ,∠DCF = 45︒。
从而不难发现∆DCF ≅∆DAE证明:连结CDAC =BC∴∠A =∠B∠ACB = 90︒,AD =DB∴CD =BD =AD,∠DCB =∠B =∠AAE =CF,∠A =∠DCB,AD =CD∴∆ADE ≅∆CDF∴DE =DF说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中EF2 3 1线或高是常用的辅助线。
【例23】如图,已知等腰直角三角形ABC ,BD 平分ABC ∠,CE BD ⊥,垂足为E ,求证:2BD CE =.B AEDC【解析】解法一:如图,延长BA 、CE 于F .B AEDCF∵FBE CBE ∠=∠,BE CF ⊥,∴12CE EF CF ==.∵90FCA F ∠+∠=︒,90DBA F ∠+∠=︒, ∴FCA DBA ∠=∠.又∵AC AB =,90FAC DAB ∠=∠=︒, ∴FCA DBA ∆∆≌, ∴CF BD =. ∵2CF CE =, ∴2BD CE =.解法二:如图,作ACB ∠的平分线CF ,则CF BD =.过D 作DH CF ⊥,垂足为H ,连接FD .BA HFEDC∵ABC ACB ∠=∠,∴BD CF =,BF CD =, ∴FD BC ∥.∴45AFD ABC ∠=∠=︒,122.52DFC BCF ACB ∠=∠=∠=︒.∴DFC DCF ∠=∠,故DF DC =. ∴DH 是CF 的中垂线,∴1122HC HF CF BD ===.∵90ECD CDE ∠+∠=︒,90ABD ADB ∠+∠=︒,CDE ADB ∠=∠, ∴22.5ECD ABD ∠=∠=︒, ∴ECD HCD ∠=∠.又∵90DEC DHC ∠=∠=︒,DC 公共, ∴DCE DHC ∆∆≌,∴12CE HC BD ==,即2BD CE =.解法三:如图,过D 作DH BC ∥交AB 于H .过H 作HF BD ⊥,垂足为F .BA EDC HF∴45AHD ABC ∠=∠=︒,HDB DBC HBD ∠=∠=∠, ∴HB HD =.∴HF 是BD 的中垂线,∴12F BD =.又∵AH AD =,AB AC =,∴HB CD =.∵BHF BDA CDE ∠=∠=∠,∴Rt Rt BFH CED ∆∆≌.∴BF CE =,12CE BD =,即2BD CE =.解法四:如图,作BD 的中垂线GH 交BC 于H ,则BH DH =,HDG HBG ∠=∠.C DEABGH而ABG HBG ∠=∠,∴HDG ABG ∠=∠,从而HD AB ∥. ∴45DHC ABC ∠=∠=︒, ∴HD CD =,即BH CD =.又∵90ECD CDE ∠+∠=︒,90ABD ADB ∠+∠=︒,ADB CDE ∠=∠. ∴ECD ABD ∠=∠,即ECD GBH ∠=∠. ∴Rt Rt CED BGH ∆∆≌.∴12CE BG BD ==,故2BD CE =.解法五:如图,取BD 的中点F ,连接AF 、AE .FBAE D C∵AF 是Rt ABD ∆斜边上的中线,∴12AF BF BD ==,245AFE ABF BAF ABF ABC ∠=∠+∠=∠=∠=︒.∵AB AC ⊥,CE BE ⊥,∴90BAC BEC ∠=∠=︒, ∴A 、B 、C 、E 4点共圆.∴45AEB ACB ∠=∠=︒,∴AF AE =. 又∵ABE EBC ∠=∠,∴AE CE =.即12CE BD =,∴2BD CE =.解法六:如图,作BC 的中线AM ,则A M B C ⊥,AM 平分BAC ∠,取CD 的中点F ,连接MF 、ME ,则12MF BD =.CDE ABFM∵ME 是Rt BCE ∆斜边上的中线,∴ME BM =,∴122.52MEB DBM ABC ∠=∠=∠=︒,∴45CME MEB DBM ∠=∠+∠=︒, ∴45CME MAF ∠=∠=︒.又∵90ECB CBE ∠+∠=︒,90ADB ABD ∠+∠=︒,CBE ABD ∠=∠, ∴ECB ADB ∠=∠.∵MF BD ∥,∴MFA ADB ∠=∠.即MFA ECB ∠=∠. ∴AMF MEC ∆∆≌,∴MF CE =,即12CE BD =,故2BD CE =.。
通过一道题目看三点共线问题的常用证明方法(陕西师范大学附中 张锦川 王全 710061)题目:如图,已知AB 是半圆O 的直径,,CA CD 是该半圆的切线,,A D 为切点,DE 垂直AB 于点E ,且F 为DE 中点,求证:,,B F C 三点共线.三点共线是平面几何中的典型问题,证法灵活多样,对于学生逻辑思维的锻炼及几何感觉的培养大有裨益.常见的证明方法有:利用角的关系证明、利用梅涅劳斯定理的逆定理证明、利用塞瓦定理的逆定理证明、利用向量共线证明、利用解析法证明、利用同一法证明等.下面,笔者拟使用这些方法对本题进行证明:思路一、利用角的关系证明:解法1:通过证EBF ABC ∠=∠来证点,,B F C 共线.证明:连接,,,OC OD AD BD ,由已知可得OC AD ⊥,又BD AD ⊥,∴ OC ∥BD , 易知OACBED ∆∆,则AC ED OA BE =,即212AC EFBE AB =. 故AC EFAB BE=,即tan tan ABC EBF ∠=∠, 从而可得ABC EBF ∠=∠,故点,,B F C 共线.思路二、利用梅涅劳斯定理的逆定理证明:解法2:通过梅涅劳斯定理的逆定理证点,,B F H 共线来证明点,,B F C 共线.证明:同解法1得AC EF AB EB=,即EF AB BE AC ⋅=⋅. 故1DH AB EF DH AB DF AB EF ABHA BE FD HA BE AC BE BE AC⋅⋅=⋅=⋅=⋅=. 故点,,B F H 共线,从而可得点,,B F C 共线.FED OABCCF EOABDH CF EOABD解法3:由切线的性质得线段的关系后结合梅涅劳斯定理的逆定理证点,,B F C 共线. 证明:作BQ PD ⊥于点Q ,则由PD 为切线可知PDB BAD BDE ∠=∠=∠,故有BQ BE =.由PBQPCA ∆∆得BQ CA CDBP CP CP==. 于是有1PC DF EB BP DF EBCD FE BP BQ FE BP⋅⋅=⋅⋅=. 所以,由梅涅劳斯定理的逆定理可得点,,B F C 共线.解法4:由调和点列的相关知识与梅涅劳斯定理的逆定理直接证明点,,B F C 共线. 证明:由于AB 为直径,DE AB ⊥,以及PD 为切线可知:点,,,P A B E 成调和点列,即PA AEPB BE=. 又因DE ∥AC ,故PC PACD AE=. 因此有1PC DF EB PA BE CD FE BP AE PB⋅⋅=⋅=,于是由梅涅劳斯定理的逆定理可得点,,B F C 共线.注:利用梅涅劳斯定理的逆定理证明时,选择不同的三角形会得到不同的比式乘积.因而要挖掘题目的条件,选准方向进行求证.思路三、利用塞瓦定理的逆定理证明:解法5:由赛瓦定理的逆定理证点,,B F H 共线来证明点,,B F C 共线.证明:同解法1得DH DF EF BEAH AC AC AB===. 又由DF EF =可得A D F A E F S S ∆∆=,即sin sin DAF AEEAF AD∠=∠. 于是有sin sin ADG ABG S DG AD DAG AD AE AEBG S AB BAG AB AD AB∆∆∠===⋅=∠. 故1DG BE AH AE BE AB GB EA HD AB AE BE⋅⋅=⋅⋅=. 所以,由赛瓦定理的逆定理可得点,,B F C 共线.GH CFEOABD PCF EOABDQ PCFEOABD思路四、利用向量共线证明:解法6:可以利用向量共线的方法证明CF BF ∥. 证明:设AE AB λ=,EF AC μ=.∴ (1)CF CA AE EF AB AC λμ=++=+-; (1)BF BE EF AB AC λμ=+=-+. ∵ 向量AB 、AC 可以作平面内一组基底,∴ 点,,B F C 共线CF BF ⇔∥(1)(1)1λμλμλμ⇔=--⇔+=. 下面证明1λμ+=.(21)CD CA AE ED AB AC λμ=++=+-,两边平方可得222222222||||(21)||||(44)||CD AB AC AB AC λμλμμ=+-⇔=-2222||44||AB AC μμλ-⇔=, ①又10()()0()(2)02CO AD CA AO AE ED AC AB AB AC λμ⋅=⇔+⋅+=⇔-+⋅+= 22||4||AB AC λμ⇔=22||4||AB AC μλ⇔=, ② 由①,②可知224441μμμλμλλ-=⇔+=.∴ ,,B F C 三点共线.思路五、利用解析法证明:解法7:由于本题关系明确,且图形简单,因此用解析法来证明点,,B F C 共线. 证明:如图建立平面直角坐标系,不妨设圆的半径为1,点D 的坐标为(,)m n ,221m n +=且0m >,则由题意得点,B F 坐标依次为(1,0)B ,1(,)2F m n . 又由于CD OD ⊥,故直线CD 的方程为:1()m m y x m n x n n n=--+=-+. FED OABCyxCFEOABD而直线AC 的方程为1x =-,故可得直线CD 与直线CA 的交点1(1,)mC n+-.故可得2(1)BF n k m =-,12BC m k n+=-,又由221m n +=可得BC BF k k =,因此点,,B F C 共线.解法8:利用解析法,通过三角换元进行证明证明: 如图建立平面直角坐标系,不妨设圆的半径为1,设点(cos ,sin )D θθ,则1(cos ,sin )2F θθ,(1,0)A -,(1,0)B ;直线CD :cos sin 1x y θθ+=,直线CA :1x =-.由1cos sin 11cos 1sin x x y x y θθθθ=-⎧+=⎧⎪⇒+⎨⎨=-=⎩⎪⎩,则点C 的坐标为1cos (1,)sin θθ+-. ∴ 1cos 2sin BC k θθ+=-,sin 2(cos 1)BF k θθ=-.易知BC BF k k =,∴ ,,B F C 三点共线.问题延伸:由解法8可知,如果将图在纵轴方向上进行伸缩变换,圆变成椭圆,直线CA 、CD 成为椭圆的切线,点F 仍为DE 的中点,,,B F C 三点依然共线.证明:如图,建立平面直角坐标系,不妨设半椭圆的方程为22221(,0)x y a b a b+=>,0y ≥.设点(cos ,sin )D a b θθ,则(cos ,sin )2bF a θθ,(,0)A a -,(,0)B a ;直线CD :cos sin 1x y a bθθ+=,直线CA :x a =-. 由cos sin 1(1cos )sin x y x aa b b y x a θθθθ=-⎧⎧+=⎪⎪⇒+⎨⎨=⎪⎪=-⎩⎩,则点C 的坐标为(1cos )(,)sin b a θθ+-.∴ (1cos )2sin BC b k a θθ+=-,sin 2(cos 1)BF b k a θθ=-.易知BC BF k k =,∴ ,,B F C 三点共线.yxCFEOABDy xC FEOABDCFEOABDABODlFEABOD CFEABODCFEABOD 思路六、利用同一法证明:解法9:用同一法证明直线BC 与DE 的交点就是线段DE 的中点.证明:设BC 交DE 于F ',如图,2BE BA OAF E CA CA =='. DF EF ''=212BE OACA DE ⇔=BE OA DE CA ⇔=. 由解法一可知OAC BED ∆∆,从而BE OADE CA=成立. 因此点F 与点F '为同一点,从而得点,,B F C 共线.注:由解法9可知直线CD 切半圆O 于点D 的充要条件是F 为DE 中点(椭圆上条件也是充要的).因此,如果换一个角度去看这个问题,已知圆上一点,可以作出圆上该点处的切线;已知道椭圆上一点,也可以作出椭圆上该点处的切线.特别地,对于椭圆来讲,在已知椭圆的长轴的情况下,作图方法简单易行.现举例作图如下:已知:椭圆O 的长轴为AB ,D 是椭圆上异于A 、B 的任一点. 求作:椭圆在点D 处的切线.作法:1.过点A 作直线l AB ⊥;作DE AB ⊥于E ,取DE 的中点F ; 2.作直线BF 交直线l 于点C ;3.作直线CD ,则直线CD 为所求作的切线.。