SPSS多重比较方式
- 格式:pdf
- 大小:227.91 KB
- 文档页数:5

单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组和其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表5-1所示。
表5-1 不同水稻品种百丛中稻纵卷叶螟幼虫数从复水稻品种1 2 3 4 51 41 33 38 37 312 39 37 35 39 343 40 35 35 38 34数据保存在“DATA5-1.SAV”文件中,变量格式如图5-1。
图5-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图5-1所示。
或者打开已存在的数据文件“DATA5-1.SAV”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统打开单因素方差分析设置窗口如图5-2。
图5-2 单因素方差分析窗口3)设置分析变量因变量: 选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量: 选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图5-3所示的对话框。
该对话框用于设置均值的多项式比较。
图5-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图5-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1.1倍和第二组的均值相等。

一、可重复单因素随机区组试验设计8个小麦品种的产比试验,采用随机区组设计,3次重复,计产面积25平米,产量结果如下,进行方差分析和多重比较。
表1 小麦品比试验产量结果(公斤)4 3 10.15 3 16.86 3 11.87 3 14.18 3 14.41、打开程序把上述数据输入进去。
2、执行:分析-一般线性模型-单变量。
3、将产量放进因变量,品种和区组放进固定因子。
4、单击模型,选择设定单选框,将品种和区组放进模型中,只分析主效应。
5、在两两比较中进行多重比较,这里只用分析品种。
可以选择多种比较方法。
6、分析结果。
主体间效应的检验因变量: 产量源III 型平方和df 均方 F Sig. 校正模型61.641a 9 6.849 4.174 .009 截距3220.167 1 3220.167 1962.448 .000 区组27.561 2 13.780 8.398 .004 品种34.080 7 4.869 2.967 .040 误差22.972 14 1.641总计3304.780 24校正的总计84.613 23a. R 方 = .729(调整 R 方 = .554)这里只须看区组和品种两行,两者均达到显著水平,说明土壤肥力和品种均影响产量结果。
下面是多重比较,只有方差分析达到显著差异才进行多重比较。
二、两因素可重复随机区组试验设计下面是水稻品种和密度对产量的影响,采用随机区组试验设计,3次重复,品种3个水平,密度3个水平,共27个观测值。
小区计产面积20平米。
表2 水稻品种与密度产比试验1、输入数据,执行:分析-一般线性模型-单变量。
注意区组作为随机因子。
2、选择模型。
注意模型中有三者的主效和品种与密度的交互。
3、分析结果。
注意自由度的分解。
使用一个误差(0.486)计算F值。
主体间效应的检验因变量: 产量源III 型平方和df 均方 F Sig. 截距假设1496.333 1 1496.333 1035.923 .0014、语句。

方差分析之多重比较目前对于均数的多重比较的方法较多,例如SPSS软件共提供18种均数的多重比较的方法。
对于均数多重比较,当资料满足正态性方差齐性时,可采用的比较方法有LSD法、Bonferroni法、Sidak法、Scheffe法、R-E-G-W F法、R-E-G-W Q法、S-N-K法、Tukey法、Tukey-b法、Duncan法、Hochberg GT2法、Gabriel法、Waller Duncan法、Dunnett法;当资料满足正态性但不符合方差齐性时,可采用Tamhane T2法、Dunnett T3、Games-Howell法、Dunnett C法。
1.常见的多重比较方法介绍1.1 LSD法原理:LSD与独立样本t检验非常相近,主要差别在于LSD法在首先满足F检验达到显著的基础上,将F检验的误差均方作为合并方差。
优点:在ANOVA中F检验显著时,LSD方法是检验效率最高的多重比较方法.缺点:①涉及过多的要比较均数对;②犯I型错误的概率较高;③这种方法只控制了每次比较犯I型错误概率,没有对总犯I型错误概率进行控制。
1.2 Bonferroni法原理:利用Bonferroni不等式来控制多次比较的总I型错误,Bonferroni不等式是指一个或多个事件发生的总概率不高于这些事件各自发生概率的加和。
通过将每次检验的α设置为总α除以检验次数,从而控制总α。
优点:用途最广,几乎可用于任何多重比较的情形,包括组间例数相等或不等、成对两两比较或综合多重比较等。
缺点:会增加犯Ⅱ型错误的概率。
1.3 Sidak法原理:基本思路与Bonferroni法接近,只是在调整仅值时采用不同的策略。
若控制单次比较犯I型错误的概率为αpc,一次比较不犯I型错误的概率为1-αpc,n次比较均不犯I型错误的概率为(1-αpc)n,则n次比较总的犯I型错误的概率为1-(1-αpc)n。
优点:调整多重比较的显著性水平,提供比Bonferroni 更严密的边界。
多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程,检验不同水平组合之间因变量均数,由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用,也可以分析因素之间的交互作用,以及分析协方差,以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来,且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量,协变量与因变量不彼此独立。
因素变量是分类变量,可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
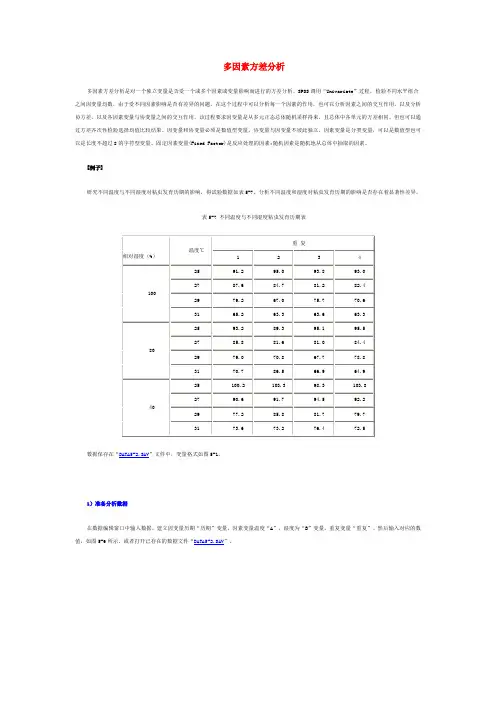
[例子]研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表数据保存在“DATA5-2.SAV”文件中,变量格式如图5-1。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量,因素变量温度“A”,湿度为“B”变量,重复变量“重复”。
然后输入对应的数值,如图5-6所示。
或者打开已存在的数据文件“DATA5-2.SAV”。
图5-6 数据输入格式2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“General Linear Model”项,在右拉式菜单中点击“Univariate”项,系统打开单因变量多因素方差分析设置窗口如图5-7。
图5-7 多因素方差分析窗口3)设置分析变量设置因变量:在左边变量列表中选“历期”,用向右拉按钮选入到“Dependent Variable:”框中。
设置因素变量:在左边变量列表中选“a”和“b”变量,用向右拉按钮移到“Fixed Factor(s):”框中。
可以选择多个因素变量。


概念笔记Main effect 一个因素的独立效应,即其不同水平引起的方差变异。
三因素的实验有三个主效应。
把某一因素的一个水平同该因素的其他水平比较,不考虑其他因素。
Interaction 多个因素的联合效应,A因素的作用受到B因素的影响,即有交互——two-way interaction. 当一因素作用受到另外两个因素影响,即三因素交互three-way interaction.重复测量一个因素的三因素混合设计3*2*2的混合设计A3*B2*R2 【A, B为被试间因素】需要分析的有——A, B, R 各自主效应二重交互作用,A*B, A*R, B*R三重交互作用,A*B*C结果发现,A, B为被试间因素,交互作用SIG当二重交互作用SIG,需要进行simple effect检验。
A因素水平在B因素某一水平上的变异。
A在B1水平上的简单效应A在B2水平上的简单效应B在A1水平上的简单效应B在A2水平上的简单效应B在A3水平上的简单效应如果三重交互作用SIG,需要进行三因素的简单简单效应分析simple simple effect. 某一因素的水平在另外两个因素的水平结合上的效应在A1B1水平结合上,R1 与R2 差异在A1B2水平结合上,R1 与R2 差异在A2B1水平结合上,R1 与R2 差异在A2B2水平结合上,R1 与R2 差异在A3B1水平结合上,R1 与R2 差异在A3B2水平结合上,R1 与R2 差异重复测量方差分析之后,如果三重交互作用显著,需要编辑语法,得出三个因素各自的简单效应某一因素在其他两个因素的某一实验条件内的简单效应检验三因素重复测量方差分析对应的会有3种简单效应检验结果SPSS在输出简单效应检验结果的同时,也会报告多重比较结果,会有更直观的对比结果。
如果三重交互作用SIG,需要进行简单简单效应检验。
固定某两个因素水平组合,考察研究者最感兴趣的那个变量的效应。
MANOV A R1 R2 BY A(1,3) B(1,2)/WSFACTORS=R(2)/PRINT=CELLINFO(MEANS)/WSDESIGN/DESIGN/WSDESIGN=R/DESIGN=MWITHIN B(1) WITHIN A(1)MWITHIN B(2) WITHIN A(1)MWITHIN B(1) WITHIN A(2)MWITHIN B(2) WITHIN A(2)MWITHIN B(1) WITHIN A(3)MWITHIN B(2) WITHIN A(3)上述语法内容是检验被试内变量R在被试间变量A, B 上的简单简单效应。
SPSS统计策略(12):多组率、构成⽐⽐较的统计⽅法(卡⽅和Fisher法)多组率、构成⽐⽐较的统计分析从第11⽂开始,介绍实验性分类数据结局的统计分析⽅法。
第11⽂介绍了两组⼆分类结局的⽐较,即两组率的⽐较,俗称四格表资料的统计分析。
分类数据除了2*2的交叉表之外,还有诸多其他形式,⽐如多组率的⽐较、2组构成⽐的⽐较、甚⾄多组构成⽐的⽐较。
它们数据结构更为复杂,虽都采⽤卡⽅检验为主要⽅法,但细节⽅⾯与两组率的分析上有所区别。
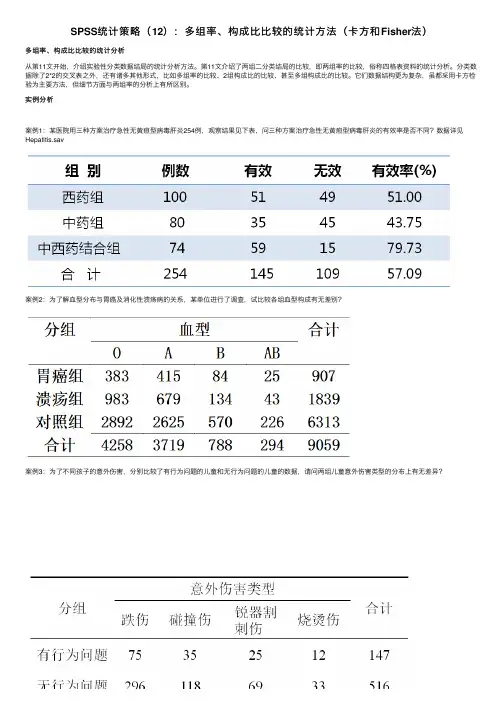
实例分析案例1:某医院⽤三种⽅案治疗急性⽆黄疸型病毒肝炎254例,观察结果见下表,问三种⽅案治疗急性⽆黄疸型病毒肝炎的有效率是否不同?数据详见Hepatitis.sav案例2:为了解⾎型分布与胃癌及消化性溃疡病的关系,某单位进⾏了调查,试⽐较各组⾎型构成有⽆差别?案例3:为了不同孩⼦的意外伤害,分别⽐较了有⾏为问题的⼉童和⽆⾏为问题的⼉童的数据,请问两组⼉童意外伤害类型的分布上有⽆差异?1案情分析案例1结局为⼆上述3个例⼦结局均为分类数据(效果、⾎型、意外伤害类型),汇总数据形成的三线表称为多⾏多列交叉表或者⾏列表多⾏多列交叉表或者⾏列表。
区别就在于,案例组多分类结局。
因此,第1个例⼦为多个率的⽐较,第2个例⼦为多个构成⽐的⽐较,第3个例⼦则是2个构分类结局,案例2为多分类结局,案例3则是2组多分类结局。
成⽐的⽐较。
2统计分析策略多⾏多列交叉表数据的分析,或者说多个率、构成⽐,乃⾄两个构成⽐的⽐较,四格表资料的分析策略⼀样,均可以考虑卡⽅和均可以考虑卡⽅和Fisher确切概率⽅法进⾏。
但是细节⽅⾯,与四格表资料的分析策略有所不同。
第⼀,多⾏多列交叉表分析没有校正卡⽅。
具体应⽤条件如下:1.不超过20%单元格的理论频数(期望频数)T < 5时,可使⽤卡⽅检验进⾏⽐较。
不超过20%的T < 5,卡⽅检验2.如果超过20%单元格的理论频数(期望频数)T < 5,或者⾄少⼀个T<1,此时采⽤的是Fisher确切概率法。



多重比较中字母标注方法
显著性检验:采用SPSS或其它数据统计软件进行,得到任意两个平均值间的显著性关系。
字母标注:
1. 首先将所有平均值由大到小排序。
2. 在最大的平均值后标字母a;
3. 以最大的平均值与居于第二的平均值对比,如显著,则标字母b(即不同字母),不显著,标字母a(即相同字母);
4. 当标不同字母时,再以标有不同字母的平均值为标准,与大于该平均值的平均值从小到大依次比较,差异不显著者标相同字母,到所有不显著的平均值中最大者时停止(即比显著者小的最大平均值);
5. 以标有相同字母的最大平均值为基础,向小的平均值变小方向比较,如差异不显著,标相同字母,差异显著,标不同字母。
当出现标不同字母时,按4中方法继续朝平均值变大方向比较。
6. 如此反复进行,直到最小的一个平均值标有字母为止。
一般地,当在0.05水平上显著时,标小写字母;当在0.01水平上显著时,标大写字母。
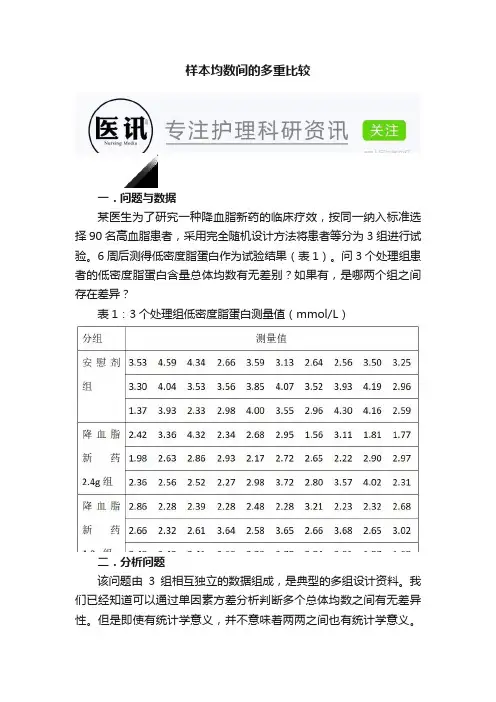
样本均数间的多重比较一.问题与数据某医生为了研究一种降血脂新药的临床疗效,按同一纳入标准选择90名高血脂患者,采用完全随机设计方法将患者等分为3组进行试验。
6周后测得低密度脂蛋白作为试验结果(表1)。
问3个处理组患者的低密度脂蛋白含量总体均数有无差别?如果有,是哪两个组之间存在差异?表1:3个处理组低密度脂蛋白测量值(mmol/L)二.分析问题该问题由3组相互独立的数据组成,是典型的多组设计资料。
我们已经知道可以通过单因素方差分析判断多个总体均数之间有无差异性。
但是即使有统计学意义,并不意味着两两之间也有统计学意义。
若想进一步判断哪两组之间存在差异,则需要做样本均数间的多重比较。
三.SPSS操作1.操作步骤将测量值放入因变量,分组放入固定因子;点击选项,勾选描述统计和齐性检验。
点击事后比较,出现如下对话框,这里,我们选择LSD、邦弗伦尼、斯达克以及邓尼特四种方法。
(LSD法最为常用)下面对最常用的LSD方法进行说明:LSD:最小显著性差异法。
用t检验完成组间成对均值的比较,检验的敏感度较高,即使各个水平间的均值存在细微差别也能被检验出来,但此方法对第Ⅰ类错误不能进行控制。
2.结果解读2.1描述统计2.2方差齐性检验由莱文等同性检验可得:F=1.659,P=0.196>0.05,不能拒绝原假设,认为三组数据是方差齐性的。
2.3总体均数检验由主体间效应检验结果可得:F=13.482,P=0.000<0.05,因此要拒绝原假设,认为3个处理组患者的低密度脂蛋白含量总体均数不全相等,即不同剂量药物对低密度脂蛋白含量的降低有影响。
2.4多重比较表格给出了不同方法的多重比较结果,我们以LSD的结果为例进行解读。
分组1与分组2之间的P值为0.000,结合两组间的均值大小可以得出:降血脂新药2.4g组低密度脂蛋白含量均数低于安慰组;分组1与分组3之间的P值为0.000,结合两组间的均值大小可以得出:降血脂新药4.8g组低密度脂蛋白含量均数低于安慰组;分组2与分组3之间的P值为0.914,说明2.4g组和4.8g组低密度脂蛋白含量均数相等,不存在差异性,但是分组3的均值更小一些,所以4.8g组降低低密度脂蛋白的效果更强。
如何开展方差分析与多重比较30天学会医学统计与SPSS公益课(D6)t检验主要用于两组定量正态分布的数据比较,但是如果需要比较多组定量数据,t检验分析方法很可能不合适,此时,必须要借助另外一种方法,方差分析,英文缩写ANOVA(ANalysis Of VAriance),又称F检验。
实例分析在评价某临床新药耐受性及安全性的2a期临床试验中,对符合纳入标准的30名健康自愿者随机分为3组,每组10名。
各组注射剂量分别为0.5U、1U、2U,观察48小时部分凝血活酶时间(s),试问不同剂量的部分凝血活酶时间有无不同?数据库见time48.sav1思考这个案例来源于上一讲,需要思考:-这个案例由几个变量组成?-研究的结局变量是什么?-结局变量属于什么类型的变量?-如果是定量变量数据,是偏态还是正态分布?-研究目的是比较,那比较的组数是多少?2案情分析这个案例包括2个变量,一个是活酶时间(s),另外一个是分组变量。
主要研究的结局指标是活酶时间,为定量变量数据;比较的组数是3组(0.5单位/1单位/2单位)。
本案例目的是比较多组总体均数有无统计学差异。
3统计分析策略多组定量数据的比较,基本的方法有2种。
一种是成组F检验,一种是多样本的非参数秩和检验(Kruskal Wallis 秩和检验)。
究竟采用哪种方法,必须考虑“三个性”的条件:正态性、独立性、方差齐性。
关于“三个性”的解释,可以看Day 3:成组t检验的文章,此处不再赘述。
总的来说,方差分析针对两组或以上、定量、正态、独立、方差齐的数据比较。
前面2个要求和多样本的非参数秩和检相同,差别在于F检验要求数据符合正态性、独立性、方差齐性三个要求。
此外,如果细心的朋友可能会注意到,这里方差分析的条件是2组或以上,也就是方差分析不仅处理多样本,也同样可以处理2样本,关于这一点,我最后进行解释。
总结来说,对于本例:本例采用随机化分组设计,独立性符合。
正态性方面,采用的是多样本正态性检验方法,探讨各组是否均来自于正态分布总体。
SPSS单因素和多因素方差分析法SPSS是一种广泛应用于社会科学研究中的数据分析软件。
它提供了一系列功能强大的统计工具,用于分析各种数据。
在SPSS中,单因素和多因素方差分析法是常用的统计方法之一,用于比较两个或多个组之间的差异。
单因素方差分析法又称单变量方差分析,用于比较一个自变量(也称为因子或组别)对于一个因变量(也称为依变量或观察变量)的影响。
它适用于多个组之间存在一个自变量的情况。
例如,假设我们想要比较三种不同讲义对学生阅读理解成绩的影响,我们可以将讲义视为自变量,阅读理解成绩视为因变量。
通过单因素方差分析,我们可以确定这三个组之间是否存在显著差异。
多因素方差分析法又称多变量方差分析,用于比较两个或多个自变量对于一个因变量的影响。
它适用于多个组之间存在多个自变量的情况。
例如,假设我们想要比较四种不同肥料对植物生长的影响,我们可以将肥料的种类和施肥时间视为两个自变量,植物生长情况视为因变量。
通过多因素方差分析,我们可以确定这四个组之间是否存在显著差异,并确定哪个自变量或哪些自变量对于植物生长有较大的影响。
在SPSS中进行单因素和多因素方差分析的步骤大致相似。
首先,我们需要将数据输入到SPSS中。
然后,我们需要选择适当的分析方法。
对于单因素方差分析,我们选择“统计”菜单下的“方差分析”选项。
对于多因素方差分析,我们选择“统计”菜单下的“一般线性模型”选项。
接下来,我们需要选择自变量和因变量,并指定相应的因子水平或组别。
最后,我们需要运行分析并查看结果。
分析结果包括多个方面的信息。
首先,我们可以看到各组之间的均值差异以及是否显著。
通过协方差差异分析表,我们可以判断方差分析的显著水平。
如果方差分析的显著水平小于0.05,则说明至少有一组之间存在显著差异。
此外,还可以查看效应大小,以确定自变量对因变量的影响程度。
最后,通过多重比较(如Tukey's HSD),我们可以确定哪些组之间存在显著差异。
文章编号:100023711(2007)022000120用SPSS实现完全随机设计多组比较秩和检验的多重比较3刘万里,薛 茜,曹明芹,马金凤(新疆医科大学公共卫生学院,乌鲁木齐830054)摘要:目的 针对医学研究中常见的完全随机设计多组样本资料数据经Kruskal-W allis H检验后无法直接用SPSS实现各组多重比较的问题,给予用SPSS统计软件具体解决方案。
方法 根据资料特点和样本量大小,结合SPSS软件本身的一些特点,在SPSS中实现秩和检验的多重比较。
结果 对同一数据资料进行处理,所得结论基本相同。
结论 本文提供了用SPSS软件实现该种数据分析的详细过程,分析人员可结合不同的工作,采用统计软件正确地完成此类数据的分析工作。
关键词:多重比较;秩和检验;SPSS中图分类号:R195.1文献标识码:ANonparam eti c Test of Co m pletely Rando m i zed D esi gn andM ulti ple Co m par ison s w ith SPSSL I U W an-li,XUE Q ian,CAO M ing-qin,MA J in-feng(College of Public Hea lth,X injiang M ed ical U niversity,U ruq m i,X injiang830054,China)Abstract:O bjecti ve I n vie w of the medical research in comp letely random ized design,the multi-gr oup s sa mp le material data can not be tested by multi p le comparis ons p r ocedures directly t o realize each gr oup with SPSS.W e give the methods of multi p le comparis ons with SPSS.M ethods According t o the material characteristic and the sa mp le quantity size,multi p le comparis ons are realized in SPSS by combining s oft w are itself s o me characteristics.Results The data analysis with each methods has the sa me results.Conclusi on s This paper gives references t o related medical research and data analysis with SPSS.Key words:Multi p le comparis on;Nonpara metic test;SPSS 秩和检验是医学科研工作中较为常用的一大类非参数统计方法,该方法对资料分布没有特殊要求,除了用于计量资料外,还可用于对样本数据的符号、等级程度、大小顺序等进行比较,方法简便。
SPSS 多重比较方法(信息摘自网络,仅供参考)(一)常用方法总结1.LSD法 最小显著差异法,公式为:它其实只是t检验的一个简单变形,并未对检验水准做出任何校正,只是在标准误的计算上充分利用了样本信息, 为所有组的均数统一估计出了一个更为稳健的标准误,其中MS误差是方差分析中计算得来的组内均方,它一般用于计划好的多重比较。
由于单次比较的检验水准仍为α,因此可认为LSD法是最灵敏的。
2.Bonferroni法 该法又称Bonferroni t检验,由Bonferroni提出。
用t检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
若每次检验水准为α′,共进行m 次比较,当H0 为真时,犯Ⅰ类错误的累积概率α不超过mα′,既有Bonferroni不等式α≤mα′成立。
3.Sidak法 它实际上就是Sidak校正在LSD法上的应用,即通过Sidak校正降低每两次比较的Ⅰ类错误概率,以达到最终整个比较的Ⅰ类错误概率为α的目的。
即α′= 1 - (1 -α) 2 / k ( k - 1) ,计算t统计量进行多重配对比较。
可以调整显著性水平,比Bofferroni方法的界限要小。
4.Student-Newman-Keuls法( SNK法)它实质上是根据预先制定的准则将各组均数分为多个子集, 利用Studentized Range分布来进行假设检验,并根据所要检验的均数的个数调整总的Ⅰ类错误概率不超过α。
用student range分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小按顺序排列,最先比较最末端的差异。
5.Dunnett检验常用于多个试验组与一个对照组间的比较,根据算得的t值,误差自由度ν误差、试验组数k - 1以及检验水准α查Dunnett-t界值表,作出推断。
6.Duncan法(新复极差法)(SSR)指定一系列的“range”值,逐步进行计算比较得出结论。
7.Tukey检验使用学生化的范围统计量进行组间所有成对比较。
将试验误差率设置为所有成对比较的集合的误差率。
Tukey的应用指征:(1)所有各组的样本数相等;(2)各组样本均数之间的全面比较;(3)可能产生较多的假阴性结论。
8.Scheffe检验为均值的所有可能的成对组合执行并发的联合成对比较。
使用 F 取样分布。
可用来检查组均值的所有可能的线性组合,而非仅限于成对组合。
Scheffe 的应用指征:(1)各组样本数相等或不等均可以,但是以各组样本数不相等使用较多;(2)如果比较的次数明显地大于均数的个数时,Scheffe法的检验功效可能优于Bonferroni法和Sidak法。
如均数的个数等于或小于比较的次数,Bonferroni方法较Scheffe方法佳。
(二)各种方法简介-11. 方差齐时,可选用以下方法:LSD:least significant difference检验法,指用t检验对各组均值间进行配对比较。
对多重比较误差率不进行调整。
Bonferroni:用t检验对各组间均值进行配对比较,通过设置每个检验的误差率来控制整个误差率。
Sigdk:为计算t统计量进行多重配对比较。
可以调整显著性水平,比Bonferroni方法的界限要小。
Scheffe:为对所有可能的配对组合进行同步配对比较。
可以同时检验所有均数的线性组合。
不单纯是配对均值的比较。
R-E-G-W F:为作Ryan-Einot-Gabriel-Welsch F检验法,用F检验进行多重比较检验。
R-E-G-W Q:为作Ryan-Einot-Gabriel-Welsch检验法,用t化极差进行多重配对比较。
S-N-K:为Student-Newman-Keuls检验法,用t化极差分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了用所有各组样本含量的调和平均数进行样本量估计时,用逐步过程进行齐次子集(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小的顺序排列。
最先比较极端的差异。
Tukey:为作Tukey's honestly significant difference检验法,用t化极差统计量进行所有组间均值的配对比较,用所有配对比较误差率作为实验误差率。
Tukey's-b:用t化极差分布进行组间均值的配对比较。
其精确值为前两种检验相应值的平均值。
Duncan:为作Duncan's multiple range检验法指定一系列的t化极差值,逐步进行计算比较得出结论。
Hochberg's GT2:用正态最大系数进行多重比较。
Gabriel:用正态标准系数进行配对比较,在单元数较大时,这种方法较自由。
Waller-Duncan:用t统计量进行多重比较检验。
使用Bayesian逼近。
Dunnett:用于多个处理组与一个对照组配对比较。
选定此方法后,激活下面的Control categories框,选择对照组,有两个选项Lase(默认选项)和First。
Test框内选择检验的单双侧。
选项2-side表示双侧检验(默认选项);选项<control为单侧检验表示处理组均数小于对照组均数;选项>control 为单侧检验表示处理组均数大于对照组均数。
2. 方差不齐时可以选用以下方法:Tamhane's T2:t检验进行配对比较。
Dunnett's T3:t化最大值下的配对比较。
Games-Howell:方差不具齐次性时的配对比较,方法较灵活。
Dunnett's C:t化极差下的配对比较。
注:在LSD以及Duncan法的计算结果的表示方法为把差异没有显著性意义的比较组列在同一列里。
没有列出的其余各比较组之间差异均有显著性意义。
(三)各种方法简介-21. 假定方差齐性•LSD.使用t 检验执行组均值之间的所有成对比较。
对多个比较的误差率不做调整。
LSD法侧重于减少第二类错误,此法精度较差,易把不该判断为显著的差异错判为显著,敏感度最高。
LSD法的使用:在进行试验设计时就确定各处理只是固定的两个两个相比,每个处理平均数在比较中只比较一次。
例如,在一个试验中共有4个处理,设计时已确定只是处理1与处理2、处理3与处理4(或1与3、2与4;或1与4、2与3)比较,而其它的处理间不进行比较。
因为这种比较形式实际上不涉及多个均数的极差问题,所以不会增大犯I型错误的概率。
•Bonferroni. Bonferroni提出,设H0为真,如果进行m次显著性水准为α的假设检验时,犯Ⅰ类错误的累积概率α’不超过mα,即有Bonferroni不等式α’≤mα成立。
所以令各次比较的显著性水准为a=0.05/m,并规定P≤0.05/m时拒绝H0,基于这样的做法,就可以把Ⅰ类错误的累积概率控制在0.05。
这种对检验水准进行修正的方法叫做Bonferroni调整(Bonferroni adjustment)法,简称Bonferroni法。
使用t 检验在组均值之间执行成对比较,但通过将每次检验的错误率设置为实验性质的错误率除以检验总数来控制总体误差率。
这样,根据进行多个比较的实情对观察的显著性水平进行调整。
换句话来说,Bonferroni法由LSD修正而来,通过设置每个检验的α水准来控制总的α水准。
但是比较的次数越多,比较的结果越保守。
Bonferroni法的应用指征:(1)各组的样本数无论相等还是不等;(2)计划好的某两个组间或几个组间作两两比较;(4)当比较次数不多时,Bonferroni法的效果较好;(5)但当比较次数较多(例如在10次以上)时,则由于其检验水准选择得过低,结论偏于保守,犯Ⅱ类错误的概率增加,即出现较多的假阴性结果;(6)Bonferroni法比LSD法、Duncan法、SNK法偏于保守,不过,它比Tukey法、Scheffe法要敏感。
•Sidak.基于t 统计量的成对多重比较检验。
Sidak 调整多重比较的显著性水平,并提供比Bonferroni 更严密的边界。
•Scheffe.(最常用,不需要样本数目相同)为均值的所有可能的成对组合执行并发的联合成对比较。
使用 F 取样分布。
可用来检查组均值的所有可能的线性组合,而非仅限于成对组合。
Scheffe的应用指征:(1)各组样本数相等或不等均可以,但是以各组样本数不相等使用较多;(2)如果比较的次数明显地大于均数的个数时,Scheffe法的检验功效可能优于Bonferroni法和Sidak法。
如均数的个数等于或小于比较的次数,Bonferroni方法较Scheff’e方法佳。
• R-E-G-W F.基于 F 检验的Ryan-Einot-Gabriel-Welsch 多步进过程。
• R-E-G-W Q. 基于学生化范围的Ryan-Einot-Gabriel-Welsch 多步进过程。
•S-N-K.使用学生化的范围分布在均值之间进行所有成对比较。
它还使用步进式过程比较具有相同样本大小的同类子集内的均值对。
均值按从高到低排序,首先检验极端差分。
•Tukey.(最常用,需要样本数目相同)使用学生化的范围统计量进行组间所有成对比较。
将试验误差率设置为所有成对比较的集合的误差率。
Tukey 的应用指征:(1)所有各组的样本数相等;(2)各组样本均数之间的全面比较;(3)可能产生较多的假阴性结论。
•Tukey's b.使用学生化的范围分布在组之间进行成对比较。
临界值是Tukey's 真实显著性差异检验的对应值与Student-Newman-Keuls 的平均数。
• Duncan. 使用与Student-Newman-Keuls 检验所使用的完全一样的逐步顺序成对比较,但要为检验的集合的错误率设置保护水平,而不是为单个检验的错误率设置保护水平。
使用学生化的范围统计量。
•Hochberg's GT2. 使用学生化最大模数的多重比较和范围检验。
与Tukey's 真实显著性差异检验相似。
• Gabriel. 使用学生化最大模数的成对比较检验,并且当单元格大小不相等时,它通常比Hochberg's GT2 更为强大。
当单元大小变化过大时,Gabriel 检验可能会变得随意。
• Waller-Duncan. 基于t 统计的多比较检验;使用Bayesian 方法。
• Dunnett.将一组处理与单个控制均值进行比较的成对多重比较t 检验。
最后一类是缺省的控制类别。
另外,您还可以选择第一个类别。
双面检验任何水平(除了控制类别外)的因子的均值是否不等于控制类别的均值。
<控制检验任何水平的因子的均值是否小于控制类别的均值。