迭代法求解线性方程组的研究(精选.)

第二章解线性代数方程组的迭代法2. 1 引言在许多实际问题中，常常需要求解这样的线性代数方程组，它的系数矩阵数很高，但非零元素很少，人们称其为大型稀疏线性代数方程组，对于这类方程组，如果它乂不具有带状性，那么，再用直接法求解就不太有效，因为用直接法进行消元或矩阵的三角分解时，没有考虑到系数矩阵的稀疏性，破坏了系数矩阵的形状，导致了计算量的增加和存储单元的浪费，于是，人们常用迭代法求解大型稀疏线性代数方程组。

迭代法只需要存储系数矩阵的非零元素，这样，占用内存在单元较少，能解高阶线性代数方程组。

山于迭代法是通过逐次迭代来逼近方程组的解，因此，收敛性和收敛速度是构造迭代法时要注意的问题。

那么，是否可以构造一种适用于一般情况的迭代法呢？回答是否定的，这是因为不同的系数矩阵具有不同的性态，一般地，每一种迭代法都具有一定的适用范围，在本章的学习中将会看到，有时，某种方法对一类方程组迭代收敛，而对另一类方程组进行迭代时就会发散。

因此，我们应该学会针对具有不同性质的线性代数方程组，构造合适的迭代方法。

本章主要介绍一些基本的迭代法，并在一定的范围内讨论其中儿种方法的收敛法。

2. 2 基本迭代法考虑线性方程组如坷+如勺+…+气兀”二勺a2t x i+a22x2 + - + a2…x n =b2■•••••••••••(2. 1)采用矩阵和向量记号，我们可以把(2.1)式写成Ax = h(2.2)其中，为非奇异矩阵，设下面我们介绍雅可比(Jacobi)迭代，高斯-塞德尔(Gauss-Seidel)迭代与S0R迭代以及SS0R迭代的基本思想和算法。

为了方便地给出矩阵表示式，我们引进下列矩阵分裂：4SD-U,(2.3)其中-a2\-a n\(1)雅可比迭代的基本思想从式(2.1)的第i个方程中解出X t=(/ = 1,2,•••,«)我们把迭代前面的值代入上式右边，山计算得到等式左边的值作为一次迭代的新值，然后再把这个新值代入右边，再从左边得到一个新值，如此反复，就得到了雅可比迭代公式。

牛顿迭代法求解方程组一、牛顿迭代法的基本原理牛顿迭代法是一种用于求解方程的迭代方法，其基本思想是通过不断逼近方程的根来求解方程。

具体而言，对于一个方程f(x) = 0，我们可以选择一个初始近似解x0，然后通过迭代的方式不断更新x 的值，直到满足一定的停止准则为止。

牛顿迭代法的更新公式如下：x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}其中，x_n表示第n次迭代得到的近似解，f(x_n)表示方程在x_n处的函数值，f'(x_n)表示方程在x_n处的导数值。

二、牛顿迭代法在求解方程组中的应用牛顿迭代法不仅可以用于求解单个方程，还可以推广到求解方程组的情况。

假设我们要求解一个由m个方程和n个未知数组成的方程组，即F(x) = 0其中，F(x) = (f1(x1, x2, ..., xn), f2(x1, x2, ..., xn), ..., fm(x1, x2, ..., xn))为方程组的向量函数。

我们可以将该方程组转化为一个等价的非线性方程组：f(x) = 0其中，f(x) = (f1(x1, x2, ..., xn), f2(x1, x2, ..., xn), ..., fm(x1, x2, ..., xn))。

牛顿迭代法在求解方程组时的更新公式如下：x_{n+1} = x_n - J^{-1}(x_n) f(x_n)其中，J(x_n)是方程组在x_n处的雅可比矩阵，其定义为：J(x_n) = \begin{pmatrix} \frac{\partial f_1}{\partial x_1}(x_n) & \frac{\partial f_1}{\partial x_2}(x_n) & \cdots & \frac{\partial f_1}{\partial x_n}(x_n) \\ \frac{\partial f_2}{\partial x_1}(x_n) & \frac{\partial f_2}{\partial x_2}(x_n) & \cdots & \frac{\partial f_2}{\partial x_n}(x_n) \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1}(x_n) & \frac{\partial f_m}{\partial x_2}(x_n) & \cdots & \frac{\partial f_m}{\partial x_n}(x_n) \end{pmatrix}三、牛顿迭代法的收敛性和收敛速度牛顿迭代法在求解方程组时具有较好的收敛性和收敛速度。

数值分析第三章线性方程组迭代法线性方程组是数值分析中的重要问题之一，涉及求解线性方程组的迭代法也是该领域的研究重点之一、本文将对线性方程组迭代法进行深入探讨。

线性方程组的一般形式为AX=b，其中A是一个n×n的系数矩阵，x和b是n维向量。

许多实际问题，如电路分析、结构力学、物理模拟等，都可以归结为求解线性方程组的问题。

然而，当n很大时，直接求解线性方程组的方法计算量很大，效率低下。

因此，我们需要寻找一种更高效的方法来求解线性方程组。

线性方程组迭代法是一种基于迭代思想的求解线性方程组的方法。

其基本思想是通过构造一个序列{xn}，使得序列中的每一项都逼近解向量x。

通过不断迭代，可以最终得到解向量x的一个近似解。

常用的线性方程组迭代法有雅可比迭代法、高斯-赛德尔迭代法和逐次超松弛迭代法等。

雅可比迭代法是其中的一种较为简单的迭代法。

其基本思想是通过分解系数矩阵A，将线性方程组AX=b转化为x=Tx+c的形式，其中T是一个与A有关的矩阵，c是一个常向量。

然后，通过不断迭代，生成序列xn，并使序列中的每一项都逼近解向量x。

高斯-赛德尔迭代法是雅可比迭代法的改进方法。

其核心思想是利用当前迭代步骤中已经求得的近似解向量的信息。

具体而言，每次迭代时，将前一次迭代得到的近似解向量中已经计算过的分量纳入计算，以加速收敛速度。

相比于雅可比迭代法，高斯-赛德尔迭代法的收敛速度更快。

逐次超松弛迭代法是高斯-赛德尔迭代法的改进方法。

其核心思想在于通过引入一个松弛因子ω，将高斯-赛德尔迭代法中的每次迭代变为x[k+1]=x[k]+ω(d[k+1]-x[k])的形式，其中d[k+1]是每次迭代计算得到的近似解向量的一个更新。

逐次超松弛迭代法可以根据问题的特点调整松弛因子的值，以获得更好的收敛性。

除了以上提到的三种迭代法，还有一些其他的线性方程组迭代法，如SOR迭代法、共轭梯度法等。

这些方法都具有不同的特点和适用范围，可以根据问题的具体情况选择合适的迭代法。

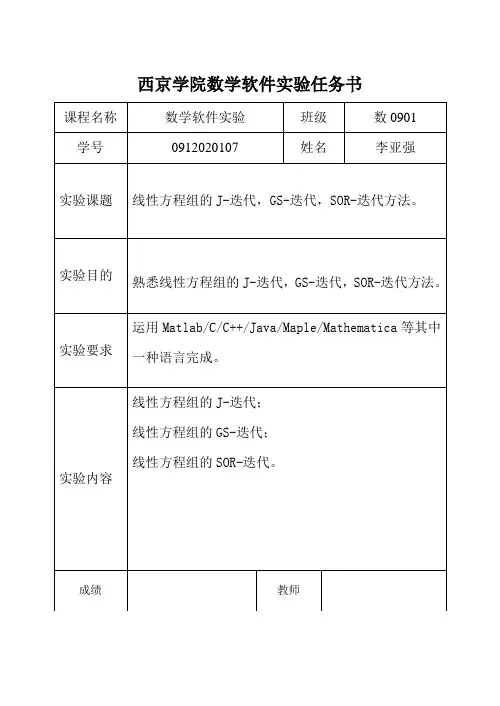
西京学院数学软件实验任务书实验四实验报告一、实验名称：线性方程组的J-迭代，GS-迭代，SOR-迭代。

二、实验目的：熟悉线性方程组的J-迭代，GS-迭代，SOR-迭代，SSOR-迭代方法，编程实现雅可比方法和高斯-赛德尔方法求解非线性方程组12123123521064182514x x x x x x x x +=⎧⎪++=⎨⎪++=-⎩的根，提高matlab 编程能力。

三、实验要求：已知线性方程矩阵，利用迭代思想编程求解线性方程组的解。

四、实验原理：1、雅可比迭代法（J-迭代法）：线性方程组b X A =*，可以转变为：迭代公式(0)(1)()k 0,1,2,....k k J XXB X f +⎧⎪⎨=+=⎪⎩ 其中b M f U L M A M I B J 111),(---=+=-=，称J B 为求解b X A =*的雅可比迭代法的迭代矩阵。

以下给出雅可比迭代的分量计算公式，令),....,()()(2)(1)(k n k k k X X X X =，由雅可比迭代公式有b XU L MXk k ++=+)()1()(，既有i ni j k i iji j k iij k iij b X aXa X a +--=∑∑+=-=+1)(11)()1(，于是，解b X A =*的雅可比迭代法的计算公式为⎪⎩⎪⎨⎧--==∑∑-=+=+)(1),....,(111)()()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 2、 高斯-赛德尔迭代法（GS-迭代法）：GS-迭代法可以看作是雅可比迭代法的一种改进，给出了迭代公式：⎪⎩⎪⎨⎧--==∑∑-=+=+++)(1),....,(111)1()1()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 其余部分与雅克比迭代类似。

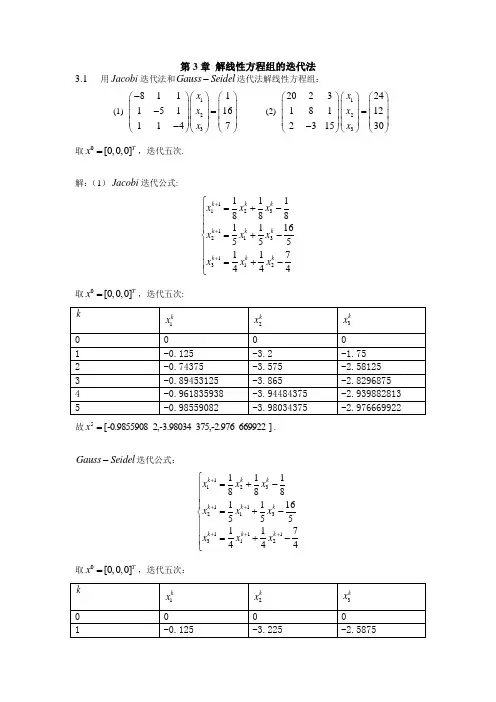
第3章 解线性方程组的迭代法3.1 用Jacobi 迭代法和Gauss Seidel -迭代法解线性方程组：(1)1238111151161147x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭(2)12320232418112231530x x x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭取0[0,0,0]Tx =，迭代五次.解：（1）Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=+++4741415165151818181211331123211k k k k k k k k k x x x x x x x x x取0[0,0,0]Tx =，迭代五次:kk x 1k x 2 kx 30 01 -0.125 -3.2 -1.75 2 -0.74375 -3.575 -2.581253 -0.89453125 -3.865-2.8296875 4 -0.961835938 -3.94484375 -2.939882813 5 -0.98559082-3.98034375 -2.976669922故]669922375,-2.9762,-3.98034-0.9855908[5=x .Gauss Seidel -迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=++++++4741415165151818181121113311123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =，迭代五次：kk x 1 k x 2 kx 31 -0.125-3.225 -2.58752 -0.8515625 -3.8878125 -2.934843753 -0.977832031 -3.982535156 -2.9900917974 -0.996578369 -3.997334033 -2.998478101 5-0.999476517 -3.999590923 -2.99976686故]997668690923,-2.917,-3.9995-0.9994765[5=x（2）Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧++-=+--=+--=+++25115223818156203101211331123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =，迭代五次:kk x 1 k x 2 kx 30 0 1 1.2 1.5 2 2 0.75 1.12.14 3 0.769 1.13875 2.124 0.768125 1.138875 2.125216667 5 0.767331.1383322922.125358333故]32.12535833138332292,0.76733,1.[5=x .Gauss Seidel -迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧++-=+--=+--=++++++25115223818156203101121113311123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =，迭代五次：kk x 1 k x 2 kx 30 0 1 1.2 1.352.112 0.74851.14268752.12873753 0.766420625 1.138105234 2.12543163 4 0.767374732 1.138399205 2.12536321 50.767355598 1.138410149 2.12536795故]6795149,2.12538,1.1384100.76735559[5=x3.2 用Jacobi 迭代法解线性方程组123101091102702108x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭， 取初值向量0[0,0,0]Tx =，要求13||||10k k x x --∞-≤，并讨论方差的收敛性.解：Jacobi 迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=++=+=+++1081021071021011091012133112211k k k k k k k x x x x x x x取初值向量0[0,0,0]Tx =kk x 1 k x 2 kx 30 0 0 1 0.9 0.7 0.8 2 0.97 0.95 0.94 3 0.995 0.985 0.99 4 0.9985 0.9975 0.997 5 0.99975 0.99925 0.9995 6 0.9999250.999875 0.9998535610000625.0||-≤=-x x ，迭代6次后可以得到满足误差要求的解； ]99985.999875,0.0.999925,0[6=x ，Jacobi 迭代法收敛.3.3 社线性方程12311112211x x ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭讨论解该线性方程的Jacobi 迭代法和Gauss Seidel -迭代法的收敛性. 解：按Jacobi 迭代法展开：⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎭⎫ ⎝⎛-=010220022010111122111221U L D A(1) 对于Jacobi 迭代法，其迭代矩阵为：⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-----⎪⎪⎪⎭⎫⎝⎛=+=--022101220022101220111)(11L U D B J J B 的特征矩阵为：3221122||λλλλλ=⎪⎪⎪⎭⎫⎝⎛-=-J B I 解得03,2,1=λ10)(<=J B ρ，故Jacobi 迭代法收敛.(2) 对Gauss Seidel -迭代法，其迭代矩阵为：⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛------=-=--200320220010220122111)(11U L D B G G B 的特征矩阵为：2)2(20032022||-=⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλG B I 解得：01=λ，23,2=λ12)(>=G B ρ，故Gauss Seidel -迭代法发散.3.4 设线性方程组1122332313a x b a x b ⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中a 为参数，且0a ≠，试求a 的取值范围，使得解该线性方程组的Jacobi 迭代法收敛.解：按Jacobi 迭代法展开：⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎭⎫ ⎝⎛---=030120031020313212a a a U L D a a a AJacobi 迭代法，其迭代矩阵为：⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-031302120313********)(1aaa a a a a aaU L D B J J B 的特征矩阵为：)14(313212||2a aaa a a aB I J +=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλ 解得01=λ，i a 142=λ，当1|14||14|)(<==ai a B J ρ，即14||>a 时，Jacobi 迭代法收敛.3.5 用Gauss Seidel -迭代法解线性方程组123142*********x x x --⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 是否收敛？若不收敛，则能否改写成线性方程组，使得Gauss Seidel -迭代法收敛.解：（1）按Gauss Seidel -迭代法展开：⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=--=⎪⎪⎪⎭⎫ ⎝⎛--=000240020040411420014241U L D A 对Gauss Seidel -迭代法，其迭代矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-=-=--480816024000024025.05.02014000000240420141)(11U L D B G G B 的特征矩阵为：)20(480816024||2-=⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλG B I 120)(>=G B ρ,Gauss Seidel -迭代法发散.（2）将A 改写成严格对角占优矩阵，则Gauss Seidel -迭代法必收敛，比如：⎪⎪⎪⎭⎫ ⎝⎛=120014241C对Gauss Seidel -迭代法，其迭代矩阵为：⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛=-=--163208160240000240128014001000240120141)(11U L D B G G B 的特征矩阵为：316320816024||λλλλλ=⎪⎪⎪⎭⎫⎝⎛+--=-G B I 10)(<=G B ρ,Gauss Seidel -迭代法收敛.3.7 设迭代法f Bx x k k +=+1，,...)2,1,0(=k ，的迭代矩阵B 的谱半径()0B ρ=，试证明该迭代法最多迭代n 次便可得到方程组x Bx f =+的解*x ，即*n x x =.解：n 阶矩阵B 一定相似于它的若当标准型J ，即存在可逆矩阵P 使得1P BP J -=，因为()0B ρ=，故B 的特征值全为0，于是得：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=000 J 由此可知0n J =.x Bx f =+显然有唯一解*x ，即**x Bx f =+，又1**()k k x x B x x +-=-，于是()*2(2)*(0)*()()n n n x x B x x B x x --=-==-又因为1110n n P BP J B P JP B P J P ---=⇒=⇒==所以()*0n xx -=，即*n x x =.3.8 给定线性方程组Ax b =，其中323,121A b ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦若用迭代法,...)1,0)((1=-+=+k b Ax x x k k k α，求解，问：（1） 实数取何值时该迭代法收敛；（2） 实数取何值时该迭代法收敛最快. 解：该迭代公式可改写为b x A I x k k αα-+=+)(1，其对应的迭代矩阵为：⎪⎪⎭⎫⎝⎛+++=+=ααααα21231A I B ， B 的特征矩阵为：)]1()][41([)21()2()31(||αλαλαλαααλλ+-+-=⎪⎪⎭⎫ ⎝⎛+--+-+-=-B I ， 解得αλ411+=，αλ+=12，41,0.4()max{|14|,|1|}1,0.4014,0,B ααραααααα--<-⎧⎪=++=+-<<⎨⎪+>⎩（1）1)(<B ρ，即⎩⎨⎧<+<+1|1|1|41|αα，解得021<<-α，该迭代法收敛.（2）在021<<-α上，当4.0-=α时，)(B ρ达到最小，该迭代法收敛最快.3.9 用SOR 迭代法解线性方程1233.21141 3.71 4.511 4.25x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 取初始向量0[0,0,0]Tx =， 1.25ω=，迭代三次，并讨论其收敛性. 解：SOR 迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧--+-=--+-=--+-=++++++)5(2.4)1()5.4(7.3)1()4(2.3)1()1(2)1(1)(3)1(3)(3)1(1)(2)1(2)(3)(2)(1)1(1k k k k k k k k k k k k x x x x x x x x x x x x ϖϖϖϖϖϖ 取初始向量0[0,0,0]Tx =， 1.25ω=，迭代三次，kk x 1k x 2 kx 31 1.56250.992398649 0.727708736 2 0.499958053 0.857418315 0.902186992 3 0.7501646640.747688781 0.816758774]58774781,0.81674,0.7476880.75016466[)3(=x因A 为对称正定矩阵，10)(<=A ρ，SOR 迭代法必收敛.3.11 用SOR 迭代法解线性方程组123410114140143x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭其精确解*11[,1,]22Tx =-，分别取 1.03ω=，1ω=， 1.1ω=，要求当*5||||10kx x -∞-≤时迭代终止，并且对每一个ω值确定迭代次数. 解：用SOR 迭代公式：(1)()()112(1)()(1)()2213(1)()(1)332(1)[1]4(1)[4]4(1)[3]4k k k k k k k k k k x x x x x x x x x x ϖωϖωϖω+++++⎧=-++⎪⎪⎪=-+++⎨⎪⎪=-+-+⎪⎩(1) 取初值向量0[0,0,0]Tx =，当 1.03ω=时k错误!1kx2k x 3k x0 01 0.25751.09630625 -0.490201141 2 0.532073859 1.007893038 -0.498261509 3 0.501070241 1.000486458 -0.499926892 4 0.500093156 1.000028219 -0.499994927 5 0.500004472 1.000001611 -0.499999737 60.500000281 1.000000092 -0.4999999846*5||||0.00000028110x x -∞-=≤，迭代6次后得到满足精度要求的根：]999984092,-0.4991,1.0000000.50000028[6=x(2) 取初值向量0[0,0,0]Tx =，当1ω=时k错误!1kx2k x 3k x0 0 01 0.251.0625 -0.484375 2 0.515625 1.0078125 -0.498046875 3 0.501953125 1.000976563 -0.499755859 4 0.500244141 1.00012207 -0.499969482 5 0.500030518 1.000015259 -0.499996185 6 0.500003815 1.000001907 -0.499999523 70.500000477 1.000000238 -0.499999947*5||||0.00000047710x x -∞-=≤，迭代7次后得到满足精度要求的根：]99994238,-0.4997,1.0000000.50000047[7=x(3) 取初值向量0[0,0,0]Tx =，当 1.1ω=时k错误!1kx2k x 3k x0 010.275 1.175625 -0.5017031252 0.570796875 1.001438281 -0.499434163 0.49331584 0.998173634 -0.500558835 4 0.500166165 1.000074653 -0.499923587 5 0.500003913 1.000014624 -0.500003626 0.50000363 0.999998541 -0.5000000397 0.499999236 0.999999925 -0.5000000177*5||||0.00000076436110x x -∞-=≤，迭代7次后满足精度要求.3.12 考虑迭代法,...)1,0(1=+=+k f Bx x k k其中⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=021212102121210B ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=21121f 证明：该迭代法收敛，取初始向量0[0,0,0]Tx =，计算4x . 证：B 的特征矩阵为3212121212121||λλλλλ=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=-B I 0)(=B ρ，该迭代法收敛.该迭代法的迭代公式为：⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=++=--=+++21212112121212121211331123211k k k kk k k k k x x x x x x x x x 取初始向量0[0,0,0]Tx =，迭代四次：k错误!1kx2k x 3k x0 0 0 0 1 -0.5 1 -0.5 2 0.353553391 0.5 -0.353553391 3 0 1 0 40 1 0 故]0,1,0[)4( x。

收稿日期：2021-02-01基金项目：晋中信息学院“线性代数”教学团队建设项目；晋中信息学院“概率论与数理统计”精品课程项目.作者简介：白雪婷，女，山西吕梁人，晋中信息学院讲师；杨琴乐，晋中信息学院（山西晋中030800）.2021年第4期第42卷总第313期学报解线性方程组的VRP-GMRES （m ）迭代法白雪婷，杨琴乐摘要：为更有效求解科学研究与工程计算中大规模线性方程组问题，该文提出一种变参数重启动GMRES （m ）算法，即VRP-GMRES （m ）算法，通过适当地变化GMRES （m ）算法中的重启动参数m ，很好地解决了GMRES （m ）算法在执行时因参数m 选择不当造成的迭代停滞问题.另外，利用Givens正交变换证明新算法不仅收敛，而且计算精度更高.数值算例表明，VRP-GMRES （m ）算法可显著提高GMRES （m ）算法的计算效率和计算精度，其优越性随着计算问题规模的增大而更加明显，具有广阔的工程应用前景.关键词：VRP-GMRES （m ）算法；Givens 变换；变参数；收敛性；计算精度中图分类号：O29文献标志码：A文章编号：1008-7974（2021）04-0022-08DOI ：10.13877/22-1284.2021.04.004应用科学、物理和工程领域许多问题可建立偏微分方程的数学模型，这些微分方程经过离散后一般都可归结为求解大型稀疏线性方程组Au =b ，A ∈R n ×n，u ，b ∈R n ，其中A 为非奇异矩阵.这类方程组的求解通常采用迭代法.目前，以Galerkin 原理为基础建立的广义极小残余GMRES （m ）迭代法是求解此类方程组最有效的方法之一.因此，近年来GMRES （m ）算法及其在其他领域的应用一直是人们研究的热点［1-4］.实际计算表明，当系数矩阵A 是良态矩阵时，GMRES （m ）算法及一些简单改进后的GMRES （m ）算法便可有效地求解这些线性系统［5-6］，但如果系数矩阵A 具有很强的病态性，则必须结合一些特定的预处理技术［7-10］.不管是GMRES （m ）算法还是预处理GMRES （m ）算法，在实际执行这些算法时，参数m 一旦选定，在之后整个迭代过程当中将始终固定不变.所以参数m 的选择也是影响算法有效执行的关键因素之一.研究表明，m 取值较小时，有可能出现收敛慢甚至不收敛等现象，m 选择过大会造成存储空间过多的需求.因此，如何选择一个合适的参数m 一直困扰着众多学者，最近有不少学者试图通过变化GMRES（m）算法中的重启动参数m来克服这些困难.BAKE A H最初通过选择随机的参数m来改善GMRES（m）算法的收敛性，后来又根据两次迭代所得残余向量的范数之比来确定参数m的大小，但这也并不能保证算法的收敛性［11-12］，PEAIRS L等则通过强化学习方法来决定参数m的取值，该方法进一步表明适当的参数m可以提高GMRES（m）算法的计算效率，但由于强化学习只是一种机器学习方法，因此存在一定局限性［13］.1GMRES（m）算法基本理论1.1Galerkin原理任意给定向量u0∈R n，令u=u0+z，则方程组Au=b等价于Az=r0，（1）其中：r0=b-Au0是初始残余向量.给定一个参数m>0，设R n中两个m维子空间K m和Lm分别为：Km=span {} r0,Ar0,⋯,A m-1r0，Lm=A K m=span {} Ar0,A2r0,⋯,A m r0，且v1,v2,⋯,v m和w1,w2,⋯,w m分别为子空间Km和L m的基.令V m={}v i m i=1，W m={}w i m i=1.求解式（1）的Galerkin原理为：给定一个m>0，寻找近似解z m=V m y m∈K m，使(r0-Az m)⊥L m，即()r0-AV m y m⊥L m，该式也可表示为()r0-AV m y m,ωi=0,y m∈R m.1.2Arnoldi过程及其性质Arnoldi过程具体如下（文中若不作特殊说明， ⋅均表示向量的二范数）：①对m>0和初始向量v0∈R n.计算v1= r0 r0，其中r0=b-Au0；②对于k=1,2,⋯,m，计算h i,k=()Av k,v i，-vk+1=Av k-∑i=1k h i,k v i，h k+1,k= -v k+1，要求-vk+1⊥v i()i=1,2,⋯,k；③如果h k+1,k=0，停止；否则v k+1= -vk+1h k+1,k.Arnoldi过程有如下重要性质.定理1［14］在Arnoldi过程中，令V m+1= (V m|v m+1)，-H m=éëêùûúH mh m+1,m e T m，则如下关系成立.AV m=V m H m+h m+1,m v m+1e T m，AV m=V m+1-H m,V T m+1V m+1=I，（2）其中：H m=(h ij)m是上海森伯格矩阵，e T m= (0,0,⋯,1)∈R m且I是一个m+1阶单位矩阵.1.3GMRES算法定理2［15］令A为n×n方阵并假定L=AK，u=u0+z=u0+V m y，则由Galerkin原理得到的近似解Z m将使残余向量r0-Az在Krylov 子空间K m中达到最小，反之亦然，并且有r=b-Au=r0-Az=βe1--H m y，（3）其中：β= r0，e1=()1,0,⋯,0T∈R m+1.这个定理表明，在K m中极小化残余向量r0-Az2等价于在R m中极小化βe1--H m y. GMRES（m）算法基本思想就是固定重启动参数m，通过求解最小二乘问题miny∈R mβe1--H m y，迭代计算求得z m，使得 r m=r0-Az m<τ，GMRES（m）算法详细步骤如下：①给定误差上界τ>0，给定一个合适的m()m<n，取u0∈R n，计算r0=b-Au0以及β= r0；②完成Arnoldi过程得{}v i m i=1和-H m；③求解最小二乘问题min y∈R mβe1--H m y，得y m，这里e1=()1,0,⋯,0T∈R m+1；白雪婷，等：解线性方程组的VRP-GMRES（m）迭代法2021年第4期学报④计算z m =V m y m .若 r m= r-Az m<τ，迭代终止；否则，令u m =u 0+z m ，u 0=u m ，转向步骤②.在GMRES （m ）算法中，并非任意选取m 都能使其收敛.事实上，适当地变化m 可以有效地改善GMRES （m ）的收敛性，且在一定程度上可以避免收敛慢甚至不收敛等现象.2VRP-GMRES （m ）算法2.1VRP-GMRES （m ）算法适当变化重启动参数m ，通过迭代使得残余向量 r m=r-Az m<τ，具体过程为：Step1：选择一个较小的初始正整数m ()m ≪n ，给定误差上界τ>0；Step2：执行Arnoldi 过程，得到{}v i m i =1和-H m ；Step3：求解如下最小二乘问题min y ∈R mβe 1--H m y ，（4）可得y m ，计算近似解z m =V m y m ，且令u m =u 0+z m ；Step4：如果 r m=r-Az m<τ，迭代停止，输出u =u m .否则，转向Step5；Step5：令u 0=u m ，m =m +1()m ≤n 转至Step2.实际执行VRP-GMRES （m ）算法时，可能出现收敛慢甚至不收敛等现象（虽然这种情况较少发生）.所以，为防止参数m 过大而造成存储空间过多的需求，可以先执行若干次VRP-GMRES （m ）算法，待m 增加到一定程度且残量范数减小到某一适当值时，再固定m循环迭代，即执行GMRES （m ）算法.2.2收敛分析定义1［15］设G i =éëêêêêêêêêêêêêêêêêùûúúúúúúúúúúúúúúúú1⋱1c i s i -s ic i1⋱1i 行i +1行，（5）其中：实数c 和s 满足c 2i +s 2i =1，称G i 为平面旋转矩阵，也称为Givens （吉文斯）变换矩阵.定理3在VRP-GMRES （m ）算法中，令E = r m ，-E =r m +1，则-E <E .证明在VRP-GMRES （m ）算法中，令式（5）中G i ∈R ()m +1×()m +1，s i =h ()i -1i +1,i()h ()i -1ii2+()h ()i -1i +1,i 2，c i =h ()i -1ii ()h (i -1)ii 2+()h ()i -1i +1,i 2，其中：i =1,2,⋯,m ，h ()i -1i i 和h ()i -1i +1,i 是-H m 经i -1次Givens 正交变换后对角线及次对角线元素.令Q m =G m G m -1⋯G 1，对式（4）中-H m 和βe 1作正交变换，则可得Q m -H m =éëêùûúR m O =-R m ，其中：R m 是m 阶可逆上三角方阵.又Q m ()βe 1=()g Tm ,αT =-g m ，e 1=(1,0,⋯,)0T ∈R m +1，于是min y ∈R mβe 1--H m y=min y ∈R mQ m ()βe 1--H m y =min y ∈R m-g m --R m y =min y ∈Rméëêùûúg m α-éëêùûúR m 0y .解R m y =g m ，得y m .此时E = r m= r-Az m= r-AV m y m=||α.当参数m 变为m +1时，由Arnoldi 过程，有-H m +1=éëêêêêêêùûúúúúúúh 1,m +1-H m⋮h m +1,m +1Oh m +2,m +1.令式（5）中G i ∈R()m +2×()m +2，且s i =h ()i -1i +1,i()h ()i -1ii2+()h ()i -1i +1,i 2，c i =h ()i -1ii ()h (i -1)ii 2+()h ()i -1i +1,i 2，其中：i =1,2,⋯,m +1，取Q m +1=G m +1G m ⋯G 1，对式（4）中-H m 和βe 1作正交变换，则Q m +1-H m +1=éëêùûúR m +1O =-R m +1，其中：R m +1是m +1阶可逆上三角方阵，Q m +1()βe 1=()g Tm +1,-αT =-g m +1，其中：e 1=()1,0,⋯,0T∈R m +2,g m +1∈R m +1.于是miny ∈R m +1βe 1--H m +1y =miny ∈Rm +1Q m +1()βe1--H m +1y =min y∈Rm +1-g m +1--R m +1y =min y ∈Rm +1éëêùûúg m +1-α-éëêùûúR m +10y ，解R m +1y =g m +1，得y m +1.此时Eˉ= r m +1=r 0-Az m +1= r-AV m +1y m +1=||αˉ=||s m +1α<||α=E .（6）由定理3知，VRP-GMRES （m ）算法不仅收敛，而且比GMRES （m ）算法计算精度更高.3数值实验本节通过两个不同类型的数值算例说明VRP-GMRES （m ）算法的有效性和可行性，分析比较GMRES （m ）和VRP-GMRES （m ）两种算法的数值结果.在以下算例中均选取u 0=()0,0,⋯,0T∈R ()n -1作为初始向量， r m =r-Az m <τ=1e -8作为停止迭代标准.算例1考虑如下一维波动方程ìíîïïïïïïïïu tt =4u xx ,0<x <1,0<t <0.5;u ()0,t =u ()1,t =0,0≤t ≤0.5;u ()x ,0=f ()x =sin ()πx +sin ()2πx ,0≤x ≤1;u t()x ,0=g ()x =0,0≤x ≤1.（7）该方程精确解为：u ()x ,t =sin ()πx cos ()2πt +sin ()2πx cos ()4πt ，其中：u ()x ,t 表示振弦，是对特定位置x 和特定时间t 的波强度的一个测量，如图1（a ）所示.用中心差分格式离散后可得Au =b ,A ∈R ()n -1×()n -1,u ,b ∈R n -1，（8）其中：n 表示x 方向和t 方向网格数.用VRP-GMRES （m ）算法求解式（8），计算结果如图1（b ）所示.由图1知，式（7）的数值解和精确解是一致的，这也说明VRP-GMRES （m ）算法的正确性.（a）精确解（b）数值解图1振幅分布（n =10，m =7）白雪婷，等：解线性方程组的VRP-GMRES （m ）迭代法2021年第4期学报分别用GMRES （m ）算法和VRP-GMRES （m ）算法求解式（8），当n =10，m =7时，cond ()A =56.5079.GMRES （m ）算法循环迭代9次后出现迭代停滞，此时残量范数为1.4099，但对于VRP-GMRES （m ）算法，迭代3次后残量范数已达到1.4230e-014.迭代过程各节点绝对误差大小的比较如图2所示.GMRES （m ）算法VRP-GMRES （m ）算法（a）迭代2次后绝对误差GMRES （m ）算法VRP-GMRES （m ）算法（b）迭代3次后绝对误差图2迭代过程中各节点绝对误差大小的比较由图2可知，当迭代次数相同时，用VRP-GMRES （m ）算法比用GMRES （m ）算法得到的计算结果的绝对误差要小得多，而且随着迭代次数的增加，用VRP-GMRES （m ）算法计算产生的绝对误差减少得更快.这说明本文算法不仅具有更高的计算精度，而且能快速收敛.当参数m 分别取不同值时，对两种算法的计算结果进行比较如表1~表4所示.表1~表4分别给出两种算法的迭代次数、运行时间、计算精度和收敛速度比较.从表1~表4可知，文中提出的算法收敛快，稳定性好，计算精度高，运行时间短.参数m 的选择对GMRES （m ）算法至关重要，参数m 选择不当会导致算法失败，而参数m 的选择对VRP-GMRES （m ）算法的执行基本无任何影响.这表明，GMRES （m ）算法对参数m 的选择相当敏感，m 的微小变化可能会导致GMRES （m ）算法出现迭代停滞等现象，而本文提出的VRP-GMRES （m ）算法中参数m 是变化的，在一定程度上降低了GMRES （m ）算法对参数m 的敏感度，这也是VRP-GMRES （m ）算法的优点之一.表1两种算法迭代次数比较n （网格数）102030405060m （重启动参数）81929395485两种算法迭代次数GMRES （m ）算法11331579164VRP-GMRES （m ）算法223121414表2两种算法运行时间比较n （网格数）102030405060m （重启动参数）81929395485两种算法运行时间/s GMRES （m ）算法0.0294150.0289820.0921441.38182523.539635157.340531VRP-GMRES （m ）算法0.0182540.0134420.0861720.8471084.68302614.662790表3两种算法计算精度比较n （网格数）102030405060m （重启动参数）81929395485两种算法计算精度GMRES （m ）算法2.1069e-0091.1751e-0152.0093e-0122.4647e-0093.3092e-0112.0593e-009VRP-GMRES （m ）算法2.9235e-0141.1984e-0155.4751e-0142.1327e-0102.1327e-0106.5913e-013表4两种算法收敛性比较n（网格数）102030405060m （重启动参数）81929395485两种算法收敛性GMRES （m ）算法停滞停滞停滞停滞停滞停滞VRP-GMRES （m ）算法收敛收敛收敛收敛收敛收敛事实上，当网格数n 增大时，系数矩阵A 的条件数也不断增大，当n =59时，A 的条件数已达到2.1098e+003，方程组（8）呈现严重的病态性.由表1知，此时即使参数m 取值很大，GMRES （m ）算法的收敛速度也不是很快，而且在达到给定误差时，GMRES （m ）算法的迭代次数是VRP-GMRES （m ）算法的11.7倍，运行时间是其10.7倍.这表明，随着计算规模地增大，VRP-GMRES （m ）算法比GMRES （m ）算法更有效，有更广阔的前景.算例2考虑如下二维泊松方程{u xx +u yy =2()3x +x 2+y 2,()x ,y ∈Ω=[]0,1×[]0,1;u ()x ,y =x 2()x +y 2+2,()x ,y ∈∂Ω.（9）该方程精确解为u ()x ,y =x 2()x +y 2+2，其中：u ()x ,y 是温度分布函数，温度分布如图3（a ）所示.将式（9）所示的求解区域分别沿x 方向和y 方向n 等分，可得Au =b ,A ∈R ()n -1×()n -1,u ,b ∈R n -1.（10）取n =40，m =10，用VRP-GMRES （m ）求解式（10）时，各节点处的温度分布如图3（b ）所示.由图3可知，数值解和精确解是一致的.（a）精确解（b）数值解图3温度分布（n =40，m =10）当m =10时，随着计算规模不断增大，VRP-GMRES （m ）算法所需迭代次数变化较小且所需的迭代次数要比GMRES （m ）少很多，如图4（a ）所示，说明VRP-GMRES （m ）算法有更高的计算效率，同时，VRP-GMRES （m ）算法还有更高的精度，如图4（b ）所示.另外，实际执行VRP-GMRES （m ）算法时，虽然每次迭代所耗时可能比GMRES （m ）算法长，但是由于VRP-GMRES （m ）算法收敛速度很快，所以当残量范数达到给定误差时，如表5所示，本文提出的VRP-GMRES （m ）算法总的运行时间要比GMRES （m ）算法少很多.白雪婷，等：解线性方程组的VRP-GMRES （m ）迭代法2021年第4期学报（a）计算效率比较（b）计算精度比较图4不同网格下两种算法计算效率和计算精度比较（m =10）表5不同网格下两种算法运行时间比较n （网格数）405060708090m（重启动参数）101010101010两种算法运行时间/s GMRES （m ）算法1.5808475.70255516.96530643.204335100.077638189.671624VRP-GMRES （m ）算法0.8298662.4452352.44523514.07231827.73167451.9084184结语文中提出一种求解线性方程组的VRP-GMRES （m ）算法，理论证明新算法收敛且计算精度更高.数值试验结果表明本文提出的VRP-GMRES （m ）算法不仅有更高的计算效率和计算精度，而且有更好的稳定性.新算法适合用来求解由科学研究和工程问题得到的大型线性方程组.参考文献：［1］PHILIPPEON B ，REICHEL L.The generation of Krylov subspace bass ［J ］.Appl.Numer.Math.，2012，62：1171-1186.［2］罗东明，陈平剑，吴希明.GMRES 算法在悬停旋翼数值模拟中的应用［J ］.空气动力学报，2012，30（4）：471-476.［3］戴愚志，宋竞正，任慧龙.GMRES 方法在悬停旋翼数值模拟中的应用［J ］.海洋工程，2003，21（4）：15-22.［4］PU B Y ，HUANG Y Z ，WEN C.A Preconditionedand Extrapolation-accelerated GMRES Method for Page Rank ［J ］.Appl Math Lett ，2014，37：95-100.［5］SAAD Y ，SCHULTZ M H.GMRES ：A General⁃ized Minimal Residual Algorithm for Solving Nonsymmet⁃ric Linear Systems ［J ］.SIAM J Sci Comput ，1986，7（3）：856-869.［6］AYACHOUR E H.A Fast Implementation forGMRES Method ［J ］.Comput Appl Math ，2003，159：269-283.［7］JOSE E P ，ALEX A P.Making use of BDE-GMRESmethods for solving short and long-term dynamics in power systems ［J ］.Elec Power Energy Sys ，2013，45：293-302.［8］YIN J F ，KEN H.Preconditioned GMRES Meth⁃ods with Incomplete Givens Orthogonalization Method for Lagre Sparse Least-squares Problems ［J ］.Compu ApplMath ，2009，226：177-186.［9］LIN F R ，YANG S W ，JIN X Q.PreconditionedIterative Methods for Fractional Diffusion Equation ［J ］.J Comput Phys ，2014，256：109-117.［10］LIANG Y ，SZULARZ M ，YANG L T.Finite-ele⁃ment-wise Domain Decomposition Iterative Solvers with Polynomial Preconditioning ［J ］.Math Comput Mod ，2013，58：421-437.［11］BAKE A H.On Improving the Performance ofthe Linear Solver Restarted Gmres ［D ］.Boulder ：University of Colorado at Boulder ，2003：20-25.［12］BAKER A H ，JESSUP E R ，KOLEV T V.ASimple Strategy for Varying the Restart Parameter inGMRES（m）［J］.J Comput Appl Math，2009，230：751-761.［13］PEAIRS L，CHEN T ing Reinforcement Learning to Vary the m in GMRES（m）［J］.Procedia Com⁃puter Science，2011（4）：2257-2266.［14］ESSAI A.Weighted FOM and GMRES for Solv⁃ing Nonsymmetric Linear Systems［J］.Numer Algorithms，1998，18：277-299.［15］蔡大用，白峰杉.高等数值分析［M］.北京：清华大学出版社，1997：74-75.（责任编辑：陈衍峰）A Kind of VRP-GMRES(m)Iteration Algorithm for Linear EquationsBAI Xue-ting，YANG Qin-le（Jinzhong University of Information，Jinzhong030800，China）Abstract：To solve large scale linear equations in scientific computations and engineering applications eff⁃ciently，an iterative method named VRP-GMRES(m)algorithm is proved.By properly changing a variable restart parameter for the GMRES(m)algorithm，the iteration stagnation problem resulted from improper selection of the parameter is resolved efficiently.Givens orthogonal transformation is used to prove that the proposed algorithm is not only fast convergent but also is highly accurate.Numerical experiments show that the new algorithm can significantly improve the computational efficiency and precision.Its superiori⁃ties will be much more remarkable when it is used to solve larger scale problems.So it has extensive pros⁃pect in scientific and engineering computing.Keywords：VRP-GMRES(m)algorithm；Givens transformation；variable parameter；convergence；compu⁃tational accuracy白雪婷，等：解线性方程组的VRP-GMRES（m）迭代法。

高斯-赛德尔迭代法例题高斯-赛德尔迭代法是一种用于解线性方程组的迭代方法。

它通过不断更新变量的值来逼近方程组的解。

以下是一个使用高斯-赛德尔迭代法求解线性方程组的例题：考虑以下线性方程组：```2x + y + z = 9x + 3y + z = 10x + y + 4z = 16```我们可以将方程组表示为矩阵形式：```| 2 1 1 | | x | | 9 || 1 3 1 | x | y | = | 10 || 1 1 4 | | z | | 16 |```迭代的过程如下：1. 选择一个初始解向量，比如x=0, y=0, z=0。

2. 使用迭代公式进行更新：-更新x 的值：x_new = (9 - y - z) / 2-更新y 的值：y_new = (10 - x_new - z) / 3-更新z 的值：z_new = (16 - x_new - y_new) / 43. 重复步骤2，直到解向量的值收敛于方程组的解。

假设我们进行3次迭代，初始解向量为x=0, y=0, z=0。

则迭代的过程如下：1. 第一次迭代：-更新x 的值：x_new = (9 - 0 - 0) / 2 = 4.5-更新y 的值：y_new = (10 - 4.5 - 0) / 3 ≈1.83-更新z 的值：z_new = (16 - 4.5 - 1.83) / 4 ≈2.422. 第二次迭代：-更新x 的值：x_new = (9 - 1.83 - 2.42) / 2 ≈2.87-更新y 的值：y_new = (10 - 2.87 - 2.42) / 3 ≈1.9-更新z 的值：z_new = (16 - 2.87 - 1.9) / 4 ≈2.813. 第三次迭代：-更新x 的值：x_new = (9 - 1.9 - 2.81) / 2 ≈1.65-更新y 的值：y_new = (10 - 1.65 - 2.81) / 3 ≈1.85-更新z 的值：z_new = (16 - 1.65 - 1.85) / 4 ≈3.14经过3次迭代后，解向量的值接近于x ≈ 1.65, y ≈1.85, z ≈3.14，这就是方程组的近似解。

仿真平台与工具应用实践Jacobi迭代法求解线性方程组^实验报告：院系：专业班级：姓名：学号：指导老师：}一、 ;二、 实验目的熟悉Jacobi 迭代法原理；学习使用Jacobi 迭代法求解线性方程组；{编程实现该方法；三、 实验内容应用Jacobi 迭代法解如下线性方程组：,⎪⎩⎪⎨⎧=++--=+-=+-1552218474321321321x x x x x x x x x ，要求计算精度为710-四、 ^五、 实验过程（1）、算法理论Jacobi 迭代格式的引出是依据迭代法的基本思想：构造一个向量系列(){}n X ，使其收敛至某个极限*X ，则*X 就是要求的方程组的准确解。

Jacobi 迭代将方程组： ⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++nn nn n n n n n n b x a x a x a b x a x a x a b x a x a x a22112222212111212111 )1(~在假设0≠ii a ，改写成()⎪⎪⎩⎪⎪⎨⎧++++=++++=++++=--n n n n n n n n n n n g x b x b x b x g x b x b x b x g x b x b x b x 112211223231212113132121 )2( 如果引用系数矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=nn n n a a a a A 1111，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0011 n n b b B 及向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=n x x X 1，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=n b b b 1，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=n g g g 1， 方程组（1）和（2）分别可写为：b AX =及g BX X +=，这样就得到了jacobi 迭代格式01g BX X k k +=+用jacobi 迭代解方程组b AX =时，就可任意取初值0X 带入迭代可知式g BX X k k +=+1，然后求k k X ∞→lim 。