基于MATLAB的混沌序列图像加密算法的研究的开题报告
- 格式:doc
- 大小:41.00 KB
- 文档页数:11

基于混沌系统的图像加密技术研究混沌系统是一种具有无序、随机和不可预测性质的非线性动力学系统,其在密码学中已被广泛应用于消息加密、图像加密、身份验证等领域。
其中,基于混沌系统的图像加密技术可以实现在保持加密数据安全性的同时,保留了图像的视觉效果,因此更适用于图像通信和存储方面。
一、混沌系统的基本原理混沌系统是一种迭代映射动力学系统,在非线性条件下,其状态会随时间变化而呈现出随机、无序、分岔和周期皓等性质。
混沌系统可以用数学模型来描述,其中最著名的混沌系统是洛伦兹系统,它用于描述大气科学中的对流流体的运动。
依据混沌系统的特性,现代密码学发展了一系列混沌加密算法,其中最为常用的是混沌置换和混沌流密码。
混沌置换算法是一种基于迭代映射的分组密码算法,随机的迭代次数和初始条件可用于扰乱图像像素,从而达到加密的目的。
混沌流密码则是利用混沌序列产生伪随机数流,用于对原始数据进行加密。
二、基于混沌系统的图像加密技术图像加密技术是在数字图像传输和存储时必不可少的技术手段。
其中,基于混沌系统的图像加密技术相比于传统的加密技术,更适用于图像加密,具有快速、高效、安全等优势。
下面将从两个方面介绍基于混沌系统的图像加密技术。
1、基于混沌置换的图像加密技术混沌置换算法将迭代映射应用在了像素排序上,通过对图像像素位置的随机变换,来实现混沌加密。
将图像像素坐标变换为一个混沌序列,再通过混沌序列的迭代计算,洛伦兹混沌序列产生了一个随机序列,用于对图像的像素进行混沌置换,从而实现图像的加密。
具体的实现过程为:首先,将图像转化为一维数组,并设置一组初始条件。
然后,通过迭代计算混沌序列,从而得到像素位置的一个置换序列;接着,采用该序列对图像像素进行混淆;最后,将加密后的像素重新排列成二维矩阵,即完成了图像加密。
2、基于混沌流密码的图像加密技术混沌流密码是利用混沌序列产生伪随机数流,用于对原始数据进行加密的密码算法。
混沌流密码包括两个主要部分:混沌序列发生器和异或加密器。

基于混沌的图像加密算法研究图像加密算法是信息安全领域中的重要研究方向之一,它通过对图像进行加密和解密操作,实现保护图像隐私和安全传输等目的。
本文将重点探讨基于混沌的图像加密算法的研究,分析其原理、优势和应用场景。
首先,我们来了解一下混沌理论。
混沌理论是一种非线性动力学系统的研究分支,其在计算机科学和密码学领域有着广泛的应用。
混沌系统具有随机性、不可预测性和灵敏性等特点,这使得混沌可作为图像加密算法的基础。
基于混沌的图像加密算法主要包括两个部分,即混沌映射和置乱操作。
混沌映射是将图像像素映射到一个混沌的迭代序列上,而置乱操作则通过对混沌序列进行重新排列实现对图像的置乱加密。
下面我们将详细介绍这两个部分。
首先是混沌映射。
混沌映射通常选取经典的混沌系统,如Logistic映射和Henon映射等作为基础。
这些映射具有高度的不可预测性和混沌性质,适用于图像加密。
在加密过程中,首先将图像像素值归一化到[0,1]的范围内,然后通过混沌映射将像素值映射到一个混沌序列上。
通过迭代映射操作,可以得到一个与原图像无关的混沌序列。
这个序列将作为后续置乱操作的密钥,确保了加密的随机性和安全性。
接下来是置乱操作。
在加密过程中,通过对混沌序列进行重新排列,实现对图像像素的混乱置乱。
最常用的方法是基于Arnold置乱算法和Baker映射置乱算法。
Arnold置乱算法是一种二维置乱算法,通过对图像像素的行列位置进行迭代映射操作,实现像素位置的混乱。
而Baker映射置乱算法则是通过对图像像素进行乘积操作,实现图像像素值的混乱。
这两种置乱算法具有较高的随机性和不可逆性,能够有效地保障图像的安全性。
基于混沌的图像加密算法具有以下优势:第一,混沌映射和置乱操作具有高度的随机性和不可线性特征,使得加密过程中产生的密钥和置乱后的图像难以被破解和恢复。
这大大增强了图像的安全性。
第二,基于混沌的图像加密算法具有较好的抗攻击性。
混沌系统的不可预测性和随机性能够防止统计分析和密码分析等攻击手段。


哈尔滨理工大学硕士学位论文基于混沌理论的数字图像加密算法的研究姓名:孙广明申请学位级别:硕士专业:控制理论与控制工程指导教师:吕宁20090301哈尔滨理T人学下学硕lj学位论文基于混沌理论的数字图像加密算法的研究摘要随着计算机技术和网络技术快速发展,信息在社会中的地位和作用越来越重要,网络信息安全与保密问题显得愈发重要和突出,信息安全已成为信息化社会重要与关键问题之一。
数字图像作为一种特殊的数字信息的存在方式,如何有效的保证其数字信息的机密性、完整性、可用性、可控性和不可抵赖性是当前信息安全技术研究领域的重要研究方向。
混沌现象是非线性动态系统中出现的确定性的伪随机过程,其具有非周期性、遍历性、伪随机性及对初值的敏感性,与加密系统二者之间存在着许多相似之处,目前研究基于混沌理论的保密通信、信息加密和信息隐藏技术是非线性科学和信息科学两个领域交叉融合的热点问题之一。
本文重点研究了数字图像的信息安全问题,着重研究了数字图像加密的方法,论文的主要工作及成果如下:1.在对密码学和混沌系统基本理论进行讨论分析的基础上,重点研究了密码学和混沌系统的联系及构造混沌分组密码的方法。
2.对定义在(O,1)上的混沌移位映射特性进行了分析,将混沌序列引入图像加密算法中,据此提出一种基于混沌移位映射的数字图像加密算法,通过实验验证了该算法的安全性。
3.对于混沌系统数字化后引起的混沌性能下降,构造了一种结合Logistic映射和分段线性混沌映射(PLCM)及定义在(0,1)上的移位映射设计了一个多混沌系统的随机数发生器,具有良好的随机性和在有限精度实现条件下周期大的特点;基于提出的混沌随机数发生器提出了一种分组图像加密算法,该算法具有较强的鲁棒性及抗攻击免疫能力,加密图像在部分受损或缺失后,仍有较好的恢复效果。
4.将混沌系统和分组密码链接(CBC)模式相结合,提出一种数字图像自适应加密算法。
利用图像本身所携带的信息实现图像自适应加密,同时克服了混沌系统数字化用于图像加密系统带来的周期性。

实验项目与实验报告(1 )学科:信息与网络安全学号::羊波时间:11月3 日DD=sy/sx %置乱度global M;global N;global Ximage;global Yimage;key1=input('请输入密钥key1:');key=4;for(i=1:M)for(j=1:N)key1=key*key1*(1-key1);a(i,j)=key1;endendkey2=input('请输入密钥key2:');for(i=1:M)for(j=1:N)key2=key*key2*(1-key2);b(i,j)=key2;endendx=0.4*a+0.6*b;e=round(x*256);tt=0.01;Zimage=(Yimage-(1-tt)*e)/tt;figure(5)imshow(Zimage,[]);加密过程:①首先将要加密的图片test.gif保存在d盘中,如下图1所示:图1存在d盘中的test图片②打开Matlab软件并把上面的加密程序输入软件环境窗口,如下图2所示:图2在Matlab中输入的编程③程序输入完成后,按回车键,程序会运行得出5图片,分别为加密前的原图和加密后的图片、加密前的直方图和加密后的直方图。
如下图3、图4、图5、图6所示:图3加密前的原图图4加密后的图片图5加密前的直方图图6加密后的直方图说明:加密后的灰度直方图分析可以用来衡量加密算法的扰乱性。
上图3、图4、图5、图6是加密前后的图像以及它们的直方图的对比。
可见,加密后的直方图呈均匀分布,未保留任何明文信息。
图6加密后的直方图的图像越均匀说明混沌效应越好,上图6总体上来说是均匀的,只是在编程的时候考虑的只是黑白色的点,所以直方图看起来全部的点不是绝对的均匀。
解密过程:⑦如果想得到原图(解密),必须在MATLAB界面窗口输入两个密钥,“请输入密匙key1:0.1 请输入密匙key2:0.2”;如下图7所示:图7解密之后得到的原图从上图可以看出,加密后的图像没有留下原图的痕迹,而解密后的图像看不出差别,此方法加密效果良好。
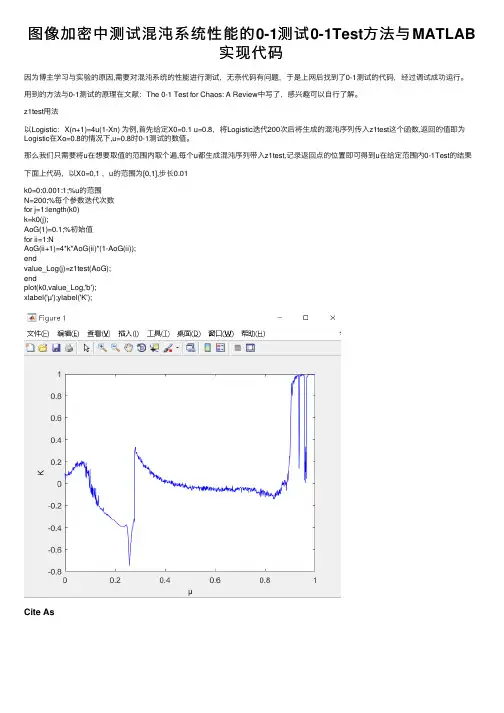
图像加密中测试混沌系统性能的0-1测试0-1Test⽅法与MATLAB
实现代码
因为博主学习与实验的原因,需要对混沌系统的性能进⾏测试,⽆奈代码有问题,于是上⽹后找到了0-1测试的代码,经过调试成功运⾏。
⽤到的⽅法与0-1测试的原理在⽂献:The 0-1 Test for Chaos: A Review中写了,感兴趣可以⾃⾏了解。
z1test⽤法
以Logistic:X(n+1)=4u(1-Xn) 为例,⾸先给定X0=0.1 u=0.8,将Logistic迭代200次后将⽣成的混沌序列传⼊z1test这个函数,返回的值即为Logistic在Xo=0.8的情况下,u=0.8时0-1测试的数值。
那么我们只需要将u在想要取值的范围内取个遍,每个u都⽣成混沌序列带⼊z1test,记录返回点的位置即可得到u在给定范围内0-1Test的结果下⾯上代码,以X0=0,1 ,u的范围为[0,1],步长0.01
k0=0:0.001:1;%u的范围
N=200;%每个参数迭代次数
for j=1:length(k0)
k=k0(j);
AoG(1)=0.1;%初始值
for ii=1:N
AoG(ii+1)=4*k*AoG(ii)*(1-AoG(ii));
end
value_Log(j)=z1test(AoG);
end
plot(k0,value_Log,'b');
xlabel('µ');ylabel('K');
Cite As。


基于混沌理论的图像加密技术研究随着数字技术的发展,人们越来越依赖数字图像来实现信息的传递和存储,而数字图像的信息安全性也变得越来越重要。
因此,图像加密技术逐渐成为了保障数字信息安全的一个重要手段。
其中一种常用的加密方法是基于混沌理论的图像加密技术。
混沌是指非线性动力学中的一种现象,其特点是系统的状态随时间的推移呈现无规律、复杂、难以预测的特性。
混沌理论被广泛应用于信息加密领域,可以通过自身的无规律性有效保护图像信息。
基于混沌理论的图像加密技术的主要思路是将其分为两个步骤:加密和解密。
加密过程中,通过混沌发生器产生密钥流,再对原始图像进行置乱和扰动操作,最后加上密钥流得到密文。
解密过程中,则是通过同样的密钥流,反向进行置乱和扰动操作得到原始图像。
在实际应用中,混沌发生器的选择十分重要。
目前,常用的混沌发生器有一维混沌映射发生器和二维混沌映射发生器。
一维混沌映射发生器可以用于生成一维的密钥流序列,例如Logistic映射发生器、Henon映射发生器、Tent映射发生器等。
二维混沌映射发生器则可以用于生成二维矩阵型的密钥流序列,例如Arnold映射、Cat映射等。
其中,Arnold映射是一种经典的二维混沌映射发生器,其主要实现过程是先进行像素重排,再进行置换操作。
这种操作能够在不改变图像内容的情况下,使得图像的灰度值位置发生随机变化。
同时,其具有一定的可加密性,可以通过调整参数提高其加密强度。
除了混沌发生器的选择以外,置乱和扰动操作的设计也是图像加密技术中的重要问题。
置乱操作一般包括像素重排、行列置换和旋转等操作,其目的是将原始图像的像素位置打乱,让其看起来像是被随机排列过的。
扰动操作则是对图像进行一系列的变换操作,使得图像具有一定程度的随机性,从而增加了加密的难度。
常用的扰动操作包括灰度变换、像素异或以及高斯噪声添加等。
值得注意的是,虽然基于混沌理论的图像加密技术具有一定的优势,但其其也存在着一些缺陷。

基于混沌动力学的图像加密算法研究近年来,信息安全已经成为了社会各个领域中备受关注的问题。
在数字图像传输和存储过程中,保护图像的机密性就显得尤为重要。
为了解决这个问题,图像加密算法应运而生。
在早期的图像加密算法中,我们常常会使用基于互换的方法,例如置换或替换等。
这些方法可以使加密的图像看起来像一堆随机像素,但往往容易被恢复出原始图像。
随着计算机技术和密码学的发展,基于非线性动力系统的图像加密算法逐渐受到更广泛的关注。
混沌动力学依赖于确定性混沌的原理,由此可以产生看似随机的数列。
这种混沌的特性,使得它在图像加密领域中得到了广泛的应用。
基于混沌动力学的图像加密算法采用了一些经典的加密方法,例如置换和替换等,同时引入了混沌动力学系统中的变量,以此增加加密的难度。
在基于混沌动力学的图像加密算法中,通常采用了一些经典的混沌映射,例如Logistic映射和Henon映射等。
这些映射具有周期性,非周期性以及混沌性等不同的属性,因此可以根据不同的加密需求来选择不同的映射函数。
在加密的过程中,加密者首先会将明文图像拆分成一系列的像素点。
然后,使用混沌映射对该像素点序列进行置换操作,接着再使用像素级别的代替方法(Substitution)进行加密。
最后,通过混合算法对加密后的图像进行输出处理。
在基于混沌动力学的图像加密算法中,解密过程与加密过程相反。
解密者根据混沌映射的参数和密钥,可以对加密后的图像进行还原,得到原始的明文图像。
相比于传统的加密算法,基于混沌动力学的图像加密算法在加密效果和安全性方面都具有显著的优势。
由于混沌映射的特性,再加上像素置换和代替的方法,使得加密后的图像难以被解密得到原始的明文图像,从而达到了良好的保密性。
混沌动力学的图像加密算法还具有高速性和高效性的特点。
在加密过程中只需要对像素点矩阵进行简单的变换操作,这种操作速度非常快。
同时,算法的可靠性和可扩展性也极高,因此可以很好地应用于大规模的图像加密领域中。

基于混沌的图像加密与解密算法研究随着科技的不断发展,网络通信与信息传输已经成为了人们生活中必不可少的一部分。
而在这些通讯过程中,保密性与安全性是必须要考虑的一个因素。
如果信息在传输过程中被他人窃取或篡改,那么造成的后果将是不可估量的。
因此,加密算法就成为了保障信息安全的一个重要手段。
在保障信息安全这个过程中,加密算法的安全性被认为是至关重要的。
一般来说,加密算法的安全性是指在未知密钥情况下,即使攻击者拥有了大量加密数据,也不能破解加密算法,从而获得明文的过程。
而目前基于混沌现象的图像加密算法应用越来越广泛,主要由于其高效、强大的随机性和不可复制性。
那么,什么是混沌?简单来说,混沌是一种在确定性条件下出现的随机性现象。
即体现出完全随机性的样子,但是却有规律可言,具有不可预测性和不可复制性,因此我们可以运用混沌现象进行加密。
基于混沌的图像加密算法,是一种基于混沌现象加密技术的图像保护技术,它通过在两个加密轮中融合Lorenz混沌系统、Arnold变换和置乱加密方式,来保护原始的图像信息。
其优点在于具有高保密性、鲁棒性强、隐藏效果好等优点。
不仅如此,这种加密方式也可以应用于数字音频、视频等数据的加密保护中,使得加密通信具备鲁棒性、隐秘性和可扩展性等特点。
具体来说,基于混沌的图像加密算法的实现可以分为以下几个步骤:第一步是混沌序列生成。
混沌序列的生成是加密算法中最重要的部分,其目的是生成一个不可预测的伪随机序列。
混沌序列通常是由某种混沌系统产生的,其中最常用的混沌系统为Lorenz系统,该系统可以产生不可预测的随机序列。
第二步是Arnold变换。
Arnold变换是一种置换变换,它将原始的图像通过矩阵运算进行重组,使其成为一个加密状态。
通过Arnold变换,原始图像的像素被重新安排在了一个特定的顺序里,从而保证了加密性。
第三步是置换加密。
置换是通过将加密后的图像像素位置进行随机置换来增加加密难度。
原始图像像素的置换序列可以通过混沌序列进行生成,而变换后的图像像素位置可以通过这个序列得到。

本科毕业论文题目:基于Matlab的光学图像加密解密技术院(部):理学院专业:光信息科学与技术班级:光信122姓名:韩硕学号:20121212082指导教师:王惠临完成日期:2016年6月4日目录摘要 (IV)ABSTRACT (V)1前言 (1)1.1 选题背景及意义 (1)1.2 Matlab软件介绍 (1)1.3 Matlab的主要特点 (2)1.4 本文结构安排 (3)2基于Matlab进行图形图像处理基础 (4)2.1 Matlab中图形图像的分类 (4)2.1.1 索引图像 (4)2.1.2 灰度图像 (4)2.1.3 RGB图像 (4)2.1.4 二值图像 (4)2.2 Matlab常用的图形图像处理函数(命令) (4)3图形图像的加密解密技术 (6)3.1 图形图像加密传输理论框图以及图形图像加密特点 (6)3.2 置乱加密技术 (7)3.2.1 随机打乱各层的行或列 (7)3.2.2 像素点随机打乱 (12)3.2.3 像素点RGB值的放大 (14)3.2.4 灰度变换置乱 (16)3.3 基于混沌的图像加密解密技术 (17)3.3.1 混沌加密原理 (17)3.3.2 用Matlab的实现基于混沌的图像置乱加密算法 (18)3.4 基于秘密分割加密解密技术 (20)3.4.1 秘密分割加密算法的原理 (20)3.4.2秘密分割加密算法的Matlab实现 (20)4结论 (24)4.1 总结 (24)4.2 展望 (24)谢辞 (26)参考文献 (27)摘要社会在进步,时代在发展,计算机技术在飞速发展,互联网技术也在日益进步,各种迹象都表明着我们已经进入了一个信息大爆炸的时代。
人们每天通过互联网获取大量的数字图像的信息,然而在信息的传送中,未经加密的原始的数据非常容易遭受非法途径的截取并被恶意更改。
因此,互联网时代如何确保图像信息安全传送越来越受到人们的重视。
基于此,也提出了不少图形加密解密的算法。
基于混沌系统的图像加密算法实现混沌系统作为一种复杂的非线性动力学系统,近年来受到了广泛的关注。
其特点在于具有高度的敏感性依赖于初值,且能够呈现出高度随机的行为。
因此,在信息安全领域,混沌系统被广泛应用于加密通信、图像加密等方面。
本文将讨论基于混沌系统的图像加密算法及其实现方法。
一、混沌加密算法的优点基于混沌系统的加密算法具有以下几个优点:1.高度随机性:混沌系统能产生高度随机的序列,使其成为一种理想的加密源。
2.异常敏感性:混沌系统依赖于初始状态,因此对于不同的初始状态会得到完全不同的结果,异常敏感性是其最大的特点之一。
3.实时性:混沌系统产生的随机序列是实时的,可以使加密的过程立即执行,不会对通信速度产生影响。
二、混沌加密算法的实现方式1.图像灰度值的混沌加密对图像进行加密的方法之一是利用混沌序列对图像的灰度级进行加密。
具体步骤如下:(1)采用混沌系统生成长度为n的随机数列,作为灰度级的加密密钥;(2)将原始图像的灰度级进行拆分,对每一个像素值进行加密运算,得到加密后的图像。
实现的原理是通过将原始图像的灰度级与密钥进行异或操作,得到加密后的灰度级,再重新生成图像。
该方法简单易懂,实用性强,但其加密强度较低,容易遭受肉眼可见的攻击。
2.图像的置换加密该加密算法采用混沌映射生成随机序列,对矩阵的位置进行加密。
具体步骤如下:(1)将图像像素矩阵进行分组;(2)采用混沌映射生成随机序列,将序列值范围归一化到数组[1, N]以便做下标;(3)通过随机序列将矩阵进行排列,得到加密后的图像。
实现的原理是采用置换加密方法,即通过混沌映射产生的随机数,来改变图像像素的位置,从而构造加密后的图像。
该方法加密强度较高,但实现较为复杂,不适用于实时加密。
3.图像像素值的加密该加密算法采用混沌系统产生随机序列,对原始图像的像素值进行加密。
具体步骤如下:(1)采用混沌系统生成噪声序列,作为图像的加密解密密钥;(2)将原始图像的像素值与密钥进行运算,得到加密后的像素值。
基于混沌映射的图像加密算法研究第一章:引言随着信息技术和网络技术的发展,图像的存储和传输已经成为了一项极其重要的任务。
在这样的背景下,保护图像信息的安全性也变得尤为重要。
为了解决这个问题,图像加密算法应运而生。
目前,混沌映射已成为图像加密领域中的一个热门研究方向,该算法通过利用混沌的性质对图像进行加密,可以有效地保护图像的安全性。
因此,本文将探讨基于混沌映射的图像加密算法研究。
第二章:混沌理论混沌指的是一类看似无序、但却有规律的非线性动力学系统。
混沌的最主要特征是敏感依赖于初始条件,也就是说,对于具有微小初始变化的系统,输出结果将会有相对较大的差异。
混沌的理论奠定了现代密码学的基础。
利用混沌所具有的复杂性和不可预测性,可以很好地实现对信息的加密和解密。
第三章:基于混沌映射的图像加密算法3.1 图像加密流程基于混沌映射的图像加密算法的基本流程如下:(1)准备密钥:密钥是进行加密和解密所必须的参数,是加密算法的核心部分。
通过混沌映射算法生成一组密钥,用于对原图进行加密。
(2)图像预处理:为了提高加密强度,可以对原图进行预处理,比如图像分块、灰度变换等。
(3)混沌加密:将原图按照一定的规则进行分散扰乱,并使用密钥进行加密,最终生成一个密文图像。
(4)密文传输:将加密完成的密文传输给接收方。
(5)密文解密:接收方通过解密密钥将密文图像解密还原成明文图像。
3.2 混沌映射算法选择混沌映射算法的选择对于图像加密的结果有着至关重要的影响。
常见的混沌映射算法包括Logistic映射、Henon映射、Tent映射、Ikeda映射等。
各种混沌映射算法具有不同的数学特性和加密效果,不同的应用场景需要选择不同的混沌映射算法。
比如,Tent映射和Logistic映射适用于对灰度图像加密,而Henon和Ikeda映射适用于对彩色图像加密。
3.3 密钥生成算法密钥生成算法是混沌图像加密算法的核心部分,是系统安全性的基石。
密钥生成算法需要利用混沌映射产生的随机序列生成密钥,以确保加解密双方使用的密钥的随机性和唯一性。
基于混沌算法的图像加密与解密研究近年来,随着信息技术的飞速发展和互联网应用的普及,隐私数据的保护变得尤为重要。
图像加密作为保护图像隐私的一种常用手段,受到了广泛关注。
混沌算法作为一种具有高度随机性和无周期性的灵活算法,被广泛应用于图像加密与解密领域。
本文将重点研究基于混沌算法的图像加密与解密技术,并探讨其在实际应用中的潜在优势和挑战。
首先,我们将介绍混沌算法的基本原理和特点。
混沌算法是一种在非线性动力学系统中出现的随机现象,其离散时间动态方程描述如下:x_(n+1) = f(x_n) 公式(1)其中 x 为状态变量,f 为一个非线性映射函数。
混沌算法的主要特点是初始条件和参数对最终结果产生巨大影响,对于微小的改变输入条件,会产生截然不同的输出结果。
基于混沌算法的图像加密和解密技术借鉴了上述的特点,通过将图像的像素值与混沌序列进行异或运算或置换操作,来达到加密的目的。
其中,像素值与混沌序列进行异或运算的操作是常见的加密模式。
这种加密方式可以使得加密后的图像在零交叉点上分布均匀,增强了加密的随机性。
同时,加密和解密使用相同的混沌序列作为密钥,可以简化加密和解密的过程。
接下来,我们将详细讨论基于混沌算法的图像加密和解密方法。
首先是基于混沌序列的图像置乱算法。
在这种方法中,混沌序列生成器作为密钥发挥关键作用。
首先,对图像进行象素重排,然后将混沌序列与图像进行异或运算。
在解密过程中,同样需要首先对图像进行像素重排,然后通过混沌序列与密文进行异或运算得到原始图像。
其次是基于混沌序列的图像加密算法。
在这种算法中,混沌序列的值与图像的像素值进行异或运算,然后通过再次应用混沌序列对加密后的图像进行置乱操作。
解密过程通过相同的混沌序列对密文进行逆操作来还原原始图像。
此外,对混沌算法进行改进和优化也是图像加密与解密研究的一个重要方向。
传统的混沌序列生成器存在周期性和低随机性的问题,可能导致加密算法的安全性下降。
因此,研究人员通过改进混沌映射函数、增加参数等方式来提高混沌序列的随机性和无周期性特点,从而提升图像加密的安全性。
基于混沌映射的高效图像加密算法研究一、引言图像加密算法是图像信息安全保障的重要手段之一。
随着数字图像在网络传输、存储和处理中的广泛应用,图像安全性越来越受到人们的关注。
基于传统加/解密技术,因为其有规律性和可逆性,存在易被破解的风险,而基于混沌映射的图像加密算法在信息保障领域具备了越来越重要的地位。
二、混沌映射混沌现象是19世纪末出现的,在引力理论、随机噪声、大气环流、金融市场波动、生物生长等各个领域都有应用。
其中,混沌映射因为其非线性、随机性、灵敏性和分形属性,被广泛运用在密码学中。
在密钥的选择和加密环节中,算法使用一个巨大的迭代过程,基于初始值系列和一个所谓的“干扰项”,生成了高度的混沌序列。
然后,密钥和加密信息都从产生的混沌序列中获取。
混沌映射的关键在于对数据的前后顺序和位重组进行处理。
三、基于混沌映射的高效图像加密算法(1)基本概念:基于混沌映射的高效图像加密算法是指依据混沌映射理论,通过特定的算法将明文图像转化为了经过加密处理后的密文图像的一组流程。
(2)加/解密流程:1)密钥初始化:初始化算法的两个密钥,一个为图像密钥,一个为控制端口的密钥,两个密钥都采用混沌映射生成。
2)图像加密:在该步骤中,明文图像首先被分成若干个等大小的块,然后对每个块内部进行加密。
加密的过程包括:像素重排、混沌映射和异或操作。
其中,像素重排和随机重组都可以在保证混沌映射密序列前后顺序无规律的情况下,增加加密强度。
3)图像解密:在该步骤中,密文图像首先被分成若干个等大小的块,每个块内部解密。
解密的流程与加密的流程是对称的。
(3)加密实现:主要采用MATLAB平台搭建,实现,同时考虑编程的简洁和运算效率。
1)实现功能:对加密指令、输出、解密指令等具有良好的可读性和易用性。
2)实现细节:由于工作的特殊性,需要注意的事项包括:混沌映射算法、图像块分组与序列重排,各个变量、数组的规划、初始化和调用。
四、实验结果及分析通过实验,取得了以下结论:(1)在采取合理的物理模型、工具和手段的基础上,基于混沌映射的高效图像加密算法可以实现信息加密的目的。
基于混沌映射的图像加密算法研究一、引言信息安全是当今社会中非常重要的一个领域,尤其是在数字化信息技术日益发展的今天,随着信息技术的不断进步,各种网络攻击的手段也越来越多,而信息加密技术也逐渐变得越来越重要。
为了保护信息的隐私和安全,需要使用一些加密算法来对其进行加密。
二、混沌映射混沌理论起源于科学领域,它是一种非线性、动态的系统,这种系统不易受外界干扰,十分敏感,且在短时间内变化难以预测,具有随机性和不可预测性。
混沌映射是一类具有混沌特性的映射,其实现是通过非线性迭代函数来实现的,由于其可靠性和安全性的特点,混沌映射被广泛运用于密码学领域中,特别是在图像加密领域中的应用更为广泛。
三、基于混沌映射的图像加密算法图像加密算法并不局限于某一个特定的加密技术,它可以采用多种加密技术来保护图像的隐私和安全,其中基于混沌映射的图像加密算法是一种比较优秀的图像加密技术。
该加密算法的基本思路是将明文图像映射到一个混沌空间中,然后对该混沌空间进行加密,最后将加密后的混沌空间映射回原明文图像,从而实现了图像的加密。
具体的加密步骤如下:1. 映射图像数据至混沌空间:选取适当的混沌映射函数,将明文图像数据映射至混沌空间。
2. 加密混沌空间:采用一些加密技术对混沌空间进行加密处理。
3. 映射混沌空间至图像数据:将加密后的混沌空间映射回原明文图像。
这种加密算法采用混沌映射的不可预测性和随机性来进行加密,有效地保护了图像的安全性,且加密过程简单、易于实现。
四、针对该算法的攻击但基于混沌映射的图像加密算法也并非完全安全可靠的。
一些攻击者可以通过一些手段来解密加密后的混沌空间,并从中获取明文图像数据。
这些攻击方式有以下几种:1. 文字模式攻击:通过获取足够多的加密数据,或者使用已知的密钥,在没有进行解密操作的情况下,将混沌空间中的一部分数据与密钥一一比对,从而破解混沌空间的加密。
2. 图像直观攻击:通过对加密后的图像空间进行变化,比如对图像进行旋转、翻转等操作,从而获取一些关键部位的信息,进而破解混沌空间的加密。
吉林农业大学
本科毕业设计开题报告
课题名称:基于MATLAB的混沌序列图像加密算法的研究
学院(系):信息技术学院
年级专业:2009级电子信息科学与技术2班
学生姓名:XX
指导教师:刘媛媛
完成日期:2013年2月27日
目录
一、设计目的及意义 (3)
二、研究现状 (3)
三、设计内容 (3)
四、开发环境 (3)
五、分析设计 (3)
1、设计要求 (3)
2、设计原理 (3)
3、涉及到的程序代码 (4)
4、主要思想 (6)
六、结果及分析 (6)
1、运行示例 (6)
2、结果评估 (8)
七、参考文献 (9)
八、研究工作进度 (10)
一、设计目的及意义
熟练使用matlab运用matlab进行编程,使用matlab语言进行数据的隐藏加密,确保数字图像信息的安全,混沌序列具有容易生成,对初始条件和混沌参数敏感等特点,近年来在图像加密领域得到了广泛的应用。
使用必要的算法将信息进行加解密,实现信息的保护。
二、研究现状
随着Internet技术与多媒体技术的飞速发展,数字化信息可以以不同的形式在网络上方便、快捷地传输。
多媒体通信逐渐成为人们之间信息交流的重要手段。
人们通过网络交流各种信息,进行网上贸易等。
因此,信息的
安全与保密显得越来越重要。
信息的安全与保密不仅与国家的政治、军事和外交等有重大的关系,而且与国家的经济、商务活动以及个人都有极大的关系。
随着信息化社会的到来,数字信息与网络已成为人们生活中的重要组成部分,他们给我们带来方便的同时,也给我们带来了隐患:敏感信息可能轻易地被窃取、篡改、非法复制和传播等。
因此信息安全已成为人们关心的焦点,也是当今的研究热点和难点。
多媒体数据,尤其是图像,比传统的文字蕴涵更大的信息量,因而成为人类社会在信息利用方面的重要手段。
因此针对多媒体信息安全保护技术的研究也显得尤为重要,多媒体信息安全是集数学、密码学、信息论、概率论、计算复杂度理论和计算机网络以及其它计算机应用技术于一体的多学科交叉的研究课题。
三、设计内容
使用混沌序列图像加密技术对图像进行处理使加密后的图像
四、开发环境
MATLAB® & Simulink® Release 2010a windows7环境
五、分析设计
1.实验要求
使用matlab将图像信息隐藏,实现信息加密。
2.设计原理
运用异或运算将数据进行隐藏,连续使用同一数据对图像数据两次异或运算图像的数据不发生改变,利用这一特性对图像信息进行加密保
护。
用户输入的密码必须在0~1之间任何一个数据进行加密,并且加密
的程序与解密的程序输入的密码必须一致才能正确解密。
3.涉及到的程序代码
加密程序代码如下:
clear;clc;
x=imread('','bmp'); %读取图像信息
[a b c]=size(x); %将图像的大小赋给a b c
N=a*b; %定义变量N并赋值
m(1)=input('请输入密钥: '); %用户输入加密密码
disp('加密中...'); %显示提示信息
for i=1:N-1 %进行N-1次循环
m(i+1)=4*m(i)-4*m(i)^2; %循环产生密码
end
m=mod(1000*m,256); %1000*m除以256的余数
m=uint8(m); %强制转换为无符号整型
n=1; %定义变量n
for i=1:a
for j=1:b
e(i,j)=bitxor(m(n),x(i,j)); %将图像信息藏在e(i,j)矩阵中进行异或运算
n=n+1;
end
end
imwrite(e,'加密后的','bmp'); %显示解密成功提示信息
disp('加密成功');
winopen('加密后的'); %显示加密后图片
解密程序代码:
clear;clc;
x=imread('加密后的','bmp'); %读取图像信息
[a b c]=size(x); %将加密后图像的大小赋给a b c
N=a*b;
m(1)=input('请输入密钥: '); %用户输入预设加密密码
disp('解密中');
for i=1:N-1 %进行N-1次循环
m(i+1)=4*m(i)-4*m(i)^2; %循环产生原密码
end
m=mod(1000*m,256);
m=uint8(m);
n=1;
for i=1:a
for j=1:b
e(i,j)=bitxor(m(n),x(i,j)); % m(n)xor(m(n)xor x(i,j))==x(i,j)不带进位加法半加运算
n=n+1;
end
end
imwrite(e,'解密后的','bmp'); %将解密的图像输出命名为
disp('解密成功'); %显示解密成功提示信息
winopen('解密后的'); %显示解密后图片
4.主要的思想
图像信息生动形象,它已成为人类表达信息的重要手段之一,网络上的图像数据很多是要求发送方和接受都要进行加密通信,信息的安全与保密显得尤为重要,因此我想运用异或运算将数据进行隐藏,连续使用同一数据对图像数据两次异或运算图像的数据不发生改变,利用这一特性对图像信息进行加密保护。
六、结果及分析
1.运行示例
加密前的原图如下所示:
加密后的图像如下图:
运行程序是输入的密码:
运行结果如下:
加密后图片如下:
解密后的图像如下图:
运行解密程序输入加密时的密码:
解密后的图片:
2.结果评估
由程序的运行结果来看,原图被加密后在显示出来,已经无法辨别其内容,实现了图像数据的隐藏,这种混沌序列方法对图像数据的加密是十分有用,实现了信息的保密,在网络传输中能够很好地保护图像数据不被第三方轻易获取其内容,实现数据的隐藏保护。
六、参考文献
[1] 闵连权.一种实用的图像加密算法[J].河南郑州:信息工程大学测绘学院.2005年10月
[2] 图像加密技术研究背景意义及现状[K]赵晓宇.图像加密技术及其安全性估计[D].浙江大学,
[4]廖晓峰,肖迪,陈勇,向涛.混沌密码学及其应用.北京:科学出版社,
[5]卢开澄.计算机密码学——计算机网络中的数据保密与安全(第二版).北京:清华大学出版社,1998,210~212
[6] 舒斯特.混沌学引论.成都:四川教育出版社,1994
[7]刘式达等.自然科学中的混沌和分形.北京:北京大学出版社,2003
[8]吕金虎等.混沌时间序列分析及其应用.武汉:武汉大学出版社,2002
[9]Rossler O equation for continuous chaos. A,1976,57:397-398
[10]Chen G,Ueta T,Y et another chaotic attractor .Int. Bifurcation and chaos,1999,9:1465-1466
[11]Hale J,Verduyn L to functional differential equations. New York:Springer,1993
[12]韦鹏程,张伟,杨华千.一种基于共轭混沌映射的图像加密算法.计算机科学,2006,11:237-240
[13]王永,杨德刚,韦鹏程,张伟,杨华千.一种基于复合离散混沌系统的对称图像加密算法.计算机科学,2006,33(12):86-90
[14]廖晓峰,张伟,韦鹏程,杨华千等.对一种基于混沌映射的对称图像加密算法的改进.计算机科学,2007,34(12):248-251
[15]Arto ,1990
[16]Man Young Rhce. Cryptography and Secure Book
[17] Jianliang Zhu, Hongchao Zhao. Five- Dimensional Chaotic System and Its Circuitry Implementation[C]. 2nd International Congress on Image and Signal Processing, TianJin, 2009: 4232 - 4236( EI)
[18]韩峰,唐驾时.一个五维受控混沌系统的动力学行为[J].动力学与控制学报, 2010, 8( 3) : 205 - 209
七、研究工作进度
(1)工作进程安排:
2月10日-2月28日:办理毕业设计题目变更手续,阅读文献,收集资料,确立初步设计方案,完成开题报告。
3月1日-3月31日:完成设计方案,撰写论文初稿。
4月1日-4月30日:完成毕业设计撰写论文,修改格式,打印论文。
5月1日-5月20日:指导教师进行检查评分,进行论文评阅、论文答辩。
(2)我目前的工作进度是:
○1确定了毕业设计的题目,初步讨论的设计方案的可行性及大致方法步骤。
○2阅读了相关的文献和资料,对图像加密技术有了进一步的认识,重点浏览了图像加密的原理和几种方法。
○3阅读资料,确定加密方法即基于混沌理论的密码技术加密算法体制。
○4撰写开题报告,完成开题报告。