浅谈动态交通分配的三种模型以及算法

路网设计与交通流优化的数学模型引言路网设计与交通流优化是现代交通科学的重要组成部分，旨在提高交通效率、减少交通拥堵和提高人民生活质量。

为实现这一目标，研究人员开发了各种数学模型，其中包括路网设计模型、交通流优化模型等。

本文将介绍路网设计与交通流优化的数学模型，以及它们在解决交通问题中的应用。

一、路网设计模型路网设计是指确定适当的路线和道路宽度，以满足城市不同使用需求的过程。

路网设计模型能够根据道路拓扑、人口分布、交通流和路况等因素构建数学模型，并通过模拟测试来评估不同设计方案的效果。

路网设计模型通常可以分为两类：基于Route Choice模型和基于Traffic Assignment模型。

1. 基于Route Choice的路网设计模型基于Route Choice的路网设计模型是在给定的网络拓扑和路口状态下，预测交通流和路线选择的影响。

此类模型通常采用离散选择模型，其中车辆通过车道选择路线，这些选择的决策是基于降低总通行成本的策略。

该模型涉及到一系列方法，如传统试验、广义线性模型和离散选择模型等。

2. 基于Traffic Assignment的路网设计模型基于Traffic Assignment的路网设计模型将交通流视为网络流，将道路分配为不同的流量，以便实现网络通量的最小化。

这些模型通常将交通流表示为基于重力模型的概率流模式，并将分派和选路视为应对时空响应的交互性问题。

该模型可以用于构建交通流分配表格和地理信息系统分析。

二、交通流优化模型交通流优化是指通过改善道路系统、车辆和交通管理等措施来提高交通效率和减少拥堵的方法。

交通流优化模型可以根据交通流量、交通流性质、交通管理等因素来构建数学模型，并提出相应的优化方案以实现交通流的最佳分配。

交通流优化模型通常包括以下几个方面：1. 基于最小路径算法的交通流优化模型基于最小路径算法的交通流优化模型主要是通过路径选择算法找到最佳的路径，以最大程度地减小交通阻碍和拥堵问题。

交通规划中的交通拥堵模型交通拥堵是当今社会中一个普遍存在的问题。

为了有效解决交通拥堵问题，交通规划师常常使用各种模型来预测和管理交通拥堵。

本文将探讨交通规划中的交通拥堵模型，并介绍其中的一些常见方法。

交通拥堵模型是一种用于描述交通流量和交通拥堵程度之间关系的数学模型。

这些模型基于交通流量理论和交通工程原则，通过分析道路网络结构、车辆流动规律和交通需求来预测拥堵情况。

下面将介绍几种常见的交通拥堵模型。

一、流量密度模型流量密度模型是交通规划中最常用的一种模型。

该模型基于交通流量和道路面积之间的关系，通过测量车辆通过道路上的单位面积的数量，来评估交通拥堵的程度。

流量密度模型常用的评价指标有交通流量、通行速度和通行能力等。

交通规划师可以根据该模型的结果，制定相应措施来缓解交通拥堵。

二、交通模拟模型交通模拟模型是一种通过计算机模拟交通流动过程的方法。

该模型基于交通流理论和运动学原理，通过模拟车辆在道路上的运动轨迹，来预测交通拥堵的情况。

交通模拟模型可以考虑诸如交通信号灯、车辆行为和道路结构等因素，能够更加准确地模拟真实交通情况，提供更为精确的拥堵预测。

三、多目标优化模型多目标优化模型是一种通过优化算法解决交通拥堵问题的方法。

该模型通过设定目标函数和约束条件，将交通拥堵的影响因素进行量化，并根据优化算法的结果，找到最优的交通规划方案。

多目标优化模型通常考虑交通流量、通行时间、交通安全等多个指标，能够综合考虑各种因素，为交通规划提供全面的参考。

除了以上几种常见的交通拥堵模型，还有一些其他模型也在交通规划中得到应用，如网络模型、统计模型和人工神经网络模型等。

这些模型各有特点，可根据实际情况选择适合的模型进行应用。

然而，虽然交通拥堵模型能够为交通规划提供一定的指导，但是仍存在一些局限性。

首先，模型的精确性受限于输入数据的准确性和实际情况的变动性。

其次，模型无法完全考虑人们的行为心理因素和突发事件对交通拥堵的影响。

交通路网优化中的路径规划算法综述交通拥堵是大城市面临的一个重要挑战。

为了缓解交通拥堵问题，提高交通效率，路径规划算法在交通路网优化中起着重要的作用。

本文将综述目前常用的路径规划算法，包括Dijkstra算法、A*算法、Bellman-Ford算法和Floyd-Warshall算法，并分析其优缺点及应用场景。

1. Dijkstra算法Dijkstra算法是一种求解单源最短路径的经典算法。

它的基本思想是从起点开始，逐步扩展搜索范围，直到找到最短路径。

Dijkstra算法通过维护一个优先队列来选择当前距离起点最近的节点进行扩展，直到找到目标节点或搜索完所有节点。

该算法适用于无向图或有向图中有正权边的情况。

Dijkstra算法的时间复杂度为O((V + E) log V)，其中V是节点数，E是边数。

2. A*算法A*算法是一种启发式搜索算法，结合了Dijkstra算法和贪心算法的思想。

它引入了启发函数来指导搜索方向，以减少搜索空间。

在A*算法中，每个节点都有一个估计值，表示该节点到目标节点的预计代价。

算法通过维护一个优先队列来选择当前估计代价最小的节点进行扩展，直到找到目标节点。

A*算法的时间复杂度与Dijkstra算法相同，但在实际应用中通常具有更好的性能。

3. Bellman-Ford算法Bellman-Ford算法是一种求解单源最短路径的动态规划算法。

它通过使用松弛操作来逐步更新节点的最短路径估计值，直到收敛为止。

Bellman-Ford算法适用于解决带有负权边的图中的单源最短路径问题，但要求没有负环路。

该算法的时间复杂度为O(VE)，其中V是节点数，E是边数。

4. Floyd-Warshall算法Floyd-Warshall算法是一种求解全源最短路径的动态规划算法。

它通过使用中间节点来逐步更新节点间的最短路径估计值，直到得到全局最短路径。

Floyd-Warshall算法适用于解决带有负权边的图中的全源最短路径问题，但要求没有负环路。

交通分配的方法在城市交通运输中，交通分配是指根据车辆、乘客和货物的需求，将交通资源合理地分配到道路、轨道、水路等不同的交通网络中的过程。

交通分配的方法有很多种，下面将介绍几种常用的交通分配方法。

1. 预测模型法预测模型法是一种基于交通需求预测模型的交通分配方法。

通过对交通需求进行预测，得到交通网络中各个节点的交通量分布情况，然后根据交通网络的拓扑结构和交通流动规律，将交通需求分配到各个路径或路段中。

这种方法能够较准确地预测交通流量的分布，从而合理地分配交通资源。

2. 等时旅行法等时旅行法是一种基于等时旅行成本的交通分配方法。

等时旅行成本是指从出发点到目的地所需要的平均时间，它包括交通拥堵、交通信号等因素对旅行时间的影响。

根据等时旅行成本的大小，将交通需求分配到不同的路径或路段中，使得整个交通网络的等时旅行成本最小化。

3. 随机过程法随机过程法是一种基于随机过程理论的交通分配方法。

随机过程是指一组随机变量随时间变化的过程，能够较好地描述交通流的随机性。

通过建立交通流的随机过程模型，将交通需求按照一定的概率分布进行分配，从而得到交通流量的分布情况。

4. 最小路径法最小路径法是一种基于最小路径选择原则的交通分配方法。

根据交通网络中各个路径的长度、拥堵情况等因素，选择出最短路径或最小阻抗路径，并将交通需求分配到这些路径中。

这种方法能够使得交通流量分布更加均衡，减少拥堵现象的发生。

5. 均衡分配法均衡分配法是一种基于交通均衡理论的交通分配方法。

交通均衡理论认为，交通系统中的交通流量和交通成本会通过一定的调整过程逐渐趋于均衡状态。

根据交通均衡理论的原理，将交通需求按照一定的规则进行分配，使得交通系统中的交通流量和交通成本达到均衡状态。

在实际的交通分配过程中，常常会综合运用上述多种方法，根据具体情况选择合适的方法进行交通分配。

交通分配的目标是合理利用交通资源，提高交通效率，减少交通拥堵，为市民提供更加便捷、快速的出行方式。

ATIS条件下动态交通分配的交叉规划模型摘要本文在带有路段能力限制的动态路网上分析了atis对出行者的出行行为的影响，并构造了一个交叉规划模型来描述atis条件下，带有路段能力限制的动态路网上的交通分配问题。

关键词路段能力限制atis交叉规划中图分类号：c913.32文献标识码： a 文章编号：1引言随着各国经济和人民生会水平的不断提高，汽车保有量大幅增加，交通运输业空前繁荣，同时也给城市交通带来了难以承受的负荷。

解决交通拥挤的直接办法是提高路网的通行能力，但无论哪个城市都存在可供修建道路的空间有限，建设资金筹措困难等问题。

因此要比较有效的解决城市交通拥挤问题不能单纯的依靠增加道路面积和长度，而要不断完善路网结构和加强交通现代化。

许多研究人员发现公路网络的利用效率不高，现有的交通网络还有较大的能力提高空间，只要向用户及时提供信息，诱导好交通流，减少不必要行驶，就可以提高网络的运行效率。

在这种背景下智能运输系统应运而生。

信息作用下的动态交通配流问题是智能交通系统的核心理论内容和关键技术。

许多学者在这方面已经提出了许多很有成效的理论。

但之前的研究大都是在假定路段没有能力限制的条件下进行的，即任何路段都能承载分配给它的所有流量。

事实上，这种非拥挤假设是不成立的。

并且随着国民经济的发展，交通拥挤也变得更加恶化，如果仍然引用非拥挤条件下的模型来为智能交通系统提供基础数据，其准确性和可靠性就可想而知了。

本文将出行者分为装备了先进的交通信息系统（atis）的出行者和未装备的出行者两类。

在智能交通系统中，atis提供历史数据和实时可供预测的交通信息，影响出行者的个人出行行为。

显然，装备atis和未装备atis的出行者对出行费用的理解程度是不同的，从而有不同的路径选择行为。

装备和未装备atis的出行者存在于同一交通网络中，共同构成网络的种种交通状态。

他们的路径选择行为是相互影响的，一方面受自身条件的约束，另一方面还会受对方行为人的的影响，表现在能力限制上。

城市交通流量控制的模型和方法城市交通流量控制是指通过合理规划和管理城市道路、交通设施以及交通组织，引导和控制城市交通流量，提高道路通行效率，缓解交通拥堵，保障交通安全，并提供便利和高效的交通服务。

为了实现城市交通流量的控制，需要建立相应的模型和采用合适的方法。

下面将介绍城市交通流量控制的模型和方法。

一、城市交通流量控制的模型1.微观模型：微观模型是研究交通流动过程中个体交通行为的模型，一般基于交通流动的物理过程和驾驶人的决策行为。

常用的微观模型包括车辆跟踪模型、驾驶人行为模型和交通流动模型等。

-车辆跟踪模型：通过跟踪和模拟单个车辆的运动轨迹，研究交通流动的物理过程，包括车辆之间的距离、速度、加速度等参数。

-驾驶人行为模型：研究驾驶人在交通流动过程中的决策行为，包括车辆的起步、加速、减速、变道、路口选择等行为模式。

-交通流动模型：通过模拟单个车辆的运动轨迹，并将其扩展到整个交通网络中，研究交通流的动态演化过程，包括交通流的密度、速度和流量等参数。

2.宏观模型：宏观模型是研究交通流动过程中整体交通状态变化的模型，一般基于交通流理论和运输规划。

常用的宏观模型包括交通分配模型、交通流模型和交通规划模型等。

-交通分配模型：研究交通流动在交通网络中的分配方式，以及每个路段上的交通流量分布。

常用的交通分配模型有重力模型、用户均衡模型和系统最优模型等。

- 交通流模型：通过建立交通流动的动态平衡方程，研究交通流随时间和空间的变化规律。

常用的交通流模型有LWR模型、Greenshields模型和Daganzo模型等。

-交通规划模型：通过对城市交通需求进行预测和分析，提出合理的交通规划方案，包括道路扩建、交通设施改造和交通组织优化等。

二、城市交通流量控制的方法1.交通信号灯优化：通过对交通信号灯的定时和协调进行优化，使得交通信号灯在不同方向的车辆流量分配更加合理。

常用的交通信号灯优化方法包括固定周期信号灯控制、半固定周期信号灯控制和自适应信号灯控制等。

道路交通网络中的交通流模型随着城市化进程的加快，道路交通拥堵问题日益突出。

为了更好地解决道路交通问题，需要深入研究道路交通网络中的交通流模型。

一、交通流理论交通流理论是描述道路交通运算过程的一门学科，主要研究交通流的特征、交通拥堵的原因以及拥堵时的交通流规律等。

交通流的特征主要包括流量、密度、速度、加速度等，交通拥堵的原因主要是路网系统的瓶颈，以及车辆之间的相互影响。

拥堵时的交通流规律包括瓶颈效应、排队理论等。

二、交通模型交通模型是指用数学方法描述道路交通运输系统的一种技术手段。

通过建立交通模型，可以更加准确地预测交通状况，为交通规划和交通管理提供有效的决策依据。

目前，常见的交通模型主要包括微观模型和宏观模型两种。

1.微观模型微观模型是指运用微观经济学理论和方法来描述道路交通运输系统的模型。

微观模型主要研究各种交通网络和交通运输行为中的细节问题，如车辆的起点和终点、车辆的行驶路线、车辆的速度等。

2.宏观模型宏观模型是指运用宏观经济学理论和方法来描述道路交通运输系统的模型。

宏观模型主要研究交通流的总体特征，如交通流量、速度、密度等。

三、交通流模型交通流模型是指描述道路交通流动情况的一种数学模型。

交通流模型可以帮助我们更加深入地了解交通流的规律，以及不同交通状况下的交通流变化情况。

目前，常见的交通流模型包括线性模型、广义线性模型、非参数模型、卡尔曼滤波模型等。

1.线性模型线性模型是指将交通流的属性表示为线性的关系式，通常采用回归分析来进行建模。

线性模型适用于交通流量较小、交通状况相对稳定的情况。

2.广义线性模型广义线性模型是指将交通流的属性表示为非线性的关系式，通常采用广义回归分析来进行建模。

广义线性模型适用于交通流量较大、交通状况较为复杂的情况。

3.非参数模型非参数模型是指对于交通流的特征没有先验假设，采用一种无需先验假设的方法进行建模。

非参数模型适用于交通流特征非常复杂、交通状况无规律的情况。

4.卡尔曼滤波模型卡尔曼滤波模型是指采用卡尔曼滤波算法对交通流进行建模，以估算未知变量的值。

数学模型在城市交通拥堵中的应用城市交通拥堵一直是我们生活中的一个普遍问题，给人们的出行带来了很多不便。

然而，通过数学模型的应用，我们可以更好地理解交通拥堵现象，并且找到解决的途径。

本文将从数学模型的角度来探讨城市交通拥堵，并介绍一些常用的数学模型在解决交通拥堵问题上的应用。

1. 流体动力学模型流体动力学模型是用来研究流体运动的数学模型，它可以被应用于城市交通拥堵的分析中。

将车辆看作是流体，在道路网络中进行运动，通过对流体动力学模型的建立，可以模拟车辆的流动情况，进而分析交通瓶颈的位置和产生拥堵的原因，为交通管理者提供决策依据。

2. 马尔可夫模型马尔可夫模型是一种用来研究状态转移的数学模型，它可以被应用于分析交通状态的变化。

在城市交通中，交通流量的变化具有一定的随机性和不确定性，通过建立马尔可夫模型，可以预测道路交通流量的变化趋势，并据此优化交通信号灯的配时，从而减少交通拥堵。

3. 神经网络模型神经网络模型是一种模拟人脑神经系统工作原理的数学模型，它可以被应用于交通流量预测和优化路径选择。

通过对大量历史交通数据的分析和学习，神经网络模型可以预测未来的交通状况，并根据预测结果为驾驶员提供最佳路径选择，从而避免拥堵。

4. 线性规划模型线性规划模型是一种优化问题的数学模型，它可以被应用于交通流量控制和路网优化。

通过建立线性规划模型，可以确定最佳的交通流量控制策略，通过调整路口交通信号灯的时长，合理分配路口通行权重，来优化整个道路网络的交通效率，降低交通拥堵的发生。

5. 混合整数规划模型混合整数规划模型是一种包含了整数变量的优化问题的数学模型，它可以被应用于交通系统的布局和规划。

通过建立混合整数规划模型，可以确定最佳的道路网布局和公共交通线路规划，从而缓解交通压力，减少交通拥堵。

综上所述，数学模型在城市交通拥堵中的应用是多方面的，它们可以帮助我们更好地理解交通拥堵问题，并为交通管理者提供决策支持和优化方案。

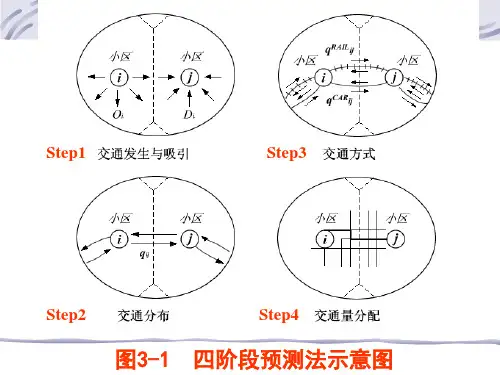
交通规划四阶段法模型TransCAD核心--交通规划模型TransCAD以交通规划“四阶段法”为基础，提供了完善的交通规划模型算法。

其中包括需求预测模型、公交模型、OD矩阵推算、路径模型、路网分析模型、物流模型等。

1(“四阶段法”交通规划模型? 出行产生/吸引模型交叉分类法:交叉分类法是根据一定的社会经济特点将一个城区的人口划分为若干类型。

然后，经验地估计每种类型的家庭或出行者的平均出行率，由此产生的出行率表，可用于预测该研究区的出行产生量。

回归分析模型:普遍采用两种回归分析模型。

第一种，使用以交通小区为标准的集计数据，将每个家庭的平均出行量作为因变量，小区特征属性的平均值作为说明变量(自变量)。

第二种，使用以单个的家庭或出行者为标准的非集计数据，以每个家庭或出行者的出行量作为因变量，家庭和出行者的特征属性作为说明变量(自变量)。

离散选择法: 离散选择法是使用非集计的家庭或单个出行者的数据估算它们的出行概率。

再将所得的结论集计起来即为预测的出行产生量。

? 产生/吸引平衡模型保持出行产生量不变:保持出行产生量不变，调整出行吸引量，使得吸引总量与产生总量相等。

保持出行吸引量不变:保持出行吸引量不变，调整出行产生量，使出行产生总量与吸引总量相等。

用户指定出行总量系数:同时调整出行产生量和出行吸引量，使产生量和吸引量之和等于出行总量乘以用户给定系数之积。

用户指定的出行总量:同时调整出行产生量和吸引量，使产生量和吸引量之和等于用户给定的值。

? 出行分布模型1增长系数法:是通过对现有的矩阵乘以系数实现的(增长系数由未来的出行产生量除以出行现状的产生量计算得出的)。

在无法获悉路网交通小区间距离、出行时间或综合费用等信息时，常常使用该方法。

——常增长系数法——出行产生受约束的增长系数法——出行吸引受约束的增长系数法——全约束增长系数(Fratar福来特法 )重力模型:主要的原理——两个地区之间的空间交流量与出行产生量/吸引量的乘积成正比，与两地之间的交通阻抗成反比。