高联难度几何题100道-打印整理版

高联班几何测试题（3）
命题人：万喜人
1、P为△ABC内一点，PD⊥BC于点D,PE⊥CA于点E,PF⊥AB于点F,K为直线PD上不同于P的一点,AK与BC交于点M,过点K作ST⊥AM交直线PE、PF分别于
点S、T.求证： u u=
2、△ABC形内的点E、F,使得∠ABE=∠CBF,∠ACE=∠BCF.直线AE、AF与△ABC的外接圆的第二个交点分别为M、N,分别交BC于点T、K.求证：（1）EM·FN=BM·CM;（2）ET·AN=AF·EM.
注：点E、F称为△ABC的等角共轭点，在另一点A处有一样的性
质∠BAE=∠CAF.
3、在△ABC中，D为边BC的中点，点E、F分别在直线CA、AB上，使得∠EDF=90°.求证：圆（AEF）、圆（E,EC）、圆（F,FB）三圆共点.
注:圆（AEF）表示过A、E、F三点的圆;圆（E,EC）表示以E为圆心，EC为半径的圆.
4、☉O中两弦AB=CD,分别过点C、D作☉O的切线，分别交直线AB于点E、F,△AEO、
△BFO的外心分别为O
1、O
2
.求证：O
1
O
2.
∥CD.
5、在△ABC中，AB=AC,O为外心，点D在直线BC上，☉A以A为圆心，AB为半径，☉D 以D圆心，DA为半径.求证：点O在☉A与☉D的根轴上.。

高联班几何测试题（11）时间：180 分钟命题人：万喜人11-1 在△ABC 中，点 D 、E 均在边 BC 上，BD=CE ，点 F 、G ，分别在 AB 、 AC 上，直线 FE 与 GD 交于点 K .FD 与 GE 交于点 V ，直线 AK 、AV 分别与 BC 交于点 L 、T .求证：B L =C T .证明 考虑△ACL 被直线 DKG 所截，由梅涅劳斯定理得!" ∙ $& ∙ '( = 1①#$ &' ()由△ABL 被直线 EKF 所截得,- ∙ )( ∙ '/= 1②.) (' /0式①×②，并利用 DC=BE 得!" ∙ $& ∙ '/ = 1③.) &' /0由△ACT 被直线 GEV 所截得23 ∙ '4 ∙ 6- = 1④&' 45 .$由△ABT 被直线 FDV 所截得78 ∙ 0# ∙54 = 1⑤/0 #5 4'式④×⑤，并利用 BD=EC 得6- ∙ $& ∙'/ = 1⑥#5 &' /0!"5.比较式③和⑥得.) = #5⟹ LD = TE ⟹ BL = CT.H11-2 已知△AB C 的外接圆⨀O ，∠BA C 的平分线交⨀O 于点D (D ≠ A)，过 B 、 C 两点的圆与边 CA 、AB 的第二个交点分别为 E 、F ，BE 与 CF 交于点 P ，过 A 、 E 、F 三点的圆与⨀O 交于点 A 、K ，DK 与 BC 交于点 T .求证：PT//AD .证明 如图，联结 FK 、BK 、EK 、CK ，AD 与 BE 交于点 V .因∠ABK=∠ACK， ∠AFK=∠AEK ⟹∠BFK=∠CEK， 则△BFK∽△CEK.又△BPF ∽△CPK ，由 AD 平分∠BA C 知 KD 平分∠BK C .A,6(0 0/ F0 所以，$5= ($= $.=F$G从而，PT 平分∠BPC，有∠BPT= HG ∠BPC.G又因∠BV D=∠BA C +∠AB V= (∠BA C +∠A BP +A C P )= H∠BPC所以，∠BPT=∠BVD，故 PT//AD.11-3 △ABC 的外接圆为⨀O ，点 D 在⨀O 上，点 E 、F 分别在 AB 、AC 上， ⨀O 中的弦 MN 使得 AD//EF//MN//BC.直线 AM 与 EF 交于点 P ，直线 DP 与⨀O 的第二个交点为 K.求证：E 、F 、N 、K 四点共圆.证明 如图（图形画得不相同时，证明过程类似），联结线段如图所示.因 AD//EF//BC ，则AC = BD 故∠BKP=∠ABC=∠BEP，从而 B 、K 、E 、P 四点共圆，∠PKE=∠PBE. 同理，∠PKF=∠PCF .所以，∠EKF=∠PKF -∠PKE=∠PCF=∠PBE . 因 EF//MN//BC ，则 BM = CN ，所以，∠PAE=∠CAN， ∠APE=∠AMN=∠CAN， 7- 于是，△APE∽△CAN，='F.'P'$结合∠EAN=∠PAC 得△AEN∽△APC， 故∠ENA=∠PCF .同理，△AFN∽△APB ⟹∠FNA=∠PBE.所 以 ，∠ENF=∠ENA -∠FNA=∠PCF -∠PBE=∠EKF， 故 E 、F 、N 、K 四点共圆.R= =11-4 圆Γ为△ABC 的外接圆，点 D 为BAC 的中点，点 E 、F 在直线 AD 上，使得 DE=DF ，点 E 、B 在线段 BC 的中垂线的同侧，ET ⊥AB 于点 T ，点 P 是点 T 关于 AB 的中点的对称点，FV ⊥AC 于点 V ，点 K 是点 V 关于 AC 的中点的对称点， EK 与 FP 交于点 N ，直线 DN 与圆Γ的第二个交点为 M.求证：P 、N 、K 、M 四点共圆.证明 首先证明 BT=CV.作 BX ⊥BC ，CY ⊥BC 交直线 AD 分别于点 X 、Y ，XR ⊥AB 于点 R ，YS ⊥AC 于点 S ，AH ⊥BC 于点 H.因 D 在 BC 的中垂线上，则 D 是 XY 的中点. 从而 EX=FY.XED又 XR//ET ，YS//FV ，Rt △AXR ∽Rt △AYS ， A YS则6R ='T='U=4S，NF.S'S'V/VP V故 TR=VS.,R ST 因 Rt △BXR ∽Rt △ABH ，则， TLKBHC'W0W M2XVU因 Rt △CYS ∽Rt △ACH ，则，,R 所以，$U'W$WST ∙ $WVU 0W 由 Rt △AXR ∽Rt △AYS ，，及 BX//AH//CY 得YR='S=0W.VU'V$W所以，BR=CS 从而 BT=CV.E DANFP V TKBC M=故AP=BT=CV=AK.因AD 是∠PAK 的外角的平分线，则AD//PK. 设DN 交PK 于点L，联结BL、BM.因D 为EF 的中点，则L 为PK 的中点.因Rt△AET∽Rt△KAL，则7- = '5 = F0，'( () F)结合∠EAK=∠BPL 得△AEK∽△PBL. 所以，∠AEN=∠PBL.又因为∠APK=∠DAB=∠DMB，则P、B、M、L 四点共圆，所以，∠PMN=∠PBL=∠AEK=∠PKN.故P、N、K、M 四点共圆.11-5△ABC 内接于⨀O，点P 是BC 的中点，点D、E 分别在射线PB、PC 上，使得PD=PE，⨀O的弦MN//BC，点M、B 在线段BC 的中垂线的同侧，点F、G 分别在直线AM、AN 上，且FD⊥BC，GE⊥BC，作FL⊥AC 于点L，GT⊥AB 于点T，DL 与ET 交于点K，求证：AK⊥BC.G证明如图（图形画得不相同时，证明过程类似）作AQ⊥BC 于点Q，设DL 交AQ 于点K G，ET 交AQ 于点K H，由梅涅劳斯定理得AL∙CD∙QK G= 1 =AT∙BE∙QK HLC DQ K G A TB EQ K H A因CD=BE，则要证AK⊥BC，只要证点K G、K H重合`(a`(b即证明(a'=(b'BZ=⟺AL ∙ EQ ∙ TB = 1 ①LC DQ AT延长 AO 交⨀O 于点 Z ，直线 BZ 与 AN 交于点 Y ，YV ⊥BC 于点 V ，直线 CZ 与 AM 交于点 X ，XU ⊥BC 于点 U.因 FL//XC （都与 AC 垂直），AQ//FD//XU ，7!'/ #` 则)$=/S=#d .6,&V .4 同理，'5='&=.`故式①⟺ "e ∙ .` #d #` ∙ .4= 1 .`⟺ DU = EV ⟺ CU = BV.2h因 Rt △CZJ ∽Rt △AZB ，则= ij ① '0 0i,hij 因 Rt △BZJ ∽Rt △AZC ，则②'$$i 因 MN//BC ，则∠BAY=∠CAX，7,0V则 Rt △ABY ∽Rt △ACX ，则'$= $S③①÷②，并利用式③得2h ∙ $S =$i⟹$j∙$S=0j∙0V0j 0V0i$i0i又 ZJ//XU ，则2h= $i ⟹ CU = $j∙$S $d $S $i同理BV =BJ∙BY于是，CU=BV ，证毕.高联班几何测试题（12）时间：180 分钟命题人：万喜人12-1 在△ABC 中，AB+AC=2BC ，P 为∠BAC 的角平分线上一点，PD ⊥BC 于点 D ，PE ⊥AC 于点 E ，PF ⊥AB 于点 F ，直线 DP 与 EF 交于点 K.求证：EK ∙ FK = 3PK H .AFKE PBC证明 如图，设 AP 与 BC 交于点 N. 因 AN 平分∠BAC A则7, = '$ = '0t'$ = 20P $P 0$因 PD ⊥BC ，PE ⊥AC ，PF ⊥AB ，FK 则 A 、E 、P 、F ，B 、D 、P 、F 分别四点共圆， E于是，∠PFK=∠PAE=∠NAB ， ∠FPK=∠B. P故△FPK ∽△ABN ， 所以v8 ='0= 2，即 PF=2PKBNDCF(0P又因 PF=PE ，由等腰三角形的性质得 PK H = PF H − EK ∙ FK ， 故EK ∙ FK = 3PK H .注：此题更一般的结论如下.在△ABC 中，N 是 BC 上一定点，P 是 AN 上的动点，PD ⊥BC 于点 D ，PE ⊥AC-y∙8y于点 E ，PF ⊥AB 于点 F ，直线 DP 与 EF 交于点 K ，则 F(b是一个定值，（这个定'P b值为）0P∙$P12-2 已知△ABC ，直线 d 、t 分别平分∠BAC 及其外角，点 D 在直线 d 上，直线 DB 与 t 交于点 E ，直线 DC 与 t 交于点 F ，作 MN//BC 交 AB 、AC 分别于点 M 、 N.直线 EM 与 FN 相交于点 K ，DK 与 BC 相交于点 P.求证：BP=PC.证明 如图，对△DEF 及点 K ，由角元塞瓦定理得z{| ∠G ∙ z{| ∠} ∙z{| ∠V=1①z{| ∠H z{| ∠~ z{| ∠Ät因 MN//BC 则AM = AN MB NCAE sin ∠ 5 AF sin ∠ 4 ⟹=BE sin ∠ 6CF sin ∠ 3⟹ sin ∠3 ∙ sin ∠5= AF ∙ BE ②sin ∠4 sin ∠6 CF AE又0. ∙$#=0# $/'. z{| ∠0'. '# z{| ∠0'# ∙ 7" z{| ∠$'# = '.'/ z{| ∠$'/'/⟹AF∙BE = BD③CF∙AE CD由式①、②、③得BD sin ∠ 1 = CD sin ∠ 2 ⟹ BP = PC .12-3 锐角△ABC 中，H 为垂心，过点 B 、C 的⨀P 交 CA 、AB 分别于点 D 、E ， BD 与 CE 交于点 F ，点 P 关于 BC 的对称点为 K.求证：FP//HK.PC.证明 如图，过 B 作 BT ⊥AB ，过 C 作 CT ⊥AC ，BT 与 CT 交于点 T ，联结 PB 、下面证明 F 、P 、T 三点共线因∠EBF = ∠DCF ，则∠FBT = ∠FCT 又∠PBT=90°-∠EBP=∠FCB ， ∠PCT=90°-∠DCP=∠FBC. 所以，F 、P 、T 三点共线 S △8,6 S △v,6 ⟺ S △826 =S △v26 BF ∙ BT sin ∠FBT⟺=CF ∙ CT sin ∠FCTBP ∙ BT sin ∠PBTCP ∙ CT sin ∠PCTBF sin ∠FCB ⟺ CF =sin ∠FBC 对△FBC ，由正弦定理得上式成立.故 F 、P 、T 三点共线.因 BT ⊥AB ， CH ⊥AB ，则 BT//CH. 同理，CT//BH.则四边形 BTCH 为平行四边形. 从而 HT 与 BC 互相平分， 又 PK 与 BC 互相垂直平分， 所以，HT 与 PK 互相平分.故 PT//HK ，即 FP//HK.=12-4 △ABC 内接于⨀O ，点 P 是 BC 的中点，点 D 、E 分别在射线 PB 、PC 上， 使得 PD=PE.⨀O 的弦 MN//BC ，点 M 、B 在线段 BC 的中垂线的同侧，点 F 、G 分别在直线 AM 、AN 上，且 FD ⊥BC ，GE ⊥BC.作 FT ⊥AB 于点 T ，GL ⊥AC 于点 L ， 直线 DT 、EL 交于点 K.求证：AK ⊥BC.G证明 如图（图形画得不相同时，证明过程类似）作 AQ ⊥BC 于点 Q ，设直线 DT 、EL 交 AQ 分别于点K G 、K H由梅涅劳斯定理得76 ∙ 0# ∙ `(a = 1 = ') ∙ $. ∙ `(b . 50 #` (a ')$ .` (b '要证 AK ⊥BC ，只要证点K G 、K H QK G K G A =QK H K H A因 BD=CE ，则只要证明76 ∙ .` ∙)$ = 1 ① 50 #` ')延长 AO 交⨀O 于点 Z ，ZB 交 AM 于点 X ，ZC 交 AN 于点 Y 作 XU ⊥BC 于点 U ，ZJ ⊥BC 于点 J ，YV ⊥BC 于点 V. 因 TF//BX ，AQ//FD//XU ，76'/#`则50=/S=#d，!2&V同理，= .4')'&.`故式①⟺DQ ∙EQ ∙EV = 1DU DQ EQ⟺ DU = EV ⟺ BU = CV.CZ= ==,ç0S 因 XU//ZJ ，则0j0i⟹ BU =同理，CV = CY∙CJ0S∙0j 0i,è 0j 因 Rt △BZJ ∽Rt △AZC ，则②'i'$2è$j 因 Rt △CZJ ∽Rt △AZB ，则③'i'0因 MN//BC ，则∠BAX=∠CAN7, 则 Rt △ABX ∽Rt △ACY ，则'$②÷③，并利用式④得 BZ = BJ ∙ AB = BJ ∙ BX0S$V④CZ CJ AC CJ CY⟹BX ∙ BJ = CY ∙ CJ .BZ CZ所以，BU=CV.证毕.=AMPQBE F CDK12-5 点 P 、Q 是△ABC 内部的等角共轭点，延长 AP 交△ABC 的外接圆圆Γ于点 D ，过点 P 、D 的一个圆交 BC 于点 E 、F ，直线 DE 、DF 与圆Γ的第二个交点分别为 M 、N.求证：M 、Q 、N 三点共线.N证明 如图，延长 AQ 交圆Γ于点 K ，联结线段如图所示. 因∠KBC=∠KAC=∠PAB则∠QBK=∠QBC+∠KBC=∠PBA+∠PAB=∠BPD 又∠BDP=∠BKQ 所以，△PBD ∽△BQK⟹PD = BD①BK KQ因∠DBE=∠DAC=∠BAK=∠BMK ， N∠BDE=∠BKM ， 则△BDE ∽△MKB ⟹DE = BD ②BK MKv" 式①÷式②得#.=í((`又因∠EDP=∠MKQ ， 所以，△DEP ∽△KQM ， 故∠DEP=∠KQM. 同理，∠DFP=∠KQN.所以，∠KQM+∠KQN=∠DEP+DFP=180°， 从而 M 、Q 、N 三点共线.AMQPB EFCD.。

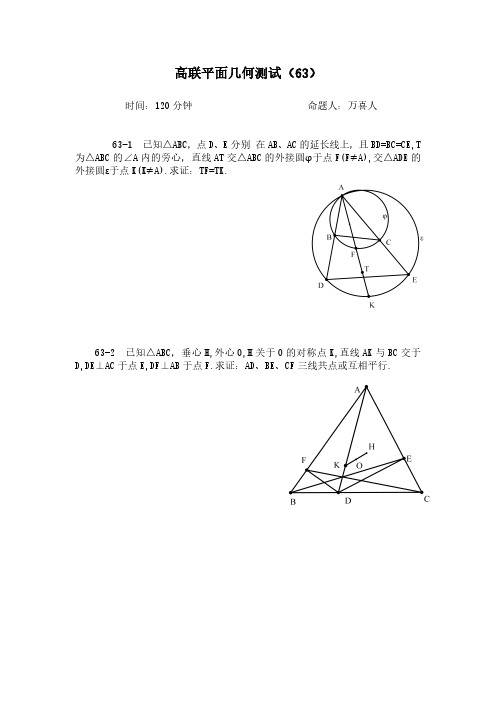
高联平面几何测试（63）
时间：120分钟命题人：万喜人
63-1已知△ABC，点D、E分别在AB、AC的延长线上，且BD=BC=CE,T 为△ABC的∠A内的旁心，直线AT交△ABC的外接圆φ于点F(F≠A),交△ADE的外接圆ε于点K(K≠A).求证：TF=TK.
63-2已知△ABC，垂心H,外心O,H关于O的对称点K,直线AK与BC交于D,DE⊥AC于点E,DF⊥AB于点F.求证：AD、BE、CF三线共点或互相平行.
63-3锐角△ABC中，AB≠AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点H.取点B关于AC的对称点T,点C关于AB的对称点V,M、N分别为BC、TV 的中点.MN与AH交于点K.求证：AK=KH.
63-4在△ABC中，P为BC的中点，点M、N分别在射线PB、PC上，PM=PN,点E、F满足∠BAE=∠CAF,EM⊥BC,FN⊥BC,作EU⊥AB于点U,FV⊥AC于点V,直线UM与VN交于点K.求证：AK⊥BC.
63-5在△ABC中，AB≠AC,点D、E、F分别在边BC、CA、AB上，AE=AF,AD、BE、CF三线共点于P,DT⊥EF于点T,TP与BC交于点N.△ABC的外接圆φ与△AEF 的外接圆ε交于点A、K,M为BC的中点.求证：直线AM与KN的交点在圆φ上.。

高联难度几何题100道
【实用版】
目录
1.几何题的重要性
2.高联难度几何题的特点
3.高联难度几何题的解决方法
4.高联难度几何题的训练价值
5.结语
正文
几何学作为数学的一个重要分支，其地位和作用不容忽视。

几何题在各种数学竞赛和考试中都占有重要地位，它能够锻炼学生的空间思维能力、逻辑推理能力和创新思维能力。

因此，对于学生来说，掌握几何题的解题技巧和方法是非常重要的。

高联难度几何题是几何题中难度较大的一部分，其特点是题目复杂、条件隐蔽、思路难以寻找。

这类题目的解决需要学生具有扎实的几何基础知识和丰富的解题经验，同时还需要具备敏锐的洞察力和创新思维能力。

解决高联难度几何题的方法有很多，其中最重要的方法是通过画图来帮助理解题目，找到解题思路。

此外，对于一些复杂的题目，还可以通过分割、旋转、翻转等方法来简化题目，找到解题的关键。

在解题过程中，还需要注意题目的条件和要求，避免出现低级错误。

高联难度几何题虽然难度较大，但是对于学生的数学能力和思维能力的提升具有很大的帮助。

通过解决这类题目，学生可以锻炼自己的空间思维能力和逻辑推理能力，同时也能够培养自己的创新思维和解决问题的能力。

总的来说，高联难度几何题虽然难度较大，但是对于学生的学习和发
展具有很大的帮助。

专题19 立体几何综合小题必刷100题任务一:善良模式(基础)1-30题一、单选题1．已知正四棱锥的底面边长和侧棱长均为2，则该正四棱锥的体积为（ ）A B ．C D ．2．已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列说法正确的是（ ） A ．若//m n ，n ⊂α，则//m αB ．若//m α，n ⊂α，则//m nC ．若m α⊂，n β⊂，//m n ，则//αβD ．若//αβ，m α⊂，则//m β3．如图，空间四边形OABC 中，点M 在线段OA 上，且2OM MA =，N 为BC 的中点，MN xOA yOB zOC =++，则x ，y ，z 的值分别为（ ）A ．12，23-，12B ．23-，12，12C ．12，12，23-D ．23，23，12-4．已知α，β，γ是三个不同的平面，m ，n 是两条不同的直线，下列命题为真命题的是（ ） A ．若//m α，//m β，则//αβB ．若//m α，//n α，则//m nC ．若m α⊥，n α⊥，则//m nD ．若αγ⊥，βγ⊥，则//αβ5．已知四棱锥P ABCD -的正视图和侧视图均为边长为2（单位：cm ）的正三角形，俯视图为正方形，则该四棱锥的体积（单位：3cm ）是（ ）A ．83BCD ．436．在正方体1111ABCD A B C D -中，则直线1A D 与直线AC 所成角大小为（ ）A ．30B ．45C ．60D ．907．正方体1111ABCD A B C D -的棱长为2，P 为侧面11ABB A 内动点，且满足1PD △PBC 面积的最小值为（ ）A ．1B C ．2 D ．2 8．在直三棱柱111ABC A B C -中，90ACB ∠=︒.1D 、1E 分别是11A B 、11A C 的中点，1CA CB CC ==，则1AE 与1BD 所成角的余弦值为（ ）A B C D9．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，则以下结论错误的是（ ）A ．BD ∥平面CB 1D 1 B ．AD ⊥平面CB 1D 1C ．AC 1⊥BDD ．异面直线AD 与CB 1所成的角为45°10．已知向量a ＝(2m ＋1，3，m －1)，b ＝(2，m ，－m )，且//a b ，则实数m 的值等于（ ）A ．32B ．－2C ．0D ．32或－2 11．正方体ABCD ­­A 1B 1C 1D 1中，E ，F 分别是线段BC ，CD 1的中点，则直线A 1B 与直线EF 的位置关系是（ ）A ．相交B ．异面C ．平行D ．垂直12．已知直三棱柱111ABC A B C -中，60ABC ∠=，2AB =，11BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为（ ）A B ．0 C D13．把一个皮球放入如图所示的由8根长均为20 cm 的铁丝接成的四棱锥形骨架内，使皮球的表面与8根铁丝都有接触点（皮球不变形），则皮球的半径为（ ）A ．cmB ．10 cmC ．cmD ．30 cm14．一种特殊的四面体叫做“鳖臑”，它的四个面均为直角三角形.如图，在四面体P -ABC 中，设E ，F 分别是PB ，PC 上的点，连接AE ，AF ，EF （此外不再增加任何连线），则图中直角三角形最多有（ ）A ．6个B ．8个C ．10个D ．12个15．在四棱锥P ABCD -中，底面是边长为4的正方形，且2,PA PB PD ===，则四棱锥外接球的表面积为（ ）A ．4πB ．8πC ．36πD ．144π二、多选题16．给出下列命题，其中正确的有（ ）A ．空间任意三个向量都可以作为一组基底B ．已知向量//a b ，则a 、b 与任何向量都不能构成空间的一组基底C ．已知空间向量(1,0,1)a =，(2,1,2)b =-，则//a bD ．已知空间向量(1,0,1)a =，(2,1,2)b =-，则向量a 在向量b 上的投影向量的坐标是848,,999⎛⎫- ⎪⎝⎭17．如图，正方体1111ABCD A B C D -的棱长为4，以下结论正确的是（ ）A ．直线1B D 与1BC 是异面直线B ．直线1A D 与1BC 平行C ．直线1BD 与1BD 垂直D ．三棱锥11A BC D -的体积为64318．如图，正方体1111ABCD A B C D -的棱长为1，点P 是棱1CC 上的一个动点（包含端点），则下列说法正确的是（ ）A ．存在点P ，使//DP 面11AB DB ．二面角1P BB D --的平面角大小为60︒C ．1PB PD +D ．P 到平面11AB D19．已知m 、n 是两条不同的直线，α、β、γ是三个不同的平面.下列说法中正确的是（ ） A ．若//m α，m β⊂，a n β⋂=，则//m n B ．若//m n ，//m α，则//n α C ．若a n β⋂=，αβ⊥，βγ⊥，则n γ⊥ D ．若m α⊥，m β⊥，//αγ，则//βγ20．在下列条件中，不能使M 与A ，B ，C 一定共面的是（ ）A ．OM ＝2OA －OB －OC ；B ．111532OM OA OB OC =++； C ．0MA MB MC ++=；D ．OM ＋OA ＋OB ＋OC ＝0；21．如图，在正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点．则满足MN OP ⊥的是（ ）A ．B ．C ．D ．22．设一空心球是在一个大球(称为外球)的内部挖去一个有相同球心的小球(称为内球)，已知内球面上的点与外球面上的点的最短距离为1，若某正方体的所有顶点均在外球面上､所有面均与内球相切，则（ ）A ．该正方体的核长为2B ．该正方体的体对角线长为3C 1D ．空心球的外球表面积为(12π+23．在正三棱柱111ABC A B C -中，1AB =，12AA =，1BC 与1B C 交于点F ，点E 是线段11A B 上的动点，则下列结论正确的是（ ）A ．1111222AF AB AC AA =++ B ．存在点E ，使得AF BE ⊥C ．三棱锥B AEF -D ．直线AF 与平面11BCC B第II 卷（非选择题）三、填空题24．已知正方体ABCD ­A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、BC 的中点，则三棱锥N ­DMC 1的体积为___________.25．已知正三棱锥的底面边长是6，侧棱与底面所成角为60︒，则此三棱锥的体积为__．26．如图，在直三棱柱111ABC A B C -中，∠ACB ＝90°，11AA AC BC ===，则异面直线1A B 与AC 所成角的余弦值是__________________．27．已知圆台上底半径为1，下底半径为3，高为2，则此圆台的外接球的表面积为______．28．如图，已知平行六面体1111ABCD A B C D -中，底面ABCD 是边长为2的正方形，侧棱1AA 长为3，且11120A AB A AD ∠=∠=︒，则1AC =__.29．如图，在空间四边形OABC 中，,,OA a OB b OC c ===，点M 在OA 上，且2OM MA =，N 为BC 的中点，则用向量,,a b c 表示向量MN =________．30．已知四棱锥P﹣ABCD的顶点都在球O的球面上，底面ABCD是边长为2的正方形，且P A⊥平面ABCD.若四棱锥P﹣ABCD的体积为163，则球O的表面积为___________.任务二:中立模式(中档)1-40题一、单选题1．在三棱锥P －ABC 中，3APB BPC CPA π∠∠∠===，△P AB ，△P AC ，△PBC 的面积分别记为123,,S S S ，且123322S S S === ）A BC D 2．在立体几何探究课上，老师给每个小组分发了一个正四面体的实物模型，同学们在探究的过程中得到了一些有趣的结论.已知直线//AD 平面α，直线//BC 平面α，F 是棱BC 上一动点，现有下列三个结论：⊥若,M N 分别为棱,AC BD 的中点，则直线//MN 平面α；⊥在棱BC 上存在点F ，使AF ⊥平面α；⊥当F 为棱BC 的中点时，平面ADF ⊥平面α.其中所有正确结论的编号是（ ）A ．⊥B ．⊥⊥C ．⊥⊥D ．⊥⊥3．已知圆台上底面半径为3，下底面半径为4，高为7，若点A 、B 、C 在下底面圆的圆周上，且AB BC ⊥，点Р在上底面圆的圆周上，则222PA PB PC ++的最小值为（ ）A ．246B ．226C ．208D ．1984．北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于2π与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和，例如：正四面体在每个顶点有3个面角，每个面角是π3，所以正四面体在各顶点的曲率为π2π3π3-⨯=，故其总曲率为4π，则四棱锥的总曲率为（ ）A ．2πB ．4πC ．5πD ．6π5．如图，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且EF A BEF -的体积为（ ）A ．112B ．14 C D ．不确定6．如图已知正方体1111ABCD A B C D -，点M 是对角线1AC 上的一点且1AM AC λ=，()0,1λ∈，则（）A ．当12λ=时，1AC ⊥平面1A DMB ．当12λ=时，//DM 平面11CB DC ．当1A DM 为直角三角形时，13λ=D ．当1A DM 的面积最小时，13λ=7．如图所示，已知空间四边形的每条边和对角线长都等于a ，点E 、F 、G 分别为AB 、AD 、DC 的中点，则a 2等于（ ）A ．2BA •ACB ．2AD •BDC ．2FG •CAD ．2EF •BC8．如图一，矩形ABCD 中，2BC AB =，AM BD ⊥交对角线BD 于点O ，交BC 于点M ．现将ABD △沿BD 翻折至A BD '的位置，如图二，点N 为棱A D '的中点，则下列判断一定成立的是（ ）A ．BD CN ⊥B ．AO '⊥平面BCDC ．//CN 平面A OM 'D ．平面A OM '⊥平面BCD9．点M 是棱长为3的正方体1111ABCD A B C D -中棱AB 的中点，12CN NC =，动点P 在正方形11AA D D （包括边界）内运动，且1//PB 平面DMN ，则PC 的长度范围为（ ）A ．B ．⎣C ．D ．⎣10．如图，在正方体1111ABCD A B C D -中，点M 在线段1BC (不包含端点)上运动，则下列判断中正确的是（ ）①1//A M 平面1ACD ； ②异面直线1A M 与1AD 所成角的取值范围是,32ππ⎛⎤⎥⎝⎦；③AC ⊥平面11MB D 恒成立； ④三棱锥1D AMC -的体积不是定值． A ．①③ B ．①② C ．①②③ D ．②④11．在四面体S ABC -中，SA ⊥平面ABC ，6BAC π∠=，SB =4,2SC SA ==，则该四面体的外接球的表面积是（ ）A ．253πB ．100πCD ．20π12．已知圆锥SO 的母线长为 ）A ．B ．24C ．36πD ．4813．如图，四棱锥P ABCD -的底面为矩形，PD ⊥底面ABCD ，1AD =，2PD AB ==，点E 是PB 的中点，过A ，D ，E 三点的平面α与平面PBC 的交线为l ，则下列结论中正确的有（ ）（1）//l 平面PAD ；（2）//AE 平面PCD ；（3）直线PA 与l （4）平面α截四棱锥P ABCD -所得的上、下两部分几何体的体积之比为35．A ．1个B ．2个C ．3个D ．4个14．在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，且PAD △是边长为2的正三角形，ABCD 是正方形，则四棱锥P ABCD -外接球的表面积为（ ）A ．293π B ．643π C ．263π D ．283π15．已知在正四面体ABCD 中，E 是AD 的中点，P 是棱AC 上的一动点，BP ＋PE 四面体内切球的体积为（ ）A B ．13πC ． D16．在棱长为2的正方体1111ABCD A B C D -中，点E ，F ，G ，H 分别为棱AB ，BC ，11C D ，11A D 的中点，若平面//α平面EFGH ，且平面α与棱11A B ，11B C ，1B B 分别交于点P ，Q ，S ，其中点Q 是棱11B C 的中点，则三棱锥1B PQS -的体积为（ ） A ．1B ．12C ．13D ．1617．已知球O ，过其球面上A ，B ，C 三点作截面，若点O 到该截面的距离是球半径的一半，且2AB BC ==，120B ∠=︒，则球O 的表面积为（ ）（注：球的表面积公式24)S r π=A ．643π B ．83πC ．323π D ．169π18．如图，在正三棱柱ABC ­A 1B 1C 1中，AC =CC 1，P 是A 1C 1的中点，则异面直线BC 与AP 所成角的余弦值为（ ）A ．0B ．13C D19．一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为1h 、2h 、3h ，则123::h h h =（ ）A．2B ． C 2:2 D 6:620．如图，二面角l αβ--的大小是60︒，线段AB α⊂．B l ∈，AB 与l 所成的角为30．直线AB 与平面β所成的角的正弦值是（ ）A B C D二、多选题21．如图，已知正方体1111ABCD A B C D -，则四个推断正确的是（ ）A ．111AC AD ⊥B ．11AC BD ⊥C ．平面11//A C B 平面1ACD D ．平面11A C B ⊥平面11BB D D22．正方体1111ABCD A B C D -的棱长为2，E ，F ，G 分别为11,,BC CC BB 的中点，则（ ）A ．直线1D D 与直线AF 垂直B ．直线1A G 与平面AEF 平行C ．平面AEF 截正方体所得的截面面积为92D ．点C 到平面AEF 的距离为2323．正四棱锥P ABCD -的所有棱长为2，用垂直于侧棱PC 的平面α截该四棱锥，则（ ） A ．截面可以是三角形B ．PA 与底面ABCD 所成的角为60︒C ．PA 与底面ABCD 所成的角为45︒D ．当平面α经过侧棱PC 中点时，截面分四棱锥得到的上下两部分几何体体积之比为3：124．如图，等腰直角三角形ABE 的斜边AB 为正四面体A BCD -的侧棱，2AB =，直角边AE 绕斜边AB 旋转一周，在旋转的过程中，下列说法正确的是（ ）A ．三棱锥E BCD -B ．三棱锥E BCD -C ．存在某个位置，使得AE BD ⊥D ．设二面角D ABE --的平面角为θ，且0θπ<<，则DAE θ<∠25．如图，在平行六面体1111ABCD A B C D -中，以顶点A 为端点的三条棱长均为6，且它们彼此的夹角都是60°，下列说法中不正确的是（ ）A ．1AC =B ．BD ⊥平面1ACCC ．向量1B C 与1AA 的夹角是60°D ．直线1BD 与AC26．正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 在侧面11CDD C 上运动，且满足1//B F 平面1A BE .以下命题正确的有（ ）A ．侧面11CDD C 上存在点F ，使得11B F CD ⊥ B ．直线1B F 与直线BC 所成角可能为60C ．平面1A BE 与平面11CDD C 所成锐二面角的正切值为D ．设正方体棱长为1，则过点E ，F ，A27．如图，边长为1的正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直，动点M ，N 分别在正方形对角线AC 和BF 上移动，且(0CM BN a a ==<<.则下列结论中正确的有（ ）A ．当12a =时，ME 与CN 相交 B ．MN 始终与平面BCE 平行 C ．异面直线AC 与BF 所成的角为45︒D ．当a =MN28．(多选)如图，ABCD ­A 1B 1C 1D 1为正方体，下面结论正确的是（ ）A ．BD ∥平面CB 1D 1 B ．AC 1⊥BD C ．AC 1⊥平面CB 1D 1D ．异面直线AD 与CB 1所成的角为60°29．已知四边形ABCD 为正方形，GD ⊥平面ABCD ，四边形DGEA 与四边形DGFC 也都为正方形，连接EF ，FB ，BE ，H 为BF 的中点，则下列结论正确的是（ ） A ．DE ⊥BFB ．EF 与CH 所成角为3π C ．EC ⊥平面DBFD ．BF 与平面ACFE 所成角为4π30．下图中正方体1111ABCD A B C D -边长为2，则下列说法正确的是（ ）A ．平面1C BD ⊥平面1A BDB ．正方体1111ABCD A BCD -外接球与正四面体11A DBCC ．正四面体11A DBCD ．四面体1A ADB第II 卷（非选择题）三、填空题31．空间四面体ABCD 中，2AB CD ==，3AD BC ==，BD =BD 和AC 所成的角为3π，则该四面体的外接球的表面积为 __.32．如图，A 、B 、C 、D 、P 是球O 上5个点，ABCD 为正方形，球心O 在平面ABCD 内，PB PD =，2PA PC =，则P A 与CD 所成角的余弦值为______．33．已知圆锥、圆柱的底面半径和体积都相等，则它们的轴截面的面积之比的比值是___________34．中国有悠久的金石文化，印信是金石文化的代表之一.下左图是南北朝官员独孤信的印信，它是由正方形和正三角形围成.右图是根据这只印信作出的直观图，直观图的所有顶点都在一正方体的表面上（如果一个正八边形的八个顶点都在这个正方体同一个侧面的四条棱上，那么这个八边形的边长就等于这个直观图的棱长）.__________.35．如图，在直三棱柱111ABC A B C -中，2BAC π∠=，11AB AC AA ===，已知G 与E 分别为11A B 和1CC 的中点，D 和F 分别为线段AC 和AB 上的动点（不包括端点），若GD EF ⊥，则线段DF 的长度的平方取值范围为__________.36．如图，在长方体1111ABCD A B C D -中，已知1AA =M ，N 分别在棱DA ，DC 上.二面角1D MN D --的大小为30°.若三棱锥1D DMN -，则三棱锥1D DMN -的外接球的表面积为___________.37．异面直线a 、b 所成角为3π，直线c 与a 、b 垂直且分别交于A 、B ，点C 、D 分别在直线a 、b 上，若1AC =，2AB =，3BD =，则CD =________．38．已知四棱锥S ﹣ABCD 的底面是边长为4的正方形，SD ⊥面ABCD ，点M 、N 分别是AD 、CD 的中点，P 为SD 上一点，且SD ＝3PD ＝3，H 为正方形ABCD 内一点，若SH ∥面PMN ，则SH 的最小值为__．39．如图，在ABC 中，AB AC ==1cos 3BAC ∠=-，D 是棱BC 的中点，以AD 为折痕把ACD △折叠，使点C 到达点C '的位置，则当三棱锥C ABD '-体积最大时，其外接球的表面积为___________.40．在如图所示的实验装置中，正方形框架的边长都是1，且平面ABCD ⊥平面ABEF ，活动弹子,M N 分别在正方形对角线,AC BF 上移动，若CM BN =，则MN 长度的最小值为__________．任务三:邪恶模式(困难)1-30题一、单选题1．已知四面体ABCD M ，N 分别为棱AD ，BC 的中点，F 为棱AB 上异于A ，B 的动点．有下列结论： ①线段MN 的长度为1；②若点G 为线段MN 上的动点，则无论点F 与G 如何运动，直线FG 与直线CD 都是异面直线；③MFN ∠的余弦值的取值范围为；④FMN 1． 其中正确结论的为（ ） A ．①② B ．②③C ．③④D ．①④2．已知三棱锥P ABC -，其中PA ⊥平面ABC ，2PA =，2AB AC ==，2BAC π∠=.已知点Q 为棱PA（不含端点）上的动点，若光线从点Q 出发，依次经过平面PBC 与平面ABC 反射后重新回到点Q ，则光线经过路径长度的取值范围为（ ）A ．(1B ．)4C ．4⎫⎪⎭D ．(3．如图，已知锐二面角l αβ--的大小为1θ，A α∈，B β∈，M l ∈，N l ∈，AM l ⊥，BN l ⊥，C ，D 为AB ，MN 的中点，若AM MN BN >>，记AN ，CD 与半平面β所成角分别为2θ，3θ，则（ ）A ．122θθ<，132θθ<B ．122θθ<，132θθ>C ．122θθ>，132θθ<D ．122θθ>，132θθ>4．在棱长为2的正方体1111ABCD A B C D -中，点M 是对角线1AC 上的点（点M 与1A C 、不重合），有以下四个结论：⊥存在点M ，使得平面1A DM ⊥平面1BC D ； ⊥存在点M ，使得//DM 平面11B D C ；⊥若1A DM 的周长为L ，则L⊥若1A DM 的面积为S ，则S ∈⎝． 则正确的结论为（ ） A ．⊥⊥ B ．⊥⊥⊥C ．⊥⊥⊥D ．⊥⊥5．在棱长为1的正方体1111ABCD A B C D -中，点P 是正方体棱上一点，若满足1PB PC d +=的点P 的个数为4，则d 的取值范围为（ ）A ．)2B ．C ．2,1⎡⎣D ．(16．在三棱锥D ABC -中，222AD AB AC BC ===，点A 在面BCD 上的投影G 是BCD △的垂心，二面角G AB C --的平面角记为α，二面角G BC A --的平面角记为β，二面角G CD A --的平面角记为γ，则（ ）A ．αβγ>>B ．αγβ>>C ．βγα>>D ．γβα>>7．已知正方体1111ABCD A B C D -的棱长为1，E 是1AA 的中点，F 是棱BC 上一点（不包括端点），则下列结论错误的是（ ）A ．三棱锥11CB EF -的体积为定值16B ．存在点F ，使得直线EF 与直线1CD 相交C ．当F 是棱BC 的中点时，直线EF 与直线1CD 所成的角为π6D ．平面1D EF 截正方体所得的截面是五边形8．如图，在等边三角形ABC 中，,D E 分别是线段,AB AC 上异于端点的动点，且BD CE =，现将三角形ADE 沿直线DE 折起，使平面ADE ⊥平面BCED ，当D 从B 滑动到A 的过程中，则下列选项中错误的是（ ）A ．ADB ∠的大小不会发生变化 B ．二面角A BDC --的平面角的大小不会发生变化 C ．BD 与平面ABC 所成的角变大 D ．AB 与DE 所成的角先变小后变大9．蹴鞠，又名“蹴球”“蹴圆”等，“蹴”有用脚蹴、踢的含义，“鞠”最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，类似今日的踢足球活动.如图所示，已知某“鞠”的表面上有四个点A ，B ，C ，D 满足10cm AB BC CD DA DB =====，15cm AC =，则该“鞠”的表面积为（ ）A ．2350cm 3πB ．2700cm 3πC ．2350cm πD 210．已知在Rt ABC △中，斜边2AB =，1BC =，若将Rt ABC △沿斜边AB 上的中线CD 折起，使平面ACD ⊥平面BCD ，则三棱锥A BCD -的外接球的表面积为（ ）A ．13π3B ．20π3C ．10π3 D ．7π311．如图，在长方体1111ABCD A B C D -中，3AB =，5AD =，14AA =，点F 是1AA 的中点，点E 为棱BC 上的动点，则平面1C EF 与平面11ABB A 所成的锐二面角正切的最小值是（ ）A ．513BC D ．13512．已知正方体1111ABCD A B C D -的棱长为M ，N 为体对角线1BD 的三等分点，动点P 在三角形1ACB内，且三角形PMN 的面积PMN S =△P 的轨迹长度为（ ）A B C D13．已知半球O 与圆台OO '有公共的底面，圆台上底面圆周在半球面上，半球的半径为1，则圆台侧面积取最大值时，圆台母线与底面所成角的余弦值为（ ）A B C D14．如图，等腰直角ABC 中，2AC BC ==，点P 为平面ABC 外一动点，满足PB AB =，2PBA π∠=，给出下列四个结论：①存在点P ，使得平面PAC ⊥平面PBC ； ②存在点P ，使得平面PAC ⊥平面PAB ； ③设PAC △的面积为S ，则S 的取值范围是(]0,4；④设二面角A PB C --的大小为α，则α的取值范围是π0,4⎛⎤⎥⎝⎦.其中正确结论是（ ） A ．①③ B ．①④C ．②③D ．②④15．已知AB 、CD 是圆O 的两条直径，且60AOC ∠=︒，如图1，沿AB 折起，使两个半圆面所在的平面垂直，折到点D 位置，如图2．设直线BD '与直线OC 所成的角为θ，则（ ）A ．90BD C '∠=︒且60θ>︒B ．90BDC '∠=︒且60θ≤︒ C ．90BD C '∠≠︒且60θ>︒ D ．90BD C '∠≠︒且60θ≤︒二、多选题16．如图，底面ABCD 为边长是4的正方形，半圆面APD ⊥底面ABCD ．点P 为半圆弧AD (不含A ，D 点)一动点．下列说法正确的是（ ）A ．三梭锥P —ABD 的每个侧面三角形都是直角三角形B ．三棱锥P —ABD 体积的最大值为83C ．三棱锥P —ABD 外接球的表面积为定值32πD ．直线PB 与平面ABCD17．已知正方体1111ABCD A B C D -的棱长为2，动点F 在正方形11CDD C 内，则（ ） A ．若112BF BC BD →→→⎛⎫=+ ⎪⎝⎭，则三棱锥的11-F B CC 的外接球表面积为4π B ．若1//B F 平面1A BD ，则1B F 不可能垂直1CD C ．若1C F ⊥平面1A CF ，则点F 的位置唯一D ．若点E 为BC 中点，则三棱锥11A AB E -的体积是三棱锥1-A FA B 体积的一半18．为弘扬中华民族优秀传统文化，某学校组织了《诵经典，获新知》的演讲比赛，本次比赛的冠军奖杯由一个铜球和一个托盘组成，如图⊥，已知球的体积为43π，托盘由边长为4的正三角形铜片沿各边中点的连线垂直向上折叠而成，如图⊥.则下列结论正确（ ）A ．经过三个顶点,,ABC 的球的截面圆的面积为4π B ．异面直线AD 与CF 所成的角的余弦值为58C ．多面体ABCDEF 的体积为94D ．球离球托底面DEF 119．已知边长为a 的菱形ABCD 中，3ADC π∠=，将ADC 沿AC 翻折，下列说法正确的是（ ）A ．在翻折的过程中，直线AD ，BC 始终不可能垂直B ．在翻折的过程中，三棱锥D ABC -体积最大值为38aC ．在翻折过程中，三棱锥D ABC -表面积最大时，其内切球表面积为2(14a π-D ．在翻折的过程中，点D 在面ABC 上的投影为D ，E 为棱CD 上的一个动点，ED '20．如图，ABC 是由具有公共直角边的两块直角三角板组成的三角形，4CAD π∠=，3BCD π∠=.现将Rt ACD △沿斜边AC 翻折成△11(D AC D 不在平面ABC 内）.若M ，N 分别为BC 和1BD 的中点，则在ACD △翻折过程中，下列结论正确的是（ ）A ．//MN 平面1ACDB ．1AD 与BC 不可能垂直C ．二面角1D AB C -- D ．直线1AD 与DM 所成角的取值范围为(,)63ππ21．已知边长为a 的菱形ABCD 中，π3ADC ∠=，将ADC 沿AC 翻折，下列说法正确的是（ ） A ．在翻折的过程中，直线AD ，BC 可能相互垂直B ．在翻折的过程中，三棱锥D ABC -体积最大值为38aC ．在翻折的过程中，三棱锥D ABC -表面积最大时，其内切球表面积为2(14a π-D ．在翻折的过程中，点D 在面ABC 上的投影为D ，E 为棱CD 上的一个动点，ED '22．已知正方体1111ABCD A B C D -的棱长为2，O 是底面ABCD 的中心，P 是棱11B C 上一点（不与端点重合），则（ ）A ．平面OCP 截正方体1111ABCD ABCD -所得截面一定是梯形 B ．存在点P ，使得三棱锥1P ABD -的体积为23C ．存在点P ，使得AP 与11CD 相交D ．当P 是棱11B C 的中点时，平面OCP 截正方体1111ABCD A B C D -外接球所得截面圆的面积269π23．在四面体ABCD 中，AB AC ⊥，AC CD ⊥，直线AB ，CD 所成的角为60°，AB CD ==，4AC =，则四面体ABCD 的外接球表面积为（ ）A B ．52π C ．80π D ．208π第II 卷（非选择题）三、填空题24θ，则当tan θ等于______时，侧面积最小．25．球面几何学是几何学的一个重要分支，在航海、航空、卫星定位等面都有广泛的应用，如图，A ，B ，C 是球面上不同的大圆（大圆是过球心的平面与球面的交线）上的三点，经过这三个点中任意两点的大圆的劣弧分别为,,AB BC CA ，由这三条劣弧围成的图形称为球面ABC ．已知地球半径为R ，北极为点N ，P ，Q 是地球表面上的两点若P ，Q 在赤道上，且PQ =，则球面NPQ △的面积为________；若NP PQ QN R ===，则球面NPQ △的面积为________．26．如图，在矩形ABCD 中，2,4,AB BC E ==是边AD 的中点，将ABE △沿直线BE 折成A BE ∠'，使得二面角A BE C '--的平面角为锐角，点F 在线段A B '上运动(包括端点)，当直线CF 与平面A BE '所成角最大时，FBE 在底面ABCD 内的射影面积为___________.27．已知三棱锥A BCD -的三条侧棱两两垂直，AB 与底面BCD 成30角，P 是平面BCD 内任意一点，则AP BP的最小值是________.28．已知正方体1111ABCD A B C D -的棱长为2，点E 是棱AD 的中点，点,F G 在平面1111D C B A 内，若EF =CE BG ⊥，则FG 的最小值为_________．29．在棱长为1的正方体1111ABCD A B C D -中，过对角线1BD 的一个平面交1AA 于E ，交1CC 于F ，得四边形1BFD E ，给出下列结论：①四边形1BFD E 有可能为梯形； ②四边形1BFD E 有可能为菱形； ③四边形1BFD E 在底面ABCD 内的投影一定是正方形； ④四边形1BFD E 有可能垂直于平面11BB D D ；⑤四边形1BFD E 其中正确结论的序号是_____________30．在棱长为4的正方体1111ABCD A B C D -中，E ，F 分别是BC 和11C D 的中点，经过点A ，E ，F 的平面把正方体1111ABCD A B C D -截成两部分，则截面的周长为________.。

高联班几何测试题（30）
时间：120分钟命题人：万喜人
30-1锐角△ABC中，AD、BE、CF分别为边BC、CA、AB上的高线，H是垂心，点P是不在直线BC上的任一点，HK⊥PB于点K，HT丄PC于点T，☉（AFK）与☉（AET）相交于点A、S.求证：D、K、S、T四点共圆.
30-2在△ABC中，∠BAC的平分线AD交BC于点D,延长CB至点E,使BE=AB,
过点E的一条直线交AD、AC分别于点F、K,直线BF、AC交于点T.求证: = 벨벨벨.
30-3圆内接四边形ABCD中，对角线AC与BD交于点E，边AD、BC延长后交于点F，CD与EF交于点P,点K在AB上,使得∠AFK=∠BFE,点M为AB的中点,FM 与PK交于点N.求证，PN=NK.
30-4圆Γ是ABC的外接圆，点M是BC的中点，延长AM交圆Γ于点D,点P 在边BC上，PE∥AB交AC于点E,PF∥AC交AB于点F,直线DP与圆Γ交于点D、K.求证:A、K、E、F四点共圆.
30-5☉O与☉Q相交于点A、B，☉O的弦AC交☉Q于点A、D，☉O的弦AE 交☉Q于点A、F，☉Q过D、F的切线交于点P，☉O过C、E的切线交于点K，直线AP交☉O于点A、M,AK交☉Q于点A、N,直线CK与DP交于点T,PF与KE交于点V.求证:B、N、P、M、K、T、V七点共圆.。

高联班几何测试题（54）
时间：120分钟命题人：万喜人
54-1在四边形ABCD中，△ABC、△ADC的垂心分别为H
1、H
2
,直线BH
1
与AD
交于点M,直线DH
2与CB于点N,MN与AC交于点P.求证：H
1
、P、H
2
三点共线.
54-2I为△ABC的内心，过B、C两点的圆交AB、AC分别于点D、E.F为AD的中点，J为△ADE的内心，直线FJ与DE交于点K,KP∥AB交直线AJ于点P.求证：I、P、C、E四点共圆.
54-3锐角△ABC内接于圆φ，点D、E、F、分别在边BC、CA、AB上，满足BF=DF,CE=DE,点M在圆φ上，满足AM⊥BC，直线MD交圆φ于点M、K，求证A、F、E、K四点共圆.
54-4延长☉O的直径AB至点P，过点P作一直线交☉O于点C、D（PC<PD）.作PE⊥AB于点E，PF⊥AB于点F，CF、DE与☉O的第二个交点分别于点M、N.求证：M、N、P三点共线.
54-5△ABC内接于圆Γ，P为△ABC内一点，P在边BC、CA、AB上的射影
、BAC 分别于点M、N,AM交直线EP、FP分别于T、分别为D、E、F.直线DP交BC
K.☉(ANT)与AB交于点A、U.☉（ANK）与AC交于点A、V.求证：UV∥BC。

高联班几何测试题（18）时间：120分钟命题人：万喜人的中点，点D关于BC的对称点为K,延18-1点D为△ABC的外接圆的弧 th长AB至E,使BE=AC,延长AC至点F,使CF=AB.求证：E、F、K三点共线.证明当AB=AC时，易知结论成立.当AB≠AC时，不妨设AB＜AC.如图，作平行四边形BACP.因BP=AC=BE,∠EBP=∠A,则∠BPE=90°- ∠A.同理，∠CPF=90°- ∠A.又∠BPC=∠A,所以，∠BPE+∠BPC+∠CPF=∠180°点P在直线EF上.且∠BPE=∠CPF,EF是∠BPC的外角平分线.作△BCP的外接圆交EF于点P、K/,联结BK/、CK/、BD、CD.则∠K/BC=∠CPF=90°- ∠A=∠BPE=∠K/CB.又∠DBC=∠DCB=90°- ∠A，所以，△K/BC≌△DBC.从而，点K/、D关于BC对称.故点K/与K重合.于是，E、F、K三点共线.注：类似命题在△ABC中，AB＜AC,延长AB至E,使BE=AC,在AC上取点F,（不含A）的中点，点使CF=AB,点D为△ABC的外接圆的弧 hD关于BC的对称点为K.求证：E、F、K三点共线.18-2已知△ABC，AB≠AC,∠BAC的平分线交△ABC的外接圆于D（D不同于A），点D关于BC的对称点K.点E、F分别在AB、AC上，使得BE=CF,BF与CE交于点P.求证：PK∥AD.证明如图，可设DK与BC互相垂直平分于点T,联结AT并延长至点S,使TS=TA,联结KS、PS、SC、SB.延长SB、CE使之交于点V.因TD=TK,TA=TS,则SK∥AD.因为四边形ABSC是平行四边形，则 h ㌰= 〸 ㌰=h뵸 ㌰=ht t㌰SP平分∠CSB.又因AD平分∠BAC由平行四边形ABSC的性质得SP∥AD.所以，S、P、K三点共线，且PK∥AD.18-3已知△ABC，AB≠AC,AD⊥BC于点D,作DE∥AC交AB于点E,EF∥BC交AD于点F,DK⊥BF于点K,M、N分别为BC、AD的中点.求证：D、M、K、N四点共圆.证明如图AB＞AC,联结KM、KN.因M、N分别为BC、AD的中点，则2DM=BD-CD,2FN=DF-AF.因DE∥AC,EF∥BC,则 体h体= 〸t〸=体뵸t뵸 体体뵸=h体t뵸= 体㔮h体体뵸㔮t뵸=体t뵸賀又因Rt△BDK≌Rt△DFK,则体㘹뵸㘹= 体体뵸=体t뵸賀.结合∠MDK=∠NFK得△DKM∽△FKN.∠DKM=∠FKN∠MKN=∠DKF=90°=∠NDC,故D、M、K、N四点共圆.18-4在△ABC中,O为外心,点D在边B C上，过点A作直线d⊥AD,作BE ⊥BC交d于点E,作CF⊥BC交d于点F,作EP⊥AB,FP⊥AC,EP与FP相交于点P.求证：点O为线段PD的中点.证明如图，设直线AD、d与△ABC的外接圆☉O的第二个交点分别为M、N.因d⊥AD,则MN为☉O的直径.设BE、CF与☉O的第二个交点分别为T、L,则四边形BCLT为矩形，BL为☉O的直径.=賀 .所以， t作NP/⊥EF交TL于点P/,联结TN、EP/.则E、T、P/、N四点共圆.故∠P/EN=∠P/TN=∠BAM.结合EA⊥AM知EP/⊥AB.同理FP/⊥AC,所以，点P/与P重合.联结BM、CN,作MK⊥BC于点K,KV∥BC交BE于点V.因∠PEF=∠BAM=∠MCB,同理∠PFE=∠MBC,所以，△PEF∽△MCB,PN、MK是对应边上的高，从而，t賀t㘹=〸뵸 h.因MD⊥EF由MK⊥BC,BC∥FV知MK⊥FV，则∠EFV=∠DMK.所以，Rt△FVE∽Rt△MKD,从而，t体t㘹=〸뵸뵸㌰=〸뵸 h.故PN=MD,且PN∥MD.注意到O为MN的中点得P、O、D三点共线，且点O为线段PD的中点.、 th 的中点，D为直线BC一点，18-5△ABC内接于☉O，M、N分别为 hDE∥AC交AB于点E,DF∥AB交AC于点F,ND与☉O的第二个交点为K,联结EF、AK,作KP⊥AK交AM于点P.求证：PD⊥EF.证明如图，不妨设AB＜AC(当AB=AC时，证明更容易).作△AKP的外接圆☉T,AB、AC的第二个交点分别为V、U,VU与BC交于点D/,AD与EF交于点X,联结线段如图所示.因∠AKP=90°，则T是AP的中点.的中点，则∠VAP=∠UAP,AV=AU.因M为 h考虑△ABC被直线VD/U所截，由梅涅劳斯定理得体 体 h·h t·t賀㌰ = ，体体 h=㌰ h .的中点，则KD平分∠BKC.因N为 th体体h=BK h㘹.因∠KVB=∠KUC，∠VBK=∠UCK,则△KVB∽△KUC.㌰ h = 㘹h㘹.故 体 体 h= 体体h D/与D重合，即V、D、U三点共线.所以，∠FDU=∠AVU=∠FUD.又四边形AEDF是平行四边形，于是，AE=DF=UF.又AT=UT,∠EAT=∠TAU=∠FUT.所以，△TAE≌△TUF TE=TF.注意X为EF的中点，得TX⊥EF.又TX为△APD的中位线，TX∥PD,所以，PD⊥EF.。